基于三点法的双曲线模型沉降预测与分析
双曲线法在沉降预测中的应用分析

且利用可记录个人习惯的评标助手, 自行查询、 搜索专业内的评
审环节及内容。需要询标时 由评 委提出问题 , 交给掌握投标人接
4 结语
、
随着国际化 全 球化 、 息化的发展趋势 , 信 电子招投标必将成 收文件 的网址或 邮箱及密钥 的人员统一加 密发送 , 统一接收 回复 为我国未来重要的招标方向 不仅是传统招投标理论在网络上的
、
程 中, 系统将评标过程记录备查。评标 报告等都 以电子数 据形式 毒 VP N等技术 ) 和智能评标 系统( 如建立 综合 联盟 专家库、 实现 存储 , 专家利用数字签名技术签名确认 。有条件 的重 大项 目甚至 异地在线评标【l 4 集成评 标数据库 的构建等许多难题 。展 5等)
,
电子文件交各有关评委判定 。c 实况评标 。专家利 用评标 电子 技术体现 更是一种 全新 的发 展观念 , ・ 即把思考问题 的出发 点和 助手 , 调取集成评标数据库中以往类似项 目招投标所形成的各种 思维方法都建立在适应 网络发展要求 之上 这就 为实现 、 善电 完
,
,
经济指标和参考数据 , 结合 自身 的专业经验进行评审 。在整个 过 子招投标提出了诸如网络及信 息安全技术( I S 防火墙 、 如 D 防病
.
.
评价情况 , 为他们增 减信用得分 。另外 , 过程 的预付 、 进度款 等 ,
Tak ng a o tt ed v l p ntte d o l i b u h e eo me r n fChi a’ lc r n c tn e i g a d b d i g n See to i e d rn n i d n
B 2 ] 目前 , 常用的计算最 终沉 降的方法 有 ]第一 类 , : 经典土力 学理 统法 ,P神经 网络法和遗传算法[ 。本文对常用 的预测方法进行 纹、 语音等) 自行登 录在 线评标 ; 于评标 的组 织 , 间和地点将 均将通过 网络在线操作 。最后 , 有电子记 录作 为项 目电子档案 对 时 所 发生重大的变化 , 一个评委 可以随时查看每 一份投标文件 , 每 而 资料的一部分 , 直接纳入项 目的建设资料中一并保存。
组合双曲线法在高铁路基沉降预测中的应用

组合双曲线法在高铁路基沉降预测中的应用李华东【摘要】高速铁路路堤普遍采用堆载土预压的施工方法加速路基的固结沉降.由于预压土荷载的快速施加,路基沉降曲线在填筑期与预压期之间常出现较为明显的变化.本文在总结和分析三点法、双曲线、指数曲线、泊松曲线、经验系数矫正法等路基沉降预测模型特点和适用性的基础上,基于传统双曲线沉降预测模型,提出一种适用于堆载预压工况下的高铁路基沉降预测方法——组合双曲线法.组合双曲线沉降预测模型考虑了堆载预压后沉降速率突然变大,将模型方程按照路基本体填筑期和堆载预压期分为两个阶段,分别进行参数确定.将组合双曲线沉降预测模型应用于京沈高铁某路基段,并与其他传统沉降预测模型计算结果进行对比,验证了组合双曲线法的适用性.【期刊名称】《铁道建筑技术》【年(卷),期】2019(000)004【总页数】5页(P138-141,146)【关键词】组合双曲线法;高速铁路;路基;沉降预测【作者】李华东【作者单位】中铁十六局集团第二工程有限公司天津 300162【正文语种】中文【中图分类】U213.1571 引言近年来中国在高铁建设上取得了举世瞩目的成就,从2008年我国第一条时速350 km京津城际开通运营,截至2018年我国高铁运营里程已达2.5万km。
中国国家发展改革委指出“十三五”期间全国铁路营业里程达到15万km,其中高速铁路3万km,可以看出高速铁路建设仍是重中之重。
高铁的高速性和舒适性依赖于线路的平顺性,而线下构筑物的变形量和稳定性是决定线路平顺的关键。
大量工程实践[1-5]表明铁路路基沉降变形问题是造成铁路运行事故的主要原因,而通过沉降预测判断路基沉降是否趋于稳定从而确定最佳铺轨时间是在施工阶段保证高铁服役期安全运行的重要手段。
高速铁路桥涵、隧道、路基的沉降预测方法有指数曲线、双曲线、泊松模型、灰色理论、三点法[6-7]等。
高铁路基施工过程主要包括填筑施工[8]和预压土堆载施工[9],在填筑完成进行堆载预压时,由于荷载施加较快易出现沉降速率突变,沉降曲线呈现较为明显的断层现象。
经验分析方法在软基沉降预测中的应用

= + 一t ( 、 L o 一 )
L, () o 6
5 0 10 0 gl0 5 2O O
笾
由式 ( ) 以得 出 t / s ( —t) 6可 — os一 0~ t 0 具有 线 性关 系 。当 t ∞ 时 , 一 最终沉 降量 为 :
图 3 X K 40断 面 5一P —t 线 图 L 0+ 5 曲
F g 3 s— P — t u v s o O +4 0 s cin i. r e fXL K c 5 e t o
从 图 I一 3可 知 : 在加 载 初期 , 降速 率较 大 , 沉 后期逐渐收敛 ; 随着荷 载施加加大, 沉降量呈现一
2o 0
日
∞—
警 一
() 3
10 5
10 0
根 据相关 资料 , 取 8叮 按下 式确定 : /T 。
卢 :l
筵5 0
0 5 0
其 中 : 和 为与 地基 的排水条 件 和地基 土性质 有
关 的参数。忽略瞬时沉降 的影响, 可以得到:
肖长生 王守 林 金 亮星 , ,
(. 1 深圳市岩土综合勘察设计有限公司, 广东 深圳 587 ; 11 2 2 .中南大学 土木工程学院, 湖南 长沙 4 ̄7 ) 13 5
摘 要 :结合 某填 海 造 地 道路 软 基 处 理 工程 实例 , 以软 基 沉 降 监 测 实测数 据 为 依 据 , 用双 曲 线 法 和 三 点 法 等 经 验 分 析 方 采
区别 。各 断 面用三 点 法 取不 同时 间 间 隔预 测 的 后
期 沉降拟 合 曲线 及 与 实 测 数 据 的 对 比如 图 4 6
图 1 P 1 0 断 面 s—P —t X K +10 曲线 图
沉降预测方法..
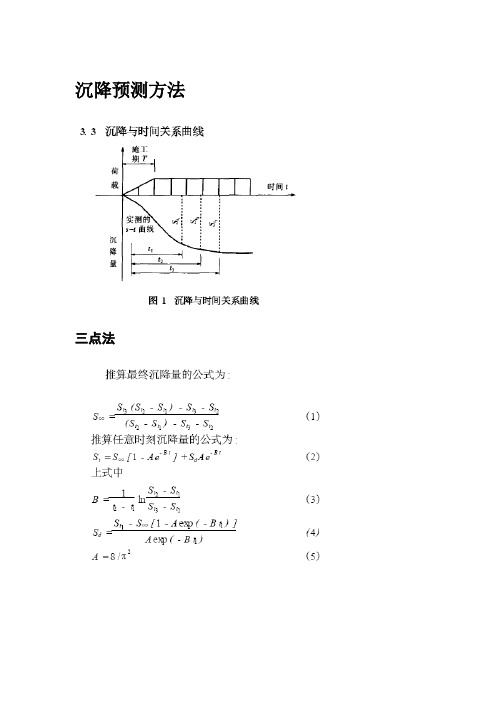
沉降预测方法三点法指数曲线法1指数曲线法2对数曲线法双曲线法3扩展双曲线法曲线拟合法工程中常用的拟合曲线有双曲线形式、指数形式、星野法和对数双曲线(三点法)形式等。
其中以三点法最简单,根据固结理论,只需要知道最大恒载时段内的3个等时间间隔内的沉降观测数据即可推算出最终沉降量和任意时刻的沉降量。
严格来说,三点法应该称为半经验公式,由于使用的数据量太少,因而不可避免地使所得结果较为粗糙,实际应用中也很少单独使用。
其他3种模型可以有效地提取出实测沉降序列的信息,特别是双曲线模型,由于可以方便地转化为对直线的最小二乘拟合,且拟合效果较好,待定参数少且其易于确定,表示的沉降发展规律与许多实际工程相符合,相对指数曲线模型和星野法模型更为简单易行,因此广泛应用于实际工程中。
双曲线法双曲线法假设路堤在进入预压期后实测沉降过程线按双曲线变化,其基本方程式如下[53]:()000t t b a t t S S t -+-+= (0-错误!未定义书签。
)式中,t S 为t 时刻的沉降量;0S 为预压期任意0t 时刻的沉降量;a 、b 为待定系数。
沉降量填土高度图 0-错误!未定义书签。
沉降预测示意图式7-1可变化为:()00t t b a S S t t t -+=-- (0-1)a 和b 分别为()()o t S S t t --/0~()o t t -关系图上的截距和斜率,其值可通过线性回归方程求出,也可用图解法直接求得,求得a 和b 后则可以预测今后任意时刻沉降量t S ,最终沉降量b S S /10+=∞ (0-错误!未定义书签。
)星野法日本的星野法[54]在京津唐高等级公路中曾有应用。
星野根据现场实测值证明了总沉降(包括剪切应变的沉降在内)是与时间的平方根成正比:()02001t t K t t AK S S t -+-+= (0-错误!未定义书签。
)式中,t S 、0S 分别为t 时刻对应的沉降量和假定的瞬时沉降量;0t 为假定瞬时沉降对应的时间;A,K 均为待定参数。
路基沉降计算及分析

107
2020.07 |
详见下式:
b
a s d t d s
=+1.9遗传算法
遗传算法是以自然进化论和遗传变异理论为根本的的新型计算方法。
设定研究事物为目标对象,假设函数为x 1,x 2,…,x n ∈Ω,F ∈R 。
通过计算目标函数的最小值,寻找所需的最优解。
具体详见下式:F (x )=f (x 1,x 2,…,x n )1.10泊松曲线法
泊松曲线法常用于模拟研究对象产生、成长、发展成熟,到达顶峰值的过程规律。
具体详见下式:b t
t a e c y −
+=
1
108|CHINA HOUSING FACILITIES
何泳超,(1985.5—),男,广东省中山市人,工学硕士,工程师,一级注册结构工程师,注册土木工程师(岩土),注册咨询工程师(投资),
稳
水
低
特
认
应
下,
政
政工程的关键建筑技术有很好的了解,真正提高了市政工程和城市建筑的质量,从而有效的提高我国市政工程建造的总体质量。
参考文献
[1]骆江红.市政道路工程施工安全管理问题与优化对策[J].黑龙江交通科技,2020,43(01):228-229.
[2]徐超.市政道路施工管理存在问题及解决对策探索[J].建材与装饰,2020(01):257-258.
[3]胡成建,胡奇鉴.市政道路桥梁工程施工管理中的问题与优化对策[J].中国设备工程,2019(20):180-182.
[4]胡如秋.市政道路工程施工组织与管理问题及解决对策研究[J].城市建设理论研究(电子版),2018(34):166.。
双曲线模型在沉降监测预报中的应用

法 , 模 型 不 仅 受 外 界 各 因 素 的影 响 , 受 时 间 因 Байду номын сангаас该 还
2 双 曲线 沉 降预 报模 型
通常利用沉降数据进行预报的方法有很 多, 曲 双 线模 型反应的是非线性关系 , 并且双曲线模 型编程简 单, 实用 。本文选取了双曲线模型进行某建筑物沉降
变形监测 中 常用 的模 型有 以下 几个 : 性 回归 线 法 、 间序 列 分析法 、 色系统 理论 、 时 灰 卡尔曼滤 波技 术、 人工神经 网络 、 小波 分析理论等 。下面针 对这些 常用的模型进行简单 的叙述 。 () 1 线性回归法 ( 多元线性 回归 ) 线性 回归法是 : 通过建立观测 的变形与影 响该 变形 的外 因之 间的数 学关系来进行 预测分析的 , 由于考虑了影响变形 的几 种主要 因素 , 以利用线性 回归法进行预报 , 所 一般 情
系数 。 式() 1 经变 换 可 以得 到
s一
=
式() 3
了 L ]】 瓦 ) ÷ 6 [ : 式 += jJ ( [ L ÷【 6 4
结论 。
卡尔曼滤波是通过 观测向量估计随时 间不 断变化 的 状态 的过程 , 在预报过程中不断预报 、 不断修正 , 是一 种状态估计 。 () 5 人工神经 网络 ( af i N u ̄ N to s 在 A i  ̄ er e r ) i c w k
1 变 形 监测数 据 处理 常用 模型
方程 。
() 4 卡尔曼滤波技术是 一种递 推式 滤波算法 , 可 以很好 的对 动态的观测数据进行处理 。在卡尔曼 滤
双曲线法在箱梁支架预压沉降观测中的应用
(收稿日期:2018-12-24)双曲线法在箱梁支架预压沉降观测中的应用冒生远(嘉盛建设集团有限公司㊀南京㊀210000)摘㊀要㊀对沉降观测中双曲线预测模型及原理进行介绍ꎬ尝试对G312㊁G346南京龙潭港至绕越高速公路段改扩建工程现浇箱梁支架预压沉降变形进行预测分析ꎬ实测数据与相对应的预测曲线吻合度较好ꎬ客观地反映了支架沉降的动态发展情况ꎬ可以有效地用于梁体预拱度调整ꎮ关键词㊀双曲线㊀沉降预测㊀支架沉降㊀应用分析㊀㊀近年来ꎬ随着经济的快速发展ꎬ城市人口迅速增长ꎬ而城市空间扩容相对有限ꎬ大中型城市的交通压力迅速增大ꎮ经过多年探索ꎬ我国已经认识到:解决城市交通问题的根本出路在于优先发展地上交通为骨干的城市公共交通系统[1]ꎮ高架桥以其运量大㊁速度快㊁安全等特点成为我国解决城市交通拥堵的新途径ꎮ高架桥主梁主要以现浇梁为主ꎬ在现浇梁施工中ꎬ支架预压是一个重要环节ꎬ它不仅可以消除支架及地基的非弹性变形ꎬ得到支架的弹性变形值作为施工预拱度的依据ꎬ还能测出地基沉降ꎬ为采用同类型的桥梁施工提供经验数据ꎮ因此ꎬ对支架预压进行有效的沉降观测及预测ꎬ具有重要的实际意义ꎮ本文根据G312㊁G346南京龙潭港至绕越高速公路段改扩建工程中G312高架主线桥第14联第2跨的支架预压沉降数据ꎬ通过使用双曲线模型进行沉降变形分析和预测ꎬ验证该方法在支架预压沉降分析中的准确性和参考性[2]ꎮ1㊀双曲线模型的原理及优势双曲线法是假定下沉平均速率以双曲线形式减少的经验推导法ꎬ从增加荷载开始到任意时间ꎬ双曲线法推算下沉模式如图1所示ꎬ待定参数α㊁β的求法如图2所示[3]ꎮ双曲线模型近似认为沉降变化量与观测周期成双曲线变化ꎬ这是一种经验型的拟合方法ꎬ其数学模型为S(t)=S0+t-t0α+β(t-t0)ꎬt=1ꎬ2ꎬ ꎬn.㊀(1)式中ꎬt0为时间零点ꎻt为观测周期ꎻα㊁β为待定参数ꎻS(t)为第t期的沉降观测预测值ꎻS0为t0时刻时刻的沉降实测值ꎮ基于支架专项施工方案ꎬ预压沉降观测每12h观测一次ꎬ所以设t0为12hꎮ图1㊀双曲线法推算下沉模式图2㊀待定参数α㊁β的求法待定参数可借助实测数组ꎬ利用最小二乘法求解[4]ꎮ双曲线模型编程简单㊁实用ꎬ且反应的是非线性关系ꎬ该模型在沉降预测方面具有良好的效果ꎮ2㊀支架沉降量的分析与预测根据G312高架主线桥现浇箱梁支架专项施工方案ꎬ为了取得支架预压过程中的沉降及变形数据ꎬ沿支架纵向每跨布设5个断面(墩中心㊁1/4跨㊁32«江苏交通科技»2019年第2期1/2跨㊁3/4跨)ꎬ在每个横向按底板左边㊁中心㊁右边线交叉点处设置3个沉降点ꎬ预压控制点位布置如图3所示ꎮ图3㊀预压控制点位布置满载后ꎬ连续3d沉降速率为1mm/d视为支架稳定ꎬ但是根据双曲线模型ꎬ完成3次观测后ꎬ即可对支架的最终沉降进行预测(三点法)ꎬ其预测公式为S¥=t1-t2t2St2-t1St1x㊀(2)式中ꎬSt为t时(修正后)的实测沉降量ꎻS¥为最终沉降量[5]ꎮ对G312高架主线桥第14联第2跨的沉降观测数据进行分析ꎬ沉降观测分析结果如表1所示ꎮ表1㊀沉降观测分析结果点名位置起始观测日期上次观测日期累计沉降量/mm预测最终沉降/mm相关系数10944Z141#墩左2017/6/262017/6/3013.4618.520.9610944Z241#墩中2017/6/262017/6/3013.5017.660.9910944Z341#墩右2017/6/262017/6/3014.9619.610.9510952Z11/4跨左2017/6/262017/6/308.8915.830.9510952Z21/4跨中2017/6/262017/6/3013.3116.640.9810952Z31/4跨右2017/6/262017/6/308.0814.790.9410959Z11/2跨左2017/6/262017/6/3012.0221.330.9710959Z21/2跨中2017/6/262017/6/3014.2325.160.9810959Z31/2跨右2017/6/262017/6/3014.8020.650.9310967Z13/4跨左2017/6/262017/6/3011.4918.990.9510967Z23/4跨中2017/6/262017/6/3014.3724.520.9910967Z33/4跨右2017/6/262017/6/3014.9522.040.9710974Z142#墩左2017/6/262017/6/3014.8021.670.9710974Z242#墩中2017/6/262017/6/3010.8321.470.9910974Z342#墩右2017/6/262017/6/3013.3119.480.95㊀㊀表1中点名的命名规则为 里程+Z+1(2㊁3) ꎮ其中ꎬ Z 为沉降点类型ꎬ 1(2㊁3) 表示沉降点在该断面上的位置ꎬ 1 为断面左侧㊁ 2 为断面中间㊁ 3 为断面右侧ꎬ如断面K10+959上的沉降观测点的命名分别为:10959Z1㊁10959Z2和10959Z3ꎮ以中线上的沉降观测点为例ꎬ经程序得出拟合曲线方程及相关参数如表2所示ꎬ测得的曲线图如图4~图6所示ꎮ表2㊀拟合曲线方程及相关参数表拟合方程测点参数t0S0αβ相关系数R预测最终沉降量/mm双曲线法St=S0+t-t0α+β(t-t0)10952Z2观测结束日0(t0时沉降)0.1397020.06008670.9816.6410959Z2观测结束日0(t0时沉降)0.2561180.03975010.9825.1610967Z2观测结束日0(t0时沉降)0.3342030.0407910.9724.5242 «江苏交通科技»2019年第2期图4㊀10952Z2沉降预测曲线图5㊀10959Z2沉降预测曲线图6㊀10967Z2沉降预测曲线根据预测出得到最终沉降量对梁体预拱度进行调整ꎬ箱梁混凝土浇筑完成后ꎬ对梁面高程进行观测ꎬ梁面高程对比如表3所示ꎮ根据表3可知ꎬ混凝土浇筑后ꎬ梁体的顶面实测高程和设计高程几乎没有差别ꎬ其差值控制在ʃ5mm以内ꎮ表3㊀梁面高程对比桩号偏距设计高程/m实测高程/mΔ/mm备注K10+949.365K10+954.365K10+959.365K10+964.366K10+969.366-1531.05331.0563.0031.35331.3552.0+1531.05331.051-2.0-1531.10331.1063.0031.40331.4052.0+1531.10331.102-1.0-1531.15331.1541.0031.45331.450-3.0+1531.15331.1552.0-1531.20331.2063.0031.50331.5041.0+1531.20331.202-1.0-1531.25331.250-3.0031.55331.549-4.0+1531.25331.2530.0 - 为左偏ꎻ 0 为中线ꎻ+ 为右偏ꎮ㊀㊀3㊀总结随着城市高架桥的大量使用ꎬ桥梁工程施工对支架沉降观测的要求越来越高ꎬ选择双曲线模型进行沉降变形分析ꎬ可对实测数据进行有效的分析预测ꎬ既能缩短沉降观测周期㊁加快施工进度ꎬ又能客观反映支架沉降的动态发展情况ꎬ为工程提供更好的安全保障ꎮ在工程实践中可知ꎬ双曲线模型除了可用于对路基沉降进行预测和分析外ꎬ其预测和分析的结果ꎬ也具有一定的准确性和参考性ꎮ参考文献[1]沈长江ꎬ朱良ꎬ徐锋等.三点法在高铁桥梁沉降变形预测中的改进[J].城市勘测ꎬ2014(4):152155.[2]魏汝龙.三维变形条件下的最终沉降量计算[J].水利水运科学研究ꎬ1979(2):5084.[3]姬庆峰.双曲线法在路基沉降变形预测中的应用分析[J].黑龙江交通科技ꎬ2010ꎬ33(4):17ꎬ19.[4]袁辉明ꎬ戴少平.双曲线法预测高速公路软基沉降[J].山西建筑ꎬ2010ꎬ36(30):292293ꎬ358.[5]马国亮ꎬ方宝君.基于沉降监测的预测模型的选取[J].矿山测量ꎬ2009(4):3840.52«江苏交通科技»2019年第2期。
地基沉降预测的几种简单方法
将三点代入上式,可求出未知参数。(α采用理论或经验值)
第二页
3抛物线法
公式是
S = a (lg t ) 2 + b lg t + c
做出S-lgt曲线即可求 出a、b、c
第二页
4指数曲线法
指数法方程式 S t = 1 − Ae − Bt S m 材料上说A、B的求法和双曲线法一致。 我感觉和三点法一致。
第二页
5沉降速率法
方程为 S ∞ = mS c 在恒载条件下沉降速率为 S t = AS c e − β t 通过lnSt和t的数据进行线性回归分析。 求出A、Sc、和 β Pt U t = 1 − αe − β t 又 S t = [(m − 1) P + U t ]Sc 0 可求得各级荷载的m。
第二页
通过这些方法在项目数据上的运用,了解 到得出的一些数据也有很大不确定性,还 有很多细节要处理。
第二页
谢谢大家 Thanks for your attention
地基沉降预测的几种简单方法
这五种方法包括: 1双曲线法 2固结度对数配合法 3பைடு நூலகம்物线法
4指数曲线法 5沉降速率法
第二页
1双曲线法
双曲线方程为St=S0+ a + bt Sf=S0+
t
1 b
第一个公式可变成
t = a +bt St - S0
可做出 值。
沉降预测方法..
沉降预测方法三点法指数曲线法1指数曲线法2对数曲线法双曲线法3扩展双曲线法曲线拟合法工程中常用的拟合曲线有双曲线形式、指数形式、星野法和对数双曲线(三点法)形式等。
其中以三点法最简单,根据固结理论,只需要知道最大恒载时段内的3个等时间间隔内的沉降观测数据即可推算出最终沉降量和任意时刻的沉降量。
严格来说,三点法应该称为半经验公式,由于使用的数据量太少,因而不可避免地使所得结果较为粗糙,实际应用中也很少单独使用。
其他3种模型可以有效地提取出实测沉降序列的信息,特别是双曲线模型,由于可以方便地转化为对直线的最小二乘拟合,且拟合效果较好,待定参数少且其易于确定,表示的沉降发展规律与许多实际工程相符合,相对指数曲线模型和星野法模型更为简单易行,因此广泛应用于实际工程中。
双曲线法双曲线法假设路堤在进入预压期后实测沉降过程线按双曲线变化,其基本方程式如下[53]:()000t t b a t t S S t -+-+= (0-1)式中,t S 为t 时刻的沉降量;0S 为预压期任意0t 时刻的沉降量;a 、b 为待定系数。
沉降量图 0-1 沉降预测示意图式7-1可变化为:()00t t b a S S t t t -+=-- (0-2)a 和b 分别为()()o t S S t t --/0~()o t t -关系图上的截距和斜率,其值可通过线性回归方程求出,也可用图解法直接求得,求得a 和b 后则可以预测今后任意时刻沉降量t S ,最终沉降量b S S /10+=∞ (0-3)星野法日本的星野法[54]在京津唐高等级公路中曾有应用。
星野根据现场实测值证明了总沉降(包括剪切应变的沉降在内)是与时间的平方根成正比:()02001t t K t t AK S S t -+-+= (0-4)式中,t S 、0S 分别为t 时刻对应的沉降量和假定的瞬时沉降量;0t 为假定瞬时沉降对应的时间;A ,K 均为待定参数。
填土高度沉降量图 0-2 S ~t 关系模式图上式可变形为:)(11)()(0222200t t A K A S S t t -+=-- (0-5)式中,()22/1K A 和2/1A 分别为()()20/o S S t t --~()o t t -关系图上直线的截距和斜率,系数A 和K 可以通过图解法求出。
基于三点法的双曲线模型沉降预测与分析
基于三点法的双曲线模型沉降预测与分析摘 要 地铁施工中的建筑物沉降监测控制是地铁施工中的重要问题之一,利用深圳地铁7号线7301-2标西丽站名典咖啡建筑物沉降数据,将三点法的基本思想引入到双曲线模型,建立了基于三点法的双曲线模型。
具体做法是:在实测沉降曲线上选取3个适当的点作为预测样本,代入双曲线模型进行预测并将沉降结果进行分析。
结果表明,当选取的三点在符合沉降趋势的情况下,基于双曲线模型的三点法的预测误差小,与实测数据吻合较好,对沉降预测问题提供了一定的参考。
关键词 双曲线法 三点法 沉降预测1 引 言近年来,随着中国经济社会的快速发展,城市人口迅速增长,而城市空间扩容相对有限,大中型城市的交通压力迅速增大。
经过多年探索,我国已经认识到:解决城市的交通问题的根本出路在于优先发展以轨道交通为骨干的城市公共交通系统。
地铁以其具有运量大、速度快、安全、准点、保护环境、节约能源和用地等特点成为我国解决城市交通拥堵的新途径。
但是由于地铁地下施工的特殊性,必然会对地铁线路附近地表及建筑物产生一定沉降影响,为保证施工安全和地表建筑正常安全使用,必须定期对地表建筑物进行沉降观测,掌握其变形规律,并正确预测其未来形变量,以便及时采取措施,确保建筑物及人员安全。
本文根据深圳地铁7号线7301-2标西丽站西侧名典咖啡建筑物的沉降数据,通过使用基于双曲线模型的三点法进行沉降变形分析和预测,证实了该方法在在建筑物沉降分析中具有一定的准确性和参考性。
2 基于三点法的双曲线模型的建立 2.1 双曲线模型的基本方程【1-2】为)(000t t t t S S t -+-+=βα (1)式中:S 0为t 0时刻的沉降量;S t 为t 时刻的沉降量;α、β均为待定参数。
将式(1)改写为:)(000t t S S t t t -+=--βα (2)由上式可知,α、β分别为)(00t t S S t t t ----关系图中的截距和斜率,用图解法可以求出;将求得的α、β值代入式(1),可得任意t 时刻的沉降量S t 以及最终沉降量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于三点法的双曲线模型沉降预测与分析摘 要 地铁施工中的建筑物沉降监测控制是地铁施工中的重要问题之一,利用深圳地铁7号线7301-2标西丽站名典咖啡建筑物沉降数据,将三点法的基本思想引入到双曲线模型,建立了基于三点法的双曲线模型。
具体做法是:在实测沉降曲线上选取3个适当的点作为预测样本,代入双曲线模型进行预测并将沉降结果进行分析。
结果表明,当选取的三点在符合沉降趋势的情况下,基于双曲线模型的三点法的预测误差小,与实测数据吻合较好,对沉降预测问题提供了一定的参考。
关键词 双曲线法 三点法 沉降预测1 引 言近年来,随着中国经济社会的快速发展,城市人口迅速增长,而城市空间扩容相对有限,大中型城市的交通压力迅速增大。
经过多年探索,我国已经认识到:解决城市的交通问题的根本出路在于优先发展以轨道交通为骨干的城市公共交通系统。
地铁以其具有运量大、速度快、安全、准点、保护环境、节约能源和用地等特点成为我国解决城市交通拥堵的新途径。
但是由于地铁地下施工的特殊性,必然会对地铁线路附近地表及建筑物产生一定沉降影响,为保证施工安全和地表建筑正常安全使用,必须定期对地表建筑物进行沉降观测,掌握其变形规律,并正确预测其未来形变量,以便及时采取措施,确保建筑物及人员安全。
本文根据深圳地铁7号线7301-2标西丽站西侧名典咖啡建筑物的沉降数据,通过使用基于双曲线模型的三点法进行沉降变形分析和预测,证实了该方法在在建筑物沉降分析中具有一定的准确性和参考性。
2 基于三点法的双曲线模型的建立 2.1 双曲线模型的基本方程【1-2】为)(000t t t t S S t -+-+=βα (1)式中:S 0为t 0时刻的沉降量;S t 为t 时刻的沉降量;α、β均为待定参数。
将式(1)改写为:)(000t t S S t t t -+=--βα (2)由上式可知,α、β分别为)(00t t S S t t t ----关系图中的截距和斜率,用图解法可以求出;将求得的α、β值代入式(1),可得任意t 时刻的沉降量S t 以及最终沉降量。
2.2 三点法三点法的基本表达式为t d t t e S e S S δδηη--∞+-=)1( (3)式中:S d 为瞬时沉降;S ∞为最终沉降量;η、δ均为实测数据经过曲线回归求得的系数。
从实测沉降 s-时间t 曲线(图1)上取3点:(t 1,S 1)、(t 2,S 2)、(t 3,S 3),并要求t 3-t 2 = t 2-t 1。
将上述三点分别代入式(3),联立可得231212ln 1S S S S t t ---=δ (4))()()()(2312232123S S S S S S S S S S S ------=∞(5)η取28π时,则可求得S d 值为)ex p()]ex p(1[111t t S S S δηδη----=∞∞(6)根据实测数据确定δ、S ∞和S d 后,可以利用式(3)计算任意时刻沉降量。
图1 基于三点法的双曲线模型取点示意图2.3 基于三点法的双曲线模型的沉降求解过程基于三点法的双曲线模型是将三点法的基本思想引入到传统的双曲线模型之中,在实测数据中选取三点:(t 1,S 1 )、(t 2,S 2)、(t 3,S 3),Δt=t 3-t 2=t 2-t 1,S 1、S 2 、S 3互不相等,假定t 1=t 0,然后把这三点代入双曲线基本方程:)(00t t S S t t t -+=--βα (7)可以得到:⎪⎪⎭⎪⎪⎬⎫-+=---+=--)()(131313121212t t S S t t t t S S t t βαβα (8) 联立可得⎪⎪⎭⎪⎪⎬⎫--------=------=))()(())(())(())()(())()((23121313121213231213121323t t S S S S S S t t S S t t t t S S S S t t t t S S βα (9) 将α、β的值代入式(1),可得)(111t t t t S S t -+-+=βα (10)计算可以得到任意时刻的沉降量,当t →∞时,可得最终沉降量为 )()())((2231212231S S S S S S S S S S -----+=∞ (11)3 工程实例计算名典咖啡屋位于深圳市南山区沙河西路与留仙大道交叉口地铁7号线西丽站南区基坑的西侧,最近点距离基坑(围护结构外边缘)18.8m ,此外咖啡屋西侧有深圳地铁5、7号联络线隧道,隧道顶距地面15.7m ,最近点水平距离名典咖啡25m ,咖啡屋基础为柱下独立基础。
建筑物下方地质情况为:①、地下4m 为素填土,主要成份为黏性土、混砂砾、局部含碎石、块石、硬塑,具有压缩性;②、地下4m-8.6m 为粉质黏土,局部为混砂、含有少量有机质,具有高压缩性。
③、地下8.6m-10.5m 为砂砾,较为密实,局部为黏性土。
虽然名典咖啡屋在沉降变化中,受到多个可知和不可知因素的影响,使其短时间沉降变化数据具有较大的随机性和不规律性,但是这一沉降过程,在总体时间和区域范围内呈现一定的变化规律。
通过对原始观测数据进行处理和选取,进行计算,可以显示其规律性,并对未来沉降进行预测。
现以名典咖啡建筑物DM2沉降观测点数据为例,表1为观测沉降数据,建立基于双曲线模型的三点法预测模型,并进行时间点位选取及预测结果分析,图2为名典咖啡时间沉降曲线图。
4 不同选点方式对预测结果的影响分析2014-6-1 23.4 532 2014-6-21 32.0 552 2014-6-2 24.1 533 2014-7-3 37.3 564 2014-6-3 23.6 534 2014-7-19 43.56 580 2014-6-4 23.2 535 2014-8-6 34.6 598 2014-6-5 22.9 536 2014-8-24 44.7 616 2014-6-6 24.4 537 2014-9-444.7 627 2014-6-724.3538图2 名典咖啡沉降曲线在名典咖啡沉降数据中选取具有不同时间特征的四组点,第一组三个点为(t 1, S 1)、(t 2, S 2)、(t 3, S 3):数据为观测段前部分数据,时间间隔22天,(490,18.5)、(512, 20.1) 、(534, 23.6),代入式(9)可得到α、β的值:⎪⎪⎭⎪⎪⎬⎫-=--------==------=23.0))()(())(())((87.18))()(())()((23121313121213231213121323t t S S S S S S t t S S t t t t S S S S t t t t S S βα 再将α、β的值代入式(10)可以得到)490(23.087.184905.18---+=t t S t 6.12)()())((2231212231=-----+=∞S S S S S S S S S S第二组数据为观测段整体段数据:(490 18.5)、(534, 23.6)、(578, 43.56),时间间隔44天,⎪⎪⎭⎪⎪⎬⎫-=--------==------=12.0))()(())(())((7.13))()(())()((23121313121213231213121323t t S S S S S S t t S S t t t t S S S S t t t t S S βα )490(12.05.184905.18---+=t t S t80.4)()())((2231212231=-----+=∞S S S S S S S S S S第三组选取整个观测段后部数据 (490,18.5)、(552, 32)、(614, 44.7),时间间隔62天。
⎪⎪⎭⎪⎪⎬⎫=--------==------=002.0))()(())(())((45.4))()(())()((23121313121213231213121323t t S S S S S S t t S S t t t t S S S S t t t t S S βα )490(002.045.44905.18-+-+=t t S t 13.447)()())((2231212231=-----+=∞S S S S S S S S S S第四组选取整个观测段后部数据 (548,29)、(564, 37.3)、(580, 43.56),时间间隔16天。
⎪⎪⎭⎪⎪⎬⎫=--------==------=02.0))()(())(())((66.1))()(())()((23121313121213231213121323t t S S S S S S t t S S t t t t S S S S t t t t S S βα )548(02.066.154829-+-+=t t S t 9.79)()())((2231212231=-----+=∞S S S S S S S S S S图3 第四组数据沉降曲线将不同选段点数据模型与原始数据进行对比,获得图3,通过图3,我们可以看到,不同的选段点所获得的模型沉降曲线具有巨大差异,由此我们可以获得以下结论:(1)第一组数据和第二组数据,在模型沉降中存在着突变点,这是由于不满足 S 3- S 2 < S 2- S 1模型条件造成的,同时也证明了三点法双曲线模型在一定程度上存在着预测不确定性。
(2)由第三组数据所获取的模型与原始数据具有较好的一致性,并且通过模型计算所获得的第614天以的数据与实际测量数据具有很高的吻合性,说明通过使用三点法模型进行沉降预测具有一定的实用性及科学性。
通过对比,我们发现第三组数据比第一组及第二组数据覆盖更多的测量时间段,其数据更能反映沉降的整体趋势。
(3)第四组数据主要选取的点位于整体时间段后部,通过对比我们发现,其后段数据与实际测量原始数据拟合程度很高,但是通过模型计算所得的前段数据与原始数据差异较大,说明选取的时间段的数据对于预测临近时间段附近的变化具有较高可靠性,特别是用于未来沉降预测时,其准确性较高,具有实用意义。
(4)通过以上对比实验,当我们在使用基于三点法的双曲线模型用于沉降预测时,所选取的数据应该具有反映整体沉降趋势的数据,并且尽量多使用最新测量获取的数据,这样才能使预测所获得的未来短时间内(1个或者多个时间间隔)沉降数据具有较高可靠性和准确性。
