比和比例(沪教版六年级第三章知识点)
小学六年级_比和比例知识点梳理(最新整理)
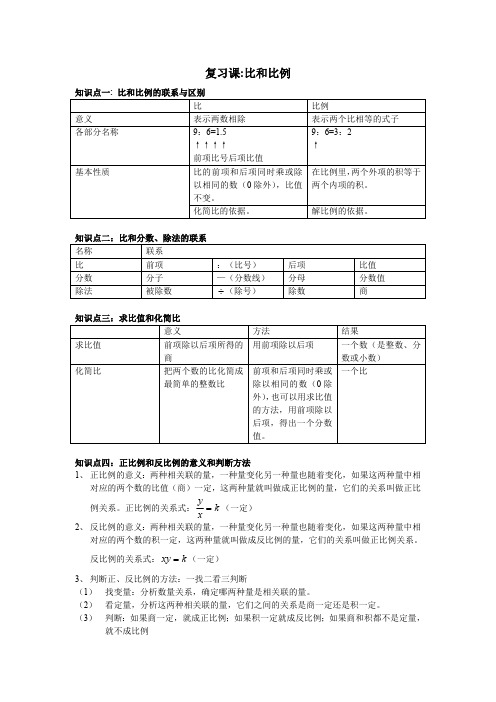
复习课:比和比例知识点一: 比和比例的联系与区别比比例意义表示两数相除表示两个比相等的式子各部分名称9:6=1.5↑↑↑↑前项比号后项比值9:6=3:2↑比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个外项的积等于两个内项的积。
基本性质化简比的依据。
解比例的依据。
知识点二:比和分数、除法的联系名称联系比前项:(比号)后项比值分数分子—(分数线)分母分数值除法被除数(除号)÷除数商知识点三:求比值和化简比意义方法结果求比值前项除以后项所得的商用前项除以后项一个数(是整数、分数或小数)化简比把两个数的比化简成最简单的整数比前项和后项同时乘或除以相同的数(0除外),也可以用求比值的方法,用前项除以后项,得出一个分数值。
一个比知识点四:正比例和反比例的意义和判断方法1、正比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的比值(商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
正比例的关系式:(一定)k xy=2、反比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做正比例关系。
反比例的关系式:(一定)k xy =3、判断正、反比例的方法:一找二看三判断(1)找变量:分析数量关系,确定哪两种量是相关联的量。
(2)看定量,分析这两种相关联的量,它们之间的关系是商一定还是积一定。
(3)判断:如果商一定,就成正比例;如果积一定就成反比例;如果商和积都不是定量,就不成比例4、正比例、反比例的区别与联系不同点名称意义不相同变化方向不相同关系式不同相同点正比例两种量中相对应的两个数的比值,也就是商一定一种量扩大(或缩小),另一种量也随之扩大(或缩小)。
(一定)k xy =反比例两种量中相对应的两个数的积一定一种量扩大(或缩小),另一种量也随之缩小(或扩大)。
(完整版)小学六年级_比和比例知识点梳理
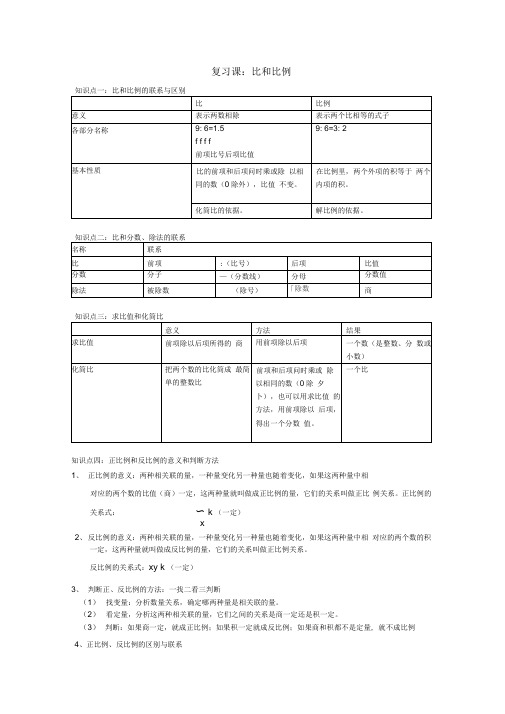
复习课:比和比例知识点四:正比例和反比例的意义和判断方法1、正比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的比值(商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
正比例的关系式:〜 k (一定)x2、反比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做正比例关系。
反比例的关系式:xy k (一定)3、判断正、反比例的方法:一找二看三判断(1)找变量:分析数量关系,确定哪两种量是相关联的量。
(2)看定量,分析这两种相关联的量,它们之间的关系是商一定还是积一定。
(3)判断:如果商一定,就成正比例;如果积一定就成反比例;如果商和积都不是定量, 就不成比例4、正比例、反比例的区别与联系知识点五:用比例知识解决问题1、按比例分配问题(1)按比例分配应用题:把一个量按照一定的比分配成几部分,求每个部分数量各是多少的应用题叫做按比例分配应用题。
(2)解题方法一般方法:把比转化成为分数,用分数方法解答,即先求出总分数,然后求出各部分量占总量的几分之几,最后按照求一个数的几分之几多少的解题方法,分别求出各部分的量是多少归一法:把比看做分得的分数,先求出各部分的总分数,然后再用“总量总份数=平均每份的量(归一)",再用"一份的量各部分量所对应的份数”,求出各部分的量。
用比例知识解答:首先设未知量为。
再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x的比例式,再解比例求出X。
2、用正、反比例知识解答应用题的步骤(1)分析数量关系。
判断成什么比例。
(2)找等量关系。
如果成正比例,则按等比找等量关系式;如果成反比例,则按等积找等量关系式。
(3)解比例式。
设未知数为X,并代入等量关系式,得正比例式或反比例式。
(4)解比例。
(5)检验并写出答语。
精讲典型题例题1填空(1)一项工程,甲单独做要4天,乙单独做要5天完成,甲和乙的工作效率比是(): ()(2)把2米:4厘米化成最简单的整数比是(),比值是()。
第三章比和比例知识点整理

第三章 比和比例 知识点整理1、比、分数和除法的表达式:比: 前项:后项 = 比值 分数:=分母分子分数值 除法:被除数÷除数 = 商2、求两个同类量的比值时,如果单位不同,先统一单位。
3、求比值的结果是不带单位的。
4、比值是一个数,它的形式可以是整数、分数,也可以是小数。
5、比的基本性质:比的前项和后项同时乘以或除以一个相同的数(0除外),比值不变。
分数的基本性质:分数的分子和分母同时乘以或除以一个相同的数(0除外),分数值不变。
除法的商不变性质:被除数和除数同时乘以或除以一个相同的数(0除外),商不变。
6、最简整数比:是指比的前项和后项都是整数,且它们互素。
7、化简比的结果还是一个比。
8、比有两种形式:比号形式和分数形式9、知三求一:即已知四个数能组成比例,求其中x 的值。
用内项积等于外项积、三个数分别与x 相乘等于另外两个数的乘积,列出三个不同的方程,解得三个答案。
若四个数成比例,如:2,3,4,x 成比例,则只有一种可能:2:3=4:x,直接列比例式即可。
10、把百分数化成最简分数,先将百分数写成分母是100的分数,再进行约分。
若不能直接进行约分,则先将分子分母利用分数的基本性质扩大相同的倍数后再进行约分。
11、小数化成百分数:添加百分号并将小数点往右移两位。
位数不够时用零补足。
12、百分数化成小数:去除百分号并将小数点往左移两位。
位数不够时用零补足。
13、分数化成百分数:一般把分数先化成小数,再把小数化成百分数。
14、分数化成小数,若除不尽,一般保留小数点后三位,即确保百分号前保留1位小数。
15、及格率=及格人数÷总人数成活率=成活棵树÷总棵树出勤率=实到人数÷应到人数,依此类推有合格率、优秀率等。
注:最后结果化成百分数形式。
16、盈亏问题:盈利率=成本盈利×100%=成本成本售价-×100% 亏损率=成本亏损×100%=成本售价成本-×100% 盈利=售价-成本=成本×盈利率注:一般要求成本时,将成本设为x ,再列方程求解。
03-第三章-比和比例-六年级(上)-知识点汇总-沪教版

第三章比和比例3.1比的意义1、将a与b相除叫a与b的比,记作a:b,读作a比b2、求a与b的比,b不能为零3、a叫做比例前项,b叫做比例后项,前项a除以后项b的商叫做比值4、求两个同类量的比值时,如果单位不同,先统一单位再做比5、比值可以用整数、分数或小数表示3.2 比的基本性质1、比的基本性质是比的前项和后项同时乘以或除以相同的数(0除外),比值不变2、利用比的基本性质,可以把比华为最简整数比3、两个数的比,可以用比号的形式表示,也可以用分数的形式表示4、三项连比性质是:如果a:b=m:n,b:c=n:k,那么a:b:c=m:n:k如果k≠0,那么a:b:c=ak:bk:ck=ak:bk:ck5、将三个整数比化为最简整数比,就是给每项除以最大公约数;将三个分数化为最简整数比,先求分母的最小公倍数,再给各项乘以分母的最小公倍数;将三个小数比化为最简整数比先给各项同乘以10,100,1000等,化为整数比,再化为最简整数比6、求三项连比的一般步骤是:(1)寻找关联量,求关联量对应的两个数的最小公倍数(2)根据毕的基本性质,把两个比中关联量化成相同的数(3)对应写出三项连比3.3 比例1、a(第一比例项):b(第二比例项)= c(第三比例项):d(第四比例项);其中a、d叫做比例外项,b、c叫做比例内项2、如果两个比例内项(外项)相同,即a:b=b:c,那么b叫做a、c的比例中项3、利用比例的基本性质,可以把比例方程转化化为我们常见的形式ad=bc,简单的说,就是内项之积等于外项之积4、列方程解应用题的一般书写步骤分四步:(1)设未知数(2)列方程(3)解方程(4)答5、列比例方程时,一定要注意对应关系,一定要注意同类量的单位要对应统一3.4 百分比的意义1、表示一个数是另一个数的百分之几的数叫做百分数,表示n %,读作百分之……2、把百分数化为小数3、 把小数化为百分数3.5 百分比的应用1、 三个关键词:是,占,的2、 一条主线:求部分占全体的百分数;3、 三类情景:一般文字题,统计图和统计表,恩格尔系数4、 赢利问题的两个基本公式: 售价-成本=赢利 赢利率=赢利/成本×100%;在售价、成本和赢利三个量中,只要知道其中的两个量,就可以计算出赢利率5、 打折问题的一个基本公式:原(售)价×折数=现(售)价;在原价、现价和折数三个量中,只要知道其中两个量,就可以计算出第三个量6、 亏损时赢利意义相对的量:赢利=售价-成本,亏损=成本-售价7、 银行利息的结算和本金、利率和期数有关(注意:贷款利息不纳税)利息=本金×利率×期数;利息税=利息×20%;税后本息和=本金+税后利息=本金+利息-利息税=本金+利息×(1-20%)增长率=增长的量/原来的基数×100%3.6 等可能事件1、 从实际生活中感悟那些事件是可能事件,哪些事件是不可能事件2、 可能性的大小可以用一个真分数或百分数表示第三章 比和比例(90分钟, 100分)一、 填空题 (每题3分,共36分)1.求比值:15∶151=. 2.求比值:0.2kg ∶120g=..3.化简:54∶65=. 4.化简:117∶78∶51=.5.2+0.25%= .6.已知:x ∶y =2∶3,y ∶z =6∶5,则x ∶y ∶z =.7.一幅地图,图上20厘米表示实际距离10千米,这幅地图的比例尺是8.某人看书,看了全书20%,还剩240页没看,这本书共有页.9.如果6a =5b,那么a :b=_____: ____.10.一件衣服打八折后便宜32元,这件衣服原价是元.11. 已知:,5135.7:=x 那么x = . 12. 12个型号相同的杯子,其中一等品有7个,二等品有3个,三等品有2个.从中任意取1个,取到二等品的可能性的大小是 .二、选择题 (3分×4=12分)13.下列各比中,能与12∶6组成比例的是 ( )(A )1∶2; (B )2∶1; (C )0.4∶2; (D )0.1∶0.5.14.把4.5、7.5、21 、 103这四个数组成比例,其内项的积是 ( ). (A )1.35 (B )3.75 (C )33.75 (D )2.2515.在一幅地图上,量得A 、B 两城市距离是7厘米,这幅地图的比例尺是1∶500000,那么A 、B 两城市之间的实际距离是 ( )(A )3.5千米 (B )150千米 (C )35千米 (D )350千米16.某商品打九折后,价格是a 元,则原价是 ( )(A )0.9a 元 (B )a (1-0.9)元 (C )9.0a 元 (D )9.01-a 元 三、化简连比(3分×3=9)17.已知x ∶y =2∶3,x ∶z =21∶32,求x ∶y ∶z 的最简整数比.18.解比例(1)x =54∶215 (2)x ∶∶153121=四、解答题(6分×6+7分=43分)19.飞机每小时飞行480千米,汽车每小时行驶60千米,飞机飞行214小时的路程,汽车要行使多少小时?(用解比例的方法)20.小红读一本书,第一天读完后,已读的和未读的页数比是1∶5,第二天又读了30页, 已读的和未读的页数比变为3∶5,问这本书有多少页?21.某工厂去年计划生产小轿车320辆,实际生产360辆,求该厂去年的增产率。
沪教版六年级预初-比和比例的意义及应用

基本内容 比和比例的意义及应用知识精要(一) 比的意义比的意义:a 、b 是两个数或两个同类的量,为了把b 和a 相比较,将a 和b 相除,叫做a 与b 的比。
记作b a :,或写成ba,其中0≠b ;读作a 比b ,或a 与b 的比。
(其中a 叫做比得前项,b 叫做比的后项。
前项a 除以后项b 所得的商叫做比值) 比的基本性质:比得前项和后项同时乘以或除以相同的数(0除外),比值不变。
三项连比的性质:(1) 如果n m b a ::=,k n c b ::=,那么k n m c b a ::::=。
(2) 如果0≠k ,那么kck b k a ck bk ak c b a ::::::==。
例1. 从学校到上海书城,甲走了12小时,乙走了36分钟,则甲与乙平均速度的比值是多少?例2. 已知4:3:=b a ,6:5:=c b ,求c b a ::例3. 某仓库储存有粮食225顿,已知大米:面粉:杂粮=1:4:10,求大米、面粉、杂粮各有多少吨?例4. 甲、乙、丙三人从昆山同坐一辆出租车回家。
当行到全程的52时,甲下了车;当行到全程的53时,乙下了车;丙到终点才下车。
他们三人共付车费290元。
甲、乙、丙三人按路程的远近各付款多少元?(二) 比例的意义(1)表示两个比相等的式子叫比例。
组成比例的四个数都不能是0。
(3)比例的基本性质:在比例中,两个内项的乘积,等于两个外项的乘积 例如:180∶3=240∶4 两个内项相乘:3×240=720 两个外项相乘:180×4=720这两个乘积有相等的关系,如果把比例写成分数形式,等号两端的分子和分母分别交叉相乘,积也有这种关系,(4)如何判断两个比能否成比例:根据比例的意义和性质可以判断两个比能否组成比例 例5. 已知6是4和x 的比例中项,求x例6. 一个比例的两个内项互为倒数,一个外项是81,另一个外项是( ) (5) 比例尺=图距:实际距离例7. 在比例尺是1:50000的地图上,A 、B 两地的图上距离是3厘米,那么A 、B 两地的实际距离是多少千米?例8. 将x 个物体按照:a b 的比例分配给甲、乙两个人,那么实际上甲、乙两个人各自分配到的物体数量与x 的比分别为():a a b +和():b a b +,所以甲分配到______个,乙分配到例9. 两个类别A、B,元素的数量比为:a b(这里a b),数量差为x,那么A的元素数量为______,B的元素数量为________拓展:例1. 已知甲、乙、丙三个数,甲的一半等于乙的2倍也等于丙的23,那么甲的23、乙的2倍、丙的一半,这三个数的比为多少?例2. 如下图所示,圆B与圆C的面积之和等于圆A面积的45,且圆A中的阴影部分面积占圆A面积的16,圆B的阴影部分面积占圆B面积的15,圆C的阴影部分面积占圆C面积的13.求圆A、圆B、圆C的面积之比.一、 填空题1. 2=()()183=2. 求比值,1.5小时:40分钟=3. 化成最简整数比,2:13:0.5= 4. 已知y x :=11:23,z y :=2:3,则z y x ::=5. 已知4:x =12:3,则x =_________6. 已知长方形的长和宽之比是4:3,长为16厘米,则宽为 厘米7. 已知8是23和x的比例中项,则x =____________ 8.25:36= :15 9. 已知x 是y 的_______,则x y :=5:210. 100米赛跑中小明用了14秒,小杰用了16秒,则小明与小杰的速度之比是__________11. 若a 的3倍是的b 的13,则a :b =________ 12. 若2:3=(4-x ):5,则x =_________13. 如果,235x y z x yz x+===-那么___________ 14. 若整数x 能与3、4、6这三个数组成比例,那么x =__________二、 选择题15. 将一个比的前项扩大2倍,后项缩小2倍后,这个比的比值与原比值相比( ) A.扩大了 B.缩小了 C.不变 D.无法确定 16. 下列四组数中,不能组成比例的是( ) A.2,3,4,6 B.1,2,2,4 C.0.1,0.3,0.5,1.5 D.1111,,,234517. 10克盐完全溶解在100克水中,则盐与盐水的重量比是( ) A.1:10 B.10:1 C.1:11 D.11:118. 若a :b=3:2,且b 2=ac ,则b :c=( )A.3:4B.2:3C.3:2D.4:319. 如图所示,阴影部分的面积占大圆面积的15,占小圆面积的13,则大、小圆面积之比是()A.5:3B.3:5C.3:2D.4:3三、简答题20. 已知35yx y=+,求x:y21. 已知x:y=1.5:1,y:z=25:36,求x:y:z四、解答题22. 在一张比例尺是1:6000000的地图上,量得上海到北京的距离是18厘米,那么上海到北京的实际距离是多少千米?23. 用比例方法求解:小明父亲工作3天可以得到450元,他工作一个月可以得到多少报酬?(一个月按22个工作日计)24. 用一根长120厘米的铁丝围成一个长方体(不计接头损耗)。
沪教版数学六年级上册 第三章《比和比例》 复习课件(共34张PPT)

2-0.9 2
-5
1 8 :x=0.5:16
综合练习
填空:
1)一个比例有两个( )项,两个( )项。
2)判断两个比是否能组成比例,可以看它们的(
)
也可以用(
进行判断。
3)写出比值是2.5的比,并组成比例(
)
4)在比例中,如果两个内项的分别是4和5,那么组成
两个外项的两个数的积一定是( )
5比)值甲是数(是乙数的1-)21 ,。甲数和乙数的比是(
3、一个筑路队修一条公路,原计划 每天修3.2千米,15天完成,实际每 天比原计划多修了25%,实际多少天 可以完成?(20)
学习检测
1)一个比例有两个( 内 )项,两个( 外 )项。 2)写出比值是2.5的比,并组成比例( 5:2=10:4 ) 3)在比例中,如果两个内项的分别是4和5,那么组成 两个外项的两个数的积一定是( 20)
你会吗?
化简下列各比并求比值:
3.6:1.4
2 —1 :0.8 7
1—81
:—4
5
500千克:2—21 吨 1米10厘米:15分米
你明白了吗?
—7 日 :12时 8
化简比是根据比的基本性质,把比的前项和后项都乘上或 者除以相同的数(0除外),求比值是根据比例的意义, 用前项除以后项。化简比的结果是一个前项和后项互质数 的整数比,而求比值的结果是一个数,可以是整数,也可 以是分数或者小数。
( ),周长的比是(
)。
A:1:3 B: 3:5 C:1:25 D:9:25
2)把100克白糖放如1000克水中,糖和水的比是( )
a: 1:12 b: 1:11 c : 1:10 d: 1:9
3)比的前项扩大2倍,后项缩小2倍,比值( )
六年级数学《比和比例》知识点

六年级数学《比和比例》知识点一、比的意义和性质1、比的意义两个数相除又叫做两个数的比。
2、比的性质比的前项和后项同时乘上或者除以相同的数(0除外),比值不变。
3、比的应用通过比可以应用一些问题。
二、比例的意义和性质1、比例的意义表示两个比相等的式子叫做比例。
2、比例的性质在一个比例中,组成比例的两个数,叫做比例的项。
在一比例里,两外项的积等于两内项的积。
这叫做比例的基本性质。
3、解比例根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。
这个求未知项的过程,叫做解比例。
三、正比例和反比例1、成正比例的量如果两种量是相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量。
2、成反比例的量如果两种量是相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量。
3、正比例和反比例的判断方法判断两种量是否成正比例或反比例的方法:一是看这两种相关联的量中相对应的两个数的比值是否一定;二是看这两种量中相对应的两个数的积是否一定。
比的意义:两个量的关系可以用比来表示,我们通常称之为“比”。
定义:在两个量的比中,我们把数量放在前面,单位“1”放在后面,我们称之为前项,后项。
比与除法、分数的关系:比的前项相当于被除数或分子,后项相当于除数或分母,比值相当于商或分数值。
比的性质:比的前项和后项同时乘上或者除以相同的数(0除外),比值不变。
比例的意义:表示两个比相等的式子叫做比例。
组成比例的四个数叫做比例的项。
两外两项叫做内项,中间两项叫做外项。
如果中间的两项是两个相同的数,这样的比例叫做对称比例。
比例尺的意义:我们把图上距离和实际距离的比叫做比例尺。
我们把比例尺分为放大比例尺和缩小比例尺两种。
缩小比例尺的计算方法:已知实际距离求图上距离,根据公式计算即可;已知图上距离求实际距离根据公式计算即可。
小学六年级--比和比例知识点梳理
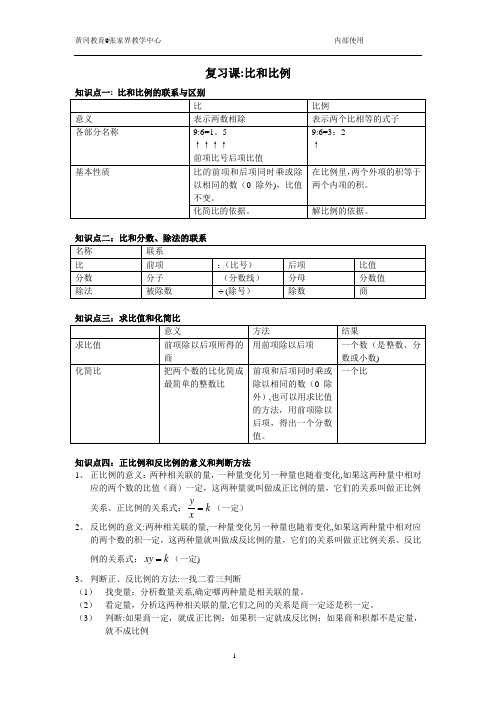
复习课:比和比例知识点三:求比值和化简比 知识点四:正比例和反比例的意义和判断方法 1、 正比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的比值(商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
正比例的关系式:k xy=(一定) 2、 反比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做正比例关系。
反比例的关系式:k xy =(一定)3、 判断正、反比例的方法:一找二看三判断(1) 找变量:分析数量关系,确定哪两种量是相关联的量。
(2) 看定量,分析这两种相关联的量,它们之间的关系是商一定还是积一定。
(3) 判断:如果商一定,就成正比例;如果积一定就成反比例;如果商和积都不是定量,就不成比例知识点五:用比例知识解决问题1、按比例分配问题(1)按比例分配应用题:把一个量按照一定的比分配成几部分,求每个部分数量各是多少的应用题叫做按比例分配应用题。
(2)解题方法一般方法:把比转化成为分数,用分数方法解答,即先求出总分数,然后求出各部分量占总量的几分之几,最后按照求一个数的几分之几多少的解题方法,分别求出各部分的量是多少归一法:把比看做分得的分数,先求出各部分的总分数,然后再用“总量÷总份数=平均每份的量(归一)",再用“一份的量⨯各部分量所对应的份数”,求出各部分的量.用比例知识解答:首先设未知量为。
再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x的比例式,再解比例求出x。
2、用正、反比例知识解答应用题的步骤(1)分析数量关系。
判断成什么比例.(2)找等量关系。
如果成正比例,则按等比找等量关系式;如果成反比例,则按等积找等量关系式。
(3)解比例式。
设未知数为x,并代入等量关系式,得正比例式或反比例式.(4)解比例。
(5)检验并写出答语.精讲典型题例题1(1)一项工程,甲单独做要4天,乙单独做要5天完成,甲和乙的工作效率比是():()(2)把2米:4厘米化成最简单的整数比是(),比值是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
比
比的概念:a ,b 是两个数或者两个同类的量,为了把b 和a 相比较,将a 和b 相除,叫
做a 和b 的比,记作a:b 或写成b
a
,其中b ≠0;读作a 比b 或a 与b 的比。
比值:在a :b 中,a 叫做比的前项,b 叫做比的后项,前项a 除以后项b 所得的商叫做比
值。
(比值是一个数,可以用分数、小数或整数表示。
)
即:比的前项相当于分数的分子和除法中的被除数;
比的后项相当于分数的分母和除法中的除数; 比值相当于分数的分数值和除法中的商。
除法商不变性质:被除数和除数同时乘以或者除以相同的数(0除外)它们的商不变。
分数的基本性质:分数的分子与分母都乘以或者都除以同一个不为零的数,所得的分数与
原分数的大小相等。
比的基本性质:比的前项和后项同时乘以或者除以相同的数(0除外),比值不变。
可以化为最简整数比。
注意:
1、整数比的化简就是用比的前项和后项同时除以它们的最大公因数,直至两个前项和后项互素;
2、分数比的化简可以把比式看成除式,直接进行分数除法运算(如果用除法化简的结果是整数,那么分母1不能省略,把商化成比的形式);
3、小数比的化简先把比的前项和后项化成整数,再来化简;
4、带有单位的比的化简,先把单位统一后在化简。
1
2
互素),
然后再比例尺=图上距离:实际距离
比例
比例:a、b、c、d四个量中,如果a:b=c:d,那么就说a、b、c、d成比例,也就是表示两个比相等的式子叫做比例。
(其中a、b、c、d分别叫做第一、二、三、四比例项,第一比例项a和第四比例项d叫做
比例外项;第二比例项b 和第三比例项c 叫做比例内项。
)
如果两个比例内项相同,即a :b=b :c ,那么把b 叫做a 和c 的比例中项。
比例的基本性质:(内项之积等于外项之积)
即,如果a :b=c :d 或d c
b a =,那么ad=b
c ,反之,如果a 、b 、c 、
d 都不为零,且ad=bc ,
那么a :b=c :d 或d
c
b a =。
比例的基本性质可进行比例变形,常用的变形有:d
c
b a =
1、交换两内项得:b
a
23
作n%
小数化成百分数:小数化成百分数,将小数点向右移两位,同时在右面添加百分号。
百分数化成小数:将百分号前的数字的小数点向左移两位,同时去掉后面的百分号。
(分数化成小数不能除尽用“≈”,小数化成百分数用“=”。
)
百分比的实际应用
100⨯=
总人数
及格人数
及格率%
100⨯=
产品总数合格产品数
合格率%
100⨯=
原来的产量
增加的产量
增产率%
100⨯=
应该出勤人数实际出勤人数
出勤率%
100⨯=
得票数
得票率%
利息
等可能事件
概率:对于一个随机事件A 我们把表示其发生可能性大小的数值称为随机事件A 发生的
概率,记为P (A ) P=
所有等可能的结果数发生的结果数
(P 是概率的英文单词probability 首字母)。
