初高中衔接基本不等式的解法
常见不等式通用解法

常见不等式通用解法总结一、基础的一元二次不等式,可化为类似一元二次不等式的不等式 ①基础一元二次不等式如2260x x --<,2210x x -->,对于这样能够直接配方或者因式分解的基础一元二次不等式,重点关注解区间的“形状”。
当二次项系数大于0,不等号为小于(或小于等于号)时,解区间为两根的中间。
2260x x --<的解为3(,2)2-当二次项系数大于0,不等号为大于(或大于等于号)时,解区间为两根的两边. 2210x x -->的解为(,1(1)-∞⋃+∞当二次项系数小于0时,化成二次项系数大于0的情况考虑。
②可化为类似一元二次不等式的不等式(换元)如1392x x +->,令3x t =,原不等式就变为2320t t -+<,再算出t 的范围,进而算出x 的范围 又如2432x ax >+,令2t x =,再对a 进行分类讨论来确定不等式的解集 ③含参数的一元二次不等式解法步骤总结:如不等式210x ax ++>,首先发现二次项系数大于0,而且此不等式无法直接看出两根,所以,讨论24a ∆=-的正负性即可。
此不等式的解集为0,0,{|}20,()R a x R x ⎧⎪∆<⎪⎪∆=∈≠-⎨⎪⎪⎪∆>-∞⋃+∞⎩又如不等式223()0x a a x a -++>,发现其可以通过因式分解化为2()()0x a x a -->,所以只需要判定2a 和a 的大小即可。
此不等式的解集为2201,{|}01,(,)(,)01,(,)(,)a or a x R x a a a a a or a a a ==∈≠⎧⎪<<-∞⋃+∞⎨⎪<>-∞⋃+∞⎩又如不等式22(1)40ax a x -++>,注意:有些同学发现其可以因式分解,就直接写成(2)(2)0ax x -->,然后开始判断两根2a和2的大小关系,这样做是有问题的。
不等式解法的精辟总结
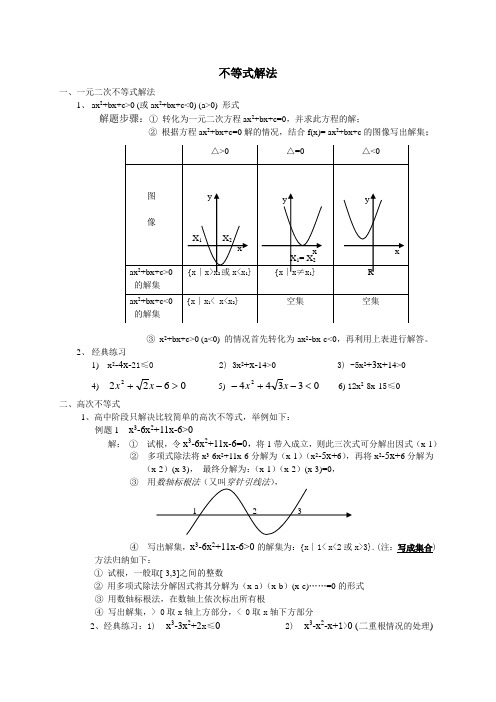
不等式解法一、一元二次不等式解法1、 ax 2+bx+c>0 (或ax 2+bx+c<0) (a>0) 形式解题步骤:① 转化为一元二次方程ax 2+bx+c=0,并求此方程的解;② 根据方程ax 2+bx+c=0解的情况,结合f(x)= ax 2+bx+c 的图像写出解集;③ x 2+bx+c>0 (a<0) 的情况首先转化为-ax 2-bx-c<0,再利用上表进行解答。
2、 经典练习1) x 2-4x-21≤0 2) 3x 2+x-14>0 3) -5x 2+3x+14>04) 06222>-+x x 5) 033442<-+-x x 6) 12x 2-8x-15≤0二、高次不等式1、高中阶段只解决比较简单的高次不等式,举例如下:例题1 x 3-6x 2+11x-6>0解: ① 试根,令x 3-6x 2+11x-6=0,将1带入成立,则此三次式可分解出因式(x-1)② 多项式除法将x 3-6x 2+11x-6分解为(x-1)(x 2-5x+6),再将x 2-5x+6分解为 (x-2)(x-3), 最终分解为:(x-1)(x-2)(x-3)=0,③④ 写出解集,x 3-6x 2+11x-6>0的解集为:{x ∣1< x<2或x>3}.(注:写成集合) 方法归纳如下:① 试根,一般取[-3,3]之间的整数② 用多项式除法分解因式将其分解为(x-a )(x-b )(x-c)……=0的形式③ 用数轴标根法,在数轴上依次标出所有根④ 写出解集,> 0取x 轴上方部分,< 0取x 轴下方部分2、经典练习:1) x 3-3x 2+2x ≤0 2) x 3-x 2-x+1>0 (二重根情况的处理)。
高中数学基本不等式的解法十例

解 析 : 由 三 点 共 线 可 得 a b 1 , 观 察 形 式 采 用 “1” 的 代 换 , 故 而
1
1
1 a
1 b
a
b
2
b
a
,等式右侧积为定值,故而利用积定和最小法则可
ab
1
ab
得 : b a 2 ba 2 , 当 且 仅当 b aab1 时 取 等号 。故 而 可 得
a b ab
2x 2y
42x
y
2
2x 2y 42x y 4 , 当 且 仅 当
2x y 2x 2y
2x y 2x 2y
2x 2y 2x y
42x y
2x 2y
2 ,亦即
x
y
0 3 2
时取等号。此时可得 4 x
3y min
9 2
。
问题 3:方程中的基本不等式
解题思路:将需要利用不等式的项移到方程的一边,利用基本不等式求解即可。
3
2
3 a
2 b
2a
3b
12
9b a
4a b
,观察分子可得分子积为定值,根据积定和
ab
6
6
最小法则可得: 9b 4a 2
ab
9b a
4a b
12
,当且仅当
9b a
4a b
a b
3 2
1
时取等号,故
而可得
3
2
12
9b a
4a b
4
。
ab
6
(不等式与解三角形)例题 7: .
中,角
的对边分别为
a
2
b
2
ab
可
得
基本不等式题型及常用方法总结

基本不等式题型及常用方法总结基本不等式题型包括一元一次不等式、一元二次不等式、绝对值不等式和有理不等式等。
1. 一元一次不等式:- 解法1:通过移项和化简来求解,确保不等号方向的正确性。
- 解法2:将不等式转化为等价的集合表示,再通过集合的交、并运算求解。
2. 一元二次不等式:- 解法1:将不等式化为一元二次函数的图像,通过观察图像求解或者利用函数的性质来求解。
- 解法2:通过移项和配方法将不等式转化为二次函数的标准形式,再判断二次函数图像的位置与不等号关系来求解。
3. 绝对值不等式:- 解法1:将绝对值不等式分段求解,分别讨论绝对值内部是正数还是负数的情况。
- 解法2:通过绝对值的定义和不等式的性质,将绝对值不等式转化为两个简单的不等式来求解。
4. 有理不等式:- 解法1:将有理不等式化为分式的形式,然后通过分式的性质来求解。
- 解法2:通过变量的替换来将有理不等式转化为一元二次不等式或者一元一次不等式,再利用对应的方法来求解。
常用方法总结:1. 对于一元一次不等式和一元二次不等式,常用的方法是移项和化简、画函数图像和利用函数的性质来求解。
2. 对于绝对值不等式,常用的方法是分段求解和利用绝对值的性质来求解。
3. 对于有理不等式,常用的方法是化为分式形式和利用分式的性质来求解。
4. 在求解不等式的过程中,经常需要进行合并同类项、开方、取倒数、乘除等基本运算,需要注意运算法则和符号的变化。
5. 在不等式的求解过程中,需要注意不等式两边的平方值是否相等,以及是否存在不等式的等价变换等。
同时,在进行运算过程中,需要根据不等式的符号关系来选择合适的方式。
不等式的解题方法与技巧

不等式的解题方法与技巧不等式是数学中的一个重要概念,解不等式不仅是中学阶段数学学习的一部分,也是高中阶段进一步学习函数与分析的基础。
下面将介绍一些解不等式的常用方法和技巧。
1.基本不等式性质对于两个不等式a<b和c<d,可以根据其性质进行合并或分拆:-合并:a+b<c+d-分拆:a-b>c-d2.不等式化简对于复杂的不等式,可以通过一系列的等价变形将其化简为简单的形式。
常用的等价变形方法有:- 同乘或同除以一个正数:如果a<b,则对于正数x,有ax<bx;如果a<b且x>0,则有ax<bx;如果a<b且x<0,则有ax>bx。
-同加或同减一个具体数:如果a<b,则对于任意实数x,有a+x<b+x,即a+c<b+c;同理,a-c<b-c。
-综合运用:通过多次变换,将不等式化为更简洁的形式。
3.不等式乘法法则不等式乘法法则用于解决乘法不等式的问题。
对于两个正数a和b,以及一个不等式c<d,有以下结论:- 如果a<b且c<d,则ac<bd。
- 如果a<b且c>d,则ac>bd。
- 如果a<b且c=d,则ac=bd。
注意:当a和b中至少一个为负数时,上述法则不适用。
4.不等式绝对值性质当不等式中含有绝对值时,可以利用绝对值的性质进行求解。
对于实数a和b,可以根据绝对值性质得到以下结果:-如果,a,<,b,则a^2<b^2-如果,a,>,b,则a^2>b^2-如果,a,=,b,则a^2=b^25.不等式取正负号问题当不等式的系数为负数时,可以通过取正负号的方式,将其转化为求解不等式的问题。
具体方法如下:-如果a<0,则对不等式两边同时取负号,得到-a>-b。
-如果a>0,则对不等式两边同时取正号,得到a<b。
6.解多项式不等式对于多项式不等式,可以通过求解其零点,确定其正负性。
基本不等式的解法高中数学

基本不等式的解法高中数学基本不等式是数学中常见且重要的一种不等式,它可以帮助我们解决很多问题。
在解决问题时,我们经常会遇到需要比较大小关系的情况,而基本不等式提供了一种有效的方法。
我们来看一下什么是基本不等式。
基本不等式是指对于任意实数a 和b,有以下三个基本不等式成立:1. 加减法法则:如果a>b,则对于任意实数c,有a+c>b+c,a-c>b-c成立。
2. 乘法法则:如果a>b且c>0,则ac>bc成立;如果a>b且c<0,则ac<bc成立。
3. 除法法则:如果a>b且c>0,则a/c>b/c成立;如果a>b且c<0,则a/c<b/c成立。
基本不等式的解法主要有两种常见的方法:代入法和变形法。
我们来介绍代入法。
代入法是指将不等式中的某个变量用其他已知条件表示出来,然后代入到不等式中进行比较。
这种方法常用于求两个变量之间的大小关系。
例如,我们要证明当x>0时,有x^2>0成立。
我们可以将x表示为x=√(x^2),然后将其代入到不等式中,得到(√(x^2))^2>x^2,即x^2>x^2,显然成立。
我们来介绍变形法。
变形法是指通过对不等式进行变形,使其更易于比较大小关系。
这种方法常用于求不等式的最值或者一元函数的单调性。
例如,我们要证明当x>0时,有x+1/x>2成立。
我们可以通过变形将不等式转化为x^2-2x+1>0,然后求出该二次函数的判别式,发现其大于零,即该二次函数的图像在x轴上方,从而得到不等式成立。
基本不等式还可以用于求解一些实际问题。
例如,我们要找到一个数x,使得其与另一个已知数的和最小。
我们可以设所求数为x,已知数为a,根据基本不等式的加减法法则,有x+a>x,即a>0。
因此,我们可以得出结论,所求数与已知数的和最小值为0。
基本不等式在数学中的应用非常广泛,不仅可以用于解决代数问题,还可以用于解决几何问题、概率问题等。
中学学习常用不等式技巧 不等式问题解决之道
中学学习常用不等式技巧不等式问题解决之道中学学习常用不等式技巧 - 不等式问题解决之道在中学数学学习中,不等式是一个重要且常见的概念。
它与等式相比,更能反映数的大小关系,因此对于解决实际问题有着重要的作用。
本文将介绍一些中学学习中常用的不等式技巧,以帮助学生更好地解决不等式问题。
一、绝对值不等式技巧在处理绝对值不等式时,常见的技巧包括:1. 利用绝对值的定义进行分情况讨论。
例如,对于不等式|2x-3|<5,根据绝对值的定义可得到两种情况下的不等式:2x-3<5和-(2x-3)<5,进而求解出x的取值范围。
2. 利用绝对值的性质转化为含有绝对值的等式。
例如,对于不等式|2x-5|>3,可以将其转化为两个不等式:2x-5>3或2x-5<-3,再求解得到x的取值范围。
二、平方不等式技巧平方不等式是中学数学中常见的一类不等式。
在解决平方不等式时,有以下几种常用的技巧:1. 利用平方的性质进行不等式变形。
例如,对于不等式x²-4x>0,可以将其变形为x(x-4)>0,再根据乘法的性质求解得到x的取值范围。
2. 利用平方的非负性进行分情况讨论。
例如,对于不等式x²-5x+6≥0,可以将其分解为(x-2)(x-3)≥0,再根据乘积非负的条件讨论两种情况下x的取值范围。
三、倒数不等式技巧在处理倒数不等式时,常常会用到以下的技巧:1. 利用倒数的性质进行不等式变形。
例如,对于不等式1/(x-2)>3,可以将其变形为x-2<1/3,再求解得到x的取值范围。
2. 利用倒数的符号性质进行分情况讨论。
例如,对于不等式1/(x+2)>0,根据倒数的性质可知,当x+2>0时,不等式成立;当x+2<0时,不等式不成立。
四、复合不等式技巧在解决复合不等式问题时,可以利用以下的技巧:1. 利用复合不等式的性质进行变形。
例如,对于不等式-2<x-3<4,可以将其分解为-2<x-3和x-3<4,再分别求解得到x的取值范围,并求其交集。
基本不等式的各种求解方法和技巧
基本不等式一、知识梳理二、极值定理(1)两个正数的和为常数时,它们的积有 ;若0,0,a b a b M >>+=,M 为常数,则ab ≤ ;当且仅当 ,等号成立.简述为,当0,0,a b a b M >>+=,M 为常数,max ()ab = .(2)两个正数的积为常数时,它们的和有 ;若0,0,a b ab P >>=,P 为常数,则a b +≥ ;当且仅当 ,等号成立.简述为,当0,0,a b ab P >>=,M 为常数,min ()a b += .(,)2a b a b R ++≤∈,求最值时应注意以下三个条件:应用基本不等式的经典方法方法一、直接利用基本不等式解题例1、(1)若0,0,4a b a b >>+=,则下列不等式恒成立的是( )A .112ab > B .111a b +≤ C 2≥D. 2211+8a b ≤(2)不等式2162a bx x b a +<+对任意(),0,a b ∈+∞ 恒成立,则实数x 的取值范围是() A .(2,0)− B .(,2)(0,)−∞−+∞ C .(4,2)−D .(,4)(2,)−∞−+∞(3)设,,1,1x y R a b ∈>>,若3,x y a b a b +,则11x y +的最大值为 ( )A .2B .32C .1D .12方法二:凑项(增减项)与凑系数(利用均值不等式做题时,条件不满足时关键在于构造条件,通过乘或除常数、拆因式、平方等方式进行构造) 例2、(1)已知54x <,求函数1445y x x =+−的最大值;(2)已知,则的取值范围是() A . B . C. D .方法三:“1”的巧妙代换命题点1、“1”的整体代换例3、(1)若正数,x y 满足35x y xy +=,则34x y +的最小值是() A .245 B .285 C .5D .6(2)已知0,0,x y >>且21x y +=,求11x y +的最小值.0,2b a ab >>=22a b a b +−(],4−∞−(),4−∞−(],2−∞−(),2−∞−命题点2、“1”的部分代换(3)已知0,0,x y >>且21x y +=,求1x x y +的最小值.(4)(2013·天津高考理科)设a + b = 2, b >0, 则当a = 时,1||2||a a b +取得最小值.命题点3、“1”的变形代换(5)设0,1a b >>,若3121a b a b +=+−,则的最小值为 .(6)已知实数,x y 满足102x y x y >>+=,且,则213x y x y++−的最小值为________.(7)设10<<x ,,a b 都是大于0的常数,则x b x a −+122的最小值为 .方法四: 消元(转化为函数最值,此时要注意确定变量的范围)例4、(1)已知,,x y z R +∈,230x y z −+=,则2y xz 的最小值 .(2)设正实数,,x y z 满足22340x xy y z −+−=,则当xy z 取得最大值时, 212x y z +−的最大值为 .方法五:“之和”与“之积”的互化例5、(1)已知a ,b 为正实数,2b +ab +a =30,则1ab的最小值 .(2)已知0x >,0y >,228x y xy ++=,则2x y +的最小值是 .方法六、连续两次使用基本不等式求最值例6、(1)(2009重庆卷)已知0,0a b >>,则11a b++ )A .2B .C .4D .8(2)已知22log log 1+≥a b ,则39a b+的最小值为__________(3)若 的最小值为 .方法七、利用基本不等式求分式函数最值例7、(1)当1x >−时,求1()21f x x x =++的最小值.(2)求函数y =的值域。
第06讲 基本不等式(学生版)-2023年新高一(初升高)暑期数学衔接(新人教版)
第06讲基本不等式【学习目标】1.掌握基本不等式),02a b a b +≥>2.结合具体实例,能用基本不等式解决简单的最大值或最小值的问题.【基础知识】一、几个重要的不等式1.ab ≤a +b 2(a >0,b >0)2.a 2+b 2≥2ab (a ,b ∈R ).3.b a +a b≥2(a ,b 同号).4.ab (a ,b ∈R ).5.a 2+b 22≥(a ,b ∈R ).以上不等式等号成立的条件均为a =b .二、算术平均数与几何平均数设a >0,b >0,则a ,b 的算术平均数为a +b 2,几何平均数为ab ,基本不等式可叙述为两个正数的算术平均数不小于它们的几何平均数.三、利用基本不等式求最值问题已知x >0,y >0,则1.如果积xy 是定值p ,那么当且仅当x =y 时,x +y 有最小值2p .(简记:积定和最小)2.如果和x +y 是定值p ,那么当且仅当x =y 时,xy 有最大值p 24.(简记:和定积最大)3.应用基本不等式时的三个关注点(1)一正数:指式子中的a ,b 均为正数.(2)二定值:只有ab 为定值时才能应用基本不等式,因此有时需要构造定值.(3)三相等:即“=”必须成立,求出的定值才是要求的最值.4.在利用基本不等式求最值时,要根据式子的特征灵活变形,配凑出积、和为常数的形式,然后再利用基本不等式.凑配法求最值的基本技巧:①配凑系数;②配凑常数;③配凑分子;④配凑分母;⑤配凑项数5.条件最值的求解通常有两种方法:一是消元法;二是将条件灵活变形,利用常数“1”代换的方法构造和或积为常数的式子,然后利用基本不等式求最值.求1a +1b型最值问题,常通过“1”来进行转化,但不是所有的最值都可以通过基本不等式解决,有一些看似可以通过基本不等式解决的问题,由于条件的限制,等号不能够成立,这时就不能用基本不等式来解决,而要借助于其他求值域的方法来解决.四、基本不等式的其他应用1.基本不等式除具有求最值的功能外,还具有将“和式”转化为“积式”以及将“积式”转化为“和式”的放缩功能,常用于比较数(式)的大小2.一般地,对含参的不等式求范围问题通常采用分离变量转化为恒成立问题,对于“恒成立”的不等式,一般的解题方法是先分离然后求函数的最值.另外,要记住几个常见的有关不等式的等价命题:(1)a >f (x )恒成立⇔a >f (x )max ;(2)a <f (x )恒成立⇔a <f (x )min ;(3)a >f (x )有解⇔a >f (x )min ;(4)a <f (x )有解⇔a <f (x )max .3.利用基本不等式证明不等式的策略从已证不等式和问题的已知条件出发,借助不等式的性质和有关定理,经过逐步的逻辑推理,最后转化为所求问题,其特征是以“已知”看“可知”,逐步推向“未知”.对不能直接使用基本不等式的证明可重新组合,形成基本不等式模型,再使用.4.构造不等式求范围利用a b +≥或ab≤22a b +⎛⎫ ⎪⎝⎭将式子转化为含ab 或a+b 的一元二次不等式,将ab ,(a+b)作为整体解出范围5.函数法求最值:若利用基本不等式时等号取不到,则无法利用基本不等式求最值,则可将要求的式子看成一个函数,利用函数的单调性求最值.6.利用基本不等式解决实际问题的步骤解实际问题时,首先审清题意,然后将实际问题转化为数学问题,再利用数学知识(函数及不等式性质等)解决问题.用基本不等式解决此类问题时,应按如下步骤进行:(1)先理解题意,设变量,设变量时一般把要求最大值或最小值的变量定为函数.(2)建立相应的函数关系式,把实际问题抽象为函数的最大值或最小值问题.(3)在定义域内,求出函数的最大值或最小值.(4)正确写出答案.【考点剖析】考点一:利用基本不等式判断命题的真假例1.(2022学年江西省赣州市赣县高一下学期开学考试)下列说法正确的为()A .12x x+≥B .函数224x y +=4C .若0,x >则(2)x x -最大值为1D .已知3a >时,43+≥-a a 43=-a a 即4a =时,43+-a a 取得最小值8考点二:利用基本不等式比较大小例2.(2022学年黑龙江省哈尔滨市高一上学期期中)若a >0,b >0,且a ≠b ,则()A .2a b +B <2a b +C2a b +D 2a b +考点三:利用基本不等式求最值例3.(2022学年吉林省延边州高一上学期期末)已知2x >,则函数()1222y x x =+--的最小值是()A .B .2C .2D考点四:利用基本不等式求范围例4.(2022学年湖北省黄石市有色第一中学高一上学期期中)设0x >,0y >,且()()114x y --≥,求xy 的取值范围考点五:利用基本不等式证明不等式例5.已知,,a b c 均为正实数,且满足 3.a b c ++=证明:(1)2223b c a a b c++≥;.考点六:利用基本不等式求解恒成立问题例6.已知x >0,y >0,且x +2y =1,若不等式21x y +≥m 2+7m 恒成立,则实数m 的取值范围是()A .﹣8≤m ≤1B .m ≤﹣8或m ≥1C .﹣1≤m ≤8D .m ≤﹣1或m ≥8考点七:基本不等式在实际问题中的应用例7.(2022学年河北省唐县第一中学高一下学期5月月考)冬奥会期间,冰墩墩成热销商品,一家冰墩墩生产公司为加大生产,计划租地建造临时仓库储存货物,若记仓库到车站的距离为x (单位:km ),经过市场调查了解到:每月土地占地费1y (单位:万元)与(1)x +成反比,每月库存货物费2y (单位:万元)与(41)x +成正比;若在距离车站5km 处建仓库,则1y 与2y 分别为12.5万元和7万元.记两项费用之和为ω.(1)求ω关于x 的解析式;(2)这家公司应该把仓库建在距离车站多少千米处,才能使两项费用之和最小?求出最小值.【真题演练】1.(2020-2021学年陕西省榆林市第十中学高一下学期期末)若0a >,0b >且4a b +=,则ab 的最大值为()A .4B .2C .12D .142.(2022学年福建省三明第一中学高一上学期学段考)已知0a >,0b >,2ab =,则下列结论一定成立的是()A .4a b +≥B .4a b +≤C .224a b +>D .11a b+≥3.(2022学年贵州省六盘水红桥学校高一上学期期中)设x ,y ,z 为正实数,满足0x y z -+=,则2y xz 的最小值是()A .4B .2C .12D .144.(2022学年安徽省阜阳市太和县三校高一上学期期中联考)下列命题中正确的是()A .当1x >时,12x x +≥B .当0x <时,12x x +≤-C .当01x <<时,12x x +≥D .当2x ≥时,222x x +≥5.(2022学年甘肃省金昌市永昌县高一上学期期末)已知a >0,b >0,a +b =2,则对于14a b +,下列说法准确的是()A .取得最小值时a =23B .最小值是5C .取得最小值时b =23D .最小值是926.(2022学年安徽省宣城市泾县中学高一上学期10月月考)某项研究表明:在考虑行车安全的情况下,某路段车流量F (单位时间内经过测量点的车辆数,单位:辆/时)与车流速度v (假设车辆以相同速度v 行驶,单位:米/秒),平均车长l (单位:米)的值有关,其公式为2760001820v F v v l =++.如果不限定车型, 6.05l =,则最大车流量为__________辆/时.7.(2022学年广西河池市高一上学期八校联考)已知000a b c >>>,,,求证222a b c ab bc ca ++≥++.8.(2022学年湖北省孝感市高一上学期期中联考)已知0,0,x y >>且1x y +=,求44x y x y+++的最小值.【过关检测】1.(2022学年四川省南充市白塔中学高一下学期月考)已知0ab >,1a b +=,则11a b +的最小值为()A .0.5B .1C .2D .42.(2022学年江西省丰城中学高一下学期入学考试)已知,,x y z 都是正实数,若1xyz =,则()()()x y y z z x +++的最小值为()A .2B .4C .6D .83.(2022学年四川省内江市威远中学校高一下学期阶段性测试)当1x >时,不等式11x a x +≥-恒成立,则实数a 的取值范围是()A .(]2-∞,B .[)2+∞,C .[)3+∞,D .(]3-∞,4.(2022学年河南省开封市高一上学期期末)已知x ,y 都是正数,则下列命题为真命题的是()A .如果积xy 等于定值P ,那么当x y =时,和x y +有最大值2PB .如果和x y +等于定值S ,那么当x y =时,积xy 有最小值214SC .如果积xy等于定值P ,那么当x y =时,和2x y +有最小值D .如果和2x y +等于定值S ,那么当2x y =时,积xy 有最大值218S 5.(多选)(2022学年山东省枣庄市滕州市高一上学期期末)设正实数m n 、满足2m n +=,则()A .12m n +的最小值为B 的最小值为2C 的最大值为1D .22m n +的最小值为26.(多选)(2022学年湖北省部分高中联考协作体高一上学期期中)有下列4个关于不等式的结论,其中正确的是()A .若0x <,则12xx +≤-B .若x ∈R 22≥C .若x ∈R ,则12x x +≥D .若1a >,则1(1)14a a ⎛⎫++≥ ⎪⎝⎭7.(2022学年上海市延安中学高一上学期期中)已知0a >,0b >,2a b +=,则在下列不等式①1ab ≤;②222a b +≥;④112a b+≥;⑤333a b +≥其中恒成立的是___________.(写出所有正确命题的序号)8.已知0x >,0y >,1x y +=,则311y x x y++的最小值为__.9.(2022学年湖北省十堰市车城高中高一上学期9月月考)(1)已知0x >,0y >,112x y+=,求x y +的最小值;(2)已知102x <<,求(12)y x x =-的最大值.10.(2022学年江苏省南通市海安市高一上学期期末)为宣传2022年北京冬奥会,某公益广告公司拟在一张矩形海报纸(记为矩形ABCD ,如图)上设计三个等高的宣传栏(栏面分别为一个等腰三角形和两个全等的直角梯形),宣传栏(图中阴影部分)的面积之和为21440cm .为了美观,要求海报上所有水平方向和竖直方向的留空宽度均为2cm .设直角梯形的高为cm x .(1)当20(2)为节约成本,应如何选择海报纸的尺寸,可使用纸量最少(即矩形ABCD的面积最小)?。
基本不等式的所有公式及常用解法
基本不等式的所有公式及常用解法
基本不等式是数学中一种重要的概念,它可以帮助我们解决许多复杂的问题。
基本不等式的公式有许多,其中最常用的是加法不等式、乘法不等式、减法不等式和比较不等式。
加法不等式的公式是:若a、b是任意实数,则有a+b≥0。
加法不等式的解法是:若a、b是
任意实数,则可以将a+b≥0转化为a≥-b,从而得出a的取值范围。
乘法不等式的公式是:若a、b是任意实数,则有ab≥0。
乘法不等式的解法是:若a、b是任
意实数,则可以将ab≥0转化为a≥0或b≥0,从而得出a、b的取值范围。
减法不等式的公式是:若a、b是任意实数,则有a-b≥0。
减法不等式的解法是:若a、b是
任意实数,则可以将a-b≥0转化为a≥b,从而得出a的取值范围。
比较不等式的公式是:若a、b是任意实数,则有a>b或a<b。
比较不等式的解法是:若a、b
是任意实数,则可以将a>b或a<b转化为a-b>0或a-b<0,从而得出a的取值范围。
基本不等式的公式和解法可以帮助我们解决许多复杂的问题,它们在生活中也有着重要的作用。
比如,当我们在购物时,可以利用基本不等式的公式和解法来比较价格,从而节省购物费用。
此外,基本不等式的公式和解法还可以帮助我们解决许多其他的问题,比如计算投资回报率、计算贷款利息等。
总之,基本不等式的公式和解法对我们的生活娱乐有着重要的意义,它们可以帮助我们解决许多复杂的问题,节省购物费用,计算投资回报率和贷款利息等。
