导电媒质中的平面电磁波
平面电磁波

例如铜:
f 1MHz, c 66106 m
f 30GHz, c 0.38106 m
4.4 电磁波的极化
本节要点
极化 线极化 圆极化 椭圆极化
1. 极化(polarization)
金属导体 金属导体
导体上的感应电 动势等于零
导体上的感应电 动势最大
无耗媒质中电场、磁场与功率流
4.2 无限大导电媒质中的平面电磁波
本节要点
复介电常数 导电媒质中的平面波 色散及其对通信的影响
1.复介电常数(complex permittivity)
无限大导电媒质中复介电常数
~ 1 j
实部代表位移电流的贡 献,不会引起能量消耗。
+z轴方向传播的均匀平面波 -z轴方向传播的均匀平面波
4. 均匀平面波的基本概念
如果电介质区无限延伸,则电场矢量可一般地表示为 E ax E0e jkz 时域表达式为 Ex z, t E0 cost kz 0
下面,我们对平面波进行较为详细的分析。
代表场的波动状态,称为电磁波的相位。它由三部分构成:
~ 将无耗媒质的相位常数及波阻抗中的 均以 来取代,即 得导电媒质中的复相位常数为
~ ~ k j
~ 1 j
2 1 1 1 2 1 2
~ 1 j
2
2.导体中均匀平面电磁波
导体中均匀平面波的电磁场及平均坡印廷矢量为
Ex E0ez e jz
Hy
E0e z e jz e j / 4
9. 平面波解析

的存在与否,将波分为三种类型 和H 根据 E
z
z
1.TEM 波
( Ez 0, H z 0,
Kc 0)
说明任一时刻,在xoy平面上场的分布与稳态场相同
0, H 0 ),亦称横电波 2.TE 波( E
z z
3.TM 波(
z 0, H z 0 E
),亦称横磁波
(9 - 2 - 1)
图 9-1 均匀平面电磁波的传播
综上可见,可取:
E e x Ex ( z, t )
E x ( z, t ) 1 E x ( z, t ) 2 0 2 2 z t
2 2
(9-2-2)
此方程的通解为
Ex ( z, t ) f1 ( z t ) f 2 ( z t )
E E E 2 t t
2 2
(9-1-2)
类似的推导可得
H H H 2 t t
2 2
(9-1-3)
相量形式的波动方程:
E +k E 0
2 2 2
H +k H 0
2
(9-1-4)
其中:
k c
2
c j 1 j
Z(z)=A+ ez + A-ez
2 T E0 ( x, y )+K c 2 E0 ( x, y ) 0 2 T H0 ( x, y )+K c 2 H0 ( x, y ) 0
(9-1-5)
K c c +
2 2
2
(9-1-5)分成纵向成分和横向成分:
2 T E0T ( x, y )+Kc 2 E0T ( x, y ) 0 2 T H0T ( x, y )+Kc 2 H0T ( x, y ) 0 2 T E0z ( x, y )+Kc 2 E0z ( x, y ) 0 2 T H0z ( x, y )+Kc 2 H0z ( x, y ) 0
第六章平面电磁波

1
2
1
二、导电媒质中平面电磁波的传播特性
1、不良导体主要参数(不能近似,计算复杂)
2、电介质主要参数(如聚四氟乙烯、聚苯乙烯、石英等)
表明:相移常数和波阻抗近似与理想电介质相同,衰减常数与 频率无关,正比于电导率。因此均匀平面电磁波在低损耗质中 的传播性,除了由微弱的损耗引起的振幅衰减外,与理想媒质 中的传播特性几乎相同。 3、良导体主要参数
表明:任一时刻电场能量密度和磁场能量密度相等,各为总电磁能量一半。 9、电磁能量平均值:
10、能量传播速度: 表明:均匀平面电磁波的能量传播速度等于相速。
z
P161 例6-1 略 补充例题:
• 6-2
P203作业2009.4.28
§6.2 导电媒质中的平面电磁波
一、导电媒质中平面电磁波的传播特性
方程的实际解:(由于无界媒质中不存在反射波)
由于:
二、均匀平面波的传播特性
可得:
振幅
时间相位
空间相位
初相
相位,代表场 的波动状态
上边两式表明:正弦均匀平面电磁波的电场和磁场在空间上互 相垂直,在时间上是同相的,它们的振幅之间有一定的比值,此比 值取决于煤质的介电常数和磁导率。
Ex
z Hy
图 6-3 理想介质中均匀平面电磁波的 上图表示 t = 0 时刻,电场及磁
4、坡印廷矢量的瞬时值
v
v
v
S(z,t) E(z,t) H (z,t)
evz
1 2
Em2
c
e2 az [cos
cos(2t
2
z
20
)]
5、复坡印廷矢量
v S
1 2
v E
v H*
导电媒质均匀平面波
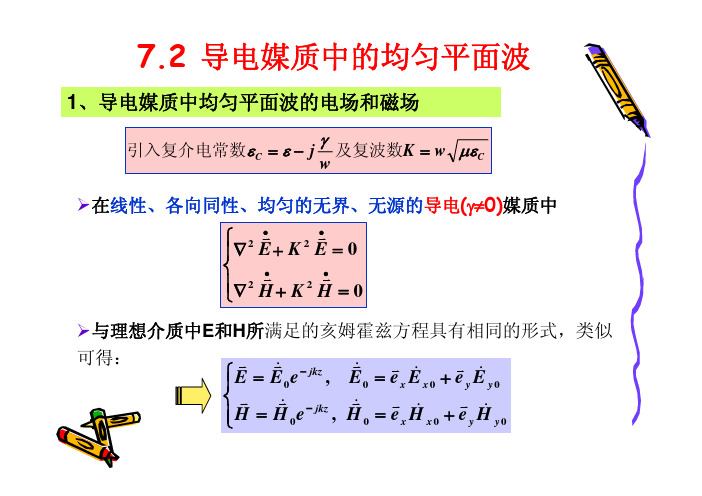
7.2 导电介质中的均匀平面波——2、导电媒质中均匀平面波的传播特性3)媒质导电性对场的影响媒质的导电性由比值 γ < 10 2 wε 1/ 2 γ γ Q K = w με c = w με 1 j ≈ w με 1 j wε 2 wε γ 决定,不仅与媒质特性有关,还与频率有关 wε(1)良介质μ μ γ = ηc = 1 j εc ε wε 1 / 2≈μ γ 1+ j ε 2 wε γ μ 1 , β ≈ w με , V p ≈ α ≈ 2 ε με 1 μ γ μ λ ≈ f με , η c = ε 1 + j 2 wε ≈ ε 平面波在良介质中的传播特性与理想介质中的平面波十分相似 只有微弱损耗引起的衰减,E和H时间相位差极小近似为07.2 导电介质中的均匀平面波——2、导电媒质中均匀平面波的传播特性(1)良导体γ Q K = w με c = w με 1 j wε γ > 100 wε1/ 2γ ≈ w με j 2 wε 1/ 2= wμγ e jπ / 4 = (1 j ) j2 γ = w με e 2 wε wμγπ1/ 22μ μ γ = ηc = 1 j εc ε wε 1 / 2μ γ ≈ j ε wε 1 / 2≈wμγejπ4= (1 + j )wμ 2γ7.2 导电介质中的均匀平面波——2、导电媒质中均匀平面波的传播特性 πf wμγ w 2w Vp = ≈ α≈β ≈ = πfμγ , =2 μγ β μγ 2 wμ j π wμ 2 π λ = 2π ≈ 2π 4 e = (1 + j ) , ηC = =2 wμγ fμγ β γ 2γ 良导体中,均匀平面波为色散波γ越大,电磁波的传播速度越慢,波长越短f=465MHz的电磁波在铜(γ=6.8×107s/m)中传播,其相速为 283.15m/s,波长为0.018mm电场相位超前磁场相位π/4, |ηc|<<1 wm>>we, 平均功率流密度沿波的传播方向按指数规律e-2αz衰减,而场的振幅 按e-αz衰减, γ越大衰减越快(趋肤效应)v 1 v v * v 1 2 γ 2αz Sc = E × H = ez E0 e (1 + j ) 2 2 2 μwv 1 2 γ 2αz S av = e z E 0 e 2 2 μw7.2 导电介质中的均匀平面波——2、导电媒质中均匀平面波的传播特性例7-2-1 有一均匀平面波,在海水中(εr=80,μr=1,γ=4s/m),v v 7 沿+z方向传播,在z=0处,E = e x 100 cos 10 π t(2)确定E的振幅衰减为z=0处的1%时的z值;() (V / m )(1)求其衰减常数α,相位常数β,相速Vp,波长λ及波阻抗ηc; (3)写出E(z,t)和H(z,t)在z=0.8m处的函数表示式分 析:v v Q E (z = 0 , t ) = e x 100 cos 10 7 π t() w = 10 7 πγ γ 4 = = = 180 > 100,为良导体 1 w ε w ε 0ε r 107 π × 10 9 × 80 36πwμγ 107 π × 4π × 10 7 × 4 (1)α ≈ β ≈ = = 8.89 ( Np / m ) 2 2 2π 2π w 107 π = = 0.707(m ) λ= Vp = = = 3.53 × 10 6 (m / s ) β 8.89 β 8.89ηC =wμγejπ4π j 107 π × 4π × 10-7 j π = e 4 = πe 4 (Ω ) 47.2 导电介质中的均匀平面波——2、导电媒质中均匀平面波的传播特性(2)波的振幅按 e αz 规律衰减,设 z = z1处,波的振幅衰减为 z = 0处的1%e( 3)α v v Q E (z = 0 , t ) = e x 100 cos 10 7 π t v v E (z , t ) = e x 100 e α z cos 10 7 π t - β z v v 100 α z H (z , t ) = e y e cos 10 7 π t - β z - θ , η c = η c e jθ αz1= 0.01 z1 = ln 0.01=ηc( ( (4.605 = 0.518(m ) 8.89)))v v (z = 0 .8 , t ) = e x 100 e 8 .89 × 0 .8 cos 10 7 π t - 8 .89 × 0 .8 ∴E v 082 = e x 0。
导电媒质中的波阻抗

2 2
H H
x y
(r (r
) )
k k
2H 2H
x y
(r) (r)
0 0
2H z (r) k 2H z (r) 0
这些方程称为齐次标量亥姆霍兹方程。
由于各个分量方程结构相同,它们的解具有同一形式。
在直角坐标系中,若时变电磁场的场量仅与一个坐标变量有关, 则该时变电磁场的场量不可能具有该坐标分量。
3 z 2
可见,电磁波向正 z 方向传播。
上式中 t 称为时间相位。kz 称
为空间相位。空间相位相等的点组成 的曲面称为波面。
由上式可见, z = 常数的平面为 波面。因此,这种电磁波称为平面波。
因 Ex(z) 与 x, y 无关,在 z = 常 数的波面上,各点场强振幅相等。因 此,这种平面波又称为均匀平面波。
ez
E x z
得
H
e
y
j
E x z
eyHy
Hy
j
E x z
已知电场强度分量 Ex 满足齐次标量亥姆霍兹方程,考虑到
E x x
E x y
0
得
d2Ex dz 2
k 2Ex
0
这是一个二阶常微分方程,其通解为
Ex Ex0e jkz Ex0e jkz
上式第一项代表向正 z 轴方向传播的波,第二项反之。
首先仅考虑向正 z 轴方向传播的波,即 Ex (z) Ex0e jkz
式中Ex0 为 z = 0 处电场强度的有效值。
Ex(z) 对应的瞬时值为
Ez(z, t)
O
2
t1 = 0
t2
T 4
t3
T 2
Ex (z,t) 2Ex0 sin( t kz)
平面电磁波在两种不同媒质中传播特性的比较

电磁波 的应用范 围很广 , 实中几乎无处 不 现
在 。 代 电子技术 如通讯 、 现 广播 、 电视 、 导航 、 达 、 雷 测
( 正或负向) 传播的波。 由平面电磁波的特点可知 , 对于沿 z 轴正向传播的均匀平面电磁波的电磁场场
量 和驯 随时间t 变化外 , 只与波传播方向的坐标 z 有关 , 而与 , 无关, Y 写成数学表达式为
E = (,) H =日(,) tz , tz (. ) 14
控、 电子仪器和测量系统 , 都离不开电磁波的传播 。 电磁波在不同媒质 中传播特性不 同, 在实际生活 中 的应用更是非常广泛 。 下面即在线性、 各向同性、 均
匀的介质 中只有传导电流和位移 电流的情况下, 由
电场强度 和磁 场强度 H 满足 的波 动方 程 出发 , 研
, e
]= c ( t oc一 so
经计算可得出上方程的一般解是
(z [ £ )= ,
+ 2 )
e
]:  ̄ c ( t I. , 一 ;o c o
(. ) 16
由此可得 , 振相沿 正 z 向传播 的速度即波的传播 方 相速度是
=
其中 =七
, 和g f 是任意函数, 其具体形式由初
第2 期
Ma . o 7 r2 o V0. 7 No 2 11 .
平面 电磁波在两种不 同媒质 中传播特性 的 比较
杨延玲L , 刘辉兰 于家峰 ,
(. 1 山东师范大学 物理与微 电子学院, 山东 济南 2 10 ;. 500 2 德州学院 物理 系, 山东 德 州 2 32 ) 50 3
d
可
11 . 无损媒质的特点 无损媒质又称无耗媒质 , 其
7.3_4_5_媒质和介质中的平面波及损耗

1、由σ引起的
j
2、由于介质极化的滞后效应引起的 j ''
复介电常数为
e ' j( '')
损耗角正切
'' tan
'
ε’—传统意义的介电常数( ε )
电磁场与电磁波
20/28
对于一般介质,传输常数:
e [ ' j( '' )] j
sin(2
ft
)
2
3
tan 740.4109 1
良导体
电磁场与电磁波
27
f 1.9104
电磁场与电磁波
16/28
例6-6:均匀平面波f=50MHz,参数(r=16, r,1,=0.02), 求:传播常数,相速度,波长,波阻抗
j
2
2
1
2 2
1
0.92Np / m
2
2
1
2 2
1
r r r
H J D t
r E r
r B
t
•B 0 r
•D
H E
E
H
E t
t
• •
H E
0 0
E [ H t] ( H ) t
得到:
'
1[ 2
1
(
'' / '2
良导体中的的平面波

良导体中的的平面波
良导体中的平面波是一种特殊的电磁波,在导体中传播。
当电
磁波穿过导体时,它会与导体中的自由电子相互作用,导致电磁波
的衰减。
在良导体中,电磁波的传播受到导体电导率的影响,电导
率越高,电磁波的衰减越严重。
在电磁波传播中,平面波是一种特定的波动形式,它的波前是
平坦的,波峰和波谷是平行的。
在良导体中,平面波的传播受到导
体的影响,导体中的自由电子会对电磁波产生阻尼效应,使得平面
波在传播过程中衰减。
这种衰减会导致电磁波的能量逐渐转化为热能,最终被导体吸收。
良导体中的平面波还受到导体内部结构的影响,比如晶格结构、缺陷等因素都会对平面波的传播产生影响。
此外,频率、波长等也
会影响平面波在良导体中的传播特性。
总的来说,良导体中的平面波受到多种因素的影响,包括导体
的电导率、内部结构以及电磁波的频率和波长等。
这些因素共同作用,决定了平面波在良导体中的传播特性和衰减程度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
vp
2
2
可见,良导体中相速为频率的函数,是色散波,且电导率越大,相 速越慢。
3. 趋肤效应
高频电磁波从表面进入导电媒质越深,场的幅度就越小,能量就越小, 即能量趋于表面,这就是趋肤效应,或集肤效应或趋表效应。
趋肤深度(或集肤深度、穿透深度):当场从表面进入导电媒质中一 段距离后,使得其幅度衰减到表面幅度的1/e倍时,这段距离(或深度) 叫做趋肤深度δ。即
常数。
3. 波阻抗
导电媒质中的波阻抗为
g
c
Ex
g
Hy
j
c
1 j
c e j
可见 c为复数,其模值和相位分别为
c
[1
(
)
2
]
1 4
0
1 arctg 2
0,
4
由上式可知,c 有非零相角,意味着电场与磁场具有不同的相位,相
位差为θ,故(可4)改写为
g
g
H
uuv E
ey
m
vp
1
2
1
2
1
1
2π
2
2π
1
2
1
2π 2π
k
由上可知:
(1)导电媒质中相速要比理想介质中慢,波长要比理想介质中短;
(2)σ愈大,相速vp越慢,波长λ越短; (3)相速与频率有关,故电磁波中不同的频率分量将以不同的相速传播,
经过一定距离后,它们的相位发生不同变化,从而导致信号失真,比,除有微弱损耗引起的振幅
衰减外,其余参量近似相同。
2. 良导体中的均匀平面波
对于良导体:
tg c
?
1
物理意义表示电介质中的传导电流远大于位移电流,相关参数有:
2
c
1 j
2
e
j 4
由此可见,电阻部分和电抗(呈感性)部分相等,即c 的相角为45o。
主要内容
❖ 导电媒质中均匀平面波的传播特性 ❖ 集肤效应
学习目的
❖ 掌握导电媒质与无耗媒质中均匀平面波的区别 ❖ 掌握集肤效应、趋肤深度、表面电阻的定义
6.2 导电媒质中的平面电磁波
6.2.1导电媒质中平面电磁波的传播特性
1. 复介电常数
无源、无界的导电媒质中麦克斯韦方程的复数形式为
g
g
g
H E j E
Eoe
E0
1 e
1
1
2
1
2
1
良导体
2 1 πf
上式表明,频率越高或媒质的导电能力越强,趋肤深度δ就越小。
E0e jt
O
x
E0e ze jt
z
良导体时, 而 2π 以及 1 ,则良导体中的趋肤深度
E
uuv ey
1 j
Ex z
将(3)式代入上式得
g uuv H ey 其瞬时值形式为
g
E m
e ze j z
j
uuv uuv H ey
Em
ez cos(t z 0 )
j
(4) (4)
2 传播常数γ
E0e jt
x
O
由于
2
2c
2 (
j )
j
E0e ze jt
联立可得
2
1
2
1
2
1
2
1
可见,传播常数γ的
实部β决定相位变化
量,虚部z α决定幅度
变化量。
由(3)、(4)式可知,导电媒质中电场和磁场的振幅均按e-αz随
传播距离衰减,每传播单位长度(z=1)振幅衰减为原来的e-α倍,故
α称为衰减常数,另外β表示相位随传播距离的变化量,故β称为相位
t
传导电流越大,损耗越大,定义导电媒质的损耗角 c 。
tg c
可见,损耗角与频率、媒质参数有关。
根据损耗角可将导电媒质分为弱导电媒质(电介质)、强导电媒质 (良导体)和一般的导电媒质(不良导体)。
6.2.2 趋肤深度和表面电阻
1. 电介质中的均匀平面波
对于电介质:
tg
c
=
1
物理意义表示电介质中的传导电流远小于位移电流,相关参数有:
g
g
2 E 2 E 0
g
g
2 H 2 H 0
(1)传播常数 (2)
对于均匀平面电磁波,设沿z轴传播,电场强度只有x分量,则由上节
可计算出式(1)的解为:
用γ替代无耗 媒质解中的k
g
2 Ex z 2
2
g
Ex
0
g
g
g
Ex Em e j z Em e j z
对于沿z轴正方向传播的均匀平面波,其解为:
c
e ze j ze j
其瞬时值为
uuv H
uuv ey
Em c
e z
cos(t
z
0 )
1 arctg 2
可知,σ愈大,则θ愈大,表示磁场强度比电场强度的相位滞后越 多,尽管电场与磁场有相位差,但二者仍然保持互相垂直,且都垂直于 传播方向。
4. 相速度和波长
导电媒质中均匀平面波的相速为
波长为
(3)c 表明导电媒质中电场和磁场的相位不同,出现相位差。
(4)导电媒质中电磁波的相速度不再是常数,而是随频率变化的函数,有 色散现象。
(5)导电媒质中平均磁场能量密度 wav,m 大于平均电场能量密度 wav,e 。
6. 损耗角
复介电常数
c
1
j
j
虚部与实部之比为
g
E E
J
g
D
传导电流 位移电流
g
g
Ex Em e j z
其中
g
Em Eme j0
设 j
g
g
g
则
Ex
E e j( -j )z m
Em e ze j z
(3)
uv
uuv
uuv
其瞬时值为 E z,t exEx z,t exEmez cos(t z 0) (3)
g
g
由方程 E j H得
g
g
H
1 j
g
定义
j
1
j
g
E
g
jc E
c
1
j
j
导电媒质的等效 复介电常数
引入εc后方程形式与无耗媒质中麦克斯韦方程具有完全相同的形式,
可将导电媒质看做具有复介电常数εc的介质。
这样可得到E、H满足的亥姆霍兹方程(即复数波动方程)为
g
g
2 E 2c E 0
g
g
2 H 2c H 0
令 2 2c
Ex2
1 2
c
Ex2
1 2
Ex2
j
1 2
Ex2
1
2
we
1
2
we
可见,导电媒质中 wm we ,其波阻抗呈电阻、电感性质。
从以上分析可以看到,导电媒质中的平面波与理想介质中的平面波 相比具有以下特点: (1)导电媒质中的电磁波是衰减波,频率越高或电导率越大,α就越大, 衰减也就越快。 (2)导电媒质中平面波的波阻抗c 为复数,呈现电阻、电感特性。
象称为色散。
5. 电场能量和磁场能量
在理想介质中,电场与磁场能量密度是相等的,即
2
we
1 2
Ex2
1 2
Hy
2
1 2
H
2 y
1 2
H
2 y
wm
由上式表明,理想介质中波阻抗为纯阻,电场与磁场相位相同,而导
电媒质下:
we
1 2
Ex2
wm
1 2
H
2 y
1 2
Ex c
2
1 2
c
2
