8土力学2 第八章 土坡稳定分析521
大学土力学PPT教学课件 第八章 边坡稳定分析
R b
6
7 C
A
2 1 -2 -1 0
3
一个简化解决方法是将 滑动土体分成条—条分 法。
山东交通学院交通土建工程学院
《土质与土力学》
2．条分法中的力和求解条件 未知量数目：
• • • Wi大小和方向已知； 滑动面上的 Ni 、 Ti( 含 cili 和 Nitgφ i)大小未知； 土条两侧，Ei 、 Fi 、 hi由前 一个土条计算得出,Ei＋1、 Fi＋1 、hi＋1未知； 可见，作用在土条上的作用力 有 5 个未知数，可以建立 3 个 平衡方程，故为静不定问题。
五、泰勒分析计算方法
泰勒提出在土坡稳定分析中共有5个计算参数，即土的容重γ、 土坡高度H、坡角β以及土的抗剪强度指标c、
若知道其中4个参数时就可以求出第五个参数值。为了简化 计算，泰勒把3个参数c、γ、H 组成一个新的参数Ns，称为 稳定因数，即
Ns
H
c1
山东交通学院交通土建工程学院
《土质与土力学》
W在滑动面AC上的切向分力及剪应力为：
T W sin T W sin 山东交通学院交通土建工程学院 AC AC
《土质与土力学》
土坡的稳定安全系数为： W cos tg f tg tg K AC W sin tg AC 当
时稳定安全系数最小，即土坡面上的一层土是最易滑动的。 因此，砂性土的土坡滑动稳定安全系数为：
试用泰勒方法分析计算：在坡脚下2.5m、0.75m、0.25m处有硬层 时，土坡稳定安全系数及圆弧滑动面的型式。
解：在坡脚下2.5m处有硬 层时，ndH=7.5m,则Nd=1.5， 查图可得：该滑动面为中 点圆。 同理可得0.75m处有硬 层·： Nd=1.15，滑动面 为坡脚圆，0.25m处有硬 层·： Nd=1.05，滑动面 为坡面圆
第八章+土坡稳定性分析
土力学与地基基础
• 由于计算上述安全系数时，滑动面为任意 假定，并不是最危险的滑动面，因此所求 结果并非最小的安全系数。通常在计算时 需要假定一系列滑动面，进行多次试算， 计算工作量很大。 • W.费伦纽斯（Fellenius,1927）通过大量计 算分析，提出了以下所介绍的确定最危险 滑动面圆心的经验方法。
土力学与地基基础
瑞典条分法和毕肖普法的比较
• 瑞典条分法忽略各条间力对Ni的影响，i土 条上只有Gi,Ni,Ti三种力作用，低估安全系 数5~20%。 • 毕肖普法忽略土条竖向剪切力的作用，考 虑了土条两侧的作用力，比瑞典条分法更 合理，低估安全系数约为2~7%。
土力学与地基基础
li
K
1 m cb Gi ui b X i tan i
G sin
i
i
土力学与地基基础
• 毕肖普条分法考虑了土条两侧的作用力， 计算结果比较合理。 • 分析时先后利用每一土条竖向力的平衡及 整个滑动土体的力矩平衡条件，避开了Ei 及其作用点的位置，并假定所有的 X i 均等 于零，使分析过程得到了简化。 • 但该方法同样不能满足所有的平衡条件， 还不是一个严格的方法，由此产生的误差 约为2%～7%。另外，毕肖普条分法也可以 用于总应力分析，即在上述公式中采用总 应力强度指标c、φ计算即可。
土力学与地基基础
土坡形态及各部分名称
坡肩 坡顶
坡高 坡脚
坡面
坡角
土力学与地基基础
土力学与地基基础
土力学与地基基础
土力学与地基基础
4.土坡由于其表面倾斜，在自重或外部荷 载的作用下，存在着向下移动的趋势， 一旦潜在滑动面上的剪应力超过了该面 上的抗剪强度，稳定平衡遭到破坏, 就可 能造成土坡中一部分土体相对于另一部 分的向下滑动，该滑动现象称为滑坡。 5.天然的斜坡、填筑的堤坝以及基坑放坡 开挖等问题，都要演算土坡的稳定性。 亦即比较可能滑动面上的剪应力与抗剪 强度，这种工作称为稳定性分析。
土力学第八章 土坡稳定分析
பைடு நூலகம்坡堆积区
易贡巨型高速滑坡及堰塞湖平面示意图
城市中的滑坡问题（香港，重庆）
挖 方
填 方
模型试验中直立边坡的破坏
滑坡原因
1）振动：地震、爆破
2）土中水位升、降
3）降雨引起渗流、软化
4）水流冲刷：使坡脚变陡
5）冻融：冻胀力及融化含水量升高
6）人工开挖：基坑、船闸、坝肩、隧洞出入口
滑坡形式
崩塌
平移
N
抗滑力 R W cos tg tg 滑动力 T W sin tg
tg Fs tg •当=时，Fs=1.0，天然休止角
•与所选的微单元大小无关 •坡内任一点或平行于坡的任一滑裂面 上安全系数Fs都相等
•安全系数与土容重无关
思考：在干坡及静水下坡中， 如不变，Fs有什么变化
0
注：（其中 n n l 是未知函数） 当=0（粘土不排水强度）时， c cu
M R cAcR 抗滑力矩 M R c Ac R (3) 安全系数： Fs 滑动力矩 M s Wd
O
讨论：
1 当 0 时，n 是 l(x,y) 的函数， 无法得到 Fs 的理论解 A
R
计算方法： 1 整体圆弧滑动法（瑞典Petterson） 2 瑞典条分法（瑞典Fellenius） 3 毕肖普法（ Bishop） 4 Janbu法 5 Spencer方法 6 Morgenstern-Price方法 7 陈祖煜的通用条分法 8 不平衡推力传递法 9 Sarma方法
1. 整体圆弧滑动法（瑞典圆弧法） 假设条件
整体对圆心的力矩平衡：
滑动力矩=抗滑力矩
i i i
Ms MR
土坡稳定分析ppt课件
陈祖煜(通用)条分法
陈祖煜对Morgentern法作了改进。 结合更一般工程实际，如地震力、坡面 载荷等，从土条的静力平衡得到的微分 方程出发，结合相应的边界条件，推导 出带有普遍意义的极限平衡方程式
陈祖煜(通用)条分法
土坡与土条示意图
x y
坡面线y=z(x)
G
β
Δx
滑裂面y(x)
a
b
Y+ΔY
Z+ΔZ
摩根斯坦（Morgenstern－ Price ）法
根据安全系数的定义及摩尔—库伦准则 ， 同时引用关于孔隙应力比的定义，分别得 ：
dT 1c'dsxecdN 't g '
Fs
dUsudW sec
摩根斯坦（Morgenstern－ Price ）法
综合以上各式，消去dT及dN′，得到每 一土条满足力的平衡的微分方程为 ：
E ( y y t) ( d 2 ) y ( E d E ) ( y d ) ( y y t d y t) ( d 2 ) y
X d 2 ( X x d ) d 2 X U x ( y h ) ( d 2 ( y U d ) ( y U d ) ( y h d )h
摩根斯坦（Morgenstern－ Price ）法
c 已知：方程中的
dW dx
、dU
dx
以求出，同时土质指标
dy
及 dx 都可
、tg 及孔隙
、
压力比ru也是给定的 ；
未知：E′、X及函数y=y′t(x)，还有安全
系数Fs
摩根斯坦（Morgenstern－ Price ）法
土力学 第8章 土坡稳定分析
四、坡率法确定边坡坡度
谢
谢！
u
4) 振动：地震、爆破
土坡滑动的预防措施
（1）改善排水条件 （2）种植适当的植被，避免土壤侵蚀 （3）减轻土坡上部的重量，增加坡脚土体的 重量 （4）减小坡高或坡角 （5）避免在坡顶堆放荷载，避免人、畜对坡 面的践踏 （6）对陡坡采用一定的坡面或坡体保护措施 （7）修复坡顶裂缝 （8）危险评估和预警
第 8 章 土坡稳定分析
第八章 土坡稳定分析
一、概述
二、无黏性土土坡的稳定性分析 三、黏性土土坡的稳定性分析 四、坡率法确定边坡坡度
一. 概述
1、土坡：是指具有一定倾斜坡面的土体。
各部分名称 坡肩 坡 高 坡趾 坡角 坡顶
一. 概述
2、分类：
天然土坡 人工土坡 天然土坡：是指自然界在成土过程中形成的山坡和河道岸 坡。多存在于山区或丘陵地区。
地震引发的滑坡
暴雨与地震引发泥石流-菲律宾
2006年2月17日菲律宾中东部莱特省因连日暴雨和南部 地区里氏2.6级轻微地震，爆发泥石流致近3000人遇难
云南徐村水电站溢洪道土坡滑坡－开挖
江岸崩塌滑坡－渗流
三峡库区滑坡问题－蓄水造成的滑坡
2001年，重庆市云阳县发生两次大型滑坡，其中武隆边坡失稳 造成79人死亡。国务院拨款40亿元用于三峡库区地质灾害治理
《建筑边坡工程技术规范》(GB50330-2013)规定：
如何分析、判断？
无黏性土土坡—相对简单 黏性土土坡—复杂
二、无黏性土土坡的稳定性分析
右下图表示坡角为β的无黏性土土坡，不考虑 渗流的影响。 纯净的干砂颗粒间无黏聚力c，其抗剪强度只有 摩擦力(内摩擦角φ )，颗粒的自重W在垂直和平行于 坡面方向的分力分别为
土力学 第八章
Fs
Mf M
(c l W cos tan ) W sin
i i i i i i
名词解释
天然休止角，土坡稳定安全系数，圆弧滑动法
简答题 1. 有渗流时对无粘性土坡的稳定性安全系数有何 影响？ 2. 简述瑞典圆弧滑动法计算的基本原理 简单计算题 一无粘性土坡，坡角β=23°，水流沿着坡而下， 则坡面土体中的动水力是多少？（3.9kN/m3）
多项选择题 以下是针对瑞典条分法的描述，正确的是 A.对每一土条力的平衡条件是不满足的 B.对每一土条本身的力矩平衡不满足 C.能满足整个滑动土体的整体力矩平衡 D.对每一土条力的平衡条件和力矩平衡条件都能 满足
有渗流 sin L 滑动力
T
β β N
G
T V sat sin
T G sin J G sin wiV 抗滑力 V sin wV sin T’=N tanφ=Vγ’ tanφ cosβ T V tan cos tan Ks T V sat sin sat tan 1 t an Ks 2 t an 由于 / 1 / 2
sat
二、粘性土坡的稳定性分析 1. 条分法的基本概念 ◆假定一个圆弧滑动面 分为若干土条 ◆对每个土条受力分析
6 7
5 3 2 1
4
◆求出在极限平衡状态下土坡稳定安全系数 ◆改变圆弧半径或圆形位置，重复上述过程。 →其中最小的安全系 Kf min数对应最危险滑动面 Kf min>1 稳定
2. 瑞典圆弧滑动法（瑞典条分法） i 7 6 ■假定条块两侧的作用力大小相等 i 方向相反且左右在同一条直线上。 4 3 ■安全系数定义为每一土条在滑动 2 面上所能提供的抗滑力矩之和与外 1 Ti 荷载及滑动土体自重在滑裂面上所 Ni 产生的滑动力矩之和的比值。 Wi Ti R RWi sin i 滑动力矩 Ni Wi cos i 抗滑力矩
土力学第8章土坡稳定性
渗流方向为顺坡时，渗透力合力为D：
D JAw wiAw O
•土坡的安全系数为： R
K
1 mi
[cb
(Wi
uib)
tan ]
Wi
sin i
r R
D
C
BA W
gD
Page7.swf
第四节 地基的稳定性分析
一、基础连同地基一起滑动
O
K M R 1.2
要求Fs ≥1.1～1.5。
由此可得如下结论：
当α＝φ时， Fs＝1，土坡处于极限稳定 状态，此时的坡角α为自然休止角；
无粘性土坡的稳定性与坡高无关，仅取
决于坡角α，当α＜φ时， Fs＞1，土坡
稳定。 二、有渗流作用的无粘性土坡
有渗流作用的无粘性土坡，因受到渗透 水流的作用，滑动力加大，抗滑力减小。
Fs i1
n
Wi sini
i 1
毕肖甫条分法详见P215～218。 最危险滑动面的确定方法详见P218～219。
五、图表法（稳定数法）
1、稳定数Ns
式中：
Ns
c
H
c－土的粘聚力（kPa）；
γ－土的重度（kN/m3）；
H－土坡的高度（m）。
2、内摩擦角、稳定数与坡角的关系 曲线（图8－15）。
渗流方向为顺坡时，渗透力为：J i w
•对水下的单元土体，W＝γ′，故土坡的
安全系数为： R cos tan
Fs T J ( w ) sin
JR
tan sat tan
T
N
αw
上式说明，渗流方向为顺坡时，无粘性 土坡的稳定系数与干坡相比，将降低 γ′/γsat倍，大约
第八章-土坡稳定性分析(改)
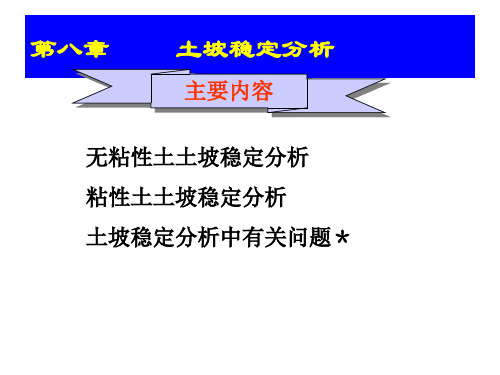
W
cu L R Fs Wd
d
O B A C W
粘性土土坡滑动前，坡 顶常常出现竖向裂缝
A
z0
深度近似采 用土压力临 界深度
z 0 2c / K a
裂缝的出现将使滑弧长度由 AC减小到AC，如果裂缝中 积水，还要考虑静水压力对 土坡稳定的不利影响
Fs是任意假定某个滑动面 的抗滑安全系数，实际要 求的是与最危险滑动面相 对应的最小安全系数
由于极限平衡法具有模型简单、计算公式简 捷、可以解决各种复杂剖面形状、能考虑各种 加载形式的优点,因此得到广泛的应用。 但是极限平衡法存在着一定的局限性: 其一,需要事先假设边坡中存在的滑动面(圆 弧法或折线法); 其二,无法考虑土体与支护结构之间的作用及 其变形协调关系; 其三,不能计算边坡及支护结构的位移情况。
三、毕肖普法(1955)
毕肖普法提出的土坡稳定系数的含义是整 个滑动面上土的抗剪强度τf与实际产生剪应力τ 的比，即K= τf/ τ， 假定滑动面是圆弧，任一土条i受力为：土 条重Wi引起的切向力Ti和法向力Ni，并分别作 用于底面中心处；土条侧面作用法向力 Ei 、 Ei+1 和切向力Xi、 Xi+1。但是毕肖普忽略了条间 切向力，即Xi+1-Xi =0，这样就得出了国内外广 泛使用的毕肖普简化公式：
1 [ci' bi (Wi ui bi )tgi' ] m i 简化后得： K Wi sin i
力矩分析 为什么没 考虑条间 力?
tgi' mi cos i sin i K
土坡稳定分析中有关问题＊
一、土的抗剪强度指标及安全系数的选用
* 指标值过高，有发生滑坡的可能
一、土坡圆弧滑动面的整体稳定分析 假定滑动面为圆柱面， 截面为圆弧，利用土 体极限平衡条件下的 受力情况： Mf f LR f LR Fs M LR Wd 饱和粘土，不排水 剪条件下，u＝0， τf ＝cu 滑动面上的最 大抗滑力矩与 滑动力矩之比
岩土力学教案第8章
第八章土坡稳定性分析§8.1 概述一、土坡原因在于土体内的剪应力在某时刻大于土的抗剪强度。
土中剪应力和土体的抗剪强度随时间是变化的。
1．促使剪应力增加的原因有：172（1）土坡变陡；（2）渗透水流的动水压力过大；（3）坡顶有超载作用；（4）打桩、爆破、地震、火车、汽车等动荷载作用均会增加剪应力。
2．造成土抗剪强度降低的原因有：（1）冻胀再融化；（2）振动液化；（3）浸水后土的结构崩解；（4）土中含水量增加等。
土坡失稳一般多发生在雨天，因为水渗入土中一方面使土中剪应力增加了；另一方面又使土的抗剪强度降低了，特别是坡顶出现竖向大裂缝时，水进入竖向裂缝对土坡产生侧向压力，从而导致土坡失稳。
因此，土坡产生竖向裂缝常常是土坡失稳的预兆之一。
四、影响土坡稳定性的主要因素（1）边坡坡角β。
坡角β越小愈安全，但是采用较小的坡角β，在工程中会增加挖填方量，不经济。
（2）坡高H。
H越大越不安全。
（3）土的性质。
γ、ϕ和c大的土坡比γ、ϕ和c小的土坡更安全。
（4）地下水的渗透力。
当边坡中有地下水渗透时，渗透力与滑动方向相反时，土坡则更安全；如两者方向相同时，土坡稳定性就会下降。
（5）震动作用的影响。
如地震、工程爆破、车辆震动等。
173174（6）人类活动和生态环境的影响。
§8.2 无粘性土坡稳定分析由粗颗粒土（c =0）所堆筑的土坡称为无粘性土坡。
无粘性土坡的稳定分析比较简单，下面分两种情况进行讨论。
一、无渗流作用时的无粘性土坡在分析无粘性土的土坡稳定时，根据实际观测结果，通常均假设滑动面为平面。
上图为一简单土坡，土坡高为H ，坡角为β，土的重度为γ，土的抗剪强度ϕστtan =f 。
若假定滑动面是通过坡角A 的平面AC ，AC 的倾角为α，并沿土坡长度方向截取单位长度进行分析，则其滑动土楔体ABC 的重力为：()ABC W ∆⨯=γ则沿滑动面向下的滑动力为：αsin W T =抗滑力为摩擦力，即：tan cos tan T N W ϕαϕ'==土坡滑动稳定安全系数为：αϕαϕαtan tan sin tan cos =='==W W T T F s 滑动力抗滑力175当βα=时，滑动稳定安全系数最小，即βϕtan tan min =S F 由上式可得如下结论：（1）当坡角ϕβ=，S 1F =，即土坡处于极限平衡状态，此时β称为天然休止角；（2）只要坡角ϕβ<（S 1F >），土坡就稳定，而且与坡高无关； （3）为了保证土坡有足够的安全储备，一般要求S 1.3~1.5F >。
土坡稳定分析概述
土坡稳定分析概述自然环境的影响对地表构成的坡体，工程活动的需要形成的边坡，在内因条件和外因条件的共同影响下，使得坡体在一定的应力和土体强度条件下保持着平衡稳定，当稳定所对应的外部条件发生了改变时，其所对应的应力状态也将发生改变，当应力的改变并同时影响着坡面土体强度变化或超出了坡体强度所对应的范围后，旧的平衡被打破，新的平衡必将去取代原有的平衡状态，因此出现了滑坡。
为了对坡体进行安全性评价，就建立了各种土坡稳定分析的方法和评价机制。
值得注意的是，工程中的坡体稳定分析的方法大都建立在使用静态参数的基础上，稳定分析计算的结果是使用安全系数去度量的，因而计算的结果是静态的反映。
然而，土坡的安全性却是相对是动态的、变化的，应当建立与其动态相适应的评价机制，可以这样说，对于土坡的真正安全可靠性评价还没有实现。
目前在工程应用实际中，评价坡体稳定的方法依然是安全系数的度量——相对是静态的方法。
从十九世纪二十年代所提出的瑞典圆弧分析法，到当前各类的数值计算方法，应用土体的强度参数大多在某一确定强度条件下，建立坡体稳定分析的方法，求得土坡稳定的安全系数评价，并作为工程具体应用的依据。
分析土坡稳定所采用的具体计算方法时，一般将土坡安全系数Fs定义为抗滑力矩和滑动力矩之比或抗剪强度（能力）和剪应力（能力）之比，通常假定不同的滑裂面，求得不同的安全系数，经试算得到最小的安全系数值，作为土坡稳定的安全系数和相应的滑裂面。
而采用的分条——将假设滑动土体划分为土条作为分析单元——从单元土条受力角度出发，考虑其边界受力条件，寻求必要的平衡方程，经过假定条件处理，以减少待定的未知量，应用极限平衡的原理，建立坡体整体评价的安全系数的过程计算方法成为不少学者致力改进的方向，为土坡坡体稳定分析建立评价的具体参数。
土坡稳定分析的研究发展大体分为：在十九世纪六十年代以前，以减少计算工作量、寻找滑动中心和滑裂面的规律是研究的主要目标；随着计算技术和计算机的出现和应用，对基本假定进行修改和补充、使之更符合实际的普遍条分法并借和计算机程序设计提出新的分析方法数值计算的现代阶段。
土力学第八章土坡稳定分析
• 8.2.6 各种土坡稳定分析方法比较
• 圆弧滑动法是目前工程实践中分析黏性土坡稳定性广 泛使用的方法。这个方法把滑动面简单地当作是圆弧， 有的认为滑动土体是刚性体，没有考虑分条之间的推力， 或是只考虑分条间的水平推力。总之，条分法计算的结 果，虽不能完全符合实际，但由于其计算概念简明，且 能分析复杂条件下土坡的稳定性，所以，在各国工程实 践中普遍使用，并积累了比较丰富的经验。经验证明， 由均质黏性土组成的边坡，其真正最危险滑动面形状接 近圆弧。同时在最危险滑动面附近的滑弧，其安全系数 变化很小，因而可以采用瑞典公式或毕肖普公式计算。 有研究指出，毕肖普简化法的滑动面较平缓，符合一般 危险滑动位置。因此，毕肖普简化法较为合理。
【解】三相草图求土的饱和容重
：
sa t 2 .6 5 1 (1 e 0 .2 ) 9 .8 2 0 .4 k N /m 3
土的浮重度： s a w t( 2 . 4 9 . 0 8 ) k / m 3 N 1 . 6 k / 0 m 3 N
渗透坡降：i h sbb/tcao nssin
【例8.1】如图8.7所示，一无限长土坡与水平面成α角，土 的容重γ=19.0kN/m³，土与基岩面的抗剪强度指标c=0， =30°。求安全系数Fs=1.2时的α角的容许值。
【解】从无限长土坡中截取单宽土柱进行稳 定分析，单宽土柱的安全系数与全坡相同。
土柱重量：WH
沿基面滑动力：T W sin
沿基面抗滑力：
•安全系数与土容重无关
•与所选的微单元大小无关
•坡内任一点或平行于坡的任一滑
裂面安全系数Fs都相等
思考：在干坡及静水下坡中，
如不变，Fs有什么变化?
• 8.1.2 有渗透水流的均质土坡 降雨
土力学_第8章(土坡稳定性分析)
单元受力分析
抗滑力
Ff=FNtan=Fwcostan
9
土坡稳定系数
定义：抗滑力（Ff）与下滑力（F）之比。
Fs
Ff F
Fw cos tan tan Fw sin tan
自然休止角或安息 角
讨论：
（2）当 时，即：Fs>l，土坡处于稳定状态；
N i'
T fi
fili
Fs
cili tani N i Fs Fs
c' l 1 (Wi X i ui li cos i i i sin i ) mi Fs
mi cos i (1 tani tan i ) Fs
20
然后就整个滑动土体对圆心O求力矩平衡，此时相邻土条之间侧壁作用力的 力矩将相互抵消，而各土条的Ni及uili的作用线均通过圆心，故有：
（2）对已有边坡的稳定性进行评价。（如：地质灾害评估）
在工程实践中，土坡稳定性分析方法主要有：
（1）极限平衡法；（2）数值分析方法；（3）概率分析方法
8
二、无粘性土土坡稳定分析
由粗粒土所堆筑的土坡称为无粘性土坡 （1） 无渗透力作用（全干或全部淹没的土坡）
海底边 坡
自重：Fw 下滑力： F=Fwsin
Wi cos i tan i ci ) (li 1.0) R R(Wi cos i tan i ci li ) li n (Wi cos i t ani li ci ) Mr 整个土坡相应于滑动面AD的稳定性系数为： Fs i 1 n Ms Wi sin i 17 M r i Si R (
切坡、地下水活动或地震等因素的影响，使部分土体或岩体在重力作用 下，沿一定的软弱面或带、整体、缓慢、间歇性、以水平位移为主的变
土坡稳定分析
第八章土坡稳定分析学习指导内容简介土坡的稳定性分析是土力学中重要的稳定分析问题，本章将分别介绍无粘性土坡和粘性土坡的稳定性分析方法，讨论土坡最危险滑裂面的确定方法和土坡稳定分析的图解法，并将简单介绍天然土体上的土坡稳定分析方法。
教学目标重点学习粘性土坡的稳定性分析方法，掌握无粘性土坡和自然土坡的稳定分析方法。
学习要求1、了解无粘性土坡的稳定分析方法2、掌握粘性土坡的稳定分析方法，包括整体圆弧滑动法和条分法（瑞典条分法、毕肖甫法和普遍条分法）；3、掌握粘性土坡最危险滑裂面的确定方法；了解粘性边坡稳定分析的图解法。
4、了解天然土体(裂隙硬粘土和软土地基）上的土坡稳定分析。
基本概念天然土坡、人工土坡、滑坡、圆弧滑动法、条分法、最危险滑动面学习内容第一节概述第二节无粘性土坡稳定分析第三节粘性土坡稳定分析第四节天然土坡的稳定分析第五节复合滑动面的土坡稳定分析第六节土坡稳定分析中的几个问题学时安排本章总学时数：5.5学时第一节 0.5学时第二节 0.5学时第三节 3学时第四节 0.5学时第五节 0.5学时第六节 0.5学时主要内容第一节概述本章主要学习目前常用的土坡稳定分析方法，学习与土的抗剪强度有关的问题。
无粘性土坡稳定分析分两种情况下(全干或全淹没情况、有渗透情况)无粘性土坡稳定分析方法，要求掌握无粘性土坡稳定安全系数的定义及推导过程，坡面有顺坡渗流作用下与全干或全淹没情况相比无粘性土土坡的稳定安全系数有何联系。
粘性土坡的稳定分析：学习其整体圆弧法、瑞典条分法、毕肖甫法、普遍条分法、有限元法等方法在粘性土稳定分析中的应用。
要求掌握圆弧法进行土坡稳定分析及几种特殊条件下土坡稳定分析计算。
边坡稳定分析的总应力法和有效应力法：学习稳定渗流期、施工期、地震期边坡稳定分析方法。
土坡稳定分析讨论三个问题：土坡稳定分析中计算方法问题、强度指标的选用问题和容许安全系数问题。
一、基本概念土坡就是具有倾斜坡面的土体。
由自然地质作用所形成的土坡，如山坡、江河的岸坡等，称为天然土坡(naturalsoilslope)。
(完整版)土坡稳定性分析
第七章土坡稳定性分析第一节概述土坡就是由土体构成、具有倾斜坡面的土体，它的简单外形如图7-1所示。
一般而言，土坡有两种类型。
由自然地质作用所形成的土坡称为天然土坡，如山坡、江河岸坡等；由人工开挖或回填而形成的土坡称为人工土(边)坡，如基坑、土坝、路堤等的边坡。
土坡在各种内力和外力的共同作用下，有可能产生剪图7-1 土坡各部位名称切破坏和土体的移动。
如果靠坡面处剪切破坏的面积很大，则将产生一部分土体相对于另一部分土体滑动的现象，称为滑坡。
土体的滑动一般系指土坡在一定范围内整体地沿某一滑动面向下和向外移动而丧失其稳定性。
除设计或施工不当可能导致土坡的失稳外，外界的不利因素影响也触发和加剧了土坡的失稳，一般有以下几种原因：1．土坡所受的作用力发生变化：例如，由于在土坡顶部堆放材料或建造建筑物而使坡顶受荷。
或由于打桩振动，车辆行驶、爆破、地震等引起的振动而改变了土坡原来的平衡状态；2．土体抗剪强度的降低：例如，土体中含水量或超静水压力的增加；3．静水压力的作用：例如，雨水或地面水流入土坡中的竖向裂缝，对土坡产生侧向压力，从而促进土坡产生滑动。
因此，粘性土坡发生裂缝常常是土坡稳定性的不利因素，也是滑坡的预兆之一。
在土木工程建筑中，如果土坡失去稳定造成塌方，不仅影响工程进度，有时还会危及人的生命安全，造成工程失事和巨大的经济损失。
因此，土坡稳定问题在工程设计和施工中应引起足够的重视。
天然的斜坡、填筑的堤坝以及基坑放坡开挖等问题，都要演算斜坡的稳定性，亦既比较可能滑动面上的剪应力与抗剪强度。
这种工作称为稳定性分析。
土坡稳定性分析是土力学中重要的稳定分析问题。
土坡失稳的类型比较复杂，大多是土体的塑性破坏。
而土体塑性破坏的分析方法有极限平衡法、极限分析法和有限元法等。
在边坡稳定性分析中，极限分析法和有限元法都还不够成熟。
因此，目前工程实践中基本上都是采用极限平衡法。
极限平衡方法分析的一般步骤是：假定斜坡破坏是沿着土体内某一确定的滑裂面滑动，根据滑裂土体的静力平衡条件和莫尔—库伦强度理论，可以计算出沿该滑裂面滑动的可能性，即土坡稳定安全系数的大小或破坏概率的高低，然后，再系统地选取许多个可能的滑动面，用同样的方法计算其稳定安全系数或破坏概率。
土力学电子教案之土坡稳定分析
教案表头：教学内容设计及安排第八章土坡稳定分析第一节无粘性土坡的稳定分析【基本内容】天然土坡：由于地质作用而自然形成的土坡。
人工土坡：人们在修建各种工程时，在天然土体中开挖或填筑而成的土坡。
滑坡：土坡丧失其原有稳定性，一部分土体相对另一部分土体滑动的现象。
分析土坡稳定性的目的：验算土坡的断面是否稳定合理，或根据土坡预定高度、土的性 质等已知条件，设计出合理的土坡断面。
简单土坡：土坡的坡顶和底面都是水平面，并伸至无穷远，土坡由均质土组成。
一、一般情况下的无粘性土土坡条件：均质的无粘性土土坡，干燥或完全浸水，土粒间无粘结力分析方法：只要位于坡面上的土单元体能够保持稳定，则整个坡面就是稳定的 滑动力： T =W sin β 垂直于坡面上的分力： N = W cos β最大静摩擦力： T '= N tan ϕ = W cos βtan ϕ 抗滑力与滑动力的比值称为稳定安全系数K ，2K =βϕβϕβtan tan sin tan cos =='W W T T当β=ϕ 时，K =1，土坡处于极限平衡状态。
砂土的内摩擦角也称为自然休止角。
当β＜φ，即K ＞1，土坡就是稳定的。
可取K =1.1~1.5。
【讨论】无粘性土土坡的稳定性与坡高无关，仅取决于坡角β。
二、有渗流作用时的无粘性土土坡分析方法：若渗流为顺坡出流，则渗流方向与坡面平行，此时使土体下滑的剪切力为J W J T +=+βsin 稳定安全系数为JW W JT T F f s +=+=βϕβsin tan cos 对单位土体，土体自重W =γ '，渗透力J =γw i ，水力坡降i =sin β，于是βγϕγβγβγϕβγtan tan sin sin tan cos sat w s F '=+''==【讨论】当坡面有顺坡渗流作用时，无粘性土土坡的稳定安全系数将近乎降低一半。
【例题先自习后讲解】【例8-1】有一均质无粘性土土坡，其饱和重度 γsat =20.0kN/m 3, 内摩擦角ϕ =30°, 若要求该土坡的稳定安全系数为1.20，试问在干坡或完全浸水情况下以及坡面有顺坡渗流时其坡角应为多少度？ 【讨论】有渗流作用的土坡稳定比无渗流作用的土坡稳定，坡角要小得多。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
M R cAcR 抗滑力矩 M R cu Ac R (3) 安全系数： Fs 滑动力矩 M s Wd
8.3 粘性土坡的稳定分析
一、 整体圆弧滑动法
O d R B
讨论：
1 当 0 时，n 是 l(x,y) 的函数， 无法得到 Fs 的理论解 A
C
W
2 其中圆心 O 及半径 R 是任意假设的，并不是最危险 滑动面，还必须试算若干个滑动面，找到最小安全系数
K=Hmax/H （3）已知、H、、 求c1 c1 K=c/c1
一、 整体圆弧滑动法 8.3 粘性土坡的稳定分析 3 泰勒分析方法（Tayler 稳定数法确定Ks） 应用
稳定因数： N s
H
c
解：由法（3）知 K=c/c1
19.4 8 c1 16.9kPa Ns 9.2
8.3 粘性土坡的稳定分析
∑Fz=0
Wi Hi Ni cosi Ti sin i
Pi hi H i
四、杨布条分法
Hi+1 Pi+1 Wi Ti Ni hi+1
∑Fx=0 Pi Ti cosi Ni sin i
c l Ni tgi 极限平 Ti i i 衡条件 Fs
瑞典条分法（费伦纽斯/简单条分法）
Ei hi X i
i
未知数: 5 方程数: 3 属于二次静不定问题 瑞典条分法假定： 圆弧滑裂面；不考虑条间力
忽略所有条间作用力：Ei、Xi=0 假定Ni、Ti作用于条块底面中点
8.3 粘性土坡的稳定分析 径向力平衡：
Ni Wi cosi
二、瑞典条分法 O R C
H
c 25 K 1.48 c1 16.9
8.3 粘性土坡的稳定分析 条分法的基本原理及分析
二、瑞典条分法
源起
整体圆弧法 ： 0 ntg dl n 是 l(x,y) 的函数
L
O
O
i
R
思路
R b B B C 7
C
离散化
分条
A
5 W 4 d 3 A 1 2 -1 -2 0
Wi Ti
hi+1
i
Ni
假定： 圆弧滑裂面；忽略条间力切向力
忽略条间切向力：Xi- Xi+1=0 假定Ni、Ti作用于条块底面中点
8.3 粘性土坡的稳定分析
∑Fz=0 极限平 衡条件
Wi Ni cosi Ti sin i
ci li Ni tgi Ti Fs
方程组求解，得到：
Pn=0
需经过多次逼近迭代法求解Ks。
8.3 粘性土坡的稳定分析 几种方法总结
方法 滑裂面形状 假设 适用性 精度 整体力矩 整体圆弧法 简单条分法 圆弧 圆弧 毕肖普法 圆弧 简布法 任意
刚性滑动体 忽略全部条 忽略条间切向 力 滑动面上极 简力 限平衡
b B
3 4 5
6
7
Fs
(c l W cos tg ) W sin
i i i i i i i
A
变化圆心 O 和半径 R Fs 最小 END
Wi Ti
i
Ni
8.3 粘性土坡的稳定分析
毕肖普（Bishop）条分法 （圆弧滑动面）
三、毕肖普条分法
Xi+1 Ei+1
Ei
hi X i
• 江、河、湖、海岸坡
• 山、岭、丘、岗、天然坡
人工土坡
• 挖方：沟、渠、坑、池 • 填方：堤、坝、路基、堆料
8.1 概述
8.1 概述
城市中的滑坡问题（香港，重庆）
挖 方
填 方
8.1 概述
8.1 概述
土坡失稳形态 与当地工程地质条件有关。
8.1 概述
土坡稳定分析目的：检验所设计的土坡断面 是否安全合理。土坡稳定安全度用稳定安全系 数K表示，K=f/，即抗滑力与滑动力之比。
降雨
正常蓄水土坝下游
逸出段
水位骤降的土坝上游
8.2 无粘性土坡的稳定分析
有沿坡渗流情况
h i sin l
取微单元 A，以土骨架为隔离体：
(1) 自重： W V 渗透力： （方向：平行于土坡）
J jV i wV sin wV (2) 滑动力：
A
J l h W
N
T
T J （ sin w sin ）V sat sin V
(3) 抗滑力：
J W N
R
R Ntg V cos tg
(4) 抗滑安全系数：
R cos tg Fs tg T J sat sin sat tg
一、 整体圆弧滑动法 8.3 粘性土坡的稳定分析 泰勒图表法（Tayler 稳定因数法确定Ks）
稳定因数： N s
H
c
一、 整体圆弧滑动法 8.3 粘性土坡的稳定分析 3 泰勒分析方法（Tayler 稳定数法确定Ks）
应用 已知,c,,,H
k
稳定因数： N s
H
c
K=max/
M s Wd
R B
C
(2) 抗滑力矩：
M R f dl R
0 L L 0
A
d
W
L (c ntg )dl R cAc R ntgdl R
0
注：（其中 n n l 是未知函数） 当=0（粘土不排水强度）时， c cu
6
条分法
8.3 粘性土坡的稳定分析 安全系数定义
ci li Ni tgi Fs Ti Ti T fi
二、瑞典条分法
O
i 2 1 -1 -2 0
R b B 3 4 5
Ti Ni
C 6 7
ci li Ni tgi Ti Fs
A
8.3 粘性土坡的稳定分析
二、瑞典条分法
Xi+1 Ei+1 Wi Ti Ni hi+1
一、 整体圆弧滑动法 8.3 粘性土坡的稳定分析 泰勒图表法（Tayler 稳定因数法确定Ks）
土坡稳定性与、H、、c、等5个因素有关，知道其中任 意4个可求第5个。
为简化计算，提出一个新参数Ns，称为稳定因数，即：
Ns
H
c
经过大量计算，可得到Ns与、的关系曲线，见图8-10。
8.3 粘性土坡的稳定分析
一、 整体圆弧滑动法
1 整体圆弧滑动法（瑞典圆弧法） 假设条件
• 均质土 • 二维 • 圆弧滑动面
O R
均质简单土坡
• 滑动土体呈刚性转动
• 在滑动面上处于极限平衡条件
8.3 粘性土坡的稳定分析
一、 整体圆弧滑动法
O
平衡条件（各力对圆心O的力矩平衡）
(1) 滑动力矩：
——最危险滑动面
3 适用于饱和软粘土，即 =0 情况
8.3 粘性土坡的稳定分析
一、 整体圆弧滑动法
费伦纽斯法确定最危险滑动面圆心经验方法
1、2可根据坡度或坡角查表8-1。
8.3 粘性土坡的稳定分析
一、 整体圆弧滑动法
泰勒方法确定最危险滑动面圆心（根据、及硬层埋 置深度等因素提出，参见图8-8及8-9）。
《土力学2》之第八章
土坡稳定分析
8.1 概述 8.2 无粘性土坡的稳定分析 8.3 粘性土坡的稳定分析 8.4 土坡稳定分析中几个问题
8.1 概述 边坡稳定分析对象： 土石坝、库区边坡，堤坝填筑 土质、岩质边坡
土坡：具有倾斜面的土体
坡肩
坡顶
坡度：1:m
坡 高 坡趾 坡角
坡底
8.1 概述 天然土坡
Fs
(c l W cos tg ) W sin
i i i i i i i
Fs
Wi Ti
i
Ni
显式 表达
8.3 粘性土坡的稳定分析
圆心 O，半径 R（如图）
分条：b=R/10
二、瑞典条分法 O R C
计 算 步 骤
编号：过圆心垂 线为 0# 条中线
列表计算 li Wi i
i 2 1 -1 0 -2
8.2 无粘性土坡的稳定分析 讨论：
tg Fs sat tg
有沿坡渗流情况
A l
h
J
W’
N T’
• 0.5 与无渗流比较Fs减小近一倍 sat
意味着原来稳定的坡，有沿坡渗流时可能破坏
• 与容重有关 • 与所选V大小无关，亦即在这种坡中各点安全系数相同
8.3 粘性土坡的稳定分析 破坏特点
sin i tgi mi cos i Fs
A
隐式 表达
Ei+1 Wi Ti Ni hi+1
Ei hi
i
8.3 粘性土坡的稳定分析
圆心 O，半径 R 设 Fs=1.0
三、毕肖普条分法
O i 2 1 -1 -2 0
R b B 3 4 5 6
计 算 步 骤计算 miC 7Fs Fs
i
方程组求解 Ni Ti Pi
11 P1 = P1 10 P2 = P1 + P2 = P1 + P2 8 9 7 Pj = Pi ( i=1, j ) P0=0 6 5 12 3 4 Pn = Pi = 0 ( i=1, n )
与 Hi 有关，但 Hi 可 以通过每个土条的力 矩平衡由 hi 得到
•由于存在粘聚力C，与无粘性土坡不同； •其危险滑裂面位置在土坡深处； •对于均匀土坡，在平面应变条件下，其滑动面可用一圆 弧（圆柱面）近似。
8.3 粘性土坡的稳定分析 计算方法： 1 整体圆弧滑动法（瑞典Petterson） 2 瑞典条分法（瑞典Fellenius） 3 毕肖普法（ Bishop） 4 Janbu法 5 Spencer方法 6 Morgenstern-Price方法 7 陈祖煜的通用条分法 8 不平衡推力传递法 9 Sarma方法