第八章+土坡稳定性分析
第08章土坡稳定-精选
浸润线以下部分应考虑水的 浮力作用，采用浮重度，动 水可按下式计算:
JG D Aw I A
ΔA——浸润线以下部分面积， 即动水力作用区域的面积。
in
in
KMs Mi
R(tg Wi cosi c li)
i1 in
i1
R Wi sini rJ
i1
§ 8. 4 水对边坡稳定的影响
k O k kO O m i n 2 5k k 1 1m i2 n1 11 1 O O O O OO OOkO O Ek B B k m i n52kOOO555Okk64k5O55OO14kO5O4k54kO5OkA564OO4355OO114kk6O44454kOk13O125O4OO34kk1k354kO2433311kkO4O1k1kmk2311kOOk123mk22i2kO231i2kknkO1n11O21kOm2kk111O1kEi2m25k11E1Ein21O11En11kOkEE11E1k111E1E141
➢计算滑动力矩和稳定力矩:
M siT iRW iRsini
M r ifiliR ( W ic o sitg i c ili) R
➢计算土坡的稳定安全系数
•对于均质土坡 ci c i
in
K Ms Mi
R (Wi cositgi cili)
i1 in R Wi sini
i1
in
)
K
条分法对非均质土坡、土坡外形复杂、土坡部分 在水下情况均适用。
§ 8.3 粘性土土坡稳定分析
二、圆弧滑动面的整体稳定分析
1、分析计算方法
1）假设条件： • 均质土 • 二维 • 圆弧滑动面 • 滑动土体呈刚性转动 • 在滑动面上处于极限平衡状态
第八章 土坡稳定性分析与计算
O
R
Vi+1
MR
(c l N tan ) T R R
i i i i i
H
i
Wi
Ti
Fs
Ms MR
(c l N tan ) R W sin R
i i i i i i
O i 2 1 -1 -2 0
R b B 3 4 5 6
C
7
计 算 程 序 流 程
计算 mi
Fs Fs
计算
Fs
No
Fs Fs Fs
A
变化圆心 O 和半径 R
Fs 最小
END
3.简化毕肖普法的特点
★假设滑裂面为圆弧； ★假设条块间作用力只有法向力没有切向力 （Vi=0）； ★满足整体力矩平衡条件； ★满足各条块力的多边形闭合条件，但不满足条块的 力矩平衡条件； ★满足滑动面上的极限平衡条件。
i
f 土坡稳定 安全系数
(一) 瑞典条分法的基本原理
1、假设圆弧滑动面 确定圆心和半径
2、把滑动土体分成若干条（条分法） 3、取第i条土条进行受力分析
O
R
Vi+1 Hi hi Vi Wi Hi+1 hi+1
i
Ti Ni
瑞典条分法
静定化条件：假设条块两侧的作用 力合力Si，Si+1 大小相等、方向相 反且作用于同一直线上——不考虑 条块间的作用力。 1）根据径向力的静力平衡条件 得
表层滑动
砂土
概述 表层滑动的边 坡稳定分析
天然休止角
无粘性土
8土坡稳定分析
=0 F
s
β1 β
B
>0
圆心位置在EO
的延长线上
圆心位置由β1， β2确定
O β2 A
H 2H
4.5H
E
条分法分析步骤I
O
R
βi
d
c
i A
da b
c
Pi+1Xi+1
Wi
Xi
Pi
b
a Ti Ni
li
C B
H
假设两组合力 (Pi，Xi)＝ (Pi ＋1，Xi＋1)
静力平衡
1.按比例绘出土坡剖面
2.任选一圆心O，确定
四、安全系数的选用
影响安全系数的因素很多，如抗剪强度指标的选用，计算方 法和计算条件的选择等。工程等级愈高，所需要的安全系数愈大。
目前，对于土坡稳定的安全系数，各个部门有不同的规定。
同一边坡稳定分析，选用不同的试验方法、不同的稳定分析方法， 会得到不同的安全系数。根据结果综合分析安全系数，得到比较 可靠的结论
及土条重W i，计算该圆心和半径下的安全系数 ④对圆心O选不同半径，得到O对应的最小安全系数； ⑤在可能滑动范围内，选取其它圆心O1，O2，O3，…，重复
上述计算，求出最小安全系数，即为该土坡的稳定安全系数
四、泰勒图表法
土坡的稳定性相关因素：
泰勒（Taylor,D.W， 1937）用图表表达影 响因素的相互关系
其坡角应为多少度？ 干坡或完全浸水情况 T
顺坡出流情况 T
TN
W tan tan 0.481
Fs 25.7
JT N W
tan tan 0.241 sat Fs
13.5
渗流作用的土坡稳定比无渗流作 用的土坡稳定，坡角要小得多
第八章-粘性土土坡的稳定分析
泰勒图表法
• 计算简图：
泰勒图表法
• 计算简图：
条分法的基本概念
• 瑞典园弧法的局限： 1）对于外形比较复杂、0的粘性土坡，特别 是多层土坡； 2）滑动土体的重量和重心较难确定； 3）滑动面上的抗剪强度分布不均。 4）难以直接用瑞典圆弧法计算安全系数：
M R f LR Fs MS Wd
太沙基公式
• 基本假定： 1）土条两侧的推力Pi、Pi+1和摩擦力Hi、Hi+1的 合力大小相等、方向相反； 2）且它们的作用线重合。 • 受力分析： 1）土条的重力Wi 2）土条的径向反力Ni 3）侧向反力Ti
太沙基公式
• 抗转动稳定安全系数： 滑动力矩： 所有土条自重引起的切向力对园心的力矩。 抗滑力矩： 所有土条底部的抗剪强度对园心的力矩。 则抗转动稳定安全系数为抗滑力矩与滑动力矩之 比：
Qi是水平向惯性力； MiC是水平向惯性力对滑动圆心的力矩； ci、i是地震作用下土体的凝聚力和内摩擦角。
复合滑动面的土坡稳定分析
• 复合滑动面： 由直线和曲线组成的非圆弧滑动面。 • 非瑞典圆弧法概念： 简布非圆弧普遍条分法： 1）不是假定分条界面上推力的数值或方向； 2）而是假定推力作用点的位置； 3）按照静力平衡原理计算安全系数。
土坡最危险滑弧的确定
• 计算简图：
泰勒图表法
• 土坡稳定性的影响因素： c、、、、H • 稳定数： H c Ns c • 泰勒图表： 按不同的值绘出-Ns的关系曲线。 • 稳定性分析： 确定土坡的极限高度Hc或 极限坡脚。 • 适用条件： 泰勒图表法多用于计算均质、高度小于10m的堤 坝边坡。
简化毕肖普公式
• 抗转动稳定安全系数： 用总应力分析：
(ci li cos i Wi tgi ) sin i tgi ( cos i ) Fs Fs Wi sin i
土力学第8章土坡稳定性
渗流方向为顺坡时，渗透力合力为D：
D JAw wiAw O
•土坡的安全系数为： R
K
1 mi
[cb
(Wi
uib)
tan ]
Wi
sin i
r R
D
C
BA W
gD
Page7.swf
第四节 地基的稳定性分析
一、基础连同地基一起滑动
O
K M R 1.2
要求Fs ≥1.1～1.5。
由此可得如下结论：
当α＝φ时， Fs＝1，土坡处于极限稳定 状态，此时的坡角α为自然休止角；
无粘性土坡的稳定性与坡高无关，仅取
决于坡角α，当α＜φ时， Fs＞1，土坡
稳定。 二、有渗流作用的无粘性土坡
有渗流作用的无粘性土坡，因受到渗透 水流的作用，滑动力加大，抗滑力减小。
Fs i1
n
Wi sini
i 1
毕肖甫条分法详见P215～218。 最危险滑动面的确定方法详见P218～219。
五、图表法（稳定数法）
1、稳定数Ns
式中：
Ns
c
H
c－土的粘聚力（kPa）；
γ－土的重度（kN/m3）；
H－土坡的高度（m）。
2、内摩擦角、稳定数与坡角的关系 曲线（图8－15）。
渗流方向为顺坡时，渗透力为：J i w
•对水下的单元土体，W＝γ′，故土坡的
安全系数为： R cos tan
Fs T J ( w ) sin
JR
tan sat tan
T
N
αw
上式说明，渗流方向为顺坡时，无粘性 土坡的稳定系数与干坡相比，将降低 γ′/γsat倍，大约
第八章-土坡稳定性分析(改)
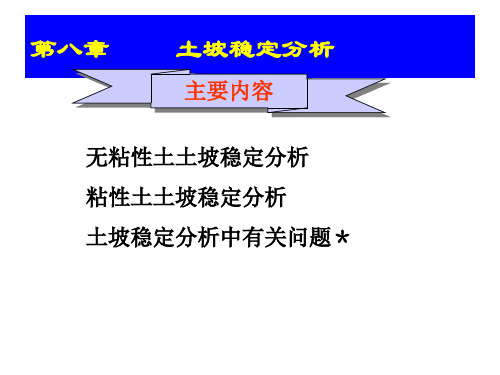
W
cu L R Fs Wd
d
O B A C W
粘性土土坡滑动前，坡 顶常常出现竖向裂缝
A
z0
深度近似采 用土压力临 界深度
z 0 2c / K a
裂缝的出现将使滑弧长度由 AC减小到AC，如果裂缝中 积水，还要考虑静水压力对 土坡稳定的不利影响
Fs是任意假定某个滑动面 的抗滑安全系数，实际要 求的是与最危险滑动面相 对应的最小安全系数
由于极限平衡法具有模型简单、计算公式简 捷、可以解决各种复杂剖面形状、能考虑各种 加载形式的优点,因此得到广泛的应用。 但是极限平衡法存在着一定的局限性: 其一,需要事先假设边坡中存在的滑动面(圆 弧法或折线法); 其二,无法考虑土体与支护结构之间的作用及 其变形协调关系; 其三,不能计算边坡及支护结构的位移情况。
三、毕肖普法(1955)
毕肖普法提出的土坡稳定系数的含义是整 个滑动面上土的抗剪强度τf与实际产生剪应力τ 的比，即K= τf/ τ， 假定滑动面是圆弧，任一土条i受力为：土 条重Wi引起的切向力Ti和法向力Ni，并分别作 用于底面中心处；土条侧面作用法向力 Ei 、 Ei+1 和切向力Xi、 Xi+1。但是毕肖普忽略了条间 切向力，即Xi+1-Xi =0，这样就得出了国内外广 泛使用的毕肖普简化公式：
1 [ci' bi (Wi ui bi )tgi' ] m i 简化后得： K Wi sin i
力矩分析 为什么没 考虑条间 力?
tgi' mi cos i sin i K
土坡稳定分析中有关问题＊
一、土的抗剪强度指标及安全系数的选用
* 指标值过高，有发生滑坡的可能
一、土坡圆弧滑动面的整体稳定分析 假定滑动面为圆柱面， 截面为圆弧，利用土 体极限平衡条件下的 受力情况： Mf f LR f LR Fs M LR Wd 饱和粘土，不排水 剪条件下，u＝0， τf ＝cu 滑动面上的最 大抗滑力矩与 滑动力矩之比
岩土力学教案第8章
第八章土坡稳定性分析§8.1 概述一、土坡原因在于土体内的剪应力在某时刻大于土的抗剪强度。
土中剪应力和土体的抗剪强度随时间是变化的。
1．促使剪应力增加的原因有：172（1）土坡变陡；（2）渗透水流的动水压力过大；（3）坡顶有超载作用；（4）打桩、爆破、地震、火车、汽车等动荷载作用均会增加剪应力。
2．造成土抗剪强度降低的原因有：（1）冻胀再融化；（2）振动液化；（3）浸水后土的结构崩解；（4）土中含水量增加等。
土坡失稳一般多发生在雨天，因为水渗入土中一方面使土中剪应力增加了；另一方面又使土的抗剪强度降低了，特别是坡顶出现竖向大裂缝时，水进入竖向裂缝对土坡产生侧向压力，从而导致土坡失稳。
因此，土坡产生竖向裂缝常常是土坡失稳的预兆之一。
四、影响土坡稳定性的主要因素（1）边坡坡角β。
坡角β越小愈安全，但是采用较小的坡角β，在工程中会增加挖填方量，不经济。
（2）坡高H。
H越大越不安全。
（3）土的性质。
γ、ϕ和c大的土坡比γ、ϕ和c小的土坡更安全。
（4）地下水的渗透力。
当边坡中有地下水渗透时，渗透力与滑动方向相反时，土坡则更安全；如两者方向相同时，土坡稳定性就会下降。
（5）震动作用的影响。
如地震、工程爆破、车辆震动等。
173174（6）人类活动和生态环境的影响。
§8.2 无粘性土坡稳定分析由粗颗粒土（c =0）所堆筑的土坡称为无粘性土坡。
无粘性土坡的稳定分析比较简单，下面分两种情况进行讨论。
一、无渗流作用时的无粘性土坡在分析无粘性土的土坡稳定时，根据实际观测结果，通常均假设滑动面为平面。
上图为一简单土坡，土坡高为H ，坡角为β，土的重度为γ，土的抗剪强度ϕστtan =f 。
若假定滑动面是通过坡角A 的平面AC ，AC 的倾角为α，并沿土坡长度方向截取单位长度进行分析，则其滑动土楔体ABC 的重力为：()ABC W ∆⨯=γ则沿滑动面向下的滑动力为：αsin W T =抗滑力为摩擦力，即：tan cos tan T N W ϕαϕ'==土坡滑动稳定安全系数为：αϕαϕαtan tan sin tan cos =='==W W T T F s 滑动力抗滑力175当βα=时，滑动稳定安全系数最小，即βϕtan tan min =S F 由上式可得如下结论：（1）当坡角ϕβ=，S 1F =，即土坡处于极限平衡状态，此时β称为天然休止角；（2）只要坡角ϕβ<（S 1F >），土坡就稳定，而且与坡高无关； （3）为了保证土坡有足够的安全储备，一般要求S 1.3~1.5F >。
土力学第八章土坡稳定分析
• 8.2.6 各种土坡稳定分析方法比较
• 圆弧滑动法是目前工程实践中分析黏性土坡稳定性广 泛使用的方法。这个方法把滑动面简单地当作是圆弧， 有的认为滑动土体是刚性体，没有考虑分条之间的推力， 或是只考虑分条间的水平推力。总之，条分法计算的结 果，虽不能完全符合实际，但由于其计算概念简明，且 能分析复杂条件下土坡的稳定性，所以，在各国工程实 践中普遍使用，并积累了比较丰富的经验。经验证明， 由均质黏性土组成的边坡，其真正最危险滑动面形状接 近圆弧。同时在最危险滑动面附近的滑弧，其安全系数 变化很小，因而可以采用瑞典公式或毕肖普公式计算。 有研究指出，毕肖普简化法的滑动面较平缓，符合一般 危险滑动位置。因此，毕肖普简化法较为合理。
【解】三相草图求土的饱和容重
：
sa t 2 .6 5 1 (1 e 0 .2 ) 9 .8 2 0 .4 k N /m 3
土的浮重度： s a w t( 2 . 4 9 . 0 8 ) k / m 3 N 1 . 6 k / 0 m 3 N
渗透坡降：i h sbb/tcao nssin
【例8.1】如图8.7所示，一无限长土坡与水平面成α角，土 的容重γ=19.0kN/m³，土与基岩面的抗剪强度指标c=0， =30°。求安全系数Fs=1.2时的α角的容许值。
【解】从无限长土坡中截取单宽土柱进行稳 定分析，单宽土柱的安全系数与全坡相同。
土柱重量：WH
沿基面滑动力：T W sin
沿基面抗滑力：
•安全系数与土容重无关
•与所选的微单元大小无关
•坡内任一点或平行于坡的任一滑
裂面安全系数Fs都相等
思考：在干坡及静水下坡中，
如不变，Fs有什么变化?
• 8.1.2 有渗透水流的均质土坡 降雨
土力学_第8章(土坡稳定性分析)
单元受力分析
抗滑力
Ff=FNtan=Fwcostan
9
土坡稳定系数
定义：抗滑力（Ff）与下滑力（F）之比。
Fs
Ff F
Fw cos tan tan Fw sin tan
自然休止角或安息 角
讨论：
（2）当 时，即：Fs>l，土坡处于稳定状态；
N i'
T fi
fili
Fs
cili tani N i Fs Fs
c' l 1 (Wi X i ui li cos i i i sin i ) mi Fs
mi cos i (1 tani tan i ) Fs
20
然后就整个滑动土体对圆心O求力矩平衡，此时相邻土条之间侧壁作用力的 力矩将相互抵消，而各土条的Ni及uili的作用线均通过圆心，故有：
（2）对已有边坡的稳定性进行评价。（如：地质灾害评估）
在工程实践中，土坡稳定性分析方法主要有：
（1）极限平衡法；（2）数值分析方法；（3）概率分析方法
8
二、无粘性土土坡稳定分析
由粗粒土所堆筑的土坡称为无粘性土坡 （1） 无渗透力作用（全干或全部淹没的土坡）
海底边 坡
自重：Fw 下滑力： F=Fwsin
Wi cos i tan i ci ) (li 1.0) R R(Wi cos i tan i ci li ) li n (Wi cos i t ani li ci ) Mr 整个土坡相应于滑动面AD的稳定性系数为： Fs i 1 n Ms Wi sin i 17 M r i Si R (
切坡、地下水活动或地震等因素的影响，使部分土体或岩体在重力作用 下，沿一定的软弱面或带、整体、缓慢、间歇性、以水平位移为主的变
第8章 土坡稳定性分析
土坡滑动失稳的原因 土坡滑动失稳的原因一般有以下两类情况： 土坡滑动失稳的原因一般有以下两类情况： 1.外界力的作用破坏了土体内原来的 外界力的作用破坏了土体内原来的应 1.外界力的作用破坏了土体内原来的应 力平衡状态。如基坑的开挖、路堤的填筑、 力平衡状态。如基坑的开挖、路堤的填筑、 土坡顶面上作用外荷载、土体内水的渗流、 土坡顶面上作用外荷载、土体内水的渗流、 地震力的作用等也都会破坏土体内原有的 应力平衡状态，导致土坡坍塌。 应力平衡状态，导致土坡坍塌。 2.土的抗剪强度由于受到外界各种因素 土的抗剪强度 2.土的抗剪强度由于受到外界各种因素 的影响而降低 促使土坡失稳破坏。 降低， 的影响而降低，促使土坡失稳破坏。如外 界气候等自然条件的变化、 界气候等自然条件的变化、土坡附近因打 桩、爆破或地震力的作用将引起土的液化 或触变，使土的强度降低。 或触变，使土的强度降低。
如果渗流逸出段顺坡面流动，则：
α =θ
i = dh / dl = sin α
[γ 'V cos α − γ wiV sin(α − θ )] tan ϕ γ 'V cos α tan ϕ Fs = = γ 'V sin α + γ wiV cos(α − θ ) γ 'V sin α + γ wV sin α
如上图所示的砂性土土坡，已知土坡高为H，坡角为β，土 如上图所示的砂性土土坡，已知土坡高为H 土的抗剪强度tf= 的重度为γ，土的抗剪强度tf=σtanϕ。若假定滑动面是通过坡 的平面AC，AC的倾角为 则可计算滑动土体ABC沿 脚A的平面AC，AC的倾角为α，则可计算滑动土体ABC沿AC 面上滑动的稳定安全系数K 面上滑动的稳定安全系数K值。 沿土坡长度方向截取单位长度土坡，作为平面应变问题分析。 沿土坡长度方向截取单位长度土坡，作为平面应变问题分析。 已知滑动土体ABC的重力为： 已知滑动土体ABC的重力为： W = γ × ( ∆ABC ) 的重力为 W在滑动面AC上的平均法向分力N及由此产生的抗滑力Tf为： 在滑动面AC上的平均法向分力 及由此产生的抗滑力Tf为 上的平均法向分力N
第八章土坡稳定分析
或用Ks表示
由此可见，对于均质无粘性土土坡，理论上只要坡角小于土 的内摩擦角，主体就是稳定的。Ks等于1时，主体处于极限平衡 状态，此时的坡角就等于无粘性土的内摩擦角。
二、有渗流作用时的无粘性土土坡
因此，当坡面有顺坡渗流作用时，无粘性土土坡的稳定安 全因数将近乎降低一半。
【例9-1】 均质无粘性土土坡，其饱和重度γsat=20.0 KN/m3， 内
（3）土的性质，如 、c和的值，如c、 值大，则土坡安全。
（4） 地下水的渗透力，当边坡中有地下水渗透时，渗透力与 滑动方向相反则安全，两者方向相同则危险。 （5）震动作用的影响如地震、工程爆破、车辆震动等。 （6）人类活动和生态环境的影响。
8.2 平面滑动面的土坡稳定分析
一、一般情况下的无粘性土土坡
摩擦角=300，若要求该土坡的稳定安全系数为，在干坡情况下以
及坡面有顺坡渗流时其坡角应为多少度？
8.3 瑞典条分法
粘性土由于土粒间存在粘聚力，发生滑坡是整体土体向下滑 动，坡面上任一单元的稳定条件不能用来代表整个土坡的稳定 条件。 粘性土土坡的滑动面在土坡内部。 通过对大量粘性土土坡的滑坡现场调查，发现滑坡面基本为 圆弧面，因此，假设粘性土土坡的滑动面形状为圆弧面。 粘性土坡稳定分析的方法主要是条分法。
①按比例绘出土坡，选择圆心，作 出相应的滑动圆弧，取圆心O，取半 径R； ②将滑动土体分成若干土条，对土 条编号；
③列表计算该圆心和半径下的安全 系数。
8.4 稳定数法
土坡的稳定性相关因素： 泰勒（，1937）用图
表表达影响因素的相 抗剪强度指标c和、
互关系
重度 、土坡的尺寸
Ns
Hcr
c
土坡的临界高 度或极限高度
第八章 土坡稳定
第八章土坡稳定(stability of Slopes)§ 8.1 概述结合工程实例，讲解土坡的概念及滑动面的形状。
土坡系指具有倾斜坡面的土体，如天然土坡及人工修建的土堤坝、公路铁路的路堤和路堑。
图8.1滑坡土坡受到各种自然因素或人为因素的作用时土坡土体会失去力学平衡，土坡就沿着其中某一滑面发生滑动，工程中称这一现象为滑坡(landslide)。
大量观察资料表明粘性土滑坡时滑动面(slip surface)近似于圆柱面，故在横断面上呈圆弧线；砂性土滑坡时滑动面近似于平面，故在横断面上呈直线。
滑坡的分析可按平面应变问题来处理。
12§ 8.2 直线滑面的土坡稳定验算适用范围：均匀的砂性土或成层的非均质砂性土构成的土坡；砂砾和卵石路堤或其它土坡；还有某些透水土虽有一定的粘聚力c ，但其抗剪强度主要由摩擦力部分提供者；皆可采用直线滑面法进行分析。
图8.2 平面滑坡βϕβsin tan cos '⋅⋅+⋅⋅==W L c W T T K 当c =0时，βϕβϕβtan tan sin tan cos =⋅⋅⋅=W W K为了确保土坡稳定性，必须使K > 1；铁路路基规范规定K= 1.05~1.25。
2§ 8.3 圆弧滑面的条分法分析从条分法的思想和基本原理出发，阐述滑坡的稳定性分析。
以耒宜高速公路郴州某一滑坡为例，结合自己的亲身体会，讲解增加土坡稳定性的措施。
粘性土坡滑动时，滑面接近为圆弧面；圆弧形滑面土坡稳定性分析方法有瑞典圆弧法(W.Fellenius ，1936)、毕肖普法(A.W.Bishop ，1995)(Bishop’s simplified method of slice)。
一、 瑞典圆弧滑面法(Swedish circle method)瑞典工程师W.Fellenius 提出的圆弧滑动面是稳定分析中的一种基本方法。
图8.3 瑞典条分法受力分析1基本假定平面应变，滑面成圆弧形。
土力学电子教案之土坡稳定分析
教案表头：教学内容设计及安排第八章土坡稳定分析第一节无粘性土坡的稳定分析【基本内容】天然土坡：由于地质作用而自然形成的土坡。
人工土坡：人们在修建各种工程时，在天然土体中开挖或填筑而成的土坡。
滑坡：土坡丧失其原有稳定性，一部分土体相对另一部分土体滑动的现象。
分析土坡稳定性的目的：验算土坡的断面是否稳定合理，或根据土坡预定高度、土的性 质等已知条件，设计出合理的土坡断面。
简单土坡：土坡的坡顶和底面都是水平面，并伸至无穷远，土坡由均质土组成。
一、一般情况下的无粘性土土坡条件：均质的无粘性土土坡，干燥或完全浸水，土粒间无粘结力分析方法：只要位于坡面上的土单元体能够保持稳定，则整个坡面就是稳定的 滑动力： T =W sin β 垂直于坡面上的分力： N = W cos β最大静摩擦力： T '= N tan ϕ = W cos βtan ϕ 抗滑力与滑动力的比值称为稳定安全系数K ，2K =βϕβϕβtan tan sin tan cos =='W W T T当β=ϕ 时，K =1，土坡处于极限平衡状态。
砂土的内摩擦角也称为自然休止角。
当β＜φ，即K ＞1，土坡就是稳定的。
可取K =1.1~1.5。
【讨论】无粘性土土坡的稳定性与坡高无关，仅取决于坡角β。
二、有渗流作用时的无粘性土土坡分析方法：若渗流为顺坡出流，则渗流方向与坡面平行，此时使土体下滑的剪切力为J W J T +=+βsin 稳定安全系数为JW W JT T F f s +=+=βϕβsin tan cos 对单位土体，土体自重W =γ '，渗透力J =γw i ，水力坡降i =sin β，于是βγϕγβγβγϕβγtan tan sin sin tan cos sat w s F '=+''==【讨论】当坡面有顺坡渗流作用时，无粘性土土坡的稳定安全系数将近乎降低一半。
【例题先自习后讲解】【例8-1】有一均质无粘性土土坡，其饱和重度 γsat =20.0kN/m 3, 内摩擦角ϕ =30°, 若要求该土坡的稳定安全系数为1.20，试问在干坡或完全浸水情况下以及坡面有顺坡渗流时其坡角应为多少度？ 【讨论】有渗流作用的土坡稳定比无渗流作用的土坡稳定，坡角要小得多。
8土坡稳定性分析
土坡稳定分析土坡是具有倾斜坡面的土体，由自然地质作用所形成的土坡，如山坡、江河的岸坡等，称为天然土坡。
由人工开挖或回填而形成的土坡，如基坑、渠道、土坝、路堤等的边坡，则称为人工土坡。
土体自重以及渗透力等在坡体内引起剪应力，如果剪应力大于土的抗剪强度，就要产生剪切破坏，一部分土体相对于另一部分土体滑动的现象，称为滑坡。
滑坡类型第一节无粘性土坡的稳定分析由粗粒土所堆筑的土坡称无粘性土坡一、均质干坡和水下坡均质干坡和水下坡指由一种土组成、完全在水位以上或完全在水位以下，没有渗透水流作用的无粘性土坡。
稳定条件：只要坡面上的土颗粒在重力作用下能够保持稳定，整个土坡就处于稳定状态。
稳定性分析:从坡面上取一土体单元。
土体重量为W。
滑动力T＝W sinα正压力N＝W cosα抗滑力R＝N tan ϕ＝W cosαtanϕϕ—土的内摩擦角；α—土坡的坡角当F s＝1时，α＝ϕ，α称为天然休止角。
土体的稳定安全系数F s 为：αϕαϕαtan tan sin tan cos ====W W T R F s 滑动力抗滑力二、有渗透水流的均质土坡挡水土堤内形成渗流场，如果浸润线在下游坡面逸出，这时在浸润线以下，下游坡内的土体除受重力作用外，还受渗透力的作用，因而会降低下游边坡的稳定性。
在坡面上渗流逸出处取一单元土体v 的土骨架为隔离体，土体除受重力作用外，还受渗透力的作用。
有效重量为W ´＝γ ´V 。
如果水流的方向与水平面成夹角θ，则沿水流方向的渗透力 j ＝γωi 。
作用在土骨架上的总渗透力为 J ＝γωiV 。
沿坡面的全部滑动力（包括重力和渗透力）为 ：坡面的正压力为 )sin(cos )cos(sin θααθαα--'=-+'=J W N J W T ，土体沿坡面滑动的安全系数： )cos(sin tan )]sin(cos [tan θαγαγϕθαγαγϕ--'--'==iV V iV V T N F w w s 若水流在逸出段顺坡面流动， 即θ ＝ α ，i =sin α, 则αγϕγϕtan tan tan sat s T N F '==第二节 粘性土坡的稳定分析粘性土由于粘聚力的存在，粘性土坡不像无粘性土坡一样仅沿坡面表面滑动。
第八章-无粘性土坡稳定分析
渗流作用土坡
• 渗流的影响： 土坡中存在渗流，沿渗流出逸方向产生渗透力； 坡面上土体除受重力外，还受渗透力的作用； 渗透力增大了土体的滑动力，减少了抗滑力。 • 抗滑稳定安全系数： 将重力和渗透力沿平行坡面和垂直坡面分解： 抗滑力：( N1 N2 )tg 滑动力： T1 T2
Fs 则抗滑稳定安全系数为： 抗滑力 ( N1 N2 )tg 滑动力 T1 T2
• 稳定性比较： 1）渗流情况下，无粘性土坡的稳定性比无渗流 情况下差，其安全系数降低约 1/2； 2）无渗流时，=，土坡稳定； 3）有渗流时，坡度就必须变缓才能保持稳定。
土坡稳定性分析
• 计算简图：
无粘性土土坡的稳定性分析
• 分析方法： 直线滑动法 • 全干或全淹没的土坡: 只要坡面上的土粒能够保持稳定，整个土坡稳定。 将坡面上任一土颗粒的重量W分解为平行坡面和 垂直坡面： 下滑力：平行坡面的力 T=Wsin 法向分力：垂直坡面的力 N=Wcos 抗滑力：摩擦力 Tf=Ntg 是坡角； 是土体的内摩擦角 f =tg是摩擦系数
无粘性土土坡的稳定性分析
• 计算简图：
抗滑稳定安全系数
• 土坡的抗滑稳定安全系数： 等于抗滑力Tf与滑动力T之比
Fs Tf T tg tg
• 稳定性评判： Fs1，土坡稳定， Fs=1，土坡处于极限平衡状态，= Fs<1，土坡不稳定，< • 对于均质无粘性土坡，只要坡脚，则无论坡 的高度多大，土坡总是稳定的。
• 计算简图：
土坡稳定性分析
• 计算简图：
滑动面的形状
• 滑动面的形状: 粘性土坡：滑动面的形状呈曲线形； 坡顶处滑动面近于垂直； 接近坡脚处，滑动面与坡脚斜交。 无粘性土坡：滑动面近于直线 分析土坡稳定性时，常按平面问题来计算。 • 复合滑动面： 在土坝坝基中存在软弱夹层时，可能出现由曲线 和直线组成的复合滑动面。 • 土坡稳定性分析的目的：验算土坡的稳定性； 设计出合理的土坡断面。
土坡稳定分析
第八章土坡稳定分析学习指导内容简介土坡的稳定性分析是土力学中重要的稳定分析问题，本章将分别介绍无粘性土坡和粘性土坡的稳定性分析方法，讨论土坡最危险滑裂面的确定方法和土坡稳定分析的图解法，并将简单介绍天然土体上的土坡稳定分析方法。
教学目标重点学习粘性土坡的稳定性分析方法，掌握无粘性土坡和自然土坡的稳定分析方法。
学习要求1、了解无粘性土坡的稳定分析方法2、掌握粘性土坡的稳定分析方法，包括整体圆弧滑动法和条分法（瑞典条分法、毕肖甫法和普遍条分法）；3、掌握粘性土坡最危险滑裂面的确定方法；了解粘性边坡稳定分析的图解法。
4、了解天然土体(裂隙硬粘土和软土地基）上的土坡稳定分析。
基本概念天然土坡、人工土坡、滑坡、圆弧滑动法、条分法、最危险滑动面学习内容第一节概述第二节无粘性土坡稳定分析第三节粘性土坡稳定分析第四节天然土坡的稳定分析第五节复合滑动面的土坡稳定分析第六节土坡稳定分析中的几个问题学时安排本章总学时数：5.5学时第一节 0.5学时第二节 0.5学时第三节 3学时第四节 0.5学时第五节 0.5学时第六节 0.5学时主要内容第一节概述本章主要学习目前常用的土坡稳定分析方法，学习与土的抗剪强度有关的问题。
无粘性土坡稳定分析分两种情况下(全干或全淹没情况、有渗透情况)无粘性土坡稳定分析方法，要求掌握无粘性土坡稳定安全系数的定义及推导过程，坡面有顺坡渗流作用下与全干或全淹没情况相比无粘性土土坡的稳定安全系数有何联系。
粘性土坡的稳定分析：学习其整体圆弧法、瑞典条分法、毕肖甫法、普遍条分法、有限元法等方法在粘性土稳定分析中的应用。
要求掌握圆弧法进行土坡稳定分析及几种特殊条件下土坡稳定分析计算。
边坡稳定分析的总应力法和有效应力法：学习稳定渗流期、施工期、地震期边坡稳定分析方法。
土坡稳定分析讨论三个问题：土坡稳定分析中计算方法问题、强度指标的选用问题和容许安全系数问题。
一、基本概念土坡就是具有倾斜坡面的土体。
由自然地质作用所形成的土坡，如山坡、江河的岸坡等，称为天然土坡(naturalsoilslope)。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
土力学与地基基础
• 由于计算上述安全系数时，滑动面为任意 假定，并不是最危险的滑动面，因此所求 结果并非最小的安全系数。通常在计算时 需要假定一系列滑动面，进行多次试算， 计算工作量很大。 • W.费伦纽斯（Fellenius,1927）通过大量计 算分析，提出了以下所介绍的确定最危险 滑动面圆心的经验方法。
土力学与地基基础
瑞典条分法和毕肖普法的比较
• 瑞典条分法忽略各条间力对Ni的影响，i土 条上只有Gi,Ni,Ti三种力作用，低估安全系 数5~20%。 • 毕肖普法忽略土条竖向剪切力的作用，考 虑了土条两侧的作用力，比瑞典条分法更 合理，低估安全系数约为2~7%。
土力学与地基基础
li
K
1 m cb Gi ui b X i tan i
G sin
i
i
土力学与地基基础
• 毕肖普条分法考虑了土条两侧的作用力， 计算结果比较合理。 • 分析时先后利用每一土条竖向力的平衡及 整个滑动土体的力矩平衡条件，避开了Ei 及其作用点的位置，并假定所有的 X i 均等 于零，使分析过程得到了简化。 • 但该方法同样不能满足所有的平衡条件， 还不是一个严格的方法，由此产生的误差 约为2%～7%。另外，毕肖普条分法也可以 用于总应力分析，即在上述公式中采用总 应力强度指标c、φ计算即可。
土力学与地基基础
土坡形态及各部分名称
坡肩 坡顶
坡高 坡脚
坡面
坡角
土力学与地基基础
土力学与地基基础
土力学与地基基础
土力学与地基基础
4.土坡由于其表面倾斜，在自重或外部荷 载的作用下，存在着向下移动的趋势， 一旦潜在滑动面上的剪应力超过了该面 上的抗剪强度，稳定平衡遭到破坏, 就可 能造成土坡中一部分土体相对于另一部 分的向下滑动，该滑动现象称为滑坡。 5.天然的斜坡、填筑的堤坝以及基坑放坡 开挖等问题，都要演算土坡的稳定性。 亦即比较可能滑动面上的剪应力与抗剪 强度，这种工作称为稳定性分析。
φ
C
φ 15 φ2 ° 0 φ2 ° 5 φ3 ° 0°
φ1 0°
5°
1:1 1:1.5 1:2 1:2.5 1:3
土力学与地基基础
土力学与地基基础
二、瑞典条分法(Fellenius method)
• 瑞典条分法是将滑动土体竖直分成若干个 土条，把土条看成刚体，分别求出作用于 各个土条上的力对圆心的滑动力矩和抗滑 力矩，然后按式8-4求土坡的稳定安全系数。 • 由于该方法是瑞典人费伦纽斯（W.Fellenius） 等首先提出来的，所以称为瑞典条分法， 又称为费伦纽斯条分法。
土力学与地基基础
第八章 土坡稳定性分析
• 本章提要与学习目标 • 土坡在自重或外部荷载作用下，存在着 向下移动的趋势。分析土坡的稳定性， 即比较可能滑动面上的剪应力与抗剪强 度，是土力学中的重要问题之一。 • 本章主要内容有无粘性土坡的稳定性分 析和粘性土坡的稳定性分析。后者是本 章的重点内容，包括整体圆弧滑动法、 瑞典条分法、毕肖普条分法和简布条分 法等。
li
b Xi+1 Ei+1 hi+1
土力学与地基基础
• 滑动面上的抗滑力产生的抗滑力矩为
T R
i
ci li N i tan i R
K
Gi cos i tan i
i i
• 安全系数的计算公式为
c l K
i i
G sin
土力学与地基基础
•从瑞典条分法的分析过程可以看出，该法 忽略了土条之间力的相互影响，只满足于滑 动土体整体的力矩平衡条件，却不满足土条 块之间的静力平衡条件，是一种简化的计算 方法。这是它区别于后面将要介绍的其它条 分法的主要特点。 •由于该方法应用的时间很长，积累了丰富 的工程经验，一般得到的安全系数偏低，即 误差偏于安全，所以目前仍然是工程上常用 的方法。
土力学与地基基础
土力学与地基基础
坡比是坡的垂直高度与水平宽度的比值。即坡角的正切值。
设坡角为α，坡度为i，则i=h:l 坡度一般写成1∶m的形式。 坡度越大，则坡角越大，坡面就越陡
土力学与地基基础
土力学与地基基础
• 土坡的稳定分析大都需要经过试算，计算 工作量非常大，因此，不少学者提出简化 的图表计算法。 • 8-6给出根据计算资料整理得到的极限状态 时均质土坡内摩擦角，坡角β与稳定数 Ns( stability number)（数值范围0～0.25）之 间的关系曲线，其中
土力学与地基基础
• 掌握土坡稳定性分析方法是土力学的基本 学习目标之一，是工程实际当中判断天然 土坡和由岩土填筑与开挖形成的人工土坡 安全性的重要技能。 • 通过本章的学习，应掌握无粘性土坡的稳 定性分析方法以及诸如整体圆弧滑动法、 瑞典条分法、毕肖普条分法和简布条分法 等针对粘性土坡的稳定性分析方法。
土力学与地基基础
剪应力达到抗剪强度的原因： ① 剪应力增大：土坡上施加过量荷载，降雨 使土体饱和等； ② 抗剪强度减小：孔隙水压力增大，气候变 化产生开裂、冻融等。
土力学与地基基础
第二节 无粘性土土坡稳定分析
1.无粘性土坡(slope of non-cohesion soil)即是由粗 颗粒土所堆筑的土坡。 2.原理：当抗滑力<滑动力时，土坡稳定； 当抗滑力>滑动力时，土坡失稳； 3.土体的稳定安全系数k 抗滑力 R tan k 滑动力 T tan M M
土力学与地基基础
土力学与地基基础
土力学与地基基础
计算步骤
1. 2. 3. 4. 5. 6. 7. 8. 按比例尺，画坡。 确定圆心O和半径R，画弧。 分条，bi=R/10，编号 计算每个土条的自重 分解Gi滑动面的两个分力Ni,Ti 计算滑动力矩 计算抗滑力矩 求稳定系数K
土力学与地基基础
三、毕肖普条分法(Bishop method)
f K
土力学与地基基础
• 若以滑动面上的最大抗滑 力矩与滑动力矩之比来定 义，其结果完全一致。如 图8-4所示土坡，AC为假 定的滑动面，圆心为O， 半径为R，当土体ABC稳 定时必须满足力矩平衡条 件，（滑动面上的法向反 力过圆心），故稳定安全 系数为
a O A
B R
G C N
抗滑力矩 f ACR K 滑动力矩 Ga
tan tan Fs w） sat tan T （ tan
Tf
tan 1 tan Fs T sat tan 2 tan
Tf
与干土相比降低1/2
土力学与地基基础
0
J
T
W
[ cos i w sin( )] tan Fs T sin i w cos( ) Tf
• A.W.毕肖普（Bishop,1955）假定各土条底 部滑动面上的抗滑安全系数均相同，即等 于整个滑动面的平均安全系数。 • 取单位长度土坡按平面应变问题计算，如 图8-9所示。设可能滑动面为一圆弧AC，圆 心为O，半径为R。
土力学与地基基础
O xi R A Ei Xi Gi C c T i bi b B a Gi d Ni' uili Xi+1 Ei+1 hi
土力学与地基基础
第一节 概述
1.具有倾斜表面的土体称为土坡 。 2.土坡根据其成因可分为两种：一种是由 于地质作用而自然形成的，称为天然土 坡，如山坡、江河的岸边；另一种是人 们在修建各种工程时，在天然土体中开 挖或填筑而形成的，称为人工土坡。 3.当均质土的土坡坡顶与坡底平行，坡面 为同一坡度时，称为简单土坡。
影 响 土 坡 稳 定 性 的 主 要 因 素
土坡高度
土的性质
气象条件
地下水的渗透
地震
人为因素
土力学与地基基础
6.土坡失稳的类型比较复杂，大多是土体的塑 性破坏。 7.土体塑性破坏的分析方法有极限平衡法(limit equilibrium method)、极限分析法(limit analysis method)和有限元法(finite element method)等。 8.一般土坡的长度远超过其宽度，故对土坡进 行稳定性分析时，常沿长度方向取单位长度按 平面问题计算。
J
T
W
[ cos i w sin( )] tan Fs T sin i w cos( ) Tf
N
分析：1.当渗流顺坡时 =
i sin
[ cos i w sin(0)] tan Fs T sin sin w cos(0) Tf
J
T
W
N
J i w
J产生的下滑力和法向 力分别为
.
i w cos( ) i w sin( )
[ cos i w sin( )] tan Fs T sin i w cos( ) Tf
土力学与地基基础
c NS h
土力学与地基基础
稳定数计算图
0.24 0.22 R 0.20 0.18 0.16 0.14 0.12 0.10 0.08 0.06 0.04 0.02 0 90 85 80 75 70 65 60 55 50 45 40 35 30 25 20 15
β (°)
O B
β
A h
Ns---c/γ h
土力学与地基基础 把滑动土体分成若干个土条后，土条的两个侧面分别 存在着条块间的作用力（图8-7）。任取一条块i作为 研究对象。
• 重力Gi 产生的滑动力矩为
G x G R sin
i i i
O xi R
i
• 式中，Xi为条块i对O点的力臂长度。
bi B A a Ei Gi C hi Xi c T i Gi d Ni