现代控制理论 第5章线性时不变系统的多项式矩阵描述
绪论

出生日期: 1831年06月13日 逝世日期: 1879年11月5日 职业: 物理学家
Harbin Engineering University
3 公因子和最大公因子
公因子的定义
• 相同列数的两个多项式矩阵间可以定义右公因子(是多项式 矩阵).假定N(s)和D(s)列数相同,若 N ( s) N ( s) R( s)
D(s) D (s) R(s) 则R(s)称为N(s)和D(s)的右公因子.
认识他们吗??
Edward John Routh :1831年1月20日出 生在加拿大的魁北克。
Routh 11岁那年回到英国,在de Morgan指导下学 习数学。在剑桥学习的毕业考试中,他获得第一名。并 得到了“Senior Wrangler”的荣誉称号。 毕业后Routh开始从事私人数学教师的工作。从 1855年到1888年Routh教了600多名学生,其中有27位获 得“SEnior Wrangler”称号。建立了无可匹敌的业绩。
Harbin Engineering University
哈罗德·史蒂芬·布莱克( Harold Stephen Black)
Harold Stephen Black (April 14, 1898 – December 11, 1983) was an American electrical engineer, who revolutionized the field of applied electronics by inventing the negative feedback amplifier in 1927. To some, his invention is considered the most important breakthrough of the twentieth century in the field of electronics, since it has a wide area of application. However, a negative feedback amplifier can be unstable such that it may oscillate. Once the stability problem is solved, the negative feedback amplifier is extremely useful in the field of electronics. Black published a famous paper, Stabilized feedback amplifiers, in 1934.
现代控制理论知识点汇总

现代控制理论知识点汇总Revised at 2 pm on December 25, 2020.第一章 控制系统的状态空间表达式1. 状态空间表达式 n 阶DuCx y Bu Ax x+=+= 1:⨯r u 1:⨯m y n n A ⨯: r n B ⨯: n m C ⨯:r m D ⨯:A 称为系统矩阵,描述系统内部状态之间的联系;B为输入(或控制)矩阵,表示输入对每个状态变量的作用情况;C 输出矩阵,表示输出与每个状态变量间的组成关系,D直接传递矩阵,表示输入对输出的直接传递关系。
2. 状态空间描述的特点①考虑了“输入-状态-输出”这一过程,它揭示了问题的本质,即输入引起了状态的变化,而状态决定了输出。
②状态方程和输出方程都是运动方程。
③状态变量个数等于系统包含的独立贮能元件的个数,n 阶系统有n 个状态变量可以选择。
④状态变量的选择不唯一。
⑤从便于控制系统的构成来说,把状态变量选为可测量或可观察的量更为合适。
⑥建立状态空间描述的步骤:a 选择状态变量;b 列写微分方程并化为状态变量的一阶微分方程组;c 将一阶微分方程组化为向量矩阵形式,即为状态空间描述。
⑦状态空间分析法是时域内的一种矩阵运算方法,特别适合于用计算机计算。
3. 模拟结构图(积分器 加法器 比例器)已知状态空间描述,绘制模拟结构图的步骤:积分器的数目应等于状态变量数,将他们画在适当的位置,每个积分器的输出表示相应的某个状态变量,然后根据状态空间表达式画出相应的加法器和比例器,最后用箭头将这些元件连接起来。
4. 状态空间表达式的建立① 由系统框图建立状态空间表达式:a 将各个环节(放大、积分、惯性等)变成相应的模拟结构图;b 每个积分器的输出选作i x ,输入则为i x;c 由模拟图写出状态方程和输出方程。
② 由系统的机理出发建立状态空间表达式:如电路系统。
通常选电容上的电压和电感上的电流作为状态变量。
利用KVL 和KCL 列微分方程,整理。
现代控制理论-09(第5章状态反馈控制器设计)

期望的闭环特征多项式
(λ − λ1 )(λ − λ 2 )(λ − λ3 ) = λ3 + b2 λ2 + b1 λ + b0
要实现极点配置,须
λ3 + (a 2 + k 2 )λ2 + (a1 + k1 )λ + a 0 + k 0 = λ3 + b2 λ2 + b1λ + b0
a 0 + k 0 = b0 a1 + k1 = b1 a 2 + k 2 = b2
− 设计一个状态反馈控制器,使得闭环极点是-2, 1 ± j
解
确定能控标准型实现
1 0⎤ ⎡0 ⎡0 ⎤ x = ⎢0 0 1⎥ x + ⎢0⎥u ⎢ ⎥ ⎢ ⎥ ⎢0 − 2 − 3⎥ ⎢1⎥ ⎣ ⎦ ⎣ ⎦ y = [10 0 0]x
状态反馈控制器 u = − Kx ,K = [k1 k 2 k3 ] 闭环多项式:det[λI − ( A − BK )] = λ3 + (3 + k 3 )λ2 + (2 + k 2 )λ + k1 期望多项式: (λ + 2)(λ + 1 − j)(λ + 1 + j) = λ3 + 4λ2 + 6λ + 4
问题:对一般状态空间模型,如何解极点配置问题? 思路:考虑能控状态空间模型 将能控状态空间模型等价地转化为能控标准型 如何从能控标准型模型的解导出一般模型的极 点配置控制器。
系统模型
x = Ax + Bu
~ TAT −1 = A, ~ TB = B
0 ⎤ 0 ⎥ ⎥ ⎥, ⎥ 1 ⎥ − an−1 ⎥ ⎦ ⎡0 ⎤ ⎢0 ⎥ ~ ⎢ ⎥ B=⎢ ⎥ ⎢ ⎥ ⎢0 ⎥ ⎢1⎥ ⎣ ⎦
现代控制理论习题解答(第五章)

第五章 状态反馈和状态观测器3-5-1 已知系统结构图如图题3-5-1图所示。
(1)写出系统状态空间表达式;(2)试设计一个状态反馈矩阵,将闭环极点特征值配置在j 53±-上。
)(t y题3-5-1图【解】:方法一:根据系统结构直接设状态变量如题3-5-1图所示,写状态空间表达式:[]x y u x x 10112101=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--= 23111=⎥⎦⎤⎢⎣⎡--=c c U rank U系统能控,可以设计状态反馈阵。
设状态反馈阵为][21k k K = 状态反馈控制规律为:Kx r u -= 求希望特征多项式:34625)3()(*22++=++=s s s s f求加入反馈后的系统特征多项式:)22()3()(1212k s k k s bK A sI s f ++-++=+-=依据极点配置的定义求反馈矩阵:]1316[131634)22(6)3(21112=⎩⎨⎧==⇒⎩⎨⎧=+=+-K k k k k k 方法二:[][][]1316)346(311110)(*10211=++⎥⎦⎤⎢⎣⎡--==--I A A A f U K c方法三:(若不考虑原受控对象的结构,仅从配置极点位置的角度出发)求系统传递函数写出能控标准型:2321)111()()(2++-=+-+=s s ss s s U s Y []xy u x x 10103210-=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--= 求系统希望特征多项式:34625)3()(*22++=++=s s s s f求状态反馈矩阵K ~:[][][]33236234~21=--==k k K [][][][]5.05.031111010111=⎥⎦⎤⎢⎣⎡--==--Ab bP⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=105.05.011A P P P []1316~==P K K依据系统传递函数写出能控标准型ss s s s s s U s Y 2310)2)(1(10)()(23++=++= []x y u x x 0010100320100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=求系统希望特征多项式:464]1)1)[(2()(*232+++=+++=s s s s s s f求状态反馈矩阵:[][][]144342604321=---==k k k K 。
现代控制理论第版课后习题答案

现代控制理论第版课后习题答案Prepared on 22 November 2020《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下: 系统的状态方程如下: 令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:1-4 两输入1u ,2u ,两输出1y ,2y 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示: 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令..3.21y x y x y x ===,,,则有相应的模拟结构图如下: 1-6 (2)已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++= 1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘(1) 画出其模拟结构图 (2) 求系统的传递函数 解:(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量(3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解:A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得:3,2,1321-=-=-=λλλ当11-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得: 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P(或令111-=p ,得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ) 当21-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得: 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1423222122p p p P(或令112=p ,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P )当31-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得: 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P1-9将下列状态空间表达式化成约旦标准型(并联分解)(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解:A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解:(1)串联联结 (2)并联联结1-11 (第3版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-11(第2版教材) 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数 解:1-12 已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u 的系数b(即控制列阵)为(1)⎥⎦⎤⎢⎣⎡=11b解法1: 解法2:求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以,状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
现代控制理论基础_周军_第五章状态反馈与状态观测器
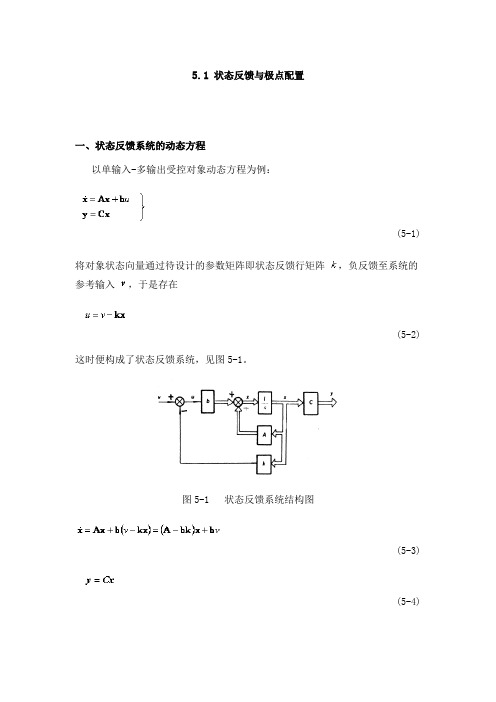
5.1状态反馈与极点配置一、状态反馈系统的动态方程以单输入-多输出受控对象动态方程为例:(5-1)将对象状态向量通过待设计的参数矩阵即状态反馈行矩阵,负反馈至系统的参考输入,于是存在(5-2)这时便构成了状态反馈系统,见图5-1。
图5-1 状态反馈系统结构图(5-3)(5-4)式中v为纯量,为维向量,为维矩阵,为维向量,为维行矩阵,为维向量,为维矩阵。
为闭环状态阵,为闭环特征多项式。
二、用状态反馈使闭环极点配置在任意位置上的充要条件是:受控对象能控证明若式(5-1)所示对象可控,定可通过变换化为能控标准形,有若在变换后的状态空间内引维状态反馈矩阵:(5-5)其中分别为由状态变量引出的反馈系数,则变换后的状态反馈系统动态方程为:(5-6)(5-7)式中(5-8)该式与仍为能控标准形,故引入状态反馈后,系统能控性不变。
特征方程为:(5-9)显见,任意选择阵的个元素,可使特征方程的个系数满足规定要求,能保证特征值(即闭环极点)任意配置。
将逆变换代入式(5-6),可求出原状态空间内的状态反馈系统状态方程:(5-10)与式(5-3)相比,式(5-10)所示对象应引入状态反馈阵为:(5-11)需指出,当受控对象可控时,若不具有能控标准形形式,并不必象如上证明那样去化为能控标准形,只要直接计算状态反馈系统闭环特征多项式,这时,其系数为的函数,与给定极点的特征多项式系数相比较,便可确定。
能控的多输入-多输出系统,经如上类似分析可知,实现闭环极点任意配置的状态反馈阵K为维。
若受控对象不稳定,只要有能控性,完全可由状态反馈配置极点使系统稳定。
状态变量受控情况下,引入状态反馈表示增加一条反馈通路,它能改变反馈所包围环节的传递特性,即通过改变局部回路的极点来改变闭环极点配置。
不能控状态变量与控制量无关,即使引入状态反馈,对闭环极点位置也不会产生任何影响,这是因为传递函数只与系统能控、能观测部分有关的缘故。
若不能控状态变量是稳定的状态变量,那么系统还是能稳定的,否则,系统不稳定。
《现代控制理论基础》第2版 现代控制理论基础_上海交通大学_施颂椒等_PPT_第5章

① 定义 有理函数 g(s) 当s 时,
② g(假)设
常n数(s〔) d(s) g(s)〕, 就称为正那么有理函数。
③ g假( 设)那么有理函数。
④
假g(设) 〔 n(s)d(s)
g(〕s) , 就是 非正那么有理函数。
有理函数阵 G (s) 假设G() 0 ,那G (s么) 是严格正那么有理函数阵〔其每个元均为
G (s) C (sI A )1BD
那么(称A,B,C,D) 是G (s) 的一个实现。
•实现研究的问题
⑴ G (s)可实现为 (A,B,C,D) 的条件问题 ⑵ G (s) 实现的方法
〔5-1〕
•最小实现
如果 (A,B,C,D)是G (s) 的一个实现,那么其所有等价系统也都是其 实现 。 G (s) 可有不同维数的实现,其中维数最小的实现称为最小实 现。它描述了系统的既能控又能观的局部。通常要求的实现 为最小实现。
s 1 s4 s(s1) (s1)s(3) (s1)s(3)
s
1
3
s(s 1 )s( 2 ) (s 1 )s( 2 )s( 3 ) s(s 1 )s( 2 )s( 3 )
G (s) 的特征多项式为:s(s1)s(2)s(3),deG g(s)4。
⑵ G (s) 可实现为 (A,B,C,D) 的条件
③ 非正那么传递函数〔G() 〕,也存在实现,其实现具有
④ 如下形式
Ex(t)A(xt)Bu(t) y(t)Cx(t)Du(t)
〔5-9〕
式中 E为奇异阵。这种形式的系统称为广义系统,或奇异 系统。(本书不予讨论,在专门文献中研究)
5.2.2 最小实现的性质
如果将例〔5-5〕的传递函数阵写成
G ( s ) G 1 ( s )G 2 ( s )
《现代控制理论》第3版课后习题答案
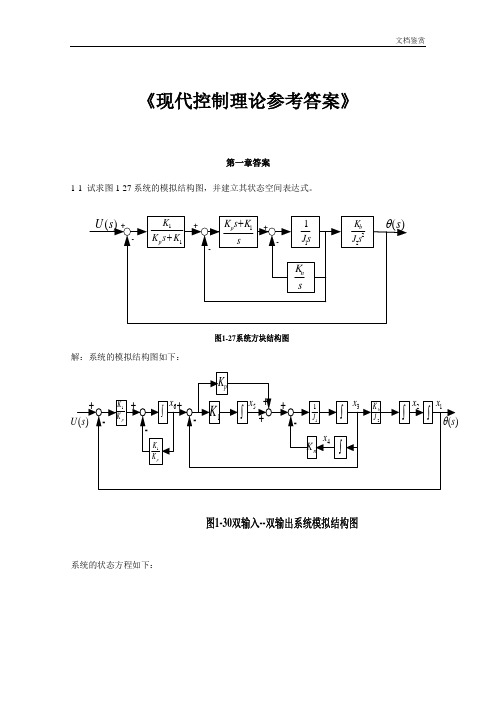
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc ---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2解020/耦6/17零点。
15
1. 输入解耦零点(input decoupling zero)
若{P(s),Q(s),R(s),W(s)}中,P(s)、Q(s)存在非单模的 gcld H(s),即
P(s) H (s)P (s), Q(s) H (s)Q (s), 则
G(s) R(s)[H (s)P (s)]1[H (s)Q (s)] W (s)
Cˆ(s)
E(s)uˆ(s)
2020/6/17
4
3.矩阵分式描述的PMD
给定G(s) N (s)D1(s)+E(s)
则等价的PMD为: D(s)ˆ
(s)
E(s)uˆ(s)
三.不可简约PMD
不可简约PMD:{P(s),Q(s)}左互质,且{P(s),R(s)}
2020/6/17
strictly proper
10
-对 Pr1(s)Q求r (s观) 测器形实现(利用上节方法), 得 {Ao, Bo ,C必o}有,
Co (sI Ao )1 Bo Pr1(s)Qr (s) ( Ao ,Co )observable
(s) [Pr1(s)Qr (s) Y (s)]u(s)
则:{D(s),N(s)}右互质{A,C}能观 (已经能控)
对左MFD,DL1(s)NL (s) DL1(s)NL (s) EL (s)
能观类实现: {A, B,C , E},dim A deg det DL (s),则
2020/6/17
{DL (s), NL (s)}右互质 {A, B}能控
同一系统,其PMD为{P(s),Q(s),R(s),W(s)},
系统极点是det P(s)=0的根
状态空间描述为{A,B,C,E}
系统极点是det(sI-A)=0的根
以上二者是等同的。
系统极点并不全是传递函数矩阵的极点,因求传递函数 矩阵时可能发生零极对消。
对消掉的零极点不包含在传递函数矩阵中,成为系统的
R(s)P (s)1Q (s) W (s)
可见,H(s)在传递函数矩阵中消失了,这导致了零极点对消。
定义:det H(s)=0的根为输入解耦零点。
意义:这种对消的零极点使系统的输入与分状态之间解除了
耦合,即输入信号不能影响这些极点所对应的状态。
由于
[P(s) Q(s)] H (s)[ P (s) Q (s)] rank[P (s) Q (s)] m,s C
即
P(s) L(s)P1(s) Q(s) L(s)Q1(s)
P(s) P2 (s)L(s) 则
R(s) R1(s)L(s)
G(s) R(s)P11(s)Q1(s) W (s) R1(s)P21(s)Q(s) W (s)
显然,L(s)的零点都是解耦点,并且既是i.d.z., 又 是o.d.z.这样的L(s) 的零点称为输入输出解耦零点, i.o.d.z
P(s)F (s) (s) Q(s)u(s)
y(s) R(s)F (s) (s) W (s)u(s) 设%(s) F (s) (s),则
P(s)%(s) Q(s)u(s)
y(s)
R
(s)%(s)
W
(s)u(s)
不可简约
rank P(s) Q(s) rank P(s) Q(s) ,故P(s),Q(s)左互质.
20
➢ MFD的系统矩阵:
线性定常系统右MFDN (s)D1(s的) 系统矩阵定义为:
S(s)=
D(s) -N(s)
Ip
0
左MFDDL1(s)NL (的s) 系统矩阵为:
S(s)=
DL (s) -Iq
NL (s)
0
2020/6/17
21
2 判断PMD的不可简约性
• 互质性与能控性、能观性的等价性
1.给定{P(s),Q(s),R(s),W(s)},其维数为n=deg detP(s)=dimA
的一个实现为{A,B,C,E(p)},则
{P(s),Q(s)}左互质{A,B}能控
{P(s),R(s)}右互质{A,C}能观
2. 对右MFD,N (s)D1(s) N (s)D1(s) E(s) 能控类实现:{A,B,C,E},dimA=deg detD(s)
第5章 线性时不变系统的 多项式矩阵描述
5.1 多项式矩阵描述(PMD) 5.2 多项式矩阵描述的状态空间实现 5.3 多项式矩阵描述的互质性和状态空间描
述的能控性与能观测性 5.4 传输零点和解耦零点 5.5 系统矩阵和严格系统等价
主要的数学描述
输入 输出 描述
状态 空间 描述
矩阵 分式 描述
系统 矩阵 描述
的实现。 • 步骤:
– 先把 P1(s)Q化(s)成满足左MFD求实现的条件,即 P(s)化为行既约, Pr1(s)严Qr (格s) 真;
(s) P1(s)Q(s)u(s) [1M4(s2)P4(s3)]1[1M4(s2)Q4(s3)]u(s)
Pr (s)
Qr (s)
Pr1(s)Qr (s)u(s) [Y (s) 1Pr41(s2)Q4r (3s)]u(s)
• 注:PMD实现具有强不唯一性
二 .构造PMD实现的方法
以构造观测器形实现为最简便 已知:{P(s),Q(s),R(s),W(s)}, 求实现
2020/6/17
9
• 思路: – 前面已讲过的MFD实现方法,要求分母矩阵行 (列)既约,严格真;
– 在P(s)ζ(s)=Q(s)u(s)中,先求 (s) P1(s)Q(s)u(s)
2020/6/17
18
• 注:
– 求传递函数矩阵时,应消去P(s)与Q(s)的左 公因子和P(s)和R(s)的右公因子,使传递函 数矩阵的零极点不包含解耦零点。
– 若记P和Z为传递矩阵的极点、零点,则系 统的极点Ps和零点Zs分别为
Ps P i.d.z o.d.z i.o.d.z Zs Z i.d.z o.d.z i.o.d.z
13
3.对{A,B,C,E(p)}, G(s) C(sI A)1 B E(s) {A,B}能控{sI-A,B}左互质 {A,C}能观{sI-A,C}右互质 此即为PBH秩判据的结论。
4.SISO系统{A,b,c},
g(s) c(sI A)1b c adj(sI A) b N (s) det(sI A) (s)
2020/6/17
8
5.2 PMD的状态空间实现
一. PMD实现的定义
给定{P(s),Q(s),R(s),W(s)},若能找到状态空 间描述{A,B,C,E(p)},使
R(s)P1(s)Q(s) W (s) C(sI A)1 B E(s) 则称{A, B,C, E( p)}为给定PMD的实现.
同前, 输出解耦零点又等同于使 RP((ss))降秩的所有s值.
意义:输出解耦零点使输出与分状态之间的耦合解除了,即分
202状0/6态/17 不完全反映到系统输出中去。
17
3. 输入输出解耦零点
若P(s)和Q(s)存在非单模的左公因子L(s), (不一定gcld)
同时P(s)和R(s)也存在非单模的右公因子L(s)
此时,P(s),Q(s)有非单模的gcld, 设为H(s),非奇异
则
P(s) H (s)P(s)
Q(s) H (s)Q(s)
P (s), Q(s)左互质
P(s) (s) Q(s)u(s)两边左乘H 1(s), 得
P(s) (s) Q(s)u(s)
y(s)
R(s)
(s)
W
(s)u(s)
不可简约
rank
P(s) R( s)
rank
P(s)
R(s)
,
故P(s),
R(s)右互质.
2020/6/17
6
(2) P(s),Q(s)左互质,P(s),R(s)非右互质
P(s),R(s)有非单模的gcrd, 设为F(s), 必非奇异
P(s) P(s)F (s) R(s) R(s)F (s) P(s), R(s)右互质 原描述可写成
C(sI Ao )1 Bou(s) E(s)u(s)
实现为 2020/6/17 {A, B,C, E( p)}
11
[结论]
对线性时不变系统的PMD(P(s),Q(s),R(s),W(s)),
表 P1(s)Q(s) Pr1(s)Qr (s) Pr1(s)Qr (s) Y (s)
而 {Ao, B为o,C严o}真
-总之
Co (sI Ao )1 Bou(s) Y (s)u(s)
y(s) R(s) (s) W (s)u(s)
1R(2s)C3 o (sI Ao )1 Bou(s) [R(s)Y (s) W (s)]u(s)
X (s)(sI Ao )C
C(sI Ao )1 Bou(s) [ X (s)Bo R(s)Y (s) W (s)]u(s)
2020/6/17
2
5.1 多项式矩阵描述(PMD)
一 多项式矩阵描述的形式
多输入多输出线性定常系统:
输入u=
uM1
,广义状态
=
1
M,输出y=
yM1
up
m
yq
系统的多项式矩阵描述为:
)
P(s)
(s)
Q(s)u) (s)
y) (s)
)
R(s)
(s)
W
(s)u) (s)
注:它是系统的内部描述,是最一般的描述。
右互质
不可简约PMD不唯一
{P(s),Q(s),R(s),W(s)}不可简约
{U(s)P(s)V(s),U(s)Q(s),R(s)V(s),W(s)}不可简约
U(s),V(s)为单模矩阵
