201力在平面坐标上的投影
合集下载
理论力学-力的分解与力的投影以及平面力系中的力矩
F Fx2 Fy2
cos Fx
F
cos Fy
F
式中的α和β分别表示力F与x轴和y轴正向间的夹角。
第一章 静力学的基本公理与受力分析
合力投影定理
合力在任一轴上的投影等于各分力在同一轴上投影的代数和。
F R F 1 F 2 L L F nF
F R F x i F y j,F i F x ii F y ij( i 1 ,2 ,L n )
第一章 静力学的基本公理与受力分析
例题
平面基本力系
合力的大小:
FR Fx2Fy217.31N
合力与轴x,y夹角的方向余弦为:
cos Fx 0 .754
FR
cos F y 0 .656
FR
所以,合力与轴x,y的夹角分别为:
40.99
49.01
第一章 静力学的基本公理与受力分析
F2 y
三、力在空间坐标轴上的投影
力在空间正交坐标轴上的投影可用两种方法来计算
直接投影法
z
Fx F cos
F
y
F
cos
F z F c o s
F
F = Fx+Fy+Fz= Fx i+Fy j+Fz k
O
y
x
第一章 静力学的基本公理与受力分析
二次投影法
z
F = Fx+Fy+Fz= Fx i+Fy j+Fz k
力F使物体绕O点转动效果的量度取决于三个因素: (1)力F的大小与力臂的乘积,即力矩的大小; (2)力F与矩心O所确定的平面的方位,即力矩的作用面; (3)在作用面内,力F绕矩心O的转向。
第一章 静力学的基本公理与受力分析
cos Fx
F
cos Fy
F
式中的α和β分别表示力F与x轴和y轴正向间的夹角。
第一章 静力学的基本公理与受力分析
合力投影定理
合力在任一轴上的投影等于各分力在同一轴上投影的代数和。
F R F 1 F 2 L L F nF
F R F x i F y j,F i F x ii F y ij( i 1 ,2 ,L n )
第一章 静力学的基本公理与受力分析
例题
平面基本力系
合力的大小:
FR Fx2Fy217.31N
合力与轴x,y夹角的方向余弦为:
cos Fx 0 .754
FR
cos F y 0 .656
FR
所以,合力与轴x,y的夹角分别为:
40.99
49.01
第一章 静力学的基本公理与受力分析
F2 y
三、力在空间坐标轴上的投影
力在空间正交坐标轴上的投影可用两种方法来计算
直接投影法
z
Fx F cos
F
y
F
cos
F z F c o s
F
F = Fx+Fy+Fz= Fx i+Fy j+Fz k
O
y
x
第一章 静力学的基本公理与受力分析
二次投影法
z
F = Fx+Fy+Fz= Fx i+Fy j+Fz k
力F使物体绕O点转动效果的量度取决于三个因素: (1)力F的大小与力臂的乘积,即力矩的大小; (2)力F与矩心O所确定的平面的方位,即力矩的作用面; (3)在作用面内,力F绕矩心O的转向。
第一章 静力学的基本公理与受力分析
学习任务4:投影、力矩、力偶

?
l
3 o
θ
2
C
1
G
解: MO(F) = Fd
位置1: MO(F) = Gd = 0 位置2: MO(F) = -G -Glsinθ
Gd=lsinθ 位置3: MO(F) = -Gl
陕西铁路工程职业技术学院结构教研室
LOGO
三、力偶及力偶矩
由大小相等、方向相反、不共线的两个力组d成 F′
的力系称为力偶。(F,F’) 力偶对物体的效应:只产生转动效应,而无F移动效应。
M=±F.d
陕西铁路工程职业技术学院结构教研室
d F′
d F′
F
F
❖ ⑴力偶没有合力。一个力偶不能用一个力代替,也不能与一个 力平衡。力偶在任一轴上的投影为零。
平面汇交力系的合力在某轴上的投影等于力系 中各分力在同一轴上投影的代数和。即:
Rx = X1 + X2 + ···Xn= ∑ X Ry = Y1 + Y2 + ···Yn = ∑ Y
R = √ (∑X )2 + (∑ Y ) 2
∑Y Tanα= ∑ X
陕西铁路工程职业技术学院结构教研室
合力投影定理应用
1.6 力矩和力偶
陕西铁路工程职业技术学院结构教研室
一、力矩
❖ 定义:力与力臂的乘积冠以正、负号定义为力F对O点的力 矩。
表达式:Mo(F) = ±F·d
F1 F2
O — 转动的中心。称为力矩中
O
心,简称矩心
d — 转动中心到力作用线之 间的距离称为力臂(注意单位)
正负号规定:若力使物体绕矩心作逆时针 转向转动力矩取正号,反之取负号。
1.5 力的投影
一、力在平面直角坐标轴上的投影
l
3 o
θ
2
C
1
G
解: MO(F) = Fd
位置1: MO(F) = Gd = 0 位置2: MO(F) = -G -Glsinθ
Gd=lsinθ 位置3: MO(F) = -Gl
陕西铁路工程职业技术学院结构教研室
LOGO
三、力偶及力偶矩
由大小相等、方向相反、不共线的两个力组d成 F′
的力系称为力偶。(F,F’) 力偶对物体的效应:只产生转动效应,而无F移动效应。
M=±F.d
陕西铁路工程职业技术学院结构教研室
d F′
d F′
F
F
❖ ⑴力偶没有合力。一个力偶不能用一个力代替,也不能与一个 力平衡。力偶在任一轴上的投影为零。
平面汇交力系的合力在某轴上的投影等于力系 中各分力在同一轴上投影的代数和。即:
Rx = X1 + X2 + ···Xn= ∑ X Ry = Y1 + Y2 + ···Yn = ∑ Y
R = √ (∑X )2 + (∑ Y ) 2
∑Y Tanα= ∑ X
陕西铁路工程职业技术学院结构教研室
合力投影定理应用
1.6 力矩和力偶
陕西铁路工程职业技术学院结构教研室
一、力矩
❖ 定义:力与力臂的乘积冠以正、负号定义为力F对O点的力 矩。
表达式:Mo(F) = ±F·d
F1 F2
O — 转动的中心。称为力矩中
O
心,简称矩心
d — 转动中心到力作用线之 间的距离称为力臂(注意单位)
正负号规定:若力使物体绕矩心作逆时针 转向转动力矩取正号,反之取负号。
1.5 力的投影
一、力在平面直角坐标轴上的投影
空间力系沿坐标的分解与投影

6-1
空间力系沿坐标的分解与投影
空间力系 空间力的 分解 二次投影法 应用举例
A
空间力系
各力的作用线不在同一平面内 可分成
空间汇交力系 空间力偶系 空间任意力系(最一般的系)
与平面一般力系的不同
研究方法基本相同 概念、理论和方法要推广和引伸
B
空间力的分解
空间的力F
z
• 把其向各坐标轴分解 Z Fx,Fy,Fz •投影为 X=F cosα Y=F cosβ Z=F cosγ
x O
Fz Fx
C
E
γ
F
A
B
α
β
Fy
Dቤተ መጻሕፍቲ ባይዱ
y Y X
C
二次投影法
把力向z轴上投影 • 把力向oxy平面投影 • 把oxy平面上的投影
– 向x轴投影 – 向y轴投影
O z Z A C X E B
F
θ
Y
D
ϕ
Fxy
y
Z = F sin θ , X = Fxy cos ϕ = F cos θ cos ϕ , Fxy是矢量吗? Y = Fxy sin ϕ = xF cos θ sin ϕ
B
ϕ
3m
y
Y3 = − 1500 cos θ sin ϕ = − 1073 N Z 3 = 1500 sin ϕ = 671 N
z 4m
AB 5 .5 9
3 5 4 = CB 5 =
60
A
o
D 2.5m
X
1
= 500 cos 90 o = 0
Y1 = 5 0 0 c o s 9 0 o = 0 Z 1 = 500 cos180 o = −500 N
空间力系沿坐标的分解与投影
空间力系 空间力的 分解 二次投影法 应用举例
A
空间力系
各力的作用线不在同一平面内 可分成
空间汇交力系 空间力偶系 空间任意力系(最一般的系)
与平面一般力系的不同
研究方法基本相同 概念、理论和方法要推广和引伸
B
空间力的分解
空间的力F
z
• 把其向各坐标轴分解 Z Fx,Fy,Fz •投影为 X=F cosα Y=F cosβ Z=F cosγ
x O
Fz Fx
C
E
γ
F
A
B
α
β
Fy
Dቤተ መጻሕፍቲ ባይዱ
y Y X
C
二次投影法
把力向z轴上投影 • 把力向oxy平面投影 • 把oxy平面上的投影
– 向x轴投影 – 向y轴投影
O z Z A C X E B
F
θ
Y
D
ϕ
Fxy
y
Z = F sin θ , X = Fxy cos ϕ = F cos θ cos ϕ , Fxy是矢量吗? Y = Fxy sin ϕ = xF cos θ sin ϕ
B
ϕ
3m
y
Y3 = − 1500 cos θ sin ϕ = − 1073 N Z 3 = 1500 sin ϕ = 671 N
z 4m
AB 5 .5 9
3 5 4 = CB 5 =
60
A
o
D 2.5m
X
1
= 500 cos 90 o = 0
Y1 = 5 0 0 c o s 9 0 o = 0 Z 1 = 500 cos180 o = −500 N
第1节力在直角坐标轴上的投影

F Fx Fy Fz Fxi Fy j Fzk
第 1 节 力在直角坐标轴上的投影
第三章 空间力系
• 已知力的三个投影,求力的大小和方向的公式
F Fx2 Fy2 Fz2
arccosFx
F
arccosFy
F
注意
arccosFz
F
力的投影和分量的区别:
力的投影是标量,而力的分量是矢量;
第 1 节 力在直角坐标轴上的投影
第三章 空间力系
设直角坐标系Oxyz
如图所示,已知力 F 与
x﹑y﹑z 轴间的夹角分别
z
为 ﹑ ﹑ 。则力 F 在
x﹑y﹑z 轴上的投影Fx﹑ Fz
F
Fy﹑Fz 分别为:
Fx F cos
Fx o
y
Fy F cos
x
Fy
Fz F cos
注意 Fx﹑Fy﹑Fz为代数量。
第 1 节 力在直角坐标轴上的投影
第三章 空间力系
例4-2 如图所示,在数控车床上加工外圆时,
已知被加工件S对车刀D的作用力(即切削抗力)的
三个分力为:Fx = 300 N,Fy = 600 N,Fz = 1500 N。 试求合力的大小和方向。
F Fz
Fx
S
Fy
D
第 1 节 力在直角坐标轴上的投影
F
1643
arccosFFz arccos11654030
arccos(0.9130 ) 155 o55
第三章 空间力系
解:取直角坐标系Oxyz如图所示。合力F 在 x、y、z 坐标轴上的分力为Fx、Fy 、Fz 。由于力在直角坐
标轴上的投影和力沿相应直角坐标轴的分力在数
值上相等,所以合力F 的大小和方向为
力投影-文档资料

F = Fcos x F = Fsin y
计算
二、要求
1、理解几种力系和力的投影的概念 2、理解力的投影的三种性质 3、能熟练计算力在直角坐标轴上的投影
作业
课本作业 教材P59 2-1 2-2
课外作业: (1)通过本内容的学习,你有哪些收获?还存在哪些困惑? (2)复习三角函数的有关知识,下次上课时要抽答
探究与感悟 (1)探究:建筑工程中的平、立、剖面图用的是什么投影?投影的 大小与实物间有何关系?建筑物的三维投视图运用了什么原理? (2)感悟: 1 在有月亮的晚上,看看自己的影子是变长了还是变短了,影子 的长短与什么因素有关? 2 感悟“人正不怕影子歪”的含义。
(3)平面力偶系:作用于同一个平面内的两 个或两个以上的力偶。 (4)平面一般力系:力的作用线全在同一平 面内任意分布的力系。(如下图所示)
二、力的投影
• 问题与思考 • 一根直立的电线杆,在一天的不同时间里 ,电线杆在地面上留下的影子长度是不同 的,这是为什么?
• 这是因为在不同时间段太阳光照射电线杆 的角度是不同的,因而电线杆留在地面上 的影子(即投影)长度也就随之变化。 • 那么,力在直角坐标轴上的投影该怎么求 呢?
• 结论:(力的投影性质) • (1)当力与坐标轴垂直时,力在该轴上的投影为零; • (2)当力与坐标轴平行时,其投影的绝对值与该力的大 小相等 • (3)当力平行移动后,在坐标轴上的投影不变。
• 力的投影计算举例
• 例:试求图中各力在 x、y轴上的投影。已知 F1= 100 N, F2= 150 N, F3= F4= 200 N。 • 解:Fx1= F1cos 45°= 100 ×0.707 = 70.7 N • Fy1= F1sin 45°= 100 ×0.707 = 70.7 N • Fx2= -F2cos 30°= -150 ×0.866 = -129.9 N • Fy2= F2sin 30°= 150 ×0.5 = 75 N • Fx3= F3cos 60°= 200 ×0.5 = 100 N • Fy3= -F3sin 60°= -200 ×0.866 • = -173.2 N • Fx4= F4cos 90°=0 • Fy4= -F4sin 90°= -200 ×1= -200 N
计算
二、要求
1、理解几种力系和力的投影的概念 2、理解力的投影的三种性质 3、能熟练计算力在直角坐标轴上的投影
作业
课本作业 教材P59 2-1 2-2
课外作业: (1)通过本内容的学习,你有哪些收获?还存在哪些困惑? (2)复习三角函数的有关知识,下次上课时要抽答
探究与感悟 (1)探究:建筑工程中的平、立、剖面图用的是什么投影?投影的 大小与实物间有何关系?建筑物的三维投视图运用了什么原理? (2)感悟: 1 在有月亮的晚上,看看自己的影子是变长了还是变短了,影子 的长短与什么因素有关? 2 感悟“人正不怕影子歪”的含义。
(3)平面力偶系:作用于同一个平面内的两 个或两个以上的力偶。 (4)平面一般力系:力的作用线全在同一平 面内任意分布的力系。(如下图所示)
二、力的投影
• 问题与思考 • 一根直立的电线杆,在一天的不同时间里 ,电线杆在地面上留下的影子长度是不同 的,这是为什么?
• 这是因为在不同时间段太阳光照射电线杆 的角度是不同的,因而电线杆留在地面上 的影子(即投影)长度也就随之变化。 • 那么,力在直角坐标轴上的投影该怎么求 呢?
• 结论:(力的投影性质) • (1)当力与坐标轴垂直时,力在该轴上的投影为零; • (2)当力与坐标轴平行时,其投影的绝对值与该力的大 小相等 • (3)当力平行移动后,在坐标轴上的投影不变。
• 力的投影计算举例
• 例:试求图中各力在 x、y轴上的投影。已知 F1= 100 N, F2= 150 N, F3= F4= 200 N。 • 解:Fx1= F1cos 45°= 100 ×0.707 = 70.7 N • Fy1= F1sin 45°= 100 ×0.707 = 70.7 N • Fx2= -F2cos 30°= -150 ×0.866 = -129.9 N • Fy2= F2sin 30°= 150 ×0.5 = 75 N • Fx3= F3cos 60°= 200 ×0.5 = 100 N • Fy3= -F3sin 60°= -200 ×0.866 • = -173.2 N • Fx4= F4cos 90°=0 • Fy4= -F4sin 90°= -200 ×1= -200 N
2.2力在坐标轴上的解析
O
y
A
θ B1 x
a
Fxy
b
其大小为: Fxy=Fcosθ
2.2.3 力在直角坐标轴上的投影
1.直接投影法:
已知力F 和各坐标轴
正向间夹角为α,β,γ
γ α β
(称为F的三个方向角)
则:力F在空间直角坐标轴上的投影为:
Fx Fcos Fy Fcos Fz Fcos
这称为直接投影法。
FR ( Fxi ) ( Fyi ) ( Fzi )
合力的方向:
2
cos( F , i ) Fxi / FR
cos( F , j ) Fyi / FR
1 2
R
cos( F , k ) Fzi / FR
作用线:必通过力系的汇交点。
特例:平面汇交力系:
在Oxy坐标系中,恒有:
FRz 0
F
zi
0
则平面汇交力系合力的大小:
FR ( Fxi ) 2 ( Fyi ) 2
合力的方向:
cos( F , i ) Fxi / FR
cos( F , j ) Fyi / FR
2.3.2 平衡的解析条件---平衡方程
1.空间汇交力系 汇交力系平衡的必要与充分条件是合力 FR等于零。 即:
2.平面汇交力系
令力系所在平面与oxy平面重合,则,
F 0
z
因此有:平面汇交力系的平衡方程为:
F F
x y
0 0
——平面汇交力系的平衡方程
小结: 空间汇交力系: 有三个独立平衡方程,可以 求解三个未知量; 平面汇交力系: 只有两个独立方程,只可以 求解两个未知量。
3. 求解汇交力系平衡问题的方法和步骤
y
A
θ B1 x
a
Fxy
b
其大小为: Fxy=Fcosθ
2.2.3 力在直角坐标轴上的投影
1.直接投影法:
已知力F 和各坐标轴
正向间夹角为α,β,γ
γ α β
(称为F的三个方向角)
则:力F在空间直角坐标轴上的投影为:
Fx Fcos Fy Fcos Fz Fcos
这称为直接投影法。
FR ( Fxi ) ( Fyi ) ( Fzi )
合力的方向:
2
cos( F , i ) Fxi / FR
cos( F , j ) Fyi / FR
1 2
R
cos( F , k ) Fzi / FR
作用线:必通过力系的汇交点。
特例:平面汇交力系:
在Oxy坐标系中,恒有:
FRz 0
F
zi
0
则平面汇交力系合力的大小:
FR ( Fxi ) 2 ( Fyi ) 2
合力的方向:
cos( F , i ) Fxi / FR
cos( F , j ) Fyi / FR
2.3.2 平衡的解析条件---平衡方程
1.空间汇交力系 汇交力系平衡的必要与充分条件是合力 FR等于零。 即:
2.平面汇交力系
令力系所在平面与oxy平面重合,则,
F 0
z
因此有:平面汇交力系的平衡方程为:
F F
x y
0 0
——平面汇交力系的平衡方程
小结: 空间汇交力系: 有三个独立平衡方程,可以 求解三个未知量; 平面汇交力系: 只有两个独立方程,只可以 求解两个未知量。
3. 求解汇交力系平衡问题的方法和步骤
2.1-2.2力在平面坐标轴上的投影
性质1:力偶无合力,本身又不平衡,是一个基本力学量。 力偶只能和力偶平衡,而不能和一个力平衡。 性质2:力偶中两个力在任意坐标轴上投影之代数和为零。 性质3:力偶中两力对任一点取矩之和恒等于力偶矩,而与 矩心的位置无关。
性质4:力偶可以在其作用面内任意移动或转动,而不影响它
对刚体的作用效应。
17
性质5:只要保持力偶矩大小和转向不变,可以任意改变力 偶中力的大小和相应力偶臂的长短,而不改变它对 刚体的作用效应。
FRy F1 y F2 y F3 y F4 y Fy
x
o
FRx F1x F2x
F4x F3x
FRx Fx
FRy Fy
合力投影定理:合力在任一轴上的投影,等于各分力在同一
轴上投影的代数和。
6
作业
P20 例2-1
为什么在离转动 轴不远的地方推门 , 用比较大的力才能把 门推开? 为什么在离转动 轴较远的地方推门 , 用比较小的力就能把 门推开?
用 (F,F')表示
F
d
F'
力偶的作 用面
力偶系:作用在刚体上的一群力偶。 力偶的作用效应:使刚体转动(由两个力共同作用引起)。 力的作用效应: 移动效应--取决于力的大小、方向;
转动效应--取决于力偶矩的大小、方向。
15
2、力偶矩
F
力偶臂 力偶的作 用面
d F' 力偶矩:m=±Fd
+ —
16
3、力偶的性质
利用合力矩定理:
求M O (F )
M O (Fx )+M O (Fy )=Fx b + Fy L a =F (Lsina +bcosa +asina )=M O (F )
理论力学-力的分解与力的投影以及平面力系中的力矩
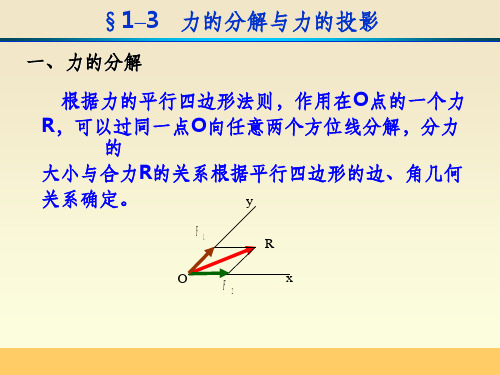
§ 1 –3
一、力的分解
力的分解与力的投影
根据力的平行四边形法则,作用在O点的一个力 R,可以过同一点O向任意两个方位线分解,分力的 大小与合力R的关系根据平行四边形的边、角几何 关系确定。
y
F1
O
R
F2
x
第一章
静力学的基本公理与受力分析
二、力在坐标轴上的投影
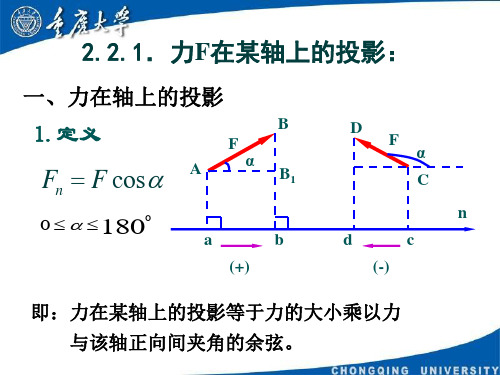
定义:在力矢量起点和终点作轴的垂线,在轴上得一线段,给 这线段加上适当的正负号,则称为力在轴上的投影。 F α
O
45
30
45
x
129.3 N
F3
Fy Fyi F1 sin 30 F2 sin 60 F3 sin 45 F4 sin 45 112.3 N
第一章 静力学的基本公理与受力分析
F4
例题
合力的大小:
平面基本力系
FR Fx2 Fy2 171.3 N
第一章 静力学的基本公理与受力分析
Fn Fr
例题
平面力系中的力矩
水平梁AB受三角形分布的载荷作用,如图所示。
载荷的最大集度为q, 梁长l。试求合力作用线的位置。
q
A B x
第一章
静力学的基本公理与受力分析
例题
解:
F
q
平面力系中的力矩
在梁上距 A 端为 x 的微段
dx上,作用力的大小为 q’ dx,
cos
Fy F
式中的α和β分别表示力F与x轴和y轴正向间的夹角。
第一章 静力学的基本公理与受力分析
合力投影定理
合力在任一轴上的投影等于各分力在同一轴上投影的代数和。
FR F1 F2 Fn F
一、力的分解
力的分解与力的投影
根据力的平行四边形法则,作用在O点的一个力 R,可以过同一点O向任意两个方位线分解,分力的 大小与合力R的关系根据平行四边形的边、角几何 关系确定。
y
F1
O
R
F2
x
第一章
静力学的基本公理与受力分析
二、力在坐标轴上的投影
定义:在力矢量起点和终点作轴的垂线,在轴上得一线段,给 这线段加上适当的正负号,则称为力在轴上的投影。 F α
O
45
30
45
x
129.3 N
F3
Fy Fyi F1 sin 30 F2 sin 60 F3 sin 45 F4 sin 45 112.3 N
第一章 静力学的基本公理与受力分析
F4
例题
合力的大小:
平面基本力系
FR Fx2 Fy2 171.3 N
第一章 静力学的基本公理与受力分析
Fn Fr
例题
平面力系中的力矩
水平梁AB受三角形分布的载荷作用,如图所示。
载荷的最大集度为q, 梁长l。试求合力作用线的位置。
q
A B x
第一章
静力学的基本公理与受力分析
例题
解:
F
q
平面力系中的力矩
在梁上距 A 端为 x 的微段
dx上,作用力的大小为 q’ dx,
cos
Fy F
式中的α和β分别表示力F与x轴和y轴正向间的夹角。
第一章 静力学的基本公理与受力分析
合力投影定理
合力在任一轴上的投影等于各分力在同一轴上投影的代数和。
FR F1 F2 Fn F
工程力学-2力的投影与平面力偶
0100 2 3 0200 2 2 054 N8
F R ( F x )2 ( F y )224 2 5 1 2 4 4 28 4 N75
tan0
Fy Fy
25441840.227
0 12.8
例2-4 图示支架由杆AB、BC组成,A、B、C处均为光滑铰链,在铰
B上悬挂重物G=10kN,杆件自重不计,试求杆件AB、BC所受的力。
y
解:1.取B销为研究对象画受力图
A
30°
B FAB
G
30° FCB
B G
2.建立坐标系列平衡方程
x Fy 0F B : C F B sC sG i3 i3 n n 0 0 2 G G 0 2 1 02k0N
例2-2
A
C
图示结构,在铰链B上作用力F,画结点B的受力图。
B FAB B F FCB F
解: 1.选B销为研究对象取分
离体。
2.在B销上画出主动力。
3.在B销上按约束力的画法画
出约束力。
AB杆为二力杆,约束力沿AB连线,
BC杆为二力杆,约束力沿BC连线,
◆ 课题2–1 力的投影 平面汇交力系的平衡 △
应用举例 例2-9 图示多孔钻床在气缸盖上钻四个圆孔,钻头作用工件的切
削力构成一个力偶,且力偶矩的大小M1=M2=M3=M4=-15N·m,转 向如图示。试求钻床作用于气缸盖上的合力偶矩MR。
解:取气缸盖为研究对象,其合 力偶矩为
M R M 1 M 2 M 3 M 4 1 4 5 6 N m 0
的力系均成立。若力系有n个力作用,即
M 0(F R) M 0(F )
求平面力对平面某点的力矩,一般采用以下两种方法:
F R ( F x )2 ( F y )224 2 5 1 2 4 4 28 4 N75
tan0
Fy Fy
25441840.227
0 12.8
例2-4 图示支架由杆AB、BC组成,A、B、C处均为光滑铰链,在铰
B上悬挂重物G=10kN,杆件自重不计,试求杆件AB、BC所受的力。
y
解:1.取B销为研究对象画受力图
A
30°
B FAB
G
30° FCB
B G
2.建立坐标系列平衡方程
x Fy 0F B : C F B sC sG i3 i3 n n 0 0 2 G G 0 2 1 02k0N
例2-2
A
C
图示结构,在铰链B上作用力F,画结点B的受力图。
B FAB B F FCB F
解: 1.选B销为研究对象取分
离体。
2.在B销上画出主动力。
3.在B销上按约束力的画法画
出约束力。
AB杆为二力杆,约束力沿AB连线,
BC杆为二力杆,约束力沿BC连线,
◆ 课题2–1 力的投影 平面汇交力系的平衡 △
应用举例 例2-9 图示多孔钻床在气缸盖上钻四个圆孔,钻头作用工件的切
削力构成一个力偶,且力偶矩的大小M1=M2=M3=M4=-15N·m,转 向如图示。试求钻床作用于气缸盖上的合力偶矩MR。
解:取气缸盖为研究对象,其合 力偶矩为
M R M 1 M 2 M 3 M 4 1 4 5 6 N m 0
的力系均成立。若力系有n个力作用,即
M 0(F R) M 0(F )
求平面力对平面某点的力矩,一般采用以下两种方法:
2.2力在坐标轴上的
再以B(或C)管为研究对象,画出其受力图。 选图示坐标系,列平衡方程
∑Fx=0,
得
F4-F1′cos60°=0
3 1 G 0.577kN 3 2
F4 F1cos60
考虑到管子每边在两端都各有一立柱,所以每根立柱所受 力的大小为
1 1 F F4 F4 0.289 kN 2 2
取投影轴x、y如图所示, 其中x轴沿CB方向, y轴垂直于FBC,列平衡方程
∑Fy=0, FABcos60°-FBDcos75°-Gcos30°=0 FAB=(FBDcos75°+Gcos30°)/ cos60° =G(cos75°+cos30°)/ cos60° =45.0kN(压力)
FAB =45.0kN(压力)
, ,
F4
e d Fx4 e, e,,
,
FRx Fxi
a
c
,
Fx3
a,,
FRx
合力在某个轴上的投影等于各个分力在同一 个坐标轴轴上投影的代数和.
2.3 汇交力系合成与平衡的解析法
2.3.1合成的解析法
1. 空间汇交力系
设空间汇交力系(F1,F2,…,Fn),其合
力为FR 。
FR Fi
O
y
A
θ B1 x
a
Fxy
b
其大小为: Fxy=Fcosθ
2.2.3 力在直角坐标轴上的投影
1.直接投影法:
已知力F 和各坐标轴
正向间夹角为α,β,γ
γ α β
(称为F的三个方向角)
则:力F在空间直角坐标轴上的投影为:
Fx Fcos Fy Fcos Fz Fcos
这称为直接投影法。
D
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
建筑力学 建筑力学基础
等待就是浪费青春
制:张启才
平面力系合成与平衡
2.1.1
力在平面坐标轴上的投影
投影 Fx
力F在坐标轴上的投影向量 即为坐标轴方向的分力。
投影数值:
X
F
Fx=Fcosa
Fy=Fcosb
b
a
Y
力在轴上的投影
当α、β为锐角时,FX、 Fy均为正值;
当α、β为钝角时,FX、 Fy可能为负值。
Fx F cosa
Fy F sin a
当投影Fx 、Fy 已知时,则可求出力 F 的大小和方向:
F Fx2
合力投影定理
合力在任一轴上的投影,等于它的各分力在 同一轴上的投影的代数和。
与投影轴同向为“+”、反向为“-
(1)力投影:代数量 力分量(分力):矢量 (2)力投影:无作用点 分 力:有作用点原力点
力在坐标轴上的投影
已知合力求分力公式:
FX FP cos a
FY FP sin a
已知分力求合力公式:
FP FX 2 FY 2
平面汇交力系的合成与平衡(解析法) 力在坐标轴上的投影可根据下式计算:
y
y
FF
y y
y y
F
F
O
F
Fy
O
Fy Fx
x x
Fy
O
Fx
x
O
Fx
x
Fx
x
分力Fx=?
(1)力 F在正交坐标轴 x、y上的投影量与 沿轴分解的分力大小相等; 讨论:力的投影与分量
(2)力F在不正交轴 x、y上的投影分量与 沿轴分解的分力大小不相等。 ——力在任一轴上的投影可求,分力并不确定
应注意
等待就是浪费青春
制:张启才
平面力系合成与平衡
2.1.1
力在平面坐标轴上的投影
投影 Fx
力F在坐标轴上的投影向量 即为坐标轴方向的分力。
投影数值:
X
F
Fx=Fcosa
Fy=Fcosb
b
a
Y
力在轴上的投影
当α、β为锐角时,FX、 Fy均为正值;
当α、β为钝角时,FX、 Fy可能为负值。
Fx F cosa
Fy F sin a
当投影Fx 、Fy 已知时,则可求出力 F 的大小和方向:
F Fx2
合力投影定理
合力在任一轴上的投影,等于它的各分力在 同一轴上的投影的代数和。
与投影轴同向为“+”、反向为“-
(1)力投影:代数量 力分量(分力):矢量 (2)力投影:无作用点 分 力:有作用点原力点
力在坐标轴上的投影
已知合力求分力公式:
FX FP cos a
FY FP sin a
已知分力求合力公式:
FP FX 2 FY 2
平面汇交力系的合成与平衡(解析法) 力在坐标轴上的投影可根据下式计算:
y
y
FF
y y
y y
F
F
O
F
Fy
O
Fy Fx
x x
Fy
O
Fx
x
O
Fx
x
Fx
x
分力Fx=?
(1)力 F在正交坐标轴 x、y上的投影量与 沿轴分解的分力大小相等; 讨论:力的投影与分量
(2)力F在不正交轴 x、y上的投影分量与 沿轴分解的分力大小不相等。 ——力在任一轴上的投影可求,分力并不确定
应注意
