数学期望与方差的运算性质
利用期望与方差的性质求期望或方差

9
方差
Var(X)=E[X-E(X)]2
刻划了随机变量的取值相对于其数学期望 的离散程度。
若X的取值比较集中,则方差较小; 若X的取值比较分散,则方差较大.
10
注意: 1) Var(X) 0,即方差是一个非负实数。 2)当X 服从某分布时,我们也称某分布的方差为Var(X)。 3) 方差是刻划随机变量取值的分散程度的一个特征。
6x)dx
3 10
E(Y 2 ) E( X 4 )
x4 f (x)dx
1x4 0
(6x2
6x)dx
1 7
D(Y ) E(Y 2 ) E 2 (Y ) 37 700
15
12
例1. 已知 X 的密度函数为
Ax2 Bx, 0 x 1,
f (x)
0,
其它
其中 A,B 是常数,且 E( X) = 0.5.
(1) 求 A,B. (2)设 Y=X2, 求 E(Y), D(Y).
13
解: (1)
f (x)dx
1
(
Ax 2
Bx)dx
2
注性质 4 的逆命题不来自立,即若E (X Y) = E(X)E(Y),X ,Y 不一定相互独立.
反例
pij
X
-1
0
1
Y
-1
18
18
18
0
1
18
0
18
18
18
18
pi•
38 28
38
p• j
38 28 38
3
XY
-1
0
1
P
概率分布中的期望与方差计算技巧

质量控制:在生产 过程中,方差用于 衡量产品质量的一 致性和稳定性,通 过控制产品质量指 标的方差来提高产
品质量
社会科学研究: 在社会科学研究 中,方差用于分 析调查数据的变 异性和不确定性, 以及比较不同样
本之间的差异
期望与方差在金融领域的应用
风险评估:用于衡量投资组合的风 险和预期收益
资本资产定价模型(CAPM):用 于确定资产的预期收益率,并评估 市场风险
定义:离散概率 分布的方差是各 个可能结果与期 望值的差的平方 的期望值。
计算公式:方差 = Σ (p(x) * (x μ)²),其中p(x) 是概率,μ是期 望值。
举例:假设一个随 机变量X只取两个 值,X=0的概率为 0.5,X=1的概率 为0.5,则方差 = (0.5 * (0 - μ)² + 0.5 * (1 - μ)²)。
添加标题
添加标题
添加标题
添加标题
资产定价:为金融资产(如股票、 债券等)定价,以确定其内在价值
投资组合优化:通过期望和方差等 参数,选择最佳投资组合以最大化 预期收益并最小化风险
感谢您的观看
汇报人:XX
方差的定义
方差是衡量数据点与平均值之间离散程度的统计量。
方差计算公式为:方差 = Σ((数据点 - 平均值)^2) / 数据点个数。
方差的值越小,说明数据点越接近平均值,离散程度越小;方差的值越大,说明数据点离散程度越 大。
方差在概率分布中表示随机变量取值的不确定性程度。
离散概率分布的方差计算
注意事项:可能不是整数
连续概率分布的期望值计算
定义:连续概率分 布的期望值是所有 可能取值的加权平 均值,其中每个取 值的权重为其概率 密度函数在该点的
常用分布的数学期望及方差

方差的性质
方差具有可加性
对于两个独立的随机变量X和Y,有Var(X+Y) = Var(X) + Var(Y)。
方差具有对称性
对于一个常数a和随机变量X,有Var(aX) = |a|^2 * Var(X)。
方差具有非负性
对于随机变量X,有Var(X) >= 0,其中 Var(X) = 0当且仅当X是一个常数。
05 数学期望与方差的应用
在统计学中的应用
描述性统计
数学期望和方差用于描述一组数据的中心趋势和 离散程度,帮助我们了解数据的基本特征。
参数估计
通过样本数据的数学期望和方差,可以对总体参 数进行估计,如均值和方差的无偏估计。
假设检验
在假设检验中,数学期望和方差用于构建检验统 计量,判断原假设是否成立。
常见分布的数学期望
均匀分布的数学期望为
$E(X) = frac{a+b}{2}$,其中a和b是均匀分布的下限和上 限。
柯西分布的数学期望为
$E(X) = frac{pi}{beta} sinh(frac{1}{beta})$,其中β是柯西 分布的参数。
拉普拉斯分布的数学期望为
$E(X) = frac{beta}{pi} tan(frac{pi}{beta})$,其中β是拉普 拉斯分布的参数。
03
泊松分布
正态分布是一种常见的连续型随机变量 分布,其方差记作σ²。正态分布的方差 描述了随机变量取值的分散程度。
二项分布是一种离散型随机变量分布, 用于描述在n次独立重复的伯努利试验 中成功的次数。其方差记作σ²,且σ² = np(1-p),其中n是试验次数,p是单次 试验成功的概率。
泊松分布是一种离散型随机变量分布, 用于描述在一段时间内随机事件发生的 次数。其方差记作σ²,且σ² = λ,其中 λ是随机事件发生的平均速率。
随机变量的数学期望和方差

随机变量的数学期望和方差随机变量是概率论中的重要概念,用来描述一个随机事件可能取到的不同值及其对应的概率。
对于一个随机变量而言,数学期望和方差是常用的统计量,用于描述随机变量的平均水平和离散程度。
一、数学期望数学期望是随机变量的平均值,表示了随机变量在大量重复实验中的长期平均表现。
通常用E(X)或μ来表示,其中X为随机变量。
对于离散型随机变量,数学期望的计算公式为:E(X) = ΣxP(X=x)其中,x为随机变量X可能取到的值,P(X=x)为其对应的概率。
以掷骰子为例,假设随机变量X表示掷骰子的点数,点数可能取到1、2、3、4、5、6,每个点数的概率相等。
则计算掷骰子的数学期望为:E(X) = 1/6 × 1 + 1/6 × 2 + 1/6 × 3 + 1/6 × 4 + 1/6 × 5 + 1/6 × 6 = 3.5对于连续型随机变量,数学期望的计算公式为:E(X) = ∫xf(x)dx其中,f(x)为随机变量X的概率密度函数。
二、方差方差是随机变量取值与其数学期望的偏差的平方的平均值,用于衡量随机变量的离散程度。
通常用Var(X)或σ^2来表示,其中X为随机变量。
对于离散型随机变量,方差的计算公式为:Var(X) = Σ(x-E(X))^2P(X=x)以掷骰子为例,假设随机变量X表示掷骰子的点数,其数学期望为3.5。
则计算掷骰子的方差为:Var(X) = (1-3.5)^2 ×1/6 + (2-3.5)^2 ×1/6 + (3-3.5)^2 ×1/6 + (4-3.5)^2 ×1/6 + (5-3.5)^2 ×1/6 + (6-3.5)^2 ×1/6 = 2.9167对于连续型随机变量,方差的计算公式为:Var(X) = ∫(x-E(X))^2f(x)dx方差的平方根被称为标准差,用于度量随机变量的离散程度。
数学期望(均值)、方差和协方差的定义与性质

均值、方差和协方差的定义和基本性质1 数学期望(均值)的定义和性质定义:设离散型随机变量X 的分布律为{}, 1,2,k k P X x p k === 若级数1k k k xp ∞=∑绝对收敛,则称级数1k k k xp ∞=∑的和为随机变量X 的数学期望,记为()E X 。
即()1k k k E X x p ∞==∑。
设连续型随机变量X 的概率密度为()f x ,若积分()xf x dx ∞−∞⎰ 绝对收敛,则称积分()xf x dx ∞−∞⎰的值为随机变量X 的数学期望,记为()E X 。
即 ()()E X xf x dx ∞−∞=⎰ 数学期望简称期望,又称为均值。
性质:下面给出数学期望的几个重要的性质(1)设C 是常数,则有()E C C =;(2)设X 是一个随机变量,C 是常数,则有()()E CX CE X =;(3)设X 和Y 是两个随机变量,则有()()()E X Y E X E Y +=+,这一性质可以推广至任意有限个随机变量之和的情况;(4)设X 和Y 是相互独立的随机变量,则有()()()E XY E X E Y =。
2 方差的定义和性质定义:设X 是一个随机变量,若(){}2E X E X −⎡⎤⎣⎦存在,则称(){}2E X E X −⎡⎤⎣⎦为X的方差,记为()D X 或()Var X ,即性质:下面给出方差的几个重要性质(1)设C 是常数,则有()0D C =;(2)设X 是一个随机变量,C 是常数,则有()()2D CX C D X =,()()D X C D X +=;(3)设X 和Y 是两个随机变量,则有()()()()()()(){}2D X Y D X D Y E X E X Y E Y +=++−−特别地,若X 和Y 相互独立,则有()()()D X Y D X D Y +=+ (4)()0D X =的充分必要条件是以概率1取常数()E X ,即(){}1P X E X ==。
数学期望和方差的性质

数学期望和⽅差的性质若随机变量 X 的分布⽤分布列 p (x i ) 或⽤密度函数 p (x ) 表⽰,则 X 的某⼀函数 g (X ) 的数学期望为E [g (X )]=∑i g x i p x i ,在离散场合∫∞−∞g (x )p (x )d x ,在连续场合 数学期望的性质若 c 是常数,则 E (c )=c .证明:如果将常数 c 看作仅取⼀个值的随机变量 X ,则有 P (X =c )=1 , 从⽽其数学期望 E (c )=E (X )=c ×1=c .对任意常数 a , 有 E (aX )=aE (X ) .证明:在 (1) 中令 g (x )=ax , 然后把 a 从求和号或积分号中提出来即得.对任意的两个函数 g 1(x ) 和 g 2(x ) 有E g 1(X )±g 2(X )=E g 1(X )±E g 2(X )证明:在 (1) 中令 g (x )=g 1(x )±g 2(x ) , 然后把和式分解成两个和式 , 或把积分分解成两个积分即得.⽅差的性质Var(X )=E X 2−[E (X )]2证明:Var(X )=E (X −E (X ))2=E X 2−2X ⋅E (X )+(E (X ))2=E X 2−2E (X )⋅E (X )+(E (X ))2=E X 2−[E (X )]2c 为常数, 则 Var(c )=0 .证明:Var(c )=E (c −E (c ))2=E (c −c )2=0若 a ,b 为常数 , 则 Var(aX +b )=a 2Var(X ) .证明:Var(aX +b )=E (aX +b −E (aX +b ))2=E (a (X −E (X )))2=a 2Var(X ){()()[][][]()()()()Processing math: 100%。
连续型随机变量的数学期望与方差
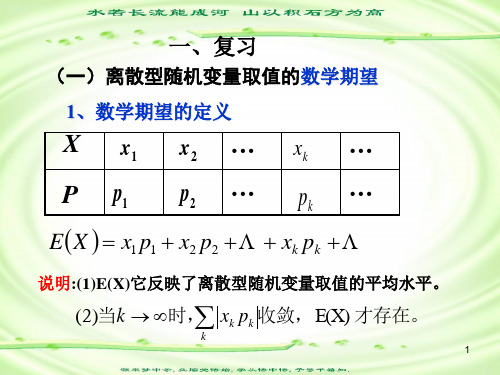
(1)D( )
E[
E( )]2
[x
E( )]2
p( x)dx
(2)方差的简便计算公式
D( )=E( 2) E(2 )
x2 p(x)dx
x p( x)dx
例2 随机变量的概率密度函数
6x(1 x),当0 x 1
p(x)
0
当x 0或x 1时
求随机变量的方差。
12
4、方差的性质 设 k ,b,c均为常数,则有
E( ) xp(x)dx
15
2、数学期望的性质
(1)EaX b aEX b
(2)EaX aEX
(3)EX b EX b
(4)Eb b
(5)EX Y EX EY
(6)E( f ( )) f (x)p(x)dx
(6)E f ( ) f (xk )PK
k
16
(二)连续型随机变量ξ取值的方差
(1)D(c) 0
(2)D(k ) k 2D( ) (3)D( b) D( )
(4)D(k b) k 2D( )
13
下页
三、练习
• 课本第90页 第6题
14
四、小结 (一)连续型随机变量ξ取值的数学期望
1、连续型随机变量的数学期望的定义 p(x) 设连续型随机变量 的密度函数为
若积分 xp(x绝)d对x 收敛,则 的数学期望为:
x0 x1 x2 L xn
xi xi1 xi
b i
【xi
,
xi
)
+1
y p(x)
o
x0b0 x1 xi bi xi1
xn x
6
连续型随机变量ξ的概率分布
ξ 【x0 , x1)【x1, x2)
期望与方差的概念及计算

期望与方差的概念及计算概率统计是应用最广泛的数学分支之一。
其中,期望和方差是两个极为重要的统计量。
他们体现了随机变量的特征和性质,为我们理解数据的特征提供了帮助。
本文将着重介绍期望和方差的概念及其计算方法。
一、期望的概念及计算期望,又称数学期望,是一个随机变量的平均值,其表现了样本空间中各种结果的权重平均值。
我们可以根据随机变量的取值和概率来求期望。
对于离散型随机变量,期望的计算公式为:E(X)=∑xiPi其中,xi是随机变量取得的各个值,Pi是相应的概率。
将每个xi乘以其对应的Pi,再求和,就可以得到该离散型随机变量的期望。
对于连续型随机变量,期望的计算公式为:E(X)= ∫xf(X)dx其中,f(X)是随机变量的概率密度函数。
同样,我们需要将随机变量的每个取值乘以该取值的密度函数值,再在整个样本空间上对其进行积分,即可得到该连续型随机变量的期望。
二、方差的概念及计算方差是随机变量与其期望之间偏离程度的一个度量。
方差越大,说明随机变量分布的波动范围越大。
方差的公式为:Var(X)= E[(X- μ)2] = E(X2)- [E(X)]2其中,μ是随机变量的期望值。
这个公式看起来比较复杂,我们可以简单地理解为:计算随机变量的每个取值与期望的距离的平方,再将这些平方值加起来,再除以总共的取值个数,就得到了方差的值。
那么,如何计算每个取值与期望的距离呢?我们可以借助离差的概念来处理这个问题。
离差,指的是随机变量每个取值与其期望值的差值。
利用离差的概念,我们可以将方差公式写为如下形式:Var(X)= ∑ (xi-μ)2Pi同样,对于连续型随机变量,其方差的计算公式为:Var(X)= ∫ (x-μ)2f(X)dx三、期望和方差的性质期望和方差是随机变量与概率密度函数之间的一个重要关系。
它们有以下几个基本性质:1. 常数的期望等于这个常数。
2. 线性组合的期望等于各个随机变量的期望的线性组合。
3. 期望的加法分配律。
