第六章研究生数值分析
合集下载
数值分析第六章课件
a(1) 1n
x1
b(1) 1
a(1) 21
a(1) 22
a(1) 2n
x2
b(1) 2
.
a(1) m1
a(1) m2
a(1) mn
xn
b(1) m
将(2.1)记为A(1)x=b(1)，其中
a(1) 11
a(1) 12
a(1) 1n
a11
a12
a1n
A(1)
a(1) 21
5.2 高斯消去法
本节介绍高斯消去法(逐次消去法)及消去法和 矩阵三角分解之间的关系. 虽然高斯消去法是一种 古老的求解线性方程组的方法(早在公元前250年 我国就掌握了解方程组的消去法)，但由它改进、 变形得到的选主元素消去法、三角分解法仍然是目 前计算机上常用的有效方法.我们在中学学过消去 法,高斯消去法就是它的标准化的、适合在计算机 上自动计算的一种方法.
有的问题的数学模型中虽不直接表现为含线性方 程组,但它的数值解法中将问题“离散化”或“线性 化”为线性方程组.因此线性方程组的求解是数值分 析课程中最基本的内容之一.
关于线性方程组的解法一般有两大类：
1. 直接法 经过有限次的算术运算,可以求得方程组的精确解( 假定计算过程没有舍入误差).如线性代数课程中提到 的克莱姆算法就是一种直接法.但该法对高阶方程组 计算量太大,不是一种实用的算法.
下面讨论求解一般线性方程组的高斯消去法.由
a11 x1 a12 x2 a1n xn b1 a21 x1 a22 x2 a2n xn b2
am1 x1 am2 x2 amn xn bm
a(1) 11
a(1) 21
x1 x1
a(1) 12
x2
数值分析研究生
(4) 若系数矩阵对称正定, 则G-S法, SOR法(0<<2)收敛.
2. 掌握并会应用迭代法的误差估计式
第四章 解非线性方程的迭代法 基本知识点 1. 会判断有根区间; 会建立简单迭代法迭代格式; 会判定迭
代方法的收敛性.(定理4.1)
2. 掌握迭代法收敛阶的概念, 会求迭代法的收敛阶 (勿混). 3. 会建立Newton迭代格式; 知道其优点和局限性(定理4.3). f (x)在根的邻域内有二阶连续导数, 且f ()0, 则Newton 迭代法在根的某个邻域上收敛, 收敛阶(至少)为2. 4. 了解Newton迭代法的变形方法的有关思想和收敛性.
3. 掌握复化(梯形、Simpson)求积公式及误差(勿混).
4. 了解Gauss型求积公式的基本性质及构造思路.
思路1: 教材P211; 思路2: 教材P190 5. 理解差商型数值微分公式的思想和4个常用格式.
第八章 常微分方程数值解法 基本知识点
1. 能利用Lipschitz条件判别常微分方程初值问题是否存在
返回第四章知识点
几个常用的数值求积公式及误差 1) 梯形公式
b
b
a
ba (b a)3 f ( x)dx [ f (a) f (b)] f ( ) 2 12
2) Simpson公式
a
ba ab (b a) ( 4) f ( x)dx [ f (a) 4 f ( ) f (b)] f ( ) 6 2 2880
• 注意控制答题进度，有效利用考试时间。 • 大型计算题或论述题要按步骤规范答题。
• 事先可对考题的难易程度做出不同的预案。不骄不躁。
• 每一分的努力都有价值，切忌“留白”。空白=0分！
研究生数值分析 讲义
第一章绪论上次课要点：§1 数值分析的几个基本问题一、用数学方法解决科学与工程问题的步骤二、研究对象三、研究内容四、研究数值计算方法的意义五、算法设计的基本思想六、算法应具备的特性§2 数值计算的误差一、误差的分类 1．截断误差 2．舍入误差二、误差的概念 1．绝对误差x x x E -=**)(2．相对误差xx E x E r )()(**=（其中0≠x ）本次课继续。
三、数值运算的误差当自变量有误差时，一般地，其函数值也有误差。
误差——可能是截断误差——也可能是舍入误差1．一元函数的误差设*x 是准确值x 的近似值，则函数)(x f 的近似值为)(*x f 。
由于))(()()(**x x f x f x f -'=-ξ，ξ介于x 与*x 之间，所以)()()()(**x x f x f x f -'=-ξ从而)()())((**x f x f εξε'≈2. 多元函数的误差对于多元函数),,,(21n x x x f ，设自变量的近似值分别为**2*1,,,nx x x ，则),,,(),,,(),,,((21**2*1**2*1n nnx x x f x x x f x x x f E -=)(|)(|*),,,(*1),,,(1**2*1**2*1nx x x nx x x x e x f x e x f nn∂∂++∂∂≈于是误差限),,,((**2*1nx x x f ε∑=∂∂≈nk kx x x kx x f n1*),,()(|**2*1ε特别)()()(*2*1*2*1x x x x εεε+≈±)()()(*1*2*2*1*2*1x x x x x x εεε+≈2*2*1*2*2*1*2*1)()()/(xx x x x x x εεε+≈四、病态问题与条件数一个工程或科学计算问题：——往往需要巨量的机器运算——每次运算都可能产生误差——这些误差有正有负，绝对值有大有小误差积累的结果很难定量分析。
数值分析课件 (第5、6章)
(1 ( La1n) b11) (2) (2) a L 2n b2 = A(3) : b(3) LM M (3) (3) Lamn bn
[
]
( ( ( aij3) = aij2) −mij a22) j (3) ( bi = bi(2) −mi2b22)
(i = 3,L m j = 3,L n) , ; , (i = 3,L m) ,
[
]
( ( ( aij2) = aij1) − mij a11) j (2) bi = bi(1) − mi1b(1) 1
研究生公共课程数学系列
(i = 2,L m j = 2,L n) , ; , (i = 2,L m) ,
机动 上页 下页 首页 结束
(2)
[A
(2)
: b(2)
]
(1 (1 a11) a12) (2 0 a22) = M M (2) 0 am2
(n)
续 述 程 到 成 s 消 计 。 继 上 过 , 直 完 第步 元 算
后 到 原 程 等的 单 程 A 最 得 与 方 组 价 简 方 组 (s+1) x = b,(s+1) 中（ ） 上 形 其 A s+1 为 梯 。
(1 (1 (1 a11) a12) L a1n) (2 ( a22) L a22) n = O M (n ann)
( a2k ) k m = (k ) ik akk
(k (akk ) ≠0)
−−−−−→
(i=k+1,Lm) ,
(1 (1 ( a11) a12) L a11) k (2 ( a22) L a22) k O M (k akk ) M 0
数值分析第六章_ppt课件
j
12 j i n n
% | D l = l ( e ) a | = e , j = 1 , 2 , L , n j| j
1 n
E 设 10,n 20 , 则 101 .若 在 A 的上三角位置，则特征值并无扰动.
湘潭大学数学与计算科学学院 上一页 下一页 8
定理3 设 A 为 n阶实对称矩阵，其特征值
为 1 2 n，则
n x 0
1 x 0
m i n R ( x ) m i n ( A x , x )
m a x R ( x ) m a x ( A x , , x )
通过求它的根来求矩阵的特征值,实际计算中并不采用。
数值方法 基本思想: 直接从矩阵A 或者对A 做一系列的 相似变换后得到的具有更简单形式的矩阵入手,
设计迭代过程;最后求得A 的近似特征值和相应
的特征向量.
湘潭大学数学与计算科学学院
上一页
下一页
4
特征值的估计及扰动问题
1、特征值的估计
D ( A ) { z c :| z a | | a | }, i 1 , 2 , ,n i ii ij i
为矩阵 A关于向量 x 的Rayleigh（雷利）商.
A 为 n 阶实对称矩阵，则其特征值皆为实数，
记做
1 2
， n
并且存在规范正交特征向量系满足：
Au u ,i 1 , 2 , , n , ( u , u ) ,i , j 1 , 2 , , n i i i i j ij
3 4
湘潭大学数学与计算科学学院
上一页
下一页
7
实对称矩阵的极大-极小定理：
12 j i n n
% | D l = l ( e ) a | = e , j = 1 , 2 , L , n j| j
1 n
E 设 10,n 20 , 则 101 .若 在 A 的上三角位置，则特征值并无扰动.
湘潭大学数学与计算科学学院 上一页 下一页 8
定理3 设 A 为 n阶实对称矩阵，其特征值
为 1 2 n，则
n x 0
1 x 0
m i n R ( x ) m i n ( A x , x )
m a x R ( x ) m a x ( A x , , x )
通过求它的根来求矩阵的特征值,实际计算中并不采用。
数值方法 基本思想: 直接从矩阵A 或者对A 做一系列的 相似变换后得到的具有更简单形式的矩阵入手,
设计迭代过程;最后求得A 的近似特征值和相应
的特征向量.
湘潭大学数学与计算科学学院
上一页
下一页
4
特征值的估计及扰动问题
1、特征值的估计
D ( A ) { z c :| z a | | a | }, i 1 , 2 , ,n i ii ij i
为矩阵 A关于向量 x 的Rayleigh（雷利）商.
A 为 n 阶实对称矩阵，则其特征值皆为实数，
记做
1 2
， n
并且存在规范正交特征向量系满足：
Au u ,i 1 , 2 , , n , ( u , u ) ,i , j 1 , 2 , , n i i i i j ij
3 4
湘潭大学数学与计算科学学院
上一页
下一页
7
实对称矩阵的极大-极小定理：
《数值分析》第六章
由上述 Th 1 可知， 迭代过程 xk +1 = ϕ ( xk ) 对于任 x ∈ Δ 意的初值 0 均收敛.
有局部收敛性.
证 明 . 由 连 续 函 数 的 性 质 ， 存 在 x* 的 邻 域
Δ : x − x* ≤ δ
，使 ∀x ∈ Δ 成立 ϕ '( x) ≤ L < 1 ，此外，
对于任意 x ∈ Δ ，总有 ϕ ( x) ∈ R ，这是因为
15 16
迭代法不一定收敛. 对同一个问题，不同的迭代法， 可能有的收敛，有的不收敛. 如下例.
Th 1 假定函数 ϕ (x) 满足： 1 对任意 x ∈ [a, b] 有， ϕ ( x) ∈ [a, b] （即，映像入内）
∀x ∈ [a, b] ， ϕ '( x ) ≤ L < 1 2 存在非负数 L < 1 使得， （压 缩映射）
k → ∞ 时成立下列渐近关系式
= xk − x * 当
求根 x * 的邻近连续，并且满足：
ϕ '( x* ) = ϕ ''( x* ) = L = ϕ ( p −1) ( x * ) = 0 ， ϕ ( p ) ( x * ) ≠ 0
ek +1 → C ( C ≠ 0) e kp
则称该迭代过程是 p 阶收敛的. 特别地， p = 1 时称为线性收敛，
*
* *
* * 假设 x , y ∈ [a, b] 是任意的两个根，因为
xk = x * . 故 lim k →∞
x* − y* = ϕ ( x* ) − ϕ ( y* ) = ϕ '(ξ )( x* − y* ) ≤ L x* − y*
* * 故 x = y , 即， x = ϕ ( x ) 在[a,b]上有唯一的根.
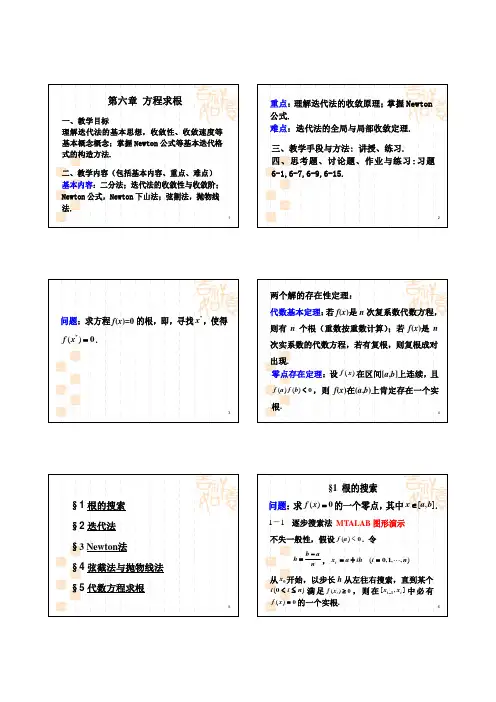
有局部收敛性.
证 明 . 由 连 续 函 数 的 性 质 ， 存 在 x* 的 邻 域
Δ : x − x* ≤ δ
，使 ∀x ∈ Δ 成立 ϕ '( x) ≤ L < 1 ，此外，
对于任意 x ∈ Δ ，总有 ϕ ( x) ∈ R ，这是因为
15 16
迭代法不一定收敛. 对同一个问题，不同的迭代法， 可能有的收敛，有的不收敛. 如下例.
Th 1 假定函数 ϕ (x) 满足： 1 对任意 x ∈ [a, b] 有， ϕ ( x) ∈ [a, b] （即，映像入内）
∀x ∈ [a, b] ， ϕ '( x ) ≤ L < 1 2 存在非负数 L < 1 使得， （压 缩映射）
k → ∞ 时成立下列渐近关系式
= xk − x * 当
求根 x * 的邻近连续，并且满足：
ϕ '( x* ) = ϕ ''( x* ) = L = ϕ ( p −1) ( x * ) = 0 ， ϕ ( p ) ( x * ) ≠ 0
ek +1 → C ( C ≠ 0) e kp
则称该迭代过程是 p 阶收敛的. 特别地， p = 1 时称为线性收敛，
*
* *
* * 假设 x , y ∈ [a, b] 是任意的两个根，因为
xk = x * . 故 lim k →∞
x* − y* = ϕ ( x* ) − ϕ ( y* ) = ϕ '(ξ )( x* − y* ) ≤ L x* − y*
* * 故 x = y , 即， x = ϕ ( x ) 在[a,b]上有唯一的根.
数值分析(李庆扬)第六章资料
（n1） B （n） g
若收敛
x x { （k）} * ，则
x* Bx* g
n 0，1，2，
即
(I B)x* g D1Ax* D1b
Ax* b
故如果序列收敛, 则收敛到解.B 称迭代矩阵.
例：用Jacobi迭代法求解 1x01x1 10xx2222xx337823 x1 x2 5x3 42
k
k
即x是方程组Ax b的解。
引入误差向量
(k 1) x(k 1) x
所以 lim x(k) x 等价于 lim (k) 0
k
k
由
x(k 1) Mx (k ) g
x Mx g
则可得
(k 1) M (k )
(k ) M (k 1) M k (0)
问题是在什么条件下
满足
x(k1) Bx(k) g (k 0,1, 2, )
此过程所给出的迭代法称为Jacobi迭代法，又称简单
迭代法。
Jacobid迭代的矩阵形式
0
B
b21
b12
0
b1n 1
b2n
0
0 1
0 1
0
b21
b 12 1
b1n b 2n
b b
n1
n2
0
0
0
1
, n).
0 b12 b13 若记 B b21 0 b23
bn1 bn2 bn3
b1n1 b1n
g1
b2n1
b2
n
g
g
2
bnn1 0
gn
则方程组可简记为 x Bx g
选初值向量x(0)代入 x(1) , x（1） Bx（0） g，代入x(1)
研究生数值分析课件ch
详细描述
数值分析是数学的一个重要分支，主要研究如何利用数值方法求解数学问题和近似计算 实际问题的数值解。它为科学研究、工程技术和实际应用等领域提供了重要的数学工具。 数值分析的重要性在于它能够将许多抽象的数学概念和理论转化为具体的数值计算方法，
使得我们能够更加方便地解决各种复杂的实际问题。
数值分析的应用领域
在金融领域，数值分析也被 广泛应用于风险评估、投资 组合优化、期权定价等方面 。通过数值分析的方法，我 们可以更加准确地评估投资 风险和收益，从而做出更加 明智的决策。
数值分析的发展历程
总结词
数值分析的发展历程可以追溯到上世纪初，随着计算 机技术的不断发展，数值分析的理论和方法也在不断 更新和完善。
05
数值积分与微分
牛顿-莱布尼兹公式与复化求积法
牛顿-莱布尼兹公式
该公式是微积分中的一个基本定理，用于计算定积分。 通过将积分区间分成若干小区间，并在每个小区间上应 用微积分基本定理，再利用定积分的线性性质进行求和 ，最后取极限得到定积分的值。
复化求积法
当被积函数是复杂函数或者积分区间是复杂形状时，直 接应用牛顿-莱布尼兹公式可能会遇到困难。此时，可以 采用复化求积法，即将积分区间分成若干个小区间，然 后在每个小区间上应用牛顿-莱布尼兹公式，最后将所有 的结果相加得到定积分的近似值。
改进欧拉法
为了提高欧拉方法的精度，可以对欧拉方法进行改进。一种常见的改进方法是使用二阶 欧拉方法，它考虑了更多的函数值，从而提高了逼近的精度。
龙格-库塔方法
龙格-库塔方法是一种高阶数值方法，用于求解常微分方程。它基于泰勒级数的思想，通过迭代的方式逐步逼近方程的精确解 。与欧拉方法相比，龙格-库塔方法具有更高的精度和更好的稳定性。
数值分析是数学的一个重要分支，主要研究如何利用数值方法求解数学问题和近似计算 实际问题的数值解。它为科学研究、工程技术和实际应用等领域提供了重要的数学工具。 数值分析的重要性在于它能够将许多抽象的数学概念和理论转化为具体的数值计算方法，
使得我们能够更加方便地解决各种复杂的实际问题。
数值分析的应用领域
在金融领域，数值分析也被 广泛应用于风险评估、投资 组合优化、期权定价等方面 。通过数值分析的方法，我 们可以更加准确地评估投资 风险和收益，从而做出更加 明智的决策。
数值分析的发展历程
总结词
数值分析的发展历程可以追溯到上世纪初，随着计算 机技术的不断发展，数值分析的理论和方法也在不断 更新和完善。
05
数值积分与微分
牛顿-莱布尼兹公式与复化求积法
牛顿-莱布尼兹公式
该公式是微积分中的一个基本定理，用于计算定积分。 通过将积分区间分成若干小区间，并在每个小区间上应 用微积分基本定理，再利用定积分的线性性质进行求和 ，最后取极限得到定积分的值。
复化求积法
当被积函数是复杂函数或者积分区间是复杂形状时，直 接应用牛顿-莱布尼兹公式可能会遇到困难。此时，可以 采用复化求积法，即将积分区间分成若干个小区间，然 后在每个小区间上应用牛顿-莱布尼兹公式，最后将所有 的结果相加得到定积分的近似值。
改进欧拉法
为了提高欧拉方法的精度，可以对欧拉方法进行改进。一种常见的改进方法是使用二阶 欧拉方法，它考虑了更多的函数值，从而提高了逼近的精度。
龙格-库塔方法
龙格-库塔方法是一种高阶数值方法，用于求解常微分方程。它基于泰勒级数的思想，通过迭代的方式逐步逼近方程的精确解 。与欧拉方法相比，龙格-库塔方法具有更高的精度和更好的稳定性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
∑x
n
m
i
(2)确定近似表达式
设拟合曲线为二次多项式 y = P2 ( x ) = a0 + a1 x + a2 x 2
(3)建立正则方程组 n = 7,
4 6 7 8 2 3 6 7 5 3 2
n n ∑ xi i =1 n 2 ∑ xi i =1
最小 1
特别地 , 一次 ( 线性 )最小二乘拟合多项式求 解公式 :
2、 使 残 差 的 平 方 和 最 小 , 即
∑ δ i2 = δ
i =1
2
最佳平方逼近 最小二乘拟合
最小 2
3、 使 残 差 的 最 大 绝 对 值 最 小 , 即
n n ∑ xi i =1 n S x
x i = 31, ∑ xi2 = 179, ∑ i =1 i =1 xi4 = 8147, ∑ i =1
7
7
n ∑ yi a0 i = 1 n n xi3 a1 = ∑ xi yi ∑ i=1 a i =1 n 2 n 2 xi4 ∑ xi yi ∑ i =1 i= 1
n 2 i
∑ xi3 = 1171,
i =1 7
∑ yi = 28,
i =1
∑ xi yi = 121,
i =1
7
yi xi2 = 635, ∑ i =1
7
16
Printed with FinePrint - purchase at PDF 文件使用 "pdfFactory Pro" 试用版本创建
§1 数据拟合的最小二乘法 第六章习题 P162, 1, 3, 4, 6, 13(2)
1.1 多项式拟合
已知数据组( xi , yi )( i = 1, 2, L , n)，
n
xi yi
x1 y1
2
x2 L x n y2 L yn
如果m次多项式Pm ( x ) = a0 + a1 x1 + a2 x 2 + Lam x m , 使得
3
称此方程组为正则方程法方程组
7
求逼近函数 ϕ ( x )的常用规则： 1、 使 残 差 的 绝 对 值 和 最 小 , 即
结论：正则方程组存在唯一解， 且解所对应的多项式为 已知数据组 ( x i , y i ) ( i = 1,2,L , n)的最小二乘 m 次拟合多项式 .
∑
n
n
i=1
δi = δ
1 x2
m x2
L L
M
1 y1 xn y2 M M m L xn yn
11
点的分布近似为抛物线
15
n n x i ∑ i =1 M n xm ∑ i i =1
∑x ∑x
i =1 i =1 n i
n ∂F m 2 = 2∑ yi − (a0 + a1 xi + a2 xi + Lam xi ) ( − xi ) = 0 ∂a1 i =1
整理得
na0 + a1 ∑ xi +a2 ∑ xi 2 + L+ am ∑ xi m = ∑ yi
i =1 i =1 i =1 i =1
n
n
n
n
n
i 2
∑x
i =1
n
M
m +1 i
n ∑ yi i =1 i =1 a0 n n m +1 a L ∑ xi 1 y x = ∑ i i =1 i =1 M M M n n a m m 2m y i xi L ∑ xi ∑ i =1 i =1 L
由多元函数取极值的必要条件 ,
n ∂F 2 m =0 2∑ yi − (a0 + a1 xi + a2 xi + Lam xi ) ( − 1) = 0 ∂a0 i =1
插值 求一近似函数 ϕ ( x ), 使其尽可能 " 好 " 地 反映数据点的基本趋势 .
2
LLLLL n ∂F 2 m m = 2∑ yi − (a0 + a1 xi + a2 xi + Lam xi ) ( − xi ) = 0 ∂am i =1
当m > n时为超定方程组 , 其最小二乘解
列 xi yi xi2 x i yi
数 据 表: 1 2 3 0.5 2.5 2.0 1 4 9 0.5 5.0
4 4.0 16
5 3.5 25
6 6.0 36
7 5.5 49
S x = 28 S y = 24.0 S xx = 140
6.0 16.0 17.5 36.0 38.5 S xy = 119.5
1 2 3 0.5 2.5 2.0
S xx = 140 1 4 9 16 25 36 49 0.5 5.0 6.0 16.0 17.5 36.0 38.5 S xy = 119.5
13
超定线性方程组的最小二乘解
a 11 x 1 + a 12 x 2 + L a 1 n x n = b1 a 21 x 1 + a 22 x 2 + L a 2 n x n = b 2 L a m 1 x 1 + a m 2 x 2 + L a mn x n = b m
31 179 a0 7 31 179 1171 a = 得正则方程组为 1 179 1171 8147 a2 (4) 求解正则方程组得
28 121 635
求已知数据组形如 y = be ax的最小二乘拟合函数 .
6
已知数据表 ( x i , y i )( i = 1,2, L , n )， 近似函数为 ϕ ( x )
求最小二乘拟合 m次多项式 ,即求下列函数的极小值点
2 m F (a0 , a1 L am ) = ∑ y i − (a 0 + a 1 x i + a 2 x i + L a m x i ) i =1 n 2
n i ∑ yi i =1 0 = = i =1 n n 2 a1 xi ∑ ∑ xi y i i =1 i= 1
∑ x a
n
m ax δ i = δ
1≤ i ≤ n
∞
最小
最佳一致逼近
4
Sy S x a0 == S xx a1 S xy
残差：
δ i = yi − ϕ ( xi ) (i = 1,2,L, n)
残差向量：
δ = (δ1 ,δ2 ,Lδ n )
由多元函数取极值的必要条件 ,
n n n n m 2 na0 + a1 ∑ xi +a2 ∑ xi + L+ am ∑ xi = ∑ yi i =1 i =1 i =1 i =1 n n n n n m +1 2 3 a0 ∑ xi + a1 ∑ xi + a2 ∑ xi + L+ am ∑ xi = ∑ yi xi i =1 i =1 i =1 i =1 i =1 LLL n n n n n m a0 ∑ xi + a1 ∑ xi m +1 + a2 ∑ xi m + 2 + L+ am ∑ xi 2m = ∑ yi xi m i =1 i =1 i =1 i =1 i =1
是正则方程组的 AT Ax = AT b的解 .
a1 = 0.8393
14
此数据表的一次最小二乘拟合多项式为 : P1 ( x ) = 0.0714 + 0.8393 x
例 : 给定 一组实验数据如下 xi yi 1 2 2 3 3 6 4 7 6 5 7 3 8 2
求数据表( xi , yi )( i = 1,2,L , n),的最小二乘拟合m次多项式 等价于求超定方程组的最小二乘解, a 0 + a 1 x 1 + L a m x 1m = y1 m a 0 + a1 x 2 + L a m x 2 = y 2 n> m +1 L m a 0 + a1 x n + L a m x n = yn 正则方程组为 :
n 2 i
yi
求它的最小二乘一次拟合多项式 . 解 : 列数据表
xi yi xi2 xi yi
9
n S x
4 4.0 5 3.5 6 6.0
Sy S x a0 == S xx a1 S xy
7 5.5 S x = 28 S y = 24.0
例 : 已知数据表 xi
n
1 0.5
2 2.5
3 2.0
4 4.0
5 3.5
6 6.0
7 5.5
∑x ∑x
i =1 n i
n
∑x
i =1 n
2 i
∑x
i =1
3 i
∑ yi i =1 a0 i = 1 n n 3 xi a1 = ∑ x i y i ∑ i =1 a i = 1 2 n n 2 xi4 ∑ xi yi ∑ i =1 i =1
1
n
2
即求F (a0 , a1 ,Lam )的最小值点
n
i =1
5
第六章
函数逼近