19.1变量与函数(1)导学案
《19.1.1 变量与函数》教案1
《变量与函数》（第一课时）设计单位：黑松驿初级中学八年级数学第十九章《一次函数》19.1《函数》19.1.1变量与函数第一课时（变量与常量）知识目标：理解变量与常量的概念。
重点：变量与常量的概念，变量之间的关系难点：对变量的判断教学设计：一.创设情景，引入新课（1）同学们，你们用过电话吗？假如每分钟的电话费为0.20元，那么我们在打电话的过程中，电话总费用M与通话时长t具有怎样的关系．提问：上述问题中，哪个量是固定不变的，哪些量又是可以变化的？二.讲授新课出示定义：在一个变化过程中，我们称数值发生变化的量为变量.数值始终不变的量为常量.（2）每张电影票的售价为10元，如果第一场售出票150张，第二场售出票205张，第三场售出票310张，三场电影的票房收入各多少元？设一场电影受出票x张，票房收入为y元，怎样用含x的式子表示y？（3）当圆的半径为r分别为10厘米，20厘米，30厘米时，圆的面积S分别是多少？S与r有怎样的关系？Ｓ的值随ｒ的值得变化而变化吗？提问：请同学们指出上述问题中的变量和常量.学生活动：写出下列各问题中所满足的关系式，并指出各个关系式中，哪些量是变量，哪些量是常量？1. 小明到商店买练习本，每本单价2元，购买的总数x （本）与总金额y（元）有怎样的关系2. 盛满10千克水的水箱，每小时流出0.5千克水，则水箱中的余水量y(千克)与时间t（小时）之间的关系如何表示呢？３.一只蜡烛全长20厘米，点燃后每分钟燃烧0.2厘米。
燃烧时间t，蜡烛剩余部分L。
用含t的式子表示L４、小明的哥哥是一名大学生，他利用暑假去一家公司打工，报酬16元/时计算，设小明的哥哥这个月工作的时间为t 时，应得报酬为m 元，则m与t有怎样的关系？你能找出其中的变量与常量吗？5.长方形的面积为10平方米，那么它的长X与宽y具有怎样的关系。
你能找出其中的变量与常量吗？6.大米的单价为2.50元/千克，则购买的大米的数量x（kg）与金额与金额y的关系.三、巩固练习1、学生叙述生活中的情景，并找出常量和变量2、投影变量与常量的练习题（试情况而定）四、课堂小结变量：在一个变化过程中数值发生变化的量常量：在一个变化过程中数值始终保持不变的量五、作业1.现有笔记本500本，学生x人，若每人5本，则余下y本笔记本，用含x的式子表示y为：y=________，其中常量是_____，y和x都是_____量.2.小张准备将平时的零用钱节约一些储存起来．他已存有50元，从现在起每个月末存12元．设x个月后小张的存款数为y,试写出小张的存款数y与从现在开始的月份数x之间的函数关系式，其中常量是，变量是.六、课后反思。
19.1.1变量与函数--新人教版初中数学导学案八年级上册《一次函数》【一流精品】
课题：19.1.1变量与函数【学习目标】1、理解变量、常量，函数、自变量和函数值，函数解析式、自变量的取值范围等概念；2、会根据定义判断一个变量是否为另一个变量的函数；3、会根据相等关系列出函数关系式，并会据实际意义求出自变量的取值范围； 【学习重点】据相等关系列函数关系式，求自变量的取值范围。
【学习难点】判断一个变量是否为另一个变量的函数。
【课前预习案】1、时间t 、速度v 和路程s 三者之间的关系是：2、半径为r 的圆的面积s=3、当x 是怎样的实数时，下列各式在实数范围内有意义？ （1）2-x （2）32-x （3）0)2(+x【课堂探究案】探究一：变量与函数问题1.一辆汽车以60千米/小时的速度匀速行驶，行驶里程为s 千米.行驶时间为t 小时.t/时1 2 3 4 5s/千米（1）填表：（2）在这个变化过程中，变化的量是_____，不变的量是_____。
变量____的值随变量____的值变化而变化。
问题2.票房收入问题：每张电影票的售价为10元，一场售出x 张电影票，票房收入为 y 元。
（1）若一场售出150张电影票，则该场票房收入是______，若一场售出205张，则该场票房收入是______； （2）在这个变化过程中，变化的量是_____，不变的量是_____。
变量____的值随变量____的值变化而变化。
问题3.在一根弹簧的下端悬挂重物，如果弹簧原长10cm ，每1kg 重物使弹簧伸长0.5cm ，设重物质量为xkg,受力后的弹簧长度为Lcm 。
物体的重量m(kg) 0 1 2 3 4 5 ... 弹簧的长度L(cm)（1）填表：（2）在这个变化过程中，变化的量是_____，不变的量是_____。
变量____的值随变量____的值变化而变化。
问题4.你见过水中涟漪吗? 在圆形水波慢慢的扩大过程中,圆的半径为r ，圆的面积S 。
半径r(cm)10 20 30圆的面积s(cm 2)（1）填表：（2）在这个变化过程中，变化的量是_____，不变的量是_____。
人教版八年级下册数学19.1.1 第1课时 常量与变量导学案
第十九章 函数青海一中 李清19.1 函数19.1.1 变量与函数 第1课时 常量与变量学习目标：1.了解常量与变量的概念，掌握常量与变量之间的联系与区别.2.学会用含一个变量的代数式表示另一个变量.重点：能够区分同一个问题中的常量与变量. 难点：用式子表示变量间的关系.一、知识链接1.人们在认识和描述某一事物时，经常会用“量”来具体表达事物的某些特征（属性），如：速度、时间、路程、温度、面积等，请你再写出三个“量”： 、 、 .同时用“数”来表明“量”的大小.2.写出路程（s ）、速度（v ）、时间（t ）之间的关系： . 二、新知预习1.小明去文具店购买一些铅笔，已知铅笔的单价为0．2元／支，总价y 元随铅笔支数x 的变化而变化，在这个问题中，变量是________，常量是________.2.圆的面积S 随着半径r 的变化而变化，已知它们的关系为:2r S π=,在这个问题中，常量是 ，变量是 .3.自主归纳：变量：在一个变化过程中，数值________的量为变量. 常量：在一个变化过程中，数值________的量为常量. 三、自学自测1.指出下列关系式中的常量和变量.（1）长方形的长为2，长方形面积S 与宽x 之间的关系S=2x ；（2）一批香蕉每千克6元，则总金额y （元）与销售量x （千克）之间的关系式为y=6x.2.一名运动员以8米/秒的速度奔跑，写出他奔跑的路程s （米）与时间t （秒）之间的关系式，并指出其中的变量和常量.____________________________________________________________ ____________________________________________________________探究点1：常量与变量问题1：一辆汽车以60千米／时的速度匀速行驶，行驶里程为s 千米．行驶时间为t 小时．（1）请同学们根据题意填写下表：（2）试用含t 的式子表示s,则s= ；（3）在以上这个过程中，变化的量有 ，不变化的量有__________． 问题2：每张电影票的售价为10元，如果早场售出票150张，日场售出205张，晚场售出31张，三场电影的票房收入各多少元？设一场电影售票x 张，t/小时 1 2 3 4 5 S/千米课堂探究教学备注配套PPT 讲授1.情景引入 （见幻灯片3）2.探究点1新知讲授（见幻灯片7-16）票房收入y元．（1）请同学们根据题意填写：早场电影的票房收入为元；日场电影的票房收入为元；晚场电影的票房收入为元；（2）在以上这个过程中，变化的量是_____________，不变化的量是__________．（3）试用含x的式子表示y,则y= ；这个问题反映了票房收入____随售票张数_____的变化过程．问题3：你见过水中涟漪吗?如图所示,形水波慢慢的扩大.在这一过程中,当圆的半径r分别为10cm,20cm,30cm时,圆的面积S分别为多少?（1）填空：当圆的半径为10cm时，圆的面积为 cm2；当圆的半径为20cm时，圆的面积为 cm2；当圆的半径为30c时，圆的面积为 cm2；当圆的半径为r时，圆的面积S= ；（2）在以上这个过程中，变化的量是_____________，不变化的量是__________．要点归纳：在一个变化过程中，数值发生变化的量为，数值始终不变的量为 .例1 指出下列事件过程中的常量与变量(1)某水果店橘子的单价为5／千克，买a千橘子的总价为m元，其中常量是________，变量是________；(2)周长C与圆的半径r之间的关系式是C＝r2π，其中常量是________，变量是________；(3)三角形的一边长5cm，它的面积S(cm2)与这边上的高h(cm)的关系式52 y h =中，其中常量是________，变量是________. 变式题阅读并完成下面一段叙述：（1）某人持续以a 米／分的速度用t 分钟时间跑了s 米，其中常量是________,变量是________.（2）s 米的路程不同的人以不同的速度a 米／分各需跑的时间为t 分，其中常量是________,变量是________.（3）根据上面的叙述，写出一句关于常量与变量的结论：_________________________.方法总结:区分常量与变量，就是看在某个变化过程中，该量的值是否可以改变，即是否可以取不同的值.探究点2：确定两个变量之间的关系例2.弹簧的长度与所挂重物有关．如果弹簧原长为10cm ，每1kg 重物使弹簧伸长0.5cm ，试填下表： 怎样用含重物质量m （kg ）的式子表示受力后的弹簧长度 L(cm)?变式题：如果弹簧原长为12cm ，每1kg 重物使弹簧压缩0.5cm ，则用含重物质量m （kg ）的式子表示受力后的弹簧长度 L(cm)为________. . 写出下列问题中的关系式，并指出变量和常量：（1）某市的自来水价为4元/吨.现要抽取若干户居民调查水费支出情况，记某户月用水量为x 吨，月应交水费为y 元.（2）某地手机通话费为0.2元/分.李明在手机话费卡中存入30元，记此后他的手机通话时间为t 分钟，话费卡中的余额为w 元.（3）水中涟漪（圆形水波）不断扩大，记它的半径为r ，圆周长为C ，圆周率（圆周长与直径的比）为π.（4）把10本书随意放入两个抽屉（每个抽屉内都放），第一个抽屉放入x 本，第二个抽屉放入y 本.二、课堂小结 常量与变量的概念常量 在一个变化过程中，数值________的量为变量变量在一个变化过程中，数值________的量为变量 易错提醒 在不同的条件下，常量与变量是相对的1.若球体体积为V ，半径为R ，则343V R π=，其中变量是________、________，常量是________.2.计划购买50元的乒乓球，所能购买的总数n(个)与单价 a （元）的关系式是________，其中变量是________，常量是________.3.汽车开始行使时油箱内有油40升，如果每小时耗油5升，则油箱内余油量Q （升）与行使时间t （小时）的关系是________，其中的常量是________，变量是________.4.表格列出了一项实验的统计数据，表示小球从高度x （单位：m ）落下时弹跳高度y （单位：m ）与下落高的关系，据表可以写出的一个关系式是 ．50 80 100 15025405075当堂检测教学备注 配套PPT 讲授5.当堂检测 （见幻灯片19-21）5.瓶子或罐头盒等物体常如下图那样堆放，试确定瓶子总数y 与层数x 之间的关系式.完成上表，并写出瓶子总数y 与层数x 之间的关系式.1、不求与人相比，但求超越自己，要哭旧哭出激动的泪水，要笑旧笑出成长的性格。
人教版数学八年级下册19.1.1《变量与函数》教学设计
-利用生活实例或数学问题，激发学生的好奇心，引导他们观察变量之间的变化规律。
-设计系列问题，逐步引导学生深入探讨函数的定义和性质。
2.运用合作学习、讨论交流的方法，提高学生的思维品质和解决问题的能力。
-组织学生进行小组合作，鼓励他们发表自己的观点，倾听他人的意见，共同解决问题。
-在下次课堂上，每个小组分享自己的解题过程和心得体会，促进同学之间的交流和学习。
5.思考与拓展：
-思考函数在生活中的应用，如天气预报、股票市场分析等，并简述函数在这些领域中的作用。
-探索函数的其他性质，如周期性、对称性等，并尝试举出相应的实际例子。
接着，我会引导学生思考：“如果我们想要预测未来某个时间点的气温，该怎么做呢？”从而引出变量和函数的概念。学生会发现，通过观察已经收集到的数据，可以尝试寻找气温与时间之间的关系，进而预测未来气温。这样，学生便对函数的概念有了初步的认识，为接下来的学习打下基础。
（二）讲授新知
在讲授新知环节，我会从以下几个方面展开：
-对于基础薄弱的学生，通过个别辅导和小组互助，帮助他们克服学习难点。
3.探究式学习，培养学生的思维能力
-采用问题驱动的教学方法，引导学生通过观察、实验、推理等过程，自主探究函数的定义和性质。
-设计开放性问题，鼓励学生多角度思考，培养他们的创新意识和解决问题的能力。
4.信息技术辅助，提高教学效果
-利用数学软件和多媒体工具，直观演示函数图象和变化过程，帮助学生形象地理解函数概念。
-通过网络资源，拓展学生的学习视野，使他们能够接触到更多与函数相关的实际应用。
5.实践活动，增强学生的应用能力
-安排课后实践活动，让学生在实际操作中运用函数知识，解决现实问题。
八年级数学下册 19.1.1 变量与函数学案 (新版)新人教版
19．1 函数19．1.1 变量与函数01 课前预习要点感知1 在一个变化过程中，数值发生变化的量叫做变量，数值始终不变的量叫做常量． 预习练习1－1 直角三角形两锐角的度数分别为x 、y ，其关系式为y ＝90－x ，其中变量为x ，y ，常量为90．要点感知2 在一个变化过程中，如果有两个变量x 与y ，并且对于x 的每一个确定的值，y 都有唯一确定的值与其对应，那么我们就说x 是自变量，y 是x 的函数．如果当x ＝a 时，y ＝b ，那么b 叫做当自变量的值为a 时的函数值．预习练习2－1 若球的体积为V ，半径为R ，则V ＝43πR 3.其中自变量是R ，V 是R 的函数． 要点感知3 函数自变量的取值范围既要满足函数关系式有意义，又要满足实际问题有意义． 预习练习3－1 甲乙两地相距100 km ，一辆汽车以每小时40 km 的速度从甲地开往乙地，t 小时与乙地相距s km ，s 与t 的函数解析式是s ＝100－40t ；自变量t 的取值范围是0≤t≤2.5. 02 当堂训练知识点1 变量与常量1．圆周长公式C ＝2πR 中，下列说法正确的是(D )A ．π、R 是变量，2为常量B ．R 是变量，2、π、C 为常量C ．C 是变量，2、π、R 为常量D ．C 、R 是变量，2、π为常量2．写出下列各问题中的数量关系，并指出各个关系式中，哪些是常量？哪些是变量？(1)购买单价为5元的钢笔n 支，共花去y 元；(2)全班50名同学，有a 名男同学，b 名女同学；(3)汽车以60 km /h 的速度行驶了t h ，所走过的路程为s km .解：(1)y ＝5n ，y 、n 是变量，5是常量．(2)a ＋b ＝50，a 、b 是变量，50是常量．(3)s ＝60t ，s 、t 是变量，60是常量．知识点2 函数的有关概念3．下列关系式中，一定能称y 是x 的函数的是(B )A ．2x ＝y 2B ．y ＝3x －1C .||y ＝23xD ．y 2＝3x －54．若93号汽油售价7.85元/升，则付款金额y(元)与购买数量x(升)之间的函数关系式为y ＝7.85x ，其中x 是自变量，y 是x 的函数．5．当x ＝2和x ＝－3时，分别求下列函数的函数值．(1)y ＝(x ＋1)(x －2)；(2)y ＝2x 2－3x ＋2.解：(1)当x ＝2时，y ＝(x ＋1)(x －2)＝(2＋1)×(2－2)＝0；当x ＝－3时，y ＝(x ＋1)(x －2)＝(－3＋1)×(－3－2)＝10.(2)当x ＝2时，y ＝2x 2－3x ＋2＝2×22－3×2＋2＝4；当x ＝－3时，y ＝2x 2－3x ＋2＝2×(－3)2－3×(－3)＋2＝29.知识点3 函数的解析式及自变量的取值范围6．(云南中考)函数y ＝1x －2的自变量x 的取值范围为(D ) A ．x ＞2 B ．x ＜2C ．x ≤2D ．x ≠27．正方形的边长为a ，面积为S ，若a 是自变量，则S 与a 之间的函数解析式可表示为(D )A ．S ＝a 4B ．S ＝4aC ．a ＝S 2D ．S ＝a 28．(眉山中考)在函数y ＝x ＋1中，自变量x 的取值范围是全体实数．9．(曲靖中考)如果整数x ＞－3，那么使函数y ＝π－2x 有意义的x 的值是1(只需填一个)．10．某商店进了一批货，每件进价为4元，售价为每件6元，如果售出x 件，售出x 件的总利润为y 元，那么y 与x 的函数关系式为y ＝2x.03 课后作业11．在△ABC 中，它的底边是a ，底边上的高是h ，则三角形面积S ＝12ah ，当a 为定长时，在此函数关系式中(A )A ．S ，h 是变量，12，a 是常量B ．S ，h ，a 是变量，12是常量C ．a ，h 是变量，12，S 是常量D ．S 是变量，12，a ，h 是常量12．(百色中考)已知函数y ＝⎩⎪⎨⎪⎧2x ＋1（x≥0），4x （x<0），当x ＝2时，函数值y 为(A ) A ．5 B ．6 C ．7 D ．813．(黔南中考)函数y ＝2x －2的自变量x 的取值范围在数轴上表示正确的是(B )14．若等腰三角形的周长为60 cm ，底边长为x cm ，一腰长为y cm ，则y 关于x 的函数解析式及自变量x 的取值范围是(D )A ．y ＝60－2x(0<x<60)B ．y ＝60－2x(0<x<30)C ．y ＝12(60－x)(0<x<60)D ．y ＝12(60－x)(0<x <30)15．圆的面积S ＝πr 2中，自变量r 的取值范围是r>0．16．(安顺中考)在函数1－x x ＋2中，自变量x 的取值范围是x ≤1且x≠－2. 17．已知水池中有800立方米的水，每小时抽50立方米．(1)写出剩余水的体积Q(立方米)与时间t(小时)之间的函数解析式；(2)写出自变量t 的取值范围；(3)10小时后，池中还有多少水？解：(1)剩余水的体积Q ＝800立方米－抽掉的水的体积，即Q ＝800－50t.(2)抽完水所需时间为：0＝800－50t，得t＝16，所以0＜t≤16.(3)当t＝10时，即Q＝800－50t＝800－50×10＝300(立方米)．18．圆柱的底面半径是2 cm，当圆柱的高h(cm)由大到小变化时，圆柱的体积V(cm3)随之发生变化．(1)在这个变化过程中，自变量和自变量的函数各是什么？(2)在这个变化过程中，写出圆柱的体积V与高h之间的关系式？(3)当h由5 cm变化到10 cm时，V是怎样变化的？(4)当h＝7 cm时，V的值等于多少？解：(1)自变量是圆柱的高，自变量的函数是圆柱的体积．(2)体积V与高h之间的关系式V＝π·22h＝4πh.(3)当h＝5 cm时，V＝20π (cm3)；当h＝10 cm时，V＝40π (cm3)．当h越来越大时，V也越来越大．(4)当h＝7 cm时，V＝4π×7＝28π (cm3)．挑战自我19．如图，长方形ABCD中，当点P在边AD(不包括A，D两点)上从A向D移动时，有些线段的长度和三角形的面积始终保持不变，而有些则发生了变化．(1)试分别写出长度变和不变的线段，面积变和不变的三角形；(2)假设长方形的长AD为10 cm，宽AB为4 cm，线段AP的长为x cm，分别写出你所列出的变化的线段PD的长度(y)、△PCD的面积(S)与x之间的函数解析式，并指出自变量的取值范围．解：(1)长度变化的线段有：AP，PD，BP，PC；面积变化的三角形有：△APB，△DCP ； 长度不变的线段有：AB ，BC ，CD ，AD ；面积不变的三角形有：△BPC.(2)根据题意可知：PD ＝AD －AP ，AD ＝10 cm ，AP ＝x cm ， ∴y ＝10－x ，其中0＜x ＜10.根据题意可知：△PCD 的面积为12·DC·PD，∴S ＝12×4×(10－x)＝20－2x.其中0＜x ＜10.。
八年级数学下册 第19章 一次函数 19.1 变量与函数 19.1.1 变量与函数教案
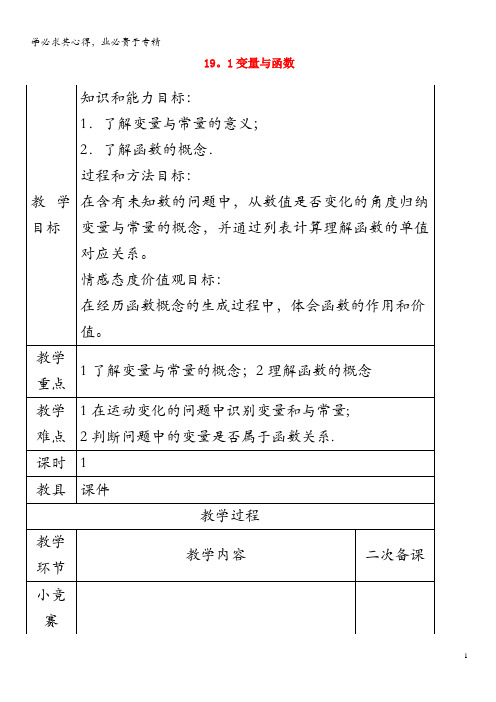
售出票数x
100
120
140
160
180
……
票房收入y
①找一名学生填表，让学生一起分析y与x是不是单值对应关系;
②描述y与x的单值对应关系.
【设计意图】通过模仿训练，尝试初步理解单值对应的含义.
3、圆形水波慢慢地扩大，在这一过程中,圆的半径r 厘米 ,圆的面积为S 平方厘米，圆周率（圆周长与直径之比)为π.
（4）思考问题4中，矩形的宽y为自变量，矩形的长x是y的函数是否正确
①强调辨别函数的关键是：是否有两个变量，并且变量是否是单值对应关系；
②补充说明：一般地，主动变化的量是自变量,随之变化的量是函数。
【设计意图】借此例，将自变量与函数互换，说明只要满足单值对应,就可以用函数来表示这种关系，灵活理解函数的定义。
【设计意图】通过这三道例题，使学生学会根据定义判断函数关系，经过反复训练，突破难点.
4、P是数轴上的一个动点,它到原点的距离记为 x，它的坐标记为 y，y 是 x 的函数吗？为什么？
【设计意图】通过这道题,说明点的坐标y与绝对值x不是单值对应关系，所以不是函数；但反过来，x却是y的函数，采用小组讨论的方式，升华对函数定义的理解.
练习1:指出下列变化过程中的变量和常量:
1、某市的自来水价为4元/吨,现要抽取若干户居民调查水费支出情况，记某户月用水量为 x 吨,月应交水费为 y 元；
2、某地手机通话费为0.2元/分，李明在手机话费卡中存入30元，记此后他的手机通话时间为t 分，话费卡中的余额为w 元;
3、水中涟漪（圆形水波）不断扩大，记它的半径为r，圆周长为C，圆周率（圆周长与直径之比）为π；
人教版数学八年级下册19.1《变量与函数(1)》导学案2
19.1.1 变量与函数〔1〕【学习目标】知识与技能：理解变量、常量的概念以及相互之间的关系；能指出一个变化过程中的变量与常量。
过程与方法：能找出变量之间的简单关系，列出简单关系式。
情感态度与价值观：学生通过对实际问题的讨论和分析，感受事物变化过程的普遍性，体会事物之间的相互联系与制约。
【学习重点】1．认识变量、常量．2．变量、常量必须存在于一个变化过程中【学习难点】常量与变量之间的关系，准确判断变量。
【课时安排】：1课时一、新课导入问题一：我到超市购置了假设干瓶矿泉水，这种矿泉水的单价是每瓶1.2元，花费的总金额为y元，购置的瓶数为x瓶，先填写下表，再用含x的式子表示y.1．请同学们根据题意填写下表：2．在以上这个过程中，变化的量是_____________．不变化的量是__________．3．试用含x的式子表示y. y=_________________．这个问题反映了购置矿泉水需要的钱____随购置的数量___的变化过程．问题二：一辆汽车以60千米／小时的速度匀速行驶，行驶里程为s千米，行驶时间为t小时．1.请同学们根据题意填写下表：请说明你的道理：路程=__________________2.．在以上这个过程中，变化的量是_____________．不变化的量是__________．3．试用含t 的式子表示s ．s=_________________这个问题反映了匀速行驶的汽车所行驶的路程___随行驶时间___的变化过程． 二、预习导学【活动一】以上这些问题都反映了不同事物的变化过程，其实现实生活中还有好多类似的问题，在这些变化过程中，有些量的值是按照某种规律变化的〔如______________〕，有些量的数值是始终不变的〔如______________ 〕 结论： 在一个变化过程中，我们称数值发生变化．．．．的量为________； 在一个变化过程中，我们称数值始终不变．．．．的量为________； 【活动二】例题讲解指出以下关系式中的变量与常量：(1) y = 5x －6 (2) y=(3) y= 4x 2＋5x －7 (4) S = Лr 2解：〔1〕5和-6是常量，x 和y 是变量。
人教版八年级下第19章一次函数19.1.1变量与函数教案
3.培养学生合作交流、自主探究的学习习惯，提高数学建模和数学运算的核心素养。
4.激发学生学习兴趣，培养勇于挑战、善于思考的学习态度，提升学生的数学素养和综合素质。
在教学过程中，重点关注学生在以下方面的表现：
1.能否运用所学知识，分析并解决实际问题，体现数学的应用价值。
3.重点难点解析：在讲授过程中，我会特别强调变量与常量的区别以及函数的三要素。对于难点部分，我会通过举例和图示来帮助大家理解一次函数的定义和图像特点。
（三）实践活动（用时10ቤተ መጻሕፍቲ ባይዱ钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与一次函数相关的实际问题，如公交车票价与乘车距离的关系。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作，比如用尺子和直尺绘制一次函数的图像，观察斜率和截距的变化。
五、教学反思
在上完这节课之后，我对自己的一些教学设计和学生的反应进行了思考。我发现，通过生活中的实例引入变量和函数的概念，学生们能够更直观地理解这些抽象的数学概念。他们对于一次函数的应用表现出浓厚的兴趣，尤其是当我将函数与他们的日常生活联系起来时，比如购物打折、手机话费等问题。
我注意到，在教学过程中，有些学生对一次函数的图像绘制感到困惑。我意识到，这里可能需要更多的直观演示和实际操作，让学生亲手尝试，从而更好地理解图像的生成过程。在接下来的课程中，我打算增加一些互动环节，比如让学生分组在教室里用道具来模拟一次函数的图像，这样既能增强他们的动手能力，也能加深对一次函数图像特征的理解。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解变量与函数的基本概念。变量是随着某些条件变化而变化的量，而函数则是描述两个变量之间依赖关系的数学模型。它们在数学和生活中都有着广泛的应用。
19.1.1变量与函数导学案(人教版)
19.1.1《变量与函数》导学案班级_________ 姓名__________学习目标：1.结合实例，了解常量、变量的意义和函数的概念；2.能确定简单实际问题的函数解析式，并会求函数值。
引言：大千世界处在不停的运动变化中，万物皆变。
静止是相对的，运动是永恒的。
在运动变化过程中往往蕴含着量的变化。
那么，数学上怎样刻画各种运动变化呢？情境探究:.（1）4时的气温是多少？10时，16时呢？当时间t的值确定后，能确定气温T的值吗？当时间t取定一个值时，气温T就有唯一确定的值与其对应.（2）气温T的值随什么的值的变化而变化呢？60 km/h的速度匀速行驶，行驶的路程为s km，行驶时间为t h．请回答问题：（1）填表：它们之间的关系用式子如何表示?（2）数值变化的量是，数值始终不变的量是。
当时间t的值确定后，能确定路程s的值吗？当时间t取定一个值时，路程s就有______________________与其对应.（3）s的值随什么的值的变化而变化呢？情境3：圆形水波慢慢地扩大。
圆的面积为S cm2 ，圆的半径为r cm.请思考并回答问题：（1）当圆的半径r分别为10cm,20cm,30cm时，圆的面积S分别为多少？它们之间的关系用式子如何表示?（2）数值变化的量是，数值始终不变的量是。
当半径r的值确定后，能确定圆面积S的值吗？当半径r取定一个值时，面积S就有_____________________与其对应.（3）S的值随什么的值的变化而变化呢？情境4：福利院院长告诉同学们，福利院准备在院里修建一个周长为40m的矩形水池喂养金鱼.，如果矩形的一边长为x m，它的邻边长为y m．请思考如下问题：（1）当矩形的一边长x分别为5m,8m,12m时，它的邻边长为y分别为多少？它们之间的关系用式子如何表示?（2）数值变化的量是，数值始终不变的量是。
当一边x的值确定后，能确定邻边y的值吗？能确定几个邻边的值?当x取定一个值时，邻边y就有______________________与其对应.（3）y的值随什么的值的变化而变化呢？情境5：李强回到家完成了数学作业，内容涉及：（1）完成下列表格：数x 1 2 3 4 5平方根y当数x的值确定后，能确定平方根y的值吗？当数x取定一个值时，平方根y就有____________与其对应.（3）下图反映的是蚂蚁在墙上爬行的高度h与离出发点水平距离s关系图.当s的值确定后，能确定h的值吗？当s取定一个值时，h就有____________与其对应.生活中，一个量随另一个量的变化而变化的现象大量存在.在变化过程中涉及的量,有些量的数值是变化的,有些量的数值是始终不变的.在一个变化过程中，我们称数值发生变化的量为变量，数值始终不变的量为常量.我们再回顾刚才探究的5个情境，请同学们小组群学，完成表格并思考问题，最后请同学展示交流。
19.1.1变量与函数导学案
19.1.1 变量与函数（1）学校：_________班级：__________姓名：___________第______组第______号★学习目标：1、能分清实例中的常量和变量、自变量与函数，理解函数的定义。
2、理解掌握确定函数关系式。
一、课前预学与疑难交流（阅读教材70页~74页）1、P71汽车以60km/h的速度匀速行驶，行驶路程为y km，行驶时间为x h，yP71在一个变化过程中：发生变化的量叫做_________；不变的量叫做_________。
在上述汽车行驶的过程中，y的值随x的值的变化________，变量是_______，常量是____， y与x的关系式是_________ 。
因为数是固定不变的，所以在一个关系式中，常量是数，而字母可以取相应变化的值，所以变量是字母。
下列运动变化过程中的关系式，哪些是变量，哪些是常量：①y=0.4x 常量：变量：②a=3+2.4b 常量：变量：③C=2πR 常量：变量：④V=6abc 常量：变量：2、函数的相关概念：P73一般地，在一个变化过程中，如果有____个变量___与___，并且对于____的每一个确定的值，____都有___________的值与其对应，那么我们就说 x是_________，y是 x的______．如果当x=a 时，对应的y=b，那么 b 叫做当自变量的值为a时的_______.P74用关于自变量的数学式子表示函数与自变量之间的关系，这种式子叫做函数的_________．在上述汽车行驶的过程中， y与x的关系式是_________，这其中有____个变量，给一个x,得____个y，所以____是自变量，_____是_____的函数。
x=1时，y的函数值是60；x=2时，y的函数值是120；x=3时，y的函数值是_______；x=4时，y的函数值是_______。
函数解析式即y与x的关系式：___________.y是x的函数吗？如果是，指出自变量。
人教版数学八年级下册19.1.1《变量与函数》教学设计
人教版数学八年级下册19.1.1《变量与函数》教学设计一. 教材分析《变量与函数》是初中数学的重要内容，人教版八年级下册19.1.1节主要介绍了变量的概念以及函数的定义。
通过本节课的学习，学生能够理解变量、常量的概念，了解函数的定义及表示方法，为后续学习函数的性质、图象等知识打下基础。
二. 学情分析学生在学习本节课之前，已经掌握了代数基础知识，如代数式、方程等。
但他们对变量的概念及函数的定义还较为模糊，需要通过实例和练习来进一步理解和掌握。
此外，学生可能对函数的表示方法感到陌生，需要通过教师的引导和学生的实践来逐步熟悉。
三. 教学目标1.知识与技能：使学生理解变量、常量的概念，掌握函数的定义及表示方法。
2.过程与方法：通过实例分析，让学生体会变量之间的依赖关系，学会用函数表示实际问题中的变量关系。
3.情感态度与价值观：培养学生对数学的兴趣，提高学生运用数学知识解决实际问题的能力。
四. 教学重难点1.重点：变量、常量的概念，函数的定义及表示方法。
2.难点：函数概念的理解，函数表示方法的运用。
五. 教学方法1.情境教学法：通过生活实例引入变量、常量概念，让学生在具体情境中感受数学与生活的联系。
2.引导发现法：教师引导学生发现变量之间的依赖关系，自主探究函数的定义及表示方法。
3.实践操作法：让学生通过实际操作，加深对函数概念的理解，提高运用函数解决实际问题的能力。
六. 教学准备1.教学课件：制作涵盖实例、练习、拓展等环节的课件，以便于引导学生逐步深入学习。
2.教学素材：收集与生活相关的函数实例，如温度、身高、体重等，用于导入和巩固环节。
3.练习题库：准备不同难度的练习题，以便于针对性地进行操练和巩固。
七. 教学过程1.导入（5分钟）教师通过展示生活中常见的变量关系，如气温随时间的变化、身高与年龄的关系等，引导学生关注变量之间的依赖关系。
在此基础上，提出问题：“你们认为什么是变量？什么是常量？”让学生发表自己的见解。
人教版初二数学下册19.1变量与函数的导学案
19.1变量与函数第一课时导学案值？上面的三个问题中，有什么共同特点？(1) 有两个变量：①时间 t 、相应的高度 h ;②层数n 、物体 总数y ;③汽车速度v 、滑行距离s .(2) 如果给定其中一个变量 (自变量)的值，相应地就确定了另 一个变量(因变量)的值(唯一的).(3) 为了符合实际，两个变量都有相应的变化范围.1.函数的概念：一般地，在某个变化过程中，有两个变量 x和y ,如果给定一个 x 值，相应地就确定了一个 y 值，那么我 们称y是x 的函数(function),其中x 是自变量，y 是因变量.2•函数三种表达方式：(1) 用数学式子表示函数的方法叫做解析法. (2) 用图象来表示函数的方法是图象法.(3) 把自变量x 的一系列值和函数 y 的对应值列成一个表来 表示函数的方法叫做列表法.3 .理解函数的概念应抓住以下两点：(1) 函数不是某个具体数，它是指某一变化过程中两个变量 之间的关系.(2) 判断两个变量是否有函数关系不是看它们之间是否有关 系式存在，更重要地看对于 x 的每一个确定的值， y 是否有唯一确定的值和它对应.考考你•判断：下列各变量之间的关系，能不能构成函数关系？(1). 圆的周长与半径；( )⑵. 正方形的面积与边长； ( ) ⑶. 长方形的面积与长方形的长；( ) ⑷.关系式y= x 中，y 是x 的函数；() 问题三、瓶子或罐头盒等圆柱形的物体，常常如下图那样堆 探索 新知 放。
随着层数的增加，物体的总数是如何变化的?层数 n12345物体总数 y• •其中对于给定的每一个层数 n ，物体总数 y 对应有几个现不同的特 点给予肯定， 能发现越多 越好，给学生 一个充分自 由思考的空 间教师提问， 学生独立思考 再合作交流得 岀函数定义老师解释函数 的定义并强调 函数概念应注 意的地方，然后 介绍函数的表 示方法。
学生理解记忆⑸.关系式y = ±x中,y是x的函数。
八年级数学下册 19.1.1 变量与函数导学案 (新版)新人
一次函数19.1 函数19.1.1 变量与函数1.认识变量、常量.2.学会用一个变量的代数式表示另一个变量.3.认识变量中的自变量与函数.4.进一步理解掌握确定函数关系式.5.会确定自变量的取值范围.自学指导：阅读教材第71页至74页，独立完成下列问题：知识探究(1)一辆汽车以60千米/时的速度匀速行驶，行驶里程为s千米，行驶时间为t小时.①根据题意填写下表：t/时 1 2 3 4 5s/千米60 120 180 240 300②试用含t的式子表示s为s=60t；③在以上这个过程中，不变化的量是60，变化的量是s与t.(2)每张电影票的售价为10元，早场售出票150张，日场售出票205张，晚场售出票310张.①三场电影的票房收入分别是1500元，2050元，3100元.②设一场电影售票x张，票房收入y元，则用含x的式子表示y为y=10x.③在以上这个过程中，不变化的量是10，变化的量是x与y.(3)变量：在一个变化的过程中，数值变化的量；常量：在一个变化的过程中，数值不变的量.(4)一般地，在一个变化过程中，如果有两个变量x与y，并且对于x的每一个变化值，y都有唯一确定的值与其对应，那么就称y是x的函数，其中x是自变量，如果当x=a时，y=b，那么b叫做当自变量的值为a时的函数. (5)对于一个已知的函数，自变量的取值范围是使这个函数有意义的一切值；对于一个实际问题，自变量的取值必须使实际问题有意义.活动1 学生独立完成例1 分别指出下列关系中的变量和常量：(1)圆面积公式S=πr2(s表示面积，r表示半径)；(2)匀速运动公式s=vt(v表示速度，t表示时间，s表示在时间t内所走的路程).解：(1)r、S是变量，π是常量；(2)t、s是变量，v是常量.π是圆周率，是定值，是常量，半径r每取一个值都有唯一的S值和它对应，故S和r是变量.因为是匀速运动，所以速度v是常量，t和s是变量.例2 如图，一个矩形推拉窗高1.5m，则活动窗的通风面积S(m2)与拉开长度b(m)的关系式是S=1.5b.窗高1.5m是一边长，拉开长度b(m)是另一边长，因此通风面积S=1.5b.例3 某火力发电厂，贮存煤1000吨，每天发电用煤50吨，设发电天数为x，该电厂开始发电后，贮存煤量为y(吨).(1)写出y与x之间的函数关系式；(2)为了保障电厂正常发电，工厂每天将从外地运回煤45吨，请写出按此方案执行时，y与x之间的函数关系式，并求出发电30天时，电厂贮存煤多少吨？解：(1)y=-50x+1000；(2)y=-5x+1000，当x=30时，y=-5×30+1000=850.∴当发电30天时，电厂贮存煤850吨.电厂贮存的煤量与原贮存量，每天发电的用煤量，每天从外地运回的煤量，以及发电天数有关.活动2 跟踪训练1.设圆柱的高h不变，圆柱的体积V与圆柱的底面半径r的关系是V=πr2h，这个式子中常量是π，h，变量是V，r.2.若球体体积为Ｖ，半径为Ｒ，则Ｖ＝43πＲ3.其中变量是R，V，常量是43，π.找准不变的量，再确定变量.3.下列变量间的关系：①人的身高与年龄；②矩形的周长与面积；③圆的周长与面积；④商品的单价一定，其销售额与销售量，其中是函数关系的有③④.一是明确已知两个变量是什么；二是看两个变量之间是否存在一一对应关系.4.某市为了鼓励居民节约用水，对自来水用户按如下标准收费：若每月每户用水不超过12米3，按每立方米a元收费；若超过12米3，则超过部分每立方米按2a元收费，某户居民五月份交水费y(元)与用水量x(米3)(x>12)之间的关系式为y=2ax-12a，若该月交水费20a元，则这个月实际用水16米3.5.若等腰三角形底角度数值为x，则顶角度数值y与x的关系式是y=-2x＋180，变量是x，y，常量是-2，180.6.在△ABC中，它的底边长是a，底边上的高是h，则三角形的面积S=12ah，当底边a的长一定时，在关系式中的常量是12，a，变量是S，h.7.已知水池里有水200m3，每小时向水池里注水20m3，设注水时间为x小时，水池里共有水ym3，用含x的式子表示y，则y=20x+200，其中变量为x，y，常量为20，200.8.人的心跳速度通常与人的年龄有关，如果a表示一个人的年龄，b表示正常情况下每分钟心跳的最高次数，经过大量试验，有如下的关系：b=0.8(220-a).(1)上述关系中的常量与变量各是什么？(2)正常情况下，一名15岁的学生每分钟心跳的最高次数是多少？解：(1)常量0.8，220，变量a,b； (2)164.9.蓄水池中原有水800m3，每小时从中放出60m3的水.(1)写出池中的剩余水量Q(m3)与放水时间t(h)之间的函数关系式；(2)写出自变量t的取值范围；(3)12h后，池中还有多少水？解：(1)Q＝-60t＋800； (2)0≤t≤403； (3)80m3.实际问题中的函数关系，自变量除了要使函数关系式本身有意义，还要满足实际意义.此题要根据函数Q的取值范围0≤Q≤800来确定自变量t的取值范围.活动3 课堂小结1.常量和变量是普遍存在的，它们只是相对于某个变化过程而言的两个概念，因此对它们的差别应紧扣定义及相应的实际背景.2.判断变量之间是否存在函数关系，主要抓住两点：一个变量的数值随着另一个变量的数值的变化而变化；自变量的每一个确定的值，函数都有且只有一个值与之对应.3.确定自变量取值范围时，不仅要考虑函数关系式有意义，而且还要注意使实际问题有意义.教学至此，敬请使用学案当堂训练部分.。
19.1.1 函数
第19章一次函数第1课时 19.1.1 变量与函数导学案（1）【学习目标】1．了解变量与常量的意义；2．体会运动变化过程中的数量变化．3. 从典型实例中抽象概括出函数的概念，了解函数的概念．【学习重点】了解变量与常量的意义，充分体会运动变化过程中量的变化．概括并理解函数概念中的单值对应关系．【学习难点】从典型实例中抽象概括出函数的概念一、学前准备1、预习：阅读书P70-71二、探索思考探究（一）1、下面问题中变化的量和不变的量：（1）汽车以60 km/h 的速度匀速行驶，行驶时间为t h，行驶路程为s km．变化的量：；不变的量：（2）每张电影票的售价为10 元，设某场电影售出x张票，票房收入为y元．变化的量：；不变的量：（3）圆形水波慢慢地扩大，在这一过程中，当圆的半径r 分别为10 cm，20 cm，30 cm 时，圆的面积S 分别为多少？在这个过程中，哪些量是变化的？S=10 时，r= cm；S=20 时，r= cm；S=30 时，r= cm变化的量：；不变的量：（4）用10 m长的绳子围一个矩形，当矩形的一边长x 分别为3 m，3.5 m，4 m，4.5 m 时，它的邻边长y 分别为多少？在矩形改变形状的变化过程中，哪些量是变化的？哪些量是固定不变的？x=3 时，y= cm；x=3.5 时，y= cm；x=4 时，y= cm；x=4.5 时，y= cm变化的量：；不变的量：数值发生变化的量为；数值始终不变的量为练习一、指出下列变化过程中的变量和常量：（1）汽油的价格是7.4元/升，加油x L，车主加油付油费y 元；变量；常量（2）小明看一本200 页的小说，看完这本小说需要t 天，平均每天所看的页数为n；变量；常量（3）用长为40 cm 的绳子围矩形，围成的矩形一边长为x cm，其面积为S cm2．变量；常量探索（二）1、探索（一）个问题中各有几个变量？2、每个问题中的变量之间有什么联系？归纳：1、每个变化的过程中都存在着（）变量.2、2两个变量互相联系，当其中一个变量确定一个值时，另一个变量就（）。
变量与函数--教学设计(李新卫)
课题：19.1.1 变量与函数（第1课时）教学设计李新卫（湖北省武汉市经济技术开发区第四中学）一、内容和内容解析1. 内容人教版《义务教育课程标准实验教科书数学》八年级下册：“19.1.1变量与函数”第1课时.2. 内容解析本节内容为《一次函数》第一课时. 在学生学习了二元一次方程和找规律的基础上，学生对变量和常量已有一些模糊的认识. 通过生活实例的感悟，由具体到抽象，抽象出量的意义，并对量进行分类得出变化的量和不变的量，归纳出变量与常量的概念. 同时在讨论问题过程中，引出变量间的单值对应关系，体会建模思想，为学习函数的定义、函数的表达方式、函数的取值范围及函数的应用做出铺垫，为《一次函数》全章的学习打下基础.根据以上的分析，本节课的教学重点确定为：通过列举生活实例，理解量的意义，逐步形成常量与变量的概念，并能指出实际问题中的常量与变量.二、目标和目标解析1. 目标（1）理解量的意义、常量与变量的概念，并能指出实际问题中的常量与变量；（2）在实际问题的探究过程中，感受生活中变量间的对应关系，学会分辨不同表达方式中的变量与常量，经历从具体到抽象、从感性认识到理性分析的思维过程，体会函数与方程、数形结合和分类讨论的数学思想，提升数学抽象和数学建模的核心素养.2. 目标解析本节内容从学生熟悉的实际问题出发，让学生体会变量间的单值对应关系，感受一个变量随另一个变量的变化而变化，渗透自变量与函数的关系，从具体到抽象，通过表格、关系式及图象让学会生认识运动过程中的变量和常量概念，进而认识相关概念的联系和区别.达成目标（1）的标志：在探究过程中，正确找到变量与常量，并找出变化规律；达成目标（2）的标志：在练习和拓展中，找到图表中隐藏的变量与常量，能读取不同的数量关系和表达方式.三、教学问题诊断分析学生在字母表示数中，接触过当字母取值变化时，代数式的值随之变化，但学生对量的意义较为模糊.学生在生活中具有对两个量之间关联的体验，如气温随时间变化等，学生对变量与常量的定义理解困难不大，但是对变化中的单值对应关系及在变化过程中寻找变量与常量较难把握，特别是函数中的“唯一确定”仅局限于通过公式求出的唯一值，对不能用公式求出值的单值对应关系难以理解.因此教学难点确定为：理解变化过程中的变量与常量，以及变量与常量的相对性.四、教学支持条件分析从学生学过的小学课文《秋天来了》，引导学生观察现实世界和日常生活中的变化现象，让学生会用“变”的眼光观察现实世界，会用数学思维思考现实世界，会用数学语言表达现实世界.以李强的活动情境为主线引出生活中的变化事例，发现生活中变化的量和不变的量，引出变量与常量，在事例中感悟一个量随另一个量的变化现象，为刻画变量间的依赖关系，形成函数概念做出铺垫.以大量生活问题题材引导学生发现生活中变化的量和不变的量，以及变量间的单值对应关系，引导学生分析、分类、归纳出变量与常量的概念，结合式子、表格和图形给学生多种变量对应关系的呈现方式，帮助学生使用变量与常量准确地表述数学的研究对象，学会用数学的语言表达和交流数学问题，积累抽象思维的经验，提升数学抽象素养。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
19.1.1变量与函数导学案（1）
学习目标：
1、通过探索具体问题中的数量关系和变化规律了解常量、变量的意义.
2、学会用含一个变量的代数式表示另一个变量.
学习重点：
教学重点：了解常量与变量的意义；
学习难点：较复杂问题中常量与变量的识别
学习过程:
活动一:情境创设，引出新知(5分钟)
根据题意填写下表,并回答问题
汽车以60千米／小时的速度匀速行驶，行驶里程为s千米，行驶时间为t小时．
1、在以上这个过程中，变化的量是_____________．不变化的量是__________．
2、试用含t的式子表示s=________,t的取值范围是这个问题反映了匀速行驶的汽车所行驶的路程____随行驶时间___的变化过程．
通过本节课的学习，相信大家一定能够解决这些问题．
活动二：观察分析，探究新知
问题二:每张电影票的售价为10元，如果早场售出票150张，午场售出205张，晚场售出310张，三场电影的票房收入各多少元？设一场电影售票x张，票房收入y元．•
1、在以上这个过程中，变化的量是_____________．不变化的量是__________．
2、试用含x的式子表示y，y=______ ,x的取值范围是 .
这个问题反映了票房收入_________随售票张数_________的变化过程．
问题三：当圆的半径r分别是10cm,20cm,30cm时，圆的面积S分别是多少？
1．在以上这个过程中，变化的量是_____________．不变化的量是__________．
2．试用含S的式子表示r，S=___ ,r的取值范围是 .这个问题反映了____随____的变化过程．
问题四：用10m长的绳子围成长方形，试改变长方形的长度，观察长方形的面积怎样变化．记录不同的矩形的长度值，计算相应的矩形面积的值，探索它们的变化规律。
设矩形的长为xm，面积为Ｓm2 .
1、在以上这个过程中，变化的量是_____________．不变化的量是__________．
2、试用含x的式子表示s． S=__________________,x的取值范围是 . 这个问题反映了矩形的___ _ 随_ __的变化过程．
师生小结：
在一个变化过程中，我们称数值发生变化
．．．．的量为________；在一个变化过程中，我
们称数值始终不变
．．．．的量为________；
活动三：师生互动，运用新知
1、一支圆珠笔的单价为2元，设圆珠笔的数量为x支，总价为y元。
则y= ；在这个式子中，变量是，常量是。
2、某种报纸的价格是每份0.4元，买x份报纸的总价为y元。
用含x的式子表示y，y＝，常量是，变量是。
3、一个三角形的底边长5cm，高h可以任意伸缩．写出面积Ｓ随h变化关系式，并指出其中常量与变量．
活动四：达标测评，深化新知
1．小军用50元钱去买单价是8元的笔记本，则他剩余的钱Q•（元）与他买这种笔记本的本数x之间的关系是（）
A．Q＝8x B．Q＝8x－50 C．Q＝50－8x D．Q＝8x＋50 2．甲、乙两地相距S千米，某人行完全程所用的时间t（时）与他的速度v（千米/
时）满足S=vt，在这个变化过程中，下列判断中错误的是（）
A．S是变量 B．t是变量 C．v是变量 D．S是常量
3．长方形相邻两边长分别为x、•y•，面积为100•，•则用含x•的式子表示y•，则y＝_______，在这个问题中，常量；是变量．
4．某种报纸的价格是每份0.4元,买x份报纸的总价为y元,先填写下表,再用含x的式子表示y．
x与y之间的关系是y＝ ,在这个变化过程中，常量是 ,变量是．
5.一盛满30吨水的水箱，每小时流出0.5吨水，试用流水时间t•（小时）表示水箱中的剩水量y（吨），y＝，t的取值范围是 . 活动五：课堂小结，巩固新知
1、你获得了哪些新知识，在哪些方面有进步
2、你还有哪些困惑的地方?
活动六：作业布置，加固新知
指出其中的变量和常量．
（1）用20cm的铁丝所围的长方形的长x（cm）与面积S（cm2）的关系．
（2）直角三角形中一个锐角α与另一个锐角β之间的关系．
（3）一盛满30吨水的水箱，每小时流出0.5吨水，试用流水时间t•（小时）表示水箱中的剩水量y（吨）．。