第六章 刚体转动自测题答案
大学物理第6章习题参考答案

第六章习题解答6-1 解:首先写出S 点的振动方程 若选向上为正方向,则有:0c o s02.001.0ϕ=- 21cos 0-=ϕ,0s i n 00>-=ϕωυA 0sin 0<ϕ 即 πϕ320-=或π34 初始相位 πϕ320-=则 m t y s )32cos(02.0πω-=再建立如图题6-1(a)所示坐标系,坐标原点选在S 点,沿x 轴正向取任一P 点,该点振动位相将落后于S 点,滞后时间为: ux t =∆则该波的波动方程为:m u x t y ⎥⎦⎤⎢⎣⎡--=πω32)(cos 02.0若坐标原点不选在S 点,如习题6-1图(b )所示,P 点仍选在S 点右方,则P 点振动落后于S 点的时间为: uL x t -=∆则该波的波方程为:m uL x t y ⎥⎦⎤⎢⎣⎡---=πω32)(cos 02.0若P 点选在S 点左侧,P 点比S 点超前时间为ux L -,如习题6-1图(c)所示,则⎥⎦⎤⎢⎣⎡--+=πω32)(cos 02.0u x L t y⎥⎦⎤⎢⎣⎡---=πω32)(cos 02.0uL x t∴不管P 点在S 点左边还是右边,波动方程为: ⎥⎦⎤⎢⎣⎡---=πω32)(cos 02.0uL x t y6-2 解(1)由习题6-2图可知, 波长 m 8.0=λ 振幅A=0.5m习题6-1图习题6-1图频率 Hz 125Hz 8.0100===λuv周期 s 10813-⨯==vT ππυω2502==(2)平面简谐波标准波动方程为: ⎥⎦⎤⎢⎣⎡+-=ϕω)(cos u xt A y 由图可知,当t=0,x=0时,y=A=0.5m ,故0=ϕ。
将ϕπωω、、、u v A )2(=代入波动方程,得:m )100(250cos 5.0⎥⎦⎤⎢⎣⎡-=x t y π(3) x =0.4m 处质点振动方程.⎥⎦⎤⎢⎣⎡-=)1004.0(250cos 5.0t y π m )250cos(5.0ππ-=t6-3 解(1)由习题6-3图可知,对于O 点,t=0时,y=0,故2πϕ±=再由该列波的传播方向可知,00<υ取 2πϕ=由习题6-3图可知,,40.0m OP ==λ且u=0.08m/s ,则ππλππω52rad/s 40.008.0222====u v rad/s可得O 点振动表达式为:m t y )252cos(04.00ππ+=(2) 已知该波沿x 轴正方向传播,u=0.08m/s,以及O 点振动表达式,波动方程为:m x t y ⎥⎦⎤⎢⎣⎡+-=2)08.0(52cos 04.0ππ(3) 将40.0==λx 代入上式,即为P 点振动方程:m t y y p ⎥⎦⎤⎢⎣⎡+==ππ2152cos 04.00 (4)习题6-3图中虚线为下一时刻波形,由图可知,a 点向下运动,b 点向上运动。
理论力学课后习题答案-第6章--刚体的平面运动分析
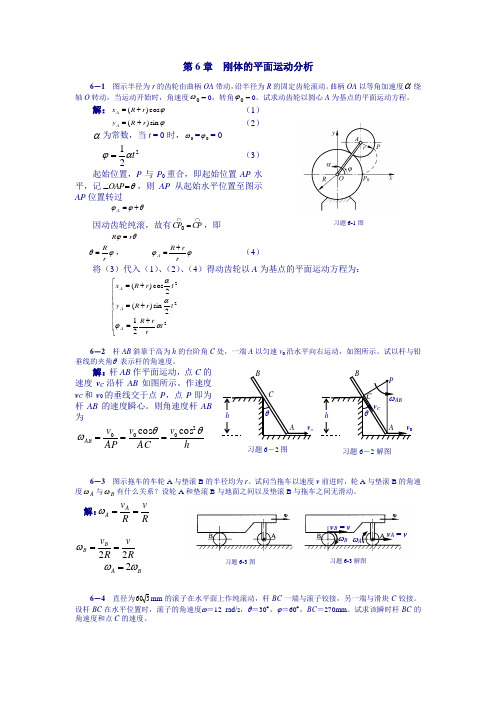
第6章 刚体的平面运动分析6-1 图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动,当运动开始时,角速度0ω= 0,转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解:ϕcos )(r R x A += (1) ϕsin )(r R y A +=(2)α为常数,当t = 0时,0ω=0ϕ= 0 221t αϕ=(3)起始位置,P 与P 0重合,即起始位置AP 水平,记θ=∠OAP ,则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚,故有⋂⋂=CP CP 0,即 θϕr R = ϕθr R =, ϕϕrr R A += (4)将(3)代入(1)、(2)、(4)得动齿轮以A 为基点的平面运动方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6-2 杆AB 斜靠于高为h 的台阶角C 处,一端A 以匀速v 0沿水平向右运动,如图所示。
试以杆与铅垂线的夹角θ 表示杆的角速度。
解:杆AB 作平面运动,点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬心。
则角速度杆AB 为6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时,轮A 与垫滚B 的角速度A ω与B ω有什么关系?设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解:RvR v A A ==ωR v R v B B 22==ωB A ωω2=6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。
设杆BC 在水平位置时,滚子的角速度ω=12 rad/s ,θ=30︒,ϕ=60︒,BC =270mm 。
试求该瞬时杆BC 的角速度和点C 的速度。
hv AC v AP v ABθθω2000cos cos ===习题6-1图ABCv 0hθ习题6-2图PωABv CABCv ohθ习题6-2解图习题6-3解图习题6-3图v A = vv B = v ωAωB习题6-6图习题6-6解图解:杆BC 的瞬心在点P ,滚子O 的瞬心在点D BDv B ⋅=ωBPBD BP v B BC ⋅==ωω ︒︒⨯=30sin 27030cos 36012 rad/s 8=PC v BC C ⋅=ωm/s 87.130cos 27.08=︒⨯=6-5 在下列机构中,那些构件做平面运动,画出它们图示位置的速度瞬心。
(完整版)刚体的转动习题

04第四章刚体力学一、选择题:1、如图4-18所示,一圆盘绕通过盘心且与盘面垂直的轴 0以角速度针转动。
今将两大小相等、方向相反、但不在同一条直线上的力F 和盘面同时作用到圆盘上,则圆盘的角速度:[](A )必然减少 (B )必然增大(C )不会变化(D )如何变化,不能确定(C ) mg T 1 my T 2)R J B J yR关于刚体对轴的转动惯量,下列说法中正确的是只取决于刚体的质量,与质量的空间分布和轴的位置无关. 取决于刚体的质量和质量的空间分布,与轴的位置无关. 取决于刚体的质量、质量的空间分布和轴的位置.只取决于转轴的位置,与刚体的质量和质量的空间分布无关.2、如图4-17所示,一质量为m 的匀质细杆 AB , A 端靠在粗糙的竖直墙壁上, 端置于粗糙的水平地面上而静止,杆身与竖直方向成 角, 大小为:[ ] BB 则A 端对墙壁的压力 3、 (A) 1 mgcos (B ) - mgtg (C ) mgsin 2(D )不能唯一确定 图 4-17某转轮直径 d 0.4m ,以角量表示的转动方程为 t * *3 *2 3t 4t (SI ),则: (A ) (B ) (C ) (D ) 从t 从t 在t 在t 2s 到t 4s 这段时间内,其平均角加速度为 2s 到t 4s 这段时间内,其平均角加速度为 2s 时,轮缘上一点的加速度大小等于 2s 时,轮缘上一点的加速度大小等于 6rad.s 2 ; 12rad .s 2 ; 3.42m.s 2 ; 26.84m.s 。
4、 轮 动过程中,下列哪个方程能成立? (A ) mg ky倔强系数为 k 的弹簧连接一轻绳,绳子跨过滑m 的物体,问物体在运 ] T 2如图4-2所示, (转动惯量为 J ),下端连接一质量为 [ (B) mg T 2 0Z图4-25、(A) (B ) (C ) (D) 6、 有两个力作用在一个有固定转轴的刚体上:(1) (2) (3) (4)[B 环的质量分布不(C) J A = J B .(D)不能确定J A 、J B 哪个大.&一力F (3i 5j)N ,其作用点的矢径为 r (4i 3j)m ,则该力对坐标原点的力矩 为:[] (A ) 3kN m (B )29kN m 9、一圆盘绕过盘心且与盘面垂直的光滑固定轴 向转动.若如图所示的情况那样, (C ) 19kN m O 以角速度按图示方 将两个大小相等方向相反但不在同一 (D) 3kN m 条直线的力F 沿盘面同时作用到圆盘上,则圆盘的角速度 (A)必然增大. (B)必然减少. (C)不会改变. (D)如何变化,不能确定. 10、均匀细棒OA 可绕通过其一端 O 而与棒垂直的水平固定光滑轴转 动,如图所示.今使棒从水平位置由静止开始自由下落,在棒摆动到 竖直位置的过程中,下述说法哪一种是正确的? 角加速度从大到小. 角加速度从小到大. 角加速度从大到小. 角加速度从小到大. Q 、R 、S 是附于刚性轻杆上的四个质点, (A) (B) (C) (D) 角速度从小到大, 角速度从小到大, 角速度从大到小, 角速度从大到小, Og11、如图4-19所示P 、 PQ QR RS则系统对00轴的转动惯量为:[ ] (A) 50ml 2(C ) 10ml 2 (B) 14ml 2 (D ) 9ml 24m oP3m OQ 图 4-192m mR So 12、如图4-1所示, A 、B 为两个相同的绕着轻绳的定滑轮, 一质量为M 的物体, B 滑轮受拉力F ,而且F Mg 。
刚体定轴转动练习题及答案

刚体定轴转动练习题一、选择题1、一刚体以每分钟60转绕Z 轴做匀速转动(ωϖ沿Z 轴正方向)。
设某时刻刚体上一点P 的位置矢量为k j i r ϖϖϖϖ543++=,其单位为m 210-,若以s m /102-为速度单位,则该时刻P 点的速度为:( ) A υϖ=94.2i ϖ+125.6j ϖ+157.0k ϖ; B υϖ=34.4k ϖ; C υϖ=-25.1i ϖ+18.8j ϖ; D υϖ=-25.1i ϖ-18.8j ϖ;2、一均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动,如图所示。
今使棒从水平位置由静止开始自由下落,在棒摆动到竖直位置的过程中,下述说法哪一种是正确的?( )A 角速度从小到大,角加速度从大到小。
B 角速度从小到大,角加速度从小到大。
C 角速度从大到小,角加速度从大到小。
D 角速度从大到小,角加速度从小到大。
3、刚体角动量守恒的充分而必要的条件是:( )A 刚体不受外力矩的作用B 刚体所受合外力矩为零C 刚体所受的合外力和合外力矩均为零D 刚体的转动惯量和角速度均保持不变4、某刚体绕定轴做匀变速转动时,对于刚体上距转轴为r 出的任一质元m ∆来说,它的法向加速度和切向加速度分别用n a 和t a 来表示,则下列表述中正确的是 ( )(A )n a 、t a 的大小均随时间变化。
(B )n a 、t a 的大小均保持不变。
(C )n a 的大小变化, t a 的大小恒定不变。
(D )n a 的大小恒定不变, t a 的大小变化。
5、有两个力作用在一个有固定转轴的刚体:(1)这两个力都平行于轴作用时,它们对轴的合力矩一定是零;(2)这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;(3)当这两个力的合力为零时,它们对轴的合力矩也一定是零;(1) 当这两个力对轴的合力矩为零时,它们的合力也一定是零。
A 只有(1)是正确的。
B (1),(2)正确,(3),(4)错误。
沪科版八年级物理第六章测评含答案

第六章测评(时间:45分钟满分:100分)一、选择题(本大题共5小题,每小题6分,共30分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.马拉着木柱前进(如图所示),使木柱前进的力的施力物体与受力物体分别是()A.地球和木柱B.马和木柱C.地面和木柱D.木柱和马2.关于物体所受重力的方向,下列表示正确的是()3.判断物体受力情况的时候,下列分析正确的是()A.只要物体相互接触,一定有相互作用的弹力B.地球表面一切物体都要受到重力C.静止在粗糙水平面上的物体一定受到摩擦力的作用D.做匀速直线运动的物体一定不受外力作用4.如图所示,一物体挂在弹簧测力计的下端,物体对弹簧测力计拉力的大小为()A.4.4 NB.3.9 NC.3.6 ND.3.3 N5.如图所示的四个实例中,目的是减小摩擦的是()二、填空题(每空3分,共33分)6.在春季运动会上,一个同学吹气球时发现:用手轻轻一压,气球就变扁了,说明力可以改变;用手轻轻一推,气球就向一侧飞走了,说明力可以改变。
7.甲、乙两同学的质量之比是10∶9,则他们的重力之比是,若甲同学的质量为50 kg,则其重力是,则乙同学的重力为。
8.汽车在紧急刹车过程中总要滑行一段距离才能停下来。
当雨天路面有水时,轮胎与地面间的摩擦变,在同样车速条件下,汽车紧急刹车后滑行的距离比路面没有水时变,因此司机驾车要注意“雨天路滑,小心慢行”。
9.如图所示,利用弹簧测力计拉着物体在水平面上匀速向右运动,该物体受到的摩擦力为N。
当弹簧测力计的示数增大为4 N时,该物体受到的摩擦力为 N。
10.右图所示为用筷子提米实验,杯中装满米,再加少许水,压紧,过一会儿提起筷子,米和杯也能够被提起,这是因为作用的结果,米所受摩擦力的方向是。
三、作图题(每题5分,共10分)11.踢足球是青少年喜爱的一项体育运动。
如图所示是向斜上方飞出的足球,不考虑空气阻力,请你画出足球所受力的示意图。
12.装卸工人利用斜面将一木箱推到汽车上(如图)。
刚体考试题及答案

刚体考试题及答案一、选择题(每题2分,共20分)1. 刚体的转动惯量是关于旋转轴的()。
A. 常数B. 函数C. 随机变量D. 无规律变化答案:A2. 刚体绕固定轴的转动惯量I与质量M和半径r的关系是()。
A. I = Mr^2B. I = 2MrC. I = MrD. I = 1/2Mr^2答案:D3. 刚体的平移运动和转动运动的合成是()。
A. 平移运动B. 转动运动C. 螺旋运动D. 不确定答案:C4. 刚体的角速度和线速度的关系是()。
A. 线速度是角速度的两倍B. 线速度是角速度的一半C. 线速度与角速度成正比D. 线速度与角速度无关答案:C5. 刚体的角动量守恒的条件是()。
A. 外力矩为零B. 外力为零C. 外力矩和外力都为零D. 外力矩和外力都不为零答案:A6. 刚体的动能与()有关。
A. 质量B. 速度C. 转动惯量D. 所有以上因素答案:D7. 刚体的角加速度与()有关。
A. 外力矩B. 转动惯量C. 角速度D. 所有以上因素答案:A8. 刚体的进动角速度与()有关。
A. 外力矩B. 转动惯量C. 角速度D. 所有以上因素答案:D9. 刚体的章动周期与()有关。
A. 转动惯量B. 外力矩C. 角速度D. 所有以上因素答案:A10. 刚体的自由振动的周期与()有关。
A. 转动惯量B. 外力矩C. 角速度D. 所有以上因素答案:A二、填空题(每题2分,共20分)1. 刚体的转动惯量是关于旋转轴的________。
答案:常数2. 刚体绕固定轴的转动惯量I与质量M和半径r的关系是I = ________。
答案:1/2Mr^23. 刚体的平移运动和转动运动的合成是________。
答案:螺旋运动4. 刚体的角速度和线速度的关系是线速度与角速度________。
5. 刚体的角动量守恒的条件是外力矩________。
答案:为零6. 刚体的动能与________有关。
答案:所有以上因素7. 刚体的角加速度与________有关。
刚体的转动部分习题分析与解答

动轨迹为一个圆弧。
刚体的定轴转动和平面转动的比较
03
定轴转动和平面转动是刚体转动的两种基本形式,它们在运动
学和动力学上有一些不同之处,如角速度、角加速度等。
03
刚体的动能与势能
刚体的动能
总结词
刚体的动能是指刚体在转动过程中所 具有的能量,与刚体的转动速度和质 量分布有关。
详细描述
刚体的动能计算公式为$E_{k} = frac{1}{2}Iomega^{2}$,其中$I$为刚体的转 动惯量,$omega$为刚体的角速度。转动惯量 是描述刚体质量分布对其转动影响的物理量, 与刚体的质量分布、形状和大小有关。
解答过程
钢球下落过程中,其速度逐渐增大,故其动能在 不断增加。同时,钢球离地面的高度逐渐减小, 故其势能在不断减小。由于钢球下落过程中只有 重力做功,故其机械能守恒。
习题五:关于刚体的机械能守恒的题目
总结词
理解机械能守恒的概念,掌握机械能守恒的条件和机械能守恒的计算方法。
详细描述
机械能守恒是指系统内各种形式的能量在相互转化时总量保持不变。对于刚体系统,只有重力或弹力 做功时机械能守恒。机械能
刚体的势能
总结词
刚体的势能是指刚体在转动过程中相对于某一参考点所具有 的能量。
详细描述
刚体的势能计算公式为$U = -GMmcostheta$,其中$G$为万 有引力常数,$M$和$m$分别为两个质点的质量,$theta$为 两质点连线和垂直于势能参考平面的夹角。对于刚体,势能的 具体值取决于参考点的选择。
实际问题。
习题五解答与解析
要点一
总结词
刚体的角动量守恒
要点二
详细描述
这道题目考察了学生在刚体转动中如何应用角动量守恒的 知识。学生需要理解角动量的概念,知道角动量等于刚体 的转动惯量乘以角速度,并能够根据角动量守恒的条件判 断刚体的运动状态。
刚体定轴转动练习题及答案

刚体定轴转动练习题一、选择题1、一刚体以每分钟60转绕Z 轴做匀速转动(ωϖ沿Z 轴正方向)。
设某时刻刚体上一点P 的位置矢量为k j i r ϖϖϖϖ543++=,其单位为m 210-,若以s m /102-为速度单位,则该时刻P 点的速度为:( ) A υϖ=94.2i ϖ+125.6j ϖ+157.0k ϖ; B υϖ=34.4k ϖ; C υϖ=-25.1i ϖ+18.8j ϖ; D υϖ=-25.1i ϖ-18.8j ϖ;2、一均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动,如图所示。
今使棒从水平位置由静止开始自由下落,在棒摆动到竖直位置的过程中,下述说法哪一种是正确的?( )A 角速度从小到大,角加速度从大到小。
B 角速度从小到大,角加速度从小到大。
C 角速度从大到小,角加速度从大到小。
D 角速度从大到小,角加速度从小到大。
3、刚体角动量守恒的充分而必要的条件是:( )A 刚体不受外力矩的作用B 刚体所受合外力矩为零C 刚体所受的合外力和合外力矩均为零D 刚体的转动惯量和角速度均保持不变4、某刚体绕定轴做匀变速转动时,对于刚体上距转轴为r 出的任一质元m ∆来说,它的法向加速度和切向加速度分别用n a 和t a 来表示,则下列表述中正确的是 ( )(A )n a 、t a 的大小均随时间变化。
(B )n a 、t a 的大小均保持不变。
(C )n a 的大小变化, t a 的大小恒定不变。
(D )n a 的大小恒定不变, t a 的大小变化。
5、有两个力作用在一个有固定转轴的刚体:(1)这两个力都平行于轴作用时,它们对轴的合力矩一定是零;(2)这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;(3)当这两个力的合力为零时,它们对轴的合力矩也一定是零;(1) 当这两个力对轴的合力矩为零时,它们的合力也一定是零。
A 只有(1)是正确的。
B (1),(2)正确,(3),(4)错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 刚体转动自测题答案
一、选择题答案 1、(C ) 2、(B ) 3、(B ) 4、(C ) 5、(C ) 6、(D ) 7.(B ) 8、(B) 9、(D ) 10、(A ) 11、(C ) 12、(B) 13、(B) 14、(C ) 15、(A) 16、(C) 17、(C) 18、(D ) 19、(C) 20、(D) 21、(C)
二、填空题答案
1、1 ;
2、3 ;
3、变化 ;
4、合外力矩 ;
5、合外力矩 ;
6、mL 2/12;
7、mL 2
/3 ;8、mr 2
/2; 9、ω2; 10、不变 ; 11、0; 12、3g/2l ; 13、0 ;
14、mgl/2 ; 15、ml 2ω/3 。
三、计算题
1.一半径为 0.3m 的转轮作匀角加速度转动,其初角速度ω0=0.5π rad·s -1,在t =10 s 时,其角速度ω=6.5π rad·s -1,求:(1)在t =10 s 时,转轮转过的角度;(2) t =10 s 时,转轮边沿点的切向速度、切向加速度和法向加速度各为多少? 解:(1)由于转轮做匀角加速度转动,因此根据公式有
t βωω+=0 (2分)
2002
1t t βωθθ++= (2分)
可得到t =10 s 时转轮转过的角度为0θθθ-=∆=35πrad 。
(2分) (2)切向速度的大小为
πω95.1==r v m/s (2分)
切向加速度为
πβτ18.0===r dt
dv a m/s 2 (2分)
法向加速度
222
7.12πω===r r
v a n m/s 2 (2分) 2.如图所示,一根长为l 、质量为m 的均匀细直棒可绕其一端在竖直面内自由转动,开始时棒处于水平位置,求棒转到与水平线成角度θ 时的角加速度和角速度。
(细棒对转轴的转动惯
量为23
1
ml J =)
解:棒所受合外力矩 θcos 2
1
mgl M = (3分)
由转动定律得角加速度
图
l g ml mgl J M 2cos 33
1cos 21
2θθβ=
== (3分) 因为 θω
ω
θθωωβd d dt d d d dt d === (2分) 所以 ⎰⎰=θωθθ
ωω002cos 3d l g d (3分)
l
g θ
ωsin 3=
(1分)
3.如图所示,一匀质细杆质量为m ,长为l ,可绕过一端O 的水平轴自由转动,杆于水平位置由静止开始摆下。
求:(1)初始时刻的角加速度;(2)杆转过θ角时的角
速度。
(细棒对转轴的转动惯量为23
1
ml J =)
解: (1)由转动定律,有
β)31
(22ml l mg = (4分) l g
23=β (2分)
(2)由机械能守恒定律,有
2
2)3
1
(21sin 2ωθml l mg =
(4分)
l
g θ
ωsin 3=
(2分)
4.如图所示,一匀质细杆质量为m ,长为l ,可绕过一端O 的水平轴自由转动,杆由水平位置由静止开始摆到竖直位置。
试证明, 杆在下摆过程中,角加速度越来越小,角速度越来越大。
证明:当杆转过θ角时,棒所受合外力矩
θcos 2
1
mgl M = (2分)
由转动定律得角加速度
l g ml mgl J M 2cos 33
1cos 21
2θ
θβ=
== (2分) 可得,杆由水平位置摆到竖直位置过程中,角加速度β随θ角的增大而增小。
图
图
因为 θω
ω
θθωωβd d dt d d d dt d === (2分) 所以 ⎰⎰=θωθθ
ωω002cos 3d l g d (2分)
l
g θ
ωsin 3=
(2分) 可得,杆由水平位置摆到竖直位置过程中,角速度ω随θ角的增大而增大。
5.如右图所示,质量为M ,长为l 的直杆,可绕O 无摩擦地转动。
设一质量为m 的子弹沿水平方向飞来,恰好射入杆的下端,若直杆(连同射入的子弹)的最大摆角为060=θ,试证明子弹速度大小为()()2
0632m
gl
M m M m v ++=。
证:碰撞过程中,系统角动量守恒
ω)3
1
(220Ml ml l mv += (5分)
上摆过程中,系统机械能守恒。
取直杆下端为势能零点,则
)60cos 21
1()60cos 1()31(21200222-+-=++Mgl mgl Ml ml l Mg ω (5分)
可证得:()()2
0632m
gl
M m M m v ++=
(2分)
6.计算如图所示系统中物体的加速度.设滑轮为质量均
匀分布的圆柱体,其质量为M ,半径为r ,在绳与轮缘的摩擦力作用下旋转,且绳子与滑轮之间无相对滑动,忽略桌面与物体间的摩擦,设1m =50kg ,2m =200 kg,M =15 kg, r =0.1 m,滑轮的转动惯量22
1Mr J =
,g=9.8 m/s 2。
解: 分别以1m ,2m 滑轮为研究对象,对1m ,2m 运用牛顿定律,有
a m T g m 222=- ① (3分)
a m T 11= ② (3分)
对滑轮运用转动定律,有
β)2
1
(212Mr r T r T =- ③
(3分)
图
βr a = ④ (2分) 联立以上4个方程,得
2212s m 6.72
15
20058
.92002-⋅=+
+⨯=++=M m m g m a (1分)
7.有一倾角为θ的斜面,其上装一定滑轮,一软细绳跨过滑轮,两端分别接两物体A 和B ,A 与B 的质量皆为m ,设A 与斜面间是光滑的,绳与滑轮无相对滑动,轮轴无摩擦力,滑轮的转动惯量为J ,求物体下降的加速度。
解:对B 物体受力分析 ma T mg =-1 (3分)
对A 物体受力分析ma mg T =-θsin 2 (3分) 对滑轮受力分析 ()βJ r T T =-21 (3分) 由于 βr a = (2分)
解得 2
2
22sin mr J r mg mgr a +-=θ (1分)
8.有一质量为M 、半径为R 的均匀圆盘,以角速度ω0旋转着,某时刻,有一质量为m 的小碎块从其边缘飞出,方向正好竖直向上,求:⑴ 小碎块能上升的最大高度;⑵ 破裂后圆盘的角速度和角动量。
解:(1)设物体能飞起的高度为h ,由机械能守恒定律得,碎片飞出时的角速度为0ω,碎片转动惯量为m J ,可得 2
2
1ωm J mgh =
(2分) 2mR J m = (2分) 解上两式得:h =g
R 22
2ω (2分)
(2)设余下部分的角速度为'ω,圆盘总的转动惯量为22
1MR J =,余下部分对转轴的
转动惯量为m J J -。
则在碎片飞出的瞬间碎片和所剩部分对转轴的角动量守恒,由角动量守恒定律得,
')(00ωωωm m J J J J -+= (2分) 解上式得:0'ωω= 即角速度不变。
(2分)
余下部分角动量为:=L ')(ωm J J -=022)2
1
(ωmR MR - (2分)
9.如右图所示,有一长l 的均匀细杆,其质量为M ,杆的一端
固定在过O 点的光滑水平轴上并可在竖直面内自由地转动。
开始时
使细杆静止在竖直位置处,现让一质量m 的子弹以速度v 0的速率射
入细杆并留在杆中,子弹的速度沿水平方向,射入点距O 点的距离d 。
求:⑴ 子弹停在杆中时,杆和子弹共同运动的角速度;⑵ 杆能偏转的最大角度。
解:⑴ 设子弹停在杆中时,杆和子弹共同运动的角速度为ω,对于子弹、杆组成一系统,应用角动量守恒,有 ω)3
1
(220md Ml d mv += (5分) 即 22
03
1md Ml d mv +=
ω (1分)
⑵ 设杆能偏转的最大角度为θ,子弹射入杆后,以子弹、细杆和地球为系统,系统机械能守恒,故
)cos 1(2
)cos 1()31(21222θθω-+-=+l
Mg mgd md Ml (5分) )
3
1)(2(211cos 22
2
202md Ml mgd l Mg d v m ++-
=θ ])
31)(2(211arccos[2
22
202md Ml mgd l Mg d v m ++-=θ (1分)。
