3.1原子之间的互作用
3.1 一维单原子链
一维无限原子链 —— 每个原子质量m，平衡时原子间距a —— 原子之间的作用力 第n个原子离开 平衡位置的位移 第n个原子和第n＋1 个原子间的相对位移
第n个原子和第n＋1个原子间的距离
03_02_一维单原子链 —— 晶格振动与晶体的热学性质
平衡位置时，两个原子间的互作用势能
发生相对位移
后，相互作用势能
a
a
—— 只研究清楚第一布里渊区的晶格振动问题 —— 其它区域不能提供新的物理内容
03_02_一维单原子链 —— 晶格振动与晶体的热学性质
玻恩－卡门（Born-Karman）周期性边界条件 —— 一维单原子晶格看作无限长，所有原子是等价的，每个 原子的振动形式都一样 —— 实际的晶体为有限，形成的链不是无穷长，链两头的 原子不能用中间原子的运动方程来描述
2 4 sin 2 ( aq )
m
2
格波的波速
—— 波长的函数
—— 一维简单晶格中格波的色散关系，即振动频谱
格波的意义
连续介质波
波数 q 2
—— 格波和连续介质波具有完全类似的形式
—— 一个格波表示的是所有原子同时做频率为的振动
03_02_一维单原子链 —— 晶格振动与晶体的热学性质
n Aei(tnaq) —— 简谐近似下，格波是简谐平面波
§3.1 一维单原子链
绝热近似 —— 用一个均匀分布的负电荷产生的常量势场来 描述电子对离子运动的影响 —— 将电子的运动和离子的运动分开 晶格具有周期性，晶格的振动具有波的形式 —— 格波 格波的研究 —— 先计算原子之间的相互作用力 —— 根据牛顿定律写出原子运动方程，最后求解方程
03_02_一维单原子链 —— 晶格振动与晶体的热学性质
3.1一维晶格振动
2 n Ae
2 n1 Bei[t ( 2 n1) aq]
2.色散关系
把上面两个解带入下列方程组：
m 2 n ( 2 n 1 2 n 1 2 2 n ) M 2 n 1 ( 2 n 2 n 2 2 2 n 1 )
..
2n n1 n1 n1 n1 2n
每个原子对应一个方程，若原子链有N个原子，则有N个方
程，上式实际上代表着N个联立的线性齐次方程。
下面将验证方程具有格波形式的解。给出试探解：
nq Aei (t naq )
其中ω，A为常数。
π π q a a
n n N
晶格振动波矢的数 目=晶体的原胞数
3.1.2 一维双原子链(复式格)的振动
1. 运动方程和解 (1) 模型:一维无限长原子链，可以看作是最简单的复式 晶格：每个原胞含有两个不同的原子P、Q，质量为m和M，且 m<M。相邻原子间距均为a，(晶格常量为2a )恢复力系数为。 2n-2 2n-1 2n P 2n+1 2n+2
第n-2个原子
第n-1个原子
第n个原子
第n+1个原子
第n+2个原子
a
μn-2
μn-1
μn
μn+1
μn+2
用…μn-1、 μn、 μn+1 …分别表示序号为… n-1、 n、 n+1 …原 子在t时刻偏离平衡位置的位移。 (2)振动方程和解 假设只有近邻原子间存在相互作用，r=a+δ。其中δ表示 对平衡位置a的偏离。 u（r）为原子间的互作用势能。
固体物理答案第三章1
Ae i ωt naq
Be i ωt naq
2n i ωt a b q 2
将 x 2n , x 2n 1 的值代回方程得到色散关系
β1 β 2 ω 2mM
2
m M
3.3 一维复式格子，原子质量都为m,晶格常数为a，任一个原
子与最近邻原子的间距为b,若原子与最近邻原子和次近邻原子 的恢复力常数为 β 和 β ，试列出原子的运动方程并求出色散 关系。
1
2
3
n-1
n a
n+1 n+2
N-1 N
解： 此题为一维双原子链。设第 n 1, n, n 1, n 2 个原子的 位移分别为 un1 , un , un1 , un 2 。第 n 1 与第 n 1 个原子属 于同一原子，第 n 与第 n 2 个原子属于同一原子，于是
m M
2
16mMβ1 β2 2 aq sin 2 2 β1 β 2
（2）（a）当上式取‘+’号时为光学波 β1 β 2 8mMβ1 β2 2 2 1 cosaq ωo m M m M 2 2mM β1 β 2
2 1 2 2 1 iqa 2 2 1 1 2
由于A和B不可能同时为零，因此其系数行列式必定为零，即
β β mω β β e 0 β β mω β β e
2 iqa 1 2 2 1 iqa 2 2 1 1 2
解上式可得
12 2 β1 β2 2m 4m2 16m β1 β2 sin2 qa 2 ω 2 2 2m β1 β2 2 12 β1 β2 1 1 4β1 β2 sin2 qa 2 m 2 β1 β2
原子间相互作用势解读
原子间相互作用势解读原子间相互作用势是描述两个或多个原子之间相互作用力的函数。
它是描述原子、分子或固体材料性质的关键因素，对于理解化学反应、材料力学性能、相变、晶体结构等都起着重要的作用。
本文将对原子间相互作用势进行解读。
一种显著的原子间相互作用势是范德华力(Van der Waals forces)，它是由电荷偶极、氢键、格列高利亚力和弥散力等组成。
这些力可以通过公式来描述，例如Lennard-Jones势能公式：V(r)=4ε[(σ/r)^12-(σ/r)^6]这个公式中，r是两个原子间的距离，ε和σ是相互作用的参数。
这个公式表示了势能和原子间距离的关系，当两个原子非常接近时，势能会变得非常大，当原子间距离较大时，势能会变得非常小。
除了范德华力，库仑力也是原子间相互作用势的重要组成部分。
库仑力是由原子间的电荷交互作用引起的，它可以通过库仑电势公式来描述：V(r)=k*q1*q2/r其中r是两个原子间的距离，q1和q2是原子的电荷，k是电常数。
这个公式表示，当两个原子带有相同的电荷时，它们之间会存在排斥力；当两个原子带有相反的电荷时，它们之间会存在吸引力。
除了范德华力和库仑力，还有其他一些原子间相互作用势也非常重要。
例如，金属间相互作用势(Metal-Metal Interaction Potential)用于描述金属之间的相互作用力，分子间相互作用势(Molecule-Molecule Interaction Potential)用于描述分子之间的相互作用力。
通过使用原子间相互作用势，我们可以研究原子间的排列方式和结构稳定性。
例如，在材料科学中，人们可以使用原子间相互作用势预测材料的熔点、弹性模量、黏度等性质。
在化学反应中，通过分析原子间相互作用势，我们可以了解反应的速率和过程。
虽然原子间相互作用势是描述原子间相互作用的重要工具，但是它并不是完美的。
由于原子间相互作用力很复杂，我们通常只能采用近似的方法来描述这些力。
固体物理学第三章
3 1 !(d d 3 U 3)r a 3 ..... .n 1 !.(d d .n U .n)r .a.n
简谐近似—— 振动很微弱，势能展式中只保留到二阶项。
U (r) U (a ) (d)U 1(d 2 U ) 2 da r 2 !d2ra U(r)U(a)1 2(dd2U 2r)a2
此处N=5,代入上式即得：
ei(5a)q 1 5aqn2（n为整数）
由于格波波矢取值范围：
q
a
a
则：5n5
22
故n可取－2，－1，0，1，2这五个值
相应波矢：4,2,0,2,4
5a 5a 5a 5a
由于，2 sinqa
m2
代入，β，m及q值 则得到五个频率依次为（以rad/sec为单位） 8.06×1013，4.99×1013，0，4.99×1013，8.06×1013
f du(d2u) d 2u 为恢复力常数
dr d2r
dr 2
周期边界条件
N 2 a l q l 为 整 N /2 h N 数 /2 且
3.1 一维单原子链的振动
3.1.1 一维单原子链的振动
设原子链为一维，则：原子间距为a; 第n个原子的平衡位置为rn=na 第n个原子离开平衡位置的位移为xn
格波的应用：
晶体的弹性力常数β约为15N/m，若一个原 子的质量为6×10-27Kg，则晶格振动的最大圆频 率为ωm=1014弧度/秒，最大频率γm约为1013Hz即 10THz。THz波段在微波与红外光之间。
不同材料的晶格振动频谱具有各自的特征， 可以作为这个材料的 “指纹”，THz谱技术作为 一种有效的无损探测方法，通过晶格振动频谱可 以鉴别和探测材料。
3.1.2 格波频率与波矢关系——色散关系
3.1一维晶格振动
aq 2 sin m 2
可以发现，上面的解与n无关，表明N个联立方程都归结
为同一个方程。只要ω与q之间满足上式的关系，我们给定的
试探解就表示了联立方程的解。 通常把ω与q之间的关系称为色散关系。或者把ω(q)作为q的
函数称为晶格振动谱，可以通过实验的方法测得或根据原子
间相互作用力的模型从理论上进行计算。
§3.1 一维晶格的振动
3.1.1 一维单原子链的振动
晶格具有周期性，因此晶格的振动模具有波的形式， 称为格波。格波和一般连续介质波有共同的特征，但也有
它不同的特点。
1.一维单原子链的振动方程及其解
(1)模型：一维无限长的单原子链，原子间距为a（即
原胞体积为a），原子质量为m。原子限制在沿链的方向 运动。原子间的力常数均为β。
u (r ) u (a )
按一般简谐振动把近似互作用能保留到二次项
1 d 2u 2 du u (r ) u (a) 2 2 dr a dr a 2 du d u 在上式中 0, 2 dr a dr a
2n
Q原子： M
2n1 2n1 22n
2 n 1
2 n 1 2 n 2 2 n 1 2 n
2n2 2n 22n1
上面两个方程是原子运动的典型方程，当原子链包含N个原胞
π π q a a
上述q以外的值，并不能提供其它不同的波。
格波波数q的不唯一性特点可以如图说明：
a
4a
μ
a
4a 5
q 2a
5 xq 2a
双原子之间的作用力
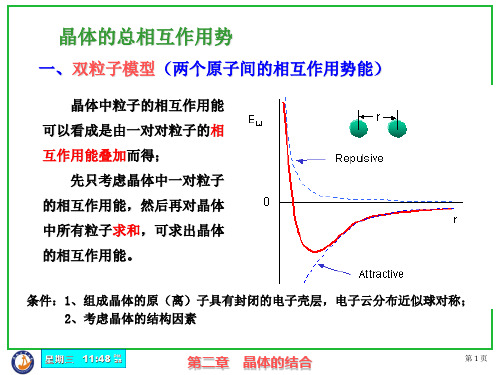
r r0 du (r ) 0 dr r0
第二章 晶体的结合
第 14 页
f (r0 ) 0
r0
n m
Bn Am
(2) (3)
A m U C U (r0 ) m (1 ) r0 n
互作用势能达极小值，由此决定原子
间的平衡距离r0。
此时的状态称为稳定状态。
荷间的库仑吸引力，长程作用； +B/rn :代表排斥能，来自同性电荷 间的库仑斥力及泡利原理所引起的 排斥力，总体表现短程作用。
第二章
晶体的结合
第 13 页
相互作用势能的一般性质
（1）平衡位置r0的确定： 图（a）：互作用势能曲线
图（b）: 互作用势能曲线的微商曲线
du( r ) mA nB f (r ) m 1 n 1 dr r r
1 k V
第二章
V P
T
第 12 页
晶体的结合
1、三维晶体参数与结合能的关系
相距r的两个原子之间的互作用势能用U(r)表示：
A B U (r ) m n r r
A、B、m、n皆为大于零的常数。
(1)
( m n)
-A/rm :代表吸引能，来自异性电
这表明，分子间的范德瓦尔斯－伦敦力引起的互作用势能与r-6成正比。 而由泡利原理产生的斥力作用，较难计算，一般由实验求得，排斥 势与r-12成反比 因此，一对分子间总的互作用势能为：
第二章
晶体的结合
第9页
Page 10
A B u( r ) 6 12 (11) r r or
12 6 u( r ) 4 (12) r r A2 B , 4B A
第三章铁液中溶质的相互作用参数,重做后2汇总
定义：
1 2 ln 2 (2) ( ) x1 1 2 2 2 x2
1 2 ln 2 (3) ( ) x 1 2 2 x32 1
1 2 ln 2 (i ) ( ) x1 1 2 2 2 xi
2 ln 2 (2,3) ( ) x1 1 2 x2x3
lg f 2 lg f 2' lg f 23
•或
就是
__ (%2) __ (%3)
2 3 lg f 2 e2 [%2] e2 [%3]
两边同乘以2.303RT
2.303RT lg f2 2.303RT lg f2' 2.303RT lg f 23
E 2 3 mixG2 2.303RTe2 [%2] 2.303RTe2 [%3]
2 2 2 2
如图3-1所示：
ln
2 0 2
2 2 2 x2
2 2 x2
x2
图3－1 相互作用系数的几何描述
在以上图中，虚线是线性关系，表示 ln
2 2 0 与 x 的线 2 2 2
性关系段 ln( 2 / 20 ) 22 x2 ；实线是非线性关 2 2 0 2 2 2 系 ln( 2 / 2 ) 2 x2 2 x2 ，其中 2 x2 是虚线与实线之间 距离，是非线性程度的描述。可以看出，随着浓度 与x 的关系偏离线性关 2 2 x2的增大， 2 x2 越来越大， ln 2 2 0 2 系的程度在增大。
对二元系： 1-2 ，组元 1-溶剂，组元 2-溶质，设其 ' ' ' a a 活度为 2 ， 2 2 x2 而对三元系：1-2-3，组元1-溶剂，组元2，3-溶质， 则组元2的活度设二元系中的x2同三元系中的x2相同。 则一般地 a2 2 x2
第三章 晶体中的原子热振动 PPT课件
dU r 0 U a dr r a
U a
晶体的结合能
i , j =1 , 2 , , N
二. 原子间的键
1. 离子键 离子键是由正负离子通过库仑引力形成的。典型的如ⅠA族元素 (碱金属)与ⅦB族元素(过渡金属锰族元素：锰、铼、锝)之间形 成。ⅠA族元素易于失去电子而带正电荷，ⅦB族元素倾向于得 到一个电子而带负电荷，并使两者的电子组态都变为满壳层。
短波近似
满足力的平衡条件，质心基本不动。 以同一振幅刚性地振动。
q
2a
A
B A
B
0
即A B 即A B
质量小的原子对短光学 波贡献大。
质量大的原子对短声学 波贡献大。
4. 周期性边界条件 设晶体由N个原胞构成，则周期性边界条件为：
﹡ 各原子振动间存在相互联系，有固定的位相差。相邻原子
的位相差为qa
﹡﹡ xm xn时
Aeiqmat Aeiqnat
则, ma na 2 l l取整数
q
(3) 在不同时间观察整个晶格
整个晶格的振动（原子振动的集体行为），构成了一个波矢
为 q的前进波———格波。
mM
3. 声学波与光学波
2
mM mM
1
1
4mM
m M 2
sin 2
aq
1 2
从相邻原子的振幅比来讨论声学波与光学波的特点：
从前面的方程组
m2 2
A 2 cos qa B 0
，得：
2 cos qa A M2 2 B 0
材料科学化学键
§3 化学键3.1 原子间的相互作用当两个原子相互靠近时，它们之间存在的相互作用力包括原子核与核外电子之间的吸引力，以及原子核、核外电子之间的排斥力。
这种原子之间的相互作用可用图2.2表示，在某一间距r0处，吸引力和排斥力达到平衡，势能最低，原子最稳定。
图2.4 两个原子之间的相互作用力、势能与原子间距的关系由于核外电子，特别是价电子的不同，原子之间的结合方式（化学键）也不同,包括：依靠电子的转移或共享形成的强键（一次键）,如金属键,离子键,共价键；借分子之间的偶极吸引力而形成的弱键（二次键），如范德华（V an der waals）键、氢键。
3.2 金属键金属原子形成晶体时，金属中的自由电子为整个晶体所共有，可以在整个晶体中自由运动，失去价电子的金属正离子则在三维空间中作周期性排列，这种键合称为金属键。
金属键的主要特点是无饱和性和方向性，从而导致密堆结构和良好延展性；价电子的自由运动则使金属具有良好的导电和导热性能。
图2.5 金属键示意图3.3 离子键金属原子和非金属原子分别形成正离子和负离子，正、负离子相互吸引结合在一起形成离子晶体，这种键合称为离子键。
由离子键构成的化合物称为离子化合物，如NaCl等。
由于负离子的体积比正离子的体积大，所以离子化合物的晶体结构特点是：负离子在三维空间中作周期性排列，正离子占据负离子所形成的间隙。
离子键的特点是键合作用强、无方向性。
另外，由于很难产生自由运动的电子，离子化合物都是良好的电绝缘体。
但当处在高温熔融状态时，正负离子在外电场作用下可以自由运动，即呈现离子导电性。
图2.6 离子键示意图3.4 共价键两个或多个电负性相差不大的原子间通过共用电子对而形成的化学键即为共价键。
共价键特点是有饱和性和方向性，因此以共价键形成的晶体结构稳定、熔点高、坚硬无塑性，一般是绝缘体。
图2.7 共价键示意图3.5 范德华力在某一瞬间，一个原子（分子）的正负电荷重心可能不重合，从而形成小的偶极子。
原子间相互作用势解读
原子间相互作用势解读静电相互作用的形式可以用库伦定律来描述，即原子之间的电荷之间的相互作用力与它们之间的距离成反比。
具体来说，原子之间的相互作用势能可以表示为：V_Coulomb = k * (q1 * q2) / r其中，q1和q2是原子之间的电荷，r是它们之间的距离，k是一个常数。
范德华相互作用则更为复杂一些。
它可以用范德华力场模型来描述，其中最常用的是Lennard-Jones势函数。
Lennard-Jones势函数可以表示为：V_LJ=4ε[(σ/r)^12-(σ/r)^6]其中，ε是势能的尺度参数，σ是势能的距离参数，r是原子之间的距离。
Lennard-Jones势函数的形式可以分为两个部分：第一个部分是吸引项，即(σ/r)^12，它表示原子之间的瞬时电偶极引起的吸引力；第二个部分是排斥项，即(σ/r)^6，它表示原子之间的电子云重叠引起的排斥力。
这两个项的平衡决定了原子间的总体相互作用。
在实际应用中，原子间相互作用势通常还会加入其他修正项，以更准确地描述实际系统中的相互作用。
例如，对于离子化合物，静电相互作用势能可以通过考虑离子晶体间的库伦吸引力和斥力来表示。
而对于金属材料，电子间的交换和相关作用也需要被纳入考虑。
通过选择适当的参数，我们可以用原子间相互作用势来模拟和预测原子间的结合、位移和振动等行为。
这对于研究和理解固体材料的性质具有重要的意义。
例如，通过原子间相互作用势，我们可以解释和预测材料的热膨胀系数、热导率、机械性能等。
总而言之，原子间相互作用势是描述原子之间相互作用力的数学函数。
它包括静电相互作用和范德华相互作用，可以通过适当地选择参数来模拟和预测原子间的行为。
在分子动力学模拟和固体材料建模中具有广泛的应用。
高中物理必修一第三章相互作用知识点总结
高中物理必修一第三章相互作用知识点总结第一篇：高中物理必修一第三章相互作用知识点总结高中物理必修一第三章相互作用复习资料板块一：基本知识点一、重力，基本相互作用1、力和力的图示2、力的作用效果3、力是物体与物体之间的相互作用（1）、施力物体（2）受力物体（3）力的相互性（牛顿第三定律）4、力的三要素：大小，方向，作用点5、重力：由于地球吸引而受的力大小G=mg 方向:竖直向下重心：重力的作用点由物体形状和质量分布共同决定均匀分布均匀、形状规则物体：几何对称中心不一定在物体身上6、四种基本作用（记住）（1）万有引力（2）电磁相互作用（3）强相互作用（4）弱相互作用二、弹力1、性质：接触力2、弹性形变：当外力撤去后物体恢复原来的形状3、弹力产生条件（形变的物体是施力物体）（1）挤压（2）发生弹性形变4、方向：与形变方向相反（①按照接触类型分：3类；②绳、杆、弹簧）5、常见弹力（1）压力垂直于接触面，指向被压物体（2）支持力垂直于接触面，指向被支持物体（3）拉力：沿绳子收缩方向（4）弹簧弹力方向：可短可长沿弹簧方向与形变方向相反6、弹力大小计算（胡克定律）（实验）F=kx k 劲度系数 N/m x 伸长量三、摩擦力产生条件：两个物体接触且粗糙（有弹力）有相对运动或相对运动趋势静摩擦力：相对运动趋势不代表物体一定静止静摩擦力方向：沿着接触面与运动趋势方向相反大小：0≤f≤Fmax 大小的计算方法：平衡或牛顿第二定律滑动摩擦力：有相对滑动不代表物体一定运动大小：f＝μN（注意N不一定等于mg）N 相互接触时产生的弹力四、力的合成与分解（力的合成实验）实验方法：等效替代求合力方法：平行四边形定则（合力是以两分力为邻边的平行四边形对角线，对角线长度即合力的大小，方向即合力的方向）合力与分力的关系1、合力可以比分力大，也可以比分力小2、夹角θ一定，θ为锐角，两分力增大，合力就增大3、当两个分力大小一定，夹角增大，合力就增大，夹角增大，合力就减小（0＜θ＜π）4、合力最大值F=F1+F2 最小值F=|F1-F2|（思考三力合成的合力范围）力的分解：已知合力，求替代F的两个力原则：分力与合力遵循平行四边形定则本质：力的合成的逆运算作分力的基本操作：明确分力的方向——以合力为对角线分力为邻边构建平行四边形计算法求合力、分力的实质：解三角形（三角函数的运算）五、受力分析步骤和方法 1.步骤（1）研究对象：受力物体（2）隔离开受力物体（3）顺序：①场力（重力，电磁力......）②弹力：（绳子拉力沿绳子方向；轻弹簧压缩或伸长与形变方向相反；轻杆可能沿杆，也可能不沿杆；垂直于接触面）③摩擦力静摩擦力方向1.求 2.假设滑动摩擦力方向与相对滑动方向相反④其它力（题中已知力）（4）检验是否有施力物体六、摩擦力分析根据运动状态分析：根据平衡或牛顿第二定律分析七、重难点模型1、三力平衡模型2、斜拉模型3、斜面模型（见右图）斜面倾角θ动摩擦因系数μ=tanθ 物体在斜面上匀速下滑μ＞tanθ 物体保持静止μ＜tanθ 物体在斜面上加速下滑板块二：必须会做的题类型一：概念辨析1.如图，重力大小为G的木块静止在水平地面上，对它施加一竖直向上且逐渐增大的力F，若F总小于G，下列说法中正确的是A.木块对地面的压力随F增大而减小B.木块对地面的压力就是木块的重力C.地面对木块的支持力的大小等于木块的重力大小D.地面对木块的支持力的大小等于木块对地面的压力大小2.关于弹力的说法，错误的是：A.物质互相接触，就有弹力的相互作用。
量子光学 第一部分《原子与光场的相互作用》
（1）
i
(t ) H (t ) t
（2）
方程中的哈密顿量可以表示为
H H 0 H1
（3）
1
原子与光场的相互作用
H 0 和 H 1 分别为没有微扰和相互作用的哈密顿量， 利用它的完备性关系 a a b b 1 ，
我们可以把 H 0 表示为
H 0 =( a a b b ) H 0 ( a a b b )
wyp8514@
原子与光场的相互作用
第一章
两能级原子与光场相互作用的简单求解
原子的结构本身是非常复杂的， 一般是由一系列分立的能级组成， 且大部分能级是简并 的，为了研究原子与光场相互作用，我们将假设原子只有两个非简并的能级，让与光场相互 作用，我们通过不同的方法进行简单求解，得出相关性质与结论。
a b a =(
b b a b a ) E (t )
（5）
这里ab ba e a x b 是电偶极矩阵元， E (t ) 为原子场的，我们假设在电场中线 性偏振沿 x 轴线，我们可以把场表示为
E (t ) = cos vt
（6）
3.半经典方法求解
3.1 概率幅求解
对系统方程化简求解
a (t ) C b
C
（7）
a ab cos vt H ( cos vt b ba
求解将（7）和（8）代入薛定谔方程（2）可得
（8）
C a i a C a i R e i cos(vt)Cb Cb ib Cb i R e
= a a a b b b （4）
我们在利用了 H 0 a a a 和 H 0 b b b 之间的关系，而哈密顿量 H 1 在原子辐射 场中相互作用可以表示为
第三章-密度泛函理论3.3
3.3几种典型晶体的结合分散的原子相互结合成晶体的根本原因在于这些原子结合起来后整个系统具有更低的能量。
在结合过程中，有一定的能量W 释放出来，称为晶体的结合能。
如果以分散的原子作为计量相互作用势能的零点，则 -W 就是结合成晶体后系统的相互作用势能。
各种不同的晶体，其结合力的类型和大小是不同的。
但是在任何晶体中，两个原子之间的相互作用力或相互作用势与它们之间距离的关系在定性上是相同的。
晶体中原子的相互作用可以分为两大类，即吸引作用和排斥作用。
吸引作用是异性电荷之间的库仑引力，排斥作用是由于同性电荷之间的库仑斥力和泡利原理引起的排斥。
在某一适当的距离，两种力平衡，晶格处于稳定状态。
两个原子的相互作用势能通常可以用幂函数描述：()n m rBr A r u +-= (3.3.1)此处r 为两个原子之间的距离，A, B, m, n 皆为大于零的常数，第一项表示吸引能，第二项表示排斥能。
由势能u (r )可以计算相互作用力：()()drr du r f -= (3.3.2)图3.3.1 两个原子之间的相互作用力或相互作用势与它们之间距离的关系相互作用力为零时晶格最稳定，由此可以决定原子之间的平衡距离r 0：()00=⎪⎭⎫⎝⎛r dr r du (3.3.3)内能是晶体体积的函数，设开始原子相距很远，逐渐被压缩相互靠近，体积逐渐缩小，系统的相互作用势能U 逐渐下降，体积缩小到一定程度时，相互作用势能达到极小值。
这时如果再压缩系统，排斥的作用转变为主要的，相互作用势能将上升。
根据功能原理，系统温度不变时外界作功p (-dV )等于相互作用势能的增加dU ：dVdUp -= (3.3.4)在一般情况下，晶体受到的仅是大气压力p 0，由于数量级为大气压的压力对一般固体体积的影响很小，因此可以近似看作零。
由上式得：00≈=-p dVdU(3.3.5) 这个关系确定了平衡晶体的体积。
体积弹性模量的定义为：0V dV dp V B ⎪⎭⎫⎝⎛-= (3.3.6)其中p 为压力，V dV /-为相对体积变化。
两原子之间的相互作用叫做化学
两原子之间的相互作用叫做化学
化学是一门研究物质的组成、性质、结构、变化以及与能量的关系的科学学科。
化学中的一个重要概念是两个原子之间的相互作用，这种相互作用被称为化学键。
化学键是指原子之间的相互作用力，它们使得原子能够结合在一起形成分子或晶体。
化学键的形成涉及到原子中的电子，因为电子是决定原子化学性质的关键因素。
在化学中，常见的化学键包括共价键、离子键和金属键。
共价键是指两个原子通过共享电子对而相互结合。
这种键形成于非金属原子之间，如氧气中的氧分子（O2）。
离子键是指由正负电荷吸引而形成的键，其中一个原子失去电子而变成正离子，另一个原子获得电子而变成负离子。
金属键是指金属原子之间的一种特殊的键，其中金属原子通过电子云的共享而结合在一起。
化学键的强度取决于原子之间的相互作用力，这种相互作用力受到多种因素的影响，包括原子间的距离、电子的分布、原子核的电荷等。
不同类型的化学键在强度上有所不同，共价键通常比离子键强，而金属键通常是最强的。
化学键的形成和断裂是化学反应的基础。
通过改变原子之间的化学键，物质可以发生化学变化，形成新的物质。
化学反应可以是放热的（释放能量）或吸热的（吸收能量），这取决于化学键的形成和断裂过程中的能量变化。
总结来说，化学是研究物质组成、性质和变化的科学学科，其中两个原子之间的相互作用被称为化学键。
化学键的形成和断裂是化学反应的基础，通过改变化学键可以引起物质的化学变化。
不同类型的化学键具有不同的强度和特点，它们在物质的性质和行为中起着重要的作用。
原子交换作用范文
原子交换作用范文原子交换作用是一种重要的化学现象，它是指原子之间的电子交换，从而形成化学键。
原子交换作用对于物质的性质和反应起着重要的作用，对于理解化学反应机制和预测化学反应的速率和平衡也具有重要意义。
本文将从以下几个方面进行详细介绍。
1.原子交换作用的基本概念原子交换作用是指原子间电子的交换。
原子由原子核和绕核运动的电子组成，电子以电荷为基础，其负电荷趋向于正电荷，从而使原子保持稳定。
然而，当两个或多个原子靠近时，它们的电子云可能会重叠，从而产生电子的交换。
电子交换可能导致原子中电子的重新排列，从而形成新的化学键。
2.原子交换作用的类型离子交换是指电子从一个原子转移到另一个原子，从而形成正离子和负离子。
这种交换通常发生在具有不同电子亲和力或电离能的元素之间。
例如，钠原子可以失去一个电子并转变为正离子，氯原子可以接受这个电子并转变为负离子，从而形成氯化钠。
共价交换是指电子在两个原子之间共享，从而形成共价键。
这种交换通常发生在具有相似电子亲和力和电离能的元素之间。
例如，氢原子和氧原子共享电子，形成水分子，其中氢原子通过与氧原子共享一个电子对来稳定。
除了离子交换和共价交换，还存在一种特殊的交换作用，即金属键。
金属键是指金属原子之间的电子交换，形成金属晶格。
金属中的电子能够自由移动，形成电子云，从而使金属具有良好的电导性和热导性。
3.原子交换作用的影响首先，原子交换作用决定了物质的化学反应性质。
不同原子之间的交换方式不同，反应产物也会有所不同。
例如，钠和氯的离子交换会产生氯化钠，而氢和氧的共价交换会产生水。
原子交换作用还可解释为什么一些元素在化学反应中更具活性，而其他元素在化学反应中较不活跃。
其次，原子交换作用决定了物质的抗腐蚀性能。
具有高电子亲和力的金属原子容易进行电子交换，并形成具有抗腐蚀性的化合物。
例如，镀铬的钢材具有良好的抗腐蚀性能，是制造不锈钢的重要原料。
此外，原子交换作用还可以影响材料的导电性、热导性和光学性能等。
原子核的静电势能
原子核的静电势能1.引言1.1 概述概述部分的内容如下：引言是一篇文章的开端，旨在介绍文章的主题，概括性地解释文章的目的和结构，为读者提供一个对文章内容有基本了解的框架。
本文的主题是原子核的静电势能，通过探讨原子核静电势能的定义、原理以及影响因素，我们可以进一步理解原子核的性质和行为。
在本文的正文部分，我们将详细介绍原子核的静电势能的定义和原理，涵盖相关的基本概念和理论框架。
同时，我们还将探讨影响原子核静电势能的种种因素，包括核电荷、核半径和核壳效应等等。
在结论部分，我们将强调原子核静电势能的重要性，并探讨其可能的应用和未来进一步研究的方向。
通过本文的研究，我们可以深入了解并探讨原子核静电势能在核物理学中的重要作用。
掌握原子核的静电势能的概念和原理对于理解原子核的结构和稳定性具有重要意义。
此外，了解影响原子核静电势能的因素，能够帮助我们解释和预测核反应、放射性衰变等核现象。
原子核的静电势能也有可能在核能利用、医学及工业领域中找到实际应用。
为了更加深入地探索和利用原子核的静电势能，我们还需要进一步开展研究，以发现更多关于原子核性质和行为的有趣现象，并探索其在实际应用中的潜力。
通过本文的研究，我们旨在增进对原子核静电势能的理解，并为未来的研究和应用提供一定的参考。
通过对原子核的静电势能的探索，我们可以更加全面地认识原子核的性质和行为，为核物理学领域的发展做出贡献。
1.2文章结构1.2 文章结构本文将按以下结构进行叙述：第一部分为引言部分，对原子核的静电势能进行概述，并介绍文章的目的。
第二部分为正文部分，将首先对原子核的静电势能的定义和原理进行介绍，包括静电势能的起因和计算公式等内容。
其次，将探讨影响原子核静电势能的因素，如原子核的电荷分布、电子云的影响等。
通过对这些因素的分析，可以更好地理解和解释原子核的静电势能的形成机制。
第三部分为结论部分，将阐述原子核的静电势能的重要性，包括其在核物理学和相关领域中的应用以及对原子核结构和性质的影响。
原子互相吸引的原子力
原子互相吸引的原子力
原子互相吸引的原子力是一种基本的物理现象，它是构成物质的基础。
原子力是指原子之间的相互作用力，包括原子间的引力和斥力。
其中，原子间的引力是由于原子之间的电荷相互作用而产生的。
原子间的引力是一种非常强大的力量，它可以使得原子之间紧密地结
合在一起，形成分子和晶体。
在固体中，原子之间的引力非常强大，
因此固体具有很高的密度和硬度。
而在液体和气体中，原子之间的引
力比较弱，因此液体和气体具有较低的密度和流动性。
原子间的引力是由于原子之间的电荷相互作用而产生的。
原子中带有
正电荷的原子核和带有负电荷的电子互相吸引，形成了原子的结构。
当两个原子靠近时，它们之间的电子云会发生重叠，从而产生相互作
用力。
这种相互作用力可以是引力，也可以是斥力，具体取决于原子
之间的距离和电荷分布。
在原子间的引力中，范德华力是一种非常重要的力量。
范德华力是由
于原子之间的瞬时偶极子相互作用而产生的。
偶极子是指原子中电子
云的不对称性，它会导致原子产生瞬时的电荷分布不均。
当两个原子
靠近时，它们之间的瞬时偶极子会相互作用，从而产生范德华力。
范
德华力是一种非常弱的力量，但它在分子间相互作用中起着非常重要
的作用。
总之，原子间的引力是构成物质的基础，它决定了物质的性质和行为。
原子间的引力是由于原子之间的电荷相互作用而产生的，其中范德华
力是一种非常重要的力量。
了解原子间的引力对于理解物质的本质和
开发新材料具有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
像石墨结构内部层与层之间 的相互作用是一种较弱的作用力 。 这是物理作用力，属于分子作用 力。不属于化学键。
二、化学键的种类
（一）离子键 ——相邻的阴、阳离子存在强烈的静电作用。
钠原子最外层只有1个电子，很易失去它， 成为稳定结构。氯原子的最外层7个电子，较 易从别处获得1个电子，形成稳定结构。这样， 产生的钠离子和氯离子，阴阳离子达到引
思考：
卤素氢化物的稳定性是如何递变的呢？ 卤化氢 键能 KJ/mol 键长 nm HCl 432 0.127 HBr 366 0.141 HI 298 0.161 HF 568 0.092
稳定性： HF > HCl > HBr > HI
思考：
一百多种元素能组成世界上 3000多万种性能各异的物质，这种 情形与如下哪些因素有关？ (1)组成物质的元素种类各不相同 √ (2)所含的各种原子数目各不相同 √ (3)构成这些物质的原子在空间排 √ 列方式上各不相同 √ (4)连接原子的化学键种类各不相同 (5)化学键的键能大小各不相同 √
高 一
化 学
为什么100多种元 素能组成 3000 多万种 性能各异的物质呢？
3.1原子之间的相互作用
硬度高，熔点 相对于石墨低
柔软、润滑，熔点 相对于金刚石高
金刚石与石墨的结构
石墨滑动的结构示意
像金刚石、石墨中相邻的碳 原子之间存在强烈相互作用。我 们称之为化学键。 这种强烈作用是一种化学作 用力。这种力将邻近的原子紧密 结合在一起。
氯气的电子式
共价键
问题：共价键形成的条件是 什么？ 两个原子在电子的得失 能力相当之时结合，比较容 易形成共价键的形式。
如非金属原子之间的结合
共价键的形成或破坏，往往伴随着能量变化。
1.共价键的键能
1mol Cl (g) + 1mol Cl(g) → 1mol Cl2 (g) + 243 K J
力和斥力的平衡。最终形成了静电作用
力——离子键。
氯化钠固体中有许 多钠离子和氯离子构成
电子式：
思考： 还有哪些能形成离子键的物质？
活泼的金属元素和典型的非金属元素之 间的结合，往往容易形成离子键。
铵盐化合物也是离子化合物 能再列举一些实例吗？
原子之间的另一种结合方式：
（二）共价键 ——以共用电子对 的结合方式
对于氯化氢分子，共用电子对的电子为 氯原子和氢原子这两个原子所共有。对于氢 原子，其最外层就达到2个电子稳定结构， 对于氯原子，其最外层就达到8个电子稳定 结构。
氯化氢的电子式：
氢分子中的氢原子是怎样结合的呢？
以共用电子对形式结合，共价键
氢分子电子式：
H∶H
思考：氯分子为什么是以双原子分子 形式存在，而不是以单原子分子？两 个氯原子之间的结合是以什么化学键 呢？
（三） 金属键
以金属阳离子和自由电子之间的强烈作用。
小结：
1. 什么是化学键？ 相邻原子之间强烈的作用。
2.化学键的主要类型有哪些？
离子键、共价键和金属键 3.什么是离子键、共价键？试举例。 4.共价键的牢固程度与键能成正比， 与键长成反比。 5.分子作用力比较弱，不属于化学键
判断正误 1.离子键就是化合物中的相邻的阴、 √ 阳离子之间的静电作用。 2.离子键一定是存在于化合物中。 √ 3.共价键一定存在于化合物中。 × 4.某些化合物可以同时具有离子键 √ 和共价键。 5.某些化合物同时具有离子键和共 × 价键，既可以称之为离子化合物， 也可称之为共价化合物。
243 K J，这就是1mol Cl—Cl共价键的键能。
生成共价键会放出能量，反之，破坏共价键就需 要吸收能量。 键能数值越大，代表共价键越强、越牢固。
2.共价键的键长
键长越长，往往共价键越弱。
硬度高
熔点略低
柔软润滑， 金属的原子之间是以什么形式结合的呢？