第三章 系统时间响应习题及解答
第三章习题

第三章 复习题一、是非题1 传递函数完整地描述了系统的动态特性2 两个元件串联的传递函数就等于单个元件传递函数之积3 引入积分环节就能消除稳态误差4 系统中是否存在稳态误差取决于a) 系统的结构参数b) 外作用的形式(阶跃,斜坡……)5 多输入,多输出系统,当输出输入信号变化时,系统极点会相应改变。
6 闭环系统的稳定性总比开环系统好。
1. 典型欠阻尼二阶系统超调量大于5%,则其阻尼ξ的范围为:(1) ξ>1 (2) 0<ξ<1 (3) 1>ξ>0.707 (4) 0<ξ<0.7072. 二阶系统的闭环增益加大(1) 快速性能好 (2)超调量愈大(3)p t 提前(4)对动态特性无影响3. 欠阻尼二阶系统,n ξω两者都与(1)%σ有关 (2) %σ无关 (3) p t 有关 (4) p t 无关4. 一阶系统的闭环极点越靠近s 平面的原点,其(1)响应速度越慢 (2)响应速度越快 (3)准确度越高 (4)准确度越低5. 系统时间响应的瞬态分量(1)是某一瞬时的输出值 (2)反映系统的准确度(3)反映系统的动特性 (4)只取决于闭环极点6. 典型欠阻尼二阶系统中再加入一个闭环零点,则(1)对动态性能无影响 (2) %σ↓ (3) %σ↑ (4) p t ↑7. 欠阻尼典型二阶系统若n ω不变,ξ变化时(1) 当0.707ξ>时,s t ξ↑→↓ (2) 当0.707ξ>时,s t ξ↑→↑(3) 当0.707ξ<时,s t ξ↑→↓ (4) 当0.707ξ<时,s t ξ↑→不变8. 单位反馈系统,闭环传递函数为11Ts +,()r t t =时,系统稳态误差ss e = (1) ∞ (2) T (3)1T(4)0 9. 已知某系统的型别为v ,输入为()n r t t =(n 为正整数),则系统稳态误差为零的条件是(1)v n ≥ (2)v n > (3) v n ≤ (4)v n < 10. I 型单位反馈系统的闭环增益为(1)与开环增益有关 (2) 与()r t 形式有关(3) 1 (4)与各环节时间常数有关11. 系统闭环零点影响系统的(1) 稳定性 (2)稳态误差 (3)调节时间 (4)超调量1.已知系统结构图如右所示:其单位阶跃响应的超调量%16.3%σ=,峰值时间1p t =秒求 1)开环传递函数()?G s =2)闭环传递函数()?s Φ=3)根据性能指标%,p t σ,确定参数K 及τ4)计算等速输入(恒速值 1.5A =度/秒)时系统的稳态误差值 解:[]111010(1)(1)().;10(110)1(1)K s s G s K s s s s ττ+==++++开环增益110110K K τ=+ 21222110()(2)() (*)1()(110)102n n nK G s s G s s s K s s ωτξωωΦ===++++++ ⑶依题:%16.3%0.5σξ=→=1 3.6276 (**)p n t ω==→===2211(**)(*) 10 3.6276213.159 1.3159n K K ω→===→=2120.5 3.62761 21100.2631010n n ξωξωττ-⨯⨯-=+→=== 111.31591013.159 3.6250.263110 2.631K K K ττ=⎧∴⇒===⎨=++⎩ 1.5(4)0.4143.625ss A e K ===2系统如下图示)(1)(t t r 时的响应为)(t h求a K K ,,21解:依题可知⎪⎪⎩⎪⎪⎨⎧=-===∞%92218.2%''75.02)(σp t h )1( 22)(2222212221⎪⎩⎪⎨⎧==⇒++=++=Φnn n n n a K s s K K as s K K s ξωωωξωω )2( 21..lim )().(.lim )(1222100==++=Φ=∞→→K sK as s K K s s R s s h s s )4( 75.012=-=n p t ωξπln 0.090.7665%0.09 (5)0.60833(52.55)e πσξβ-=-===⎪===︒⎪⎩:)4()5(→(6) 236.5608.0175.02秒弧=-=πωn)1()6).(5(→⎪⎩⎪⎨⎧==⨯⨯=====237.6236.5608.0224.27236.51222K a K n n ξωω系统极点分布:⎩⎨⎧=︒==236.55.52arccos nωξβ3 如图所示,参考输入r(t)=a ∙t (t), 干扰n(t)=b (t). 求系统总的稳态误差。
自动控制原理第三章习题解答

tp =
1−ξ 2
= e −π 0.6 /
1−0.62
= e −π 0.6 /
1−0.62
= 9 .5 %
π
1 − ξ ωn
2
=
π
1.6
= 1.96( s )
ts =
3-5
3.5
ξω n
=
3.5 = 2.92( s ) 1.2
设单位反馈系统的开环传递函数为
G ( s) =
0.4 s + 1 s ( s + 0.6)
s5 s4 s3 s2 s1 s0
1 12 35 3 20 25 16 80 3 3 5 25 10 25
有一对虚根,系统不稳定 3-13 已知单位反馈系统的开环传递函数
G ( s) =
K (0.5s + 1) s ( s + 1)(0.5s 2 + s + 1)
试确定系统稳定时的 K 值范围。 解:系统特征方程为
ε 0 ,试问 k1 应满足什么条件?
见习题 3-20 解答 3-2 设系统的微分方程式如下: (1)
&(t ) = 2r (t ) 0.2c
&&(t ) + 0.24c &(t ) + c(t ) = r (t ) (2) 0.04c
试求系统的单位脉冲响应 k(t)和单位阶跃响应 h(t)。已知全部初始条件为零。 解: (1) 因为 0.2 sC ( s ) = 2 R ( s ) 单位脉冲响应: C ( s ) = 10 / s 单位阶跃响应 h(t)
试求系统的超调量σ%、峰值时间tp 和调节时间ts。 解: h(t ) = 1 −
自动控制原理第三章课后习题答案(最新)汇总

3-1设系统的微分方程式如下:(1)0.2c(t) 2r(t)单位脉冲响应:C(s) 10/s g(t) 103t3 3tc(t) 1 e cos4t e si n4t413-2 温度计的传递函数为 —,用其测量容器内的水温,1min 才能显示出该温度的Ts 198%的数值。
若加热容器使水温按 10(C/min 的速度匀速上升,问温度计的稳态指示误差有多大?解法一 依题意,温度计闭环传递函数由一阶系统阶跃响应特性可知: c(4T) 98 o o ,因此有 4T 1 min ,得出T 0.25 min 。
视温度计为单位反馈系统,则开环传递函数为(s)1K 1TG(s)—1(s) Tsv 1用静态误差系数法,当r(t) 10t 时,e ss10 10T 2.5 C oK(2) 0.04c(t)0.24c(t) c(t)r(t)试求系统闭环传递函数① 部初始条件为零。
解:(s),以及系统的单位脉冲响应 g(t)和单位阶跃响应 c(t)。
已知全(1)因为 0.2sC(s)2R(s) 闭环传递函数(s)C(s) 10R(s) s单位阶跃响应c(t) C(s) 10/s 2c(t) 10t t 0(2) (0.04s 20.24s 1)C(s) R(s)C (s )闭环传递函数(s)C(s) R(s)120.04s0.24s 1单位脉冲响应:C(s)120.04s 2 0.24s 1g(t)25 e 33tsi n4t单位阶跃响应h(t) C(s)25 s[(s 3)216]1 s 6 s (s 3)216(s)1 Ts 1解法二依题意,系统误差疋义为e(t) r(t) c(t),应有e(s)E(s)1 C(s)R(s)11 TsR(s) Ts 1 Ts 13-3 已知二阶系统的单位阶跃响应为c(t) 10 12.5e 1.2t sin(1.6t 53.1o)试求系统的超调量c%、峰值时间t p和调节时间t'si n( 1n t )t p Jl- 1.96(s■1 2n1.63.5 3.5t s 2.92(s)n 1.2或:先根据c(t)求出系统传函,再得到特征参数,带入公式求解指标。
第三章 线性系统的时域分析与校正 习题及答案

第三章 线性系统的时域分析与校正习题及答案3-1 已知系统脉冲响应t e t k 25.10125.0)(-=试求系统闭环传递函数)(s Φ。
解 Φ()()./(.)s L k t s ==+00125125 3-2 设某高阶系统可用下列一阶微分方程T c t c t r t r t ∙∙+=+()()()()τ近似描述,其中,1)(0<-<τT 。
试证系统的动态性能指标为 T T T t d ⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-+=τln 693.0t T r =22. T T T t s ⎥⎦⎤⎢⎣⎡-+=)ln(3τ 解 设单位阶跃输入ss R 1)(=当初始条件为0时有:11)()(++=Ts s s R s C τ 11111)(+--=⋅++=∴Ts T s s Ts s s C ττC t h t T Te t T()()/==---1τ 1) 当 t t d = 时h t T Te t td ()./==---051τ12=--T T e t T d τ/ ; T t T T d -⎪⎭⎫ ⎝⎛-=-τln 2ln ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=∴T T T t d τln 2ln2) 求t r (即)(t c 从1.0到9.0所需时间)当 Tt e TT t h /219.0)(---==τ; t T T T 201=--[ln()ln .]τ 当 Tt e TT t h /111.0)(---==τ; t T T T 109=--[ln()ln .]τ 则 t t t T T r =-==21090122ln ... 3) 求 t sTt s s e TT t h /195.0)(---==τ ]ln 3[]20ln [ln ]05.0ln [ln TT T T T T T T T t s τττ-+=+-=--=∴3-3 一阶系统结构图如图3-45所示。
要求系统闭环增益2=ΦK ,调节时间4.0≤s t s ,试确定参数21,K K 的值。
自动控制原理第3章练习题

第三章 线性系统的时域分析习题及答案3-1 已知系统脉冲响应t e t k 25.10125.0)(-=试求系统闭环传递函数)(s Φ。
解: Φ()()./(.)s L k t s ==+001251253-2 设某高阶系统可用下列一阶微分方程T c t c t r t r t ∙∙+=+()()()()τ近似描述,其中,1)(0<-<τT 。
试证系统的动态性能指标为t T r =22.T T T t s ⎥⎦⎤⎢⎣⎡-+=)ln(3τ 解: 设单位阶跃输入ss R 1)(=当初始条件为0时有:11)()(++=Ts s s R s C τ 11111)(+--=⋅++=∴Ts T s s Ts s s C ττC t h t T Te t T()()/==---1τ 1) 求t r (即)(t c 从1.0到9.0所需时间)当 Tt e TT t h /219.0)(---==τ; t T T T 201=--[ln()ln .]τ 当 Tt e TT t h /111.0)(---==τ; t T T T 109=--[ln()ln .]τ 则 t t t T T r =-==21090122ln ...2) 求 t sTt s s e TT t h /195.0)(---==τ ]ln 3[]20ln [ln ]05.0ln [lnTT T T T T T T T t s τττ-+=+-=--=∴3-3 一阶系统结构图如图3-45所示。
要求系统闭环增益2=ΦK ,调节时间4.0≤s t s ,试确定参数21,K K 的值。
解: 由结构图写出闭环系统传递函数111)(212211211+=+=+=ΦK K sK K K s K s K K s K s令闭环增益212==ΦK K , 得:5.02=K 令调节时间4.03321≤==K K T t s ,得:151≥K 。
3-4在许多化学过程中,反应槽内的温度要保持恒定, 图3-46(a )和(b )分别为开环和闭环温度控制系统结构图,两种系统正常的K 值为1。
信号与系统课后习题与解答第三章
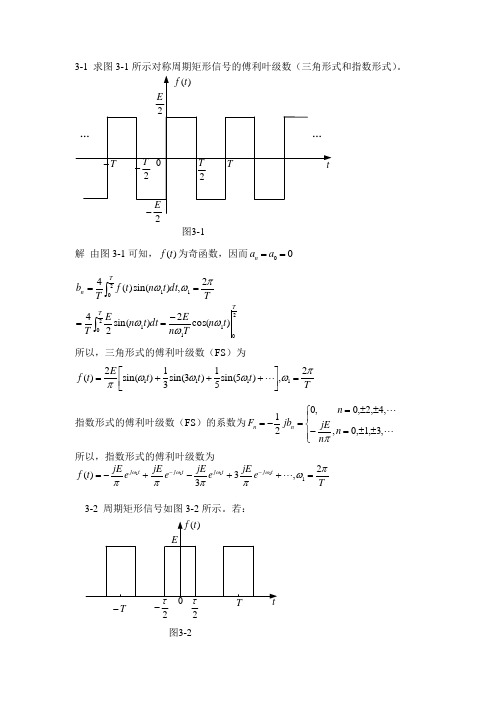
3-1 求图3-1所示对称周期矩形信号的傅利叶级数(三角形式和指数形式)。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数(FS )为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数(FS )的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
若:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数(FS )的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数(FS )为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:(1))(1t f 的谱线间隔和带宽(第一零点位置),频率单位以kHz 表示; (2))(2t f 的谱线间隔和带宽; (3))(1t f 与)(2t f 的基波幅度之比; (4))(1t f 基波与)(2t f 三次谐波幅度之比。
自动控制原理第三章习题答案

第三章习题答案名词解释1.超调量:系统响应的最大值与稳态值之差除以稳态值。
定义为)()(max ∞∞-=c c c σ 2.开环传递函数中含有2个积分因子的系统称为II 型系统。
3.单位阶跃响应达到第一个峰值所需时间。
4.指响应达到并保持在终值5%内所需要的最短时间。
5. 稳态误差:反馈系统误差信号e(t) 的稳态分量(1分),记作e ss (t)。
6.开环传递函数中不含有积分因子的系统。
7.上升时间:○1响应从终值10%上升到终值90%所需的时间;或○2响应从零第一次上升到终值所需的时间。
简答1. 在实际控制系统中,总存在干扰信号。
1) 时域分析:干扰信号变化速率快,而微分器是对输入信号进行求导,因此干扰信号通过微分器之后,会产生较大的输出;2) 频域分析:干扰信号为高频信号,微分器具有较高的高频增益,因此干扰信号易被放大。
这就是实际控制系统中较少使用纯微分器的原因。
2.系统稳定的充分条件为:劳斯阵列第一列所有元素不变号。
若变号,则改变次数代表正实部特征根的数目。
3.二阶临界阻尼系统特征根在负实轴上有两个相等的实根,其单位阶跃响应为单调递增曲线,最后收敛到一个稳态值。
4. 闭环特征根严格位于s 左半平面;或具有负实部的闭环特征根。
5.欠阻尼状态下特征根为一对具有负实部的共轭复数,单位阶跃响应是一个振荡衰减的曲线,最后收敛到一个稳态值。
6.阻尼小于-1的系统,特征根位于正实轴上,单位阶跃响应是一个单调发散的曲线。
7. 无阻尼状态下特征根为一对虚根,响应为等幅振荡过程,永不衰减。
8.图4(a)所示系统稳定,而图4(b)所示系统不稳定。
原因是图4(b)所示系统的小球收到干扰后将不能恢复到原来的平衡状态。
9.不能。
原因是:两个一阶惯性环节串联后的极点为实极点;而二阶振荡环节的极点为复数极点。
计算题1. 解:r(t)=2t.v=1,系统为I 型系统k v =2,e ss =1.2.解:构造Routh 表:25:010:255:03/803/16:25203:35121:012345s s s s s s辅助方程:02552=+s 故纯虚根为:j s 52,1±=;故系统处于临界稳定状态。
自动控制原理第3章 习题及解析

自动控制原理(上)习 题3-1 设系统的结构如图3-51所示,试分析参数b 对单位阶跃响应过渡过程的影响。
考察一阶系统未知参数对系统动态响应的影响。
解 由系统的方框图可得系统闭环响应传递函数为/(1)()()111K Ts Ks Kbs T Kb s Ts +Φ==++++ 根据输入信号写出输出函数表达式:111()()()()()11/()K Y s s R s K s T Kb s s s T bK =Φ⋅=⋅=-++++对上式进行拉式反变换有1()(1)t T bKy t K e-+=-当0b >时,系统响应速度变慢;当/0T K b -<<时,系统响应速度变快。
3-2 设用11Ts +描述温度计特性。
现用温度计测量盛在容器内的水温,发现1min 可指示96%的实际水温值。
如果容器水温以0.1/min C ︒的速度呈线性变化,试计算温度计的稳态指示误差。
考察一阶系统的稳态性能分析(I 型系统的,斜坡响应稳态误差)解 由开环传递函数推导出闭环传递函数,进一步得到时间响应函数为:()1t T r y t T e -⎛⎫=- ⎪⎝⎭其中r T 为假设的实际水温,由题意得到:600.961Te-=-推出18.64T =,此时求输入为()0.1r t t =⋅时的稳态误差。
由一阶系统时间响应分析可知,单位斜坡响应的稳态误差为T ,所以稳态指示误差为:lim ()0.1 1.864t e t T →∞==3-3 已知一阶系统的传递函数()10/(0.21)G s s =+今欲采用图3-52所示负反馈的办法将过渡过程时间s t 减小为原来的1/10,并保证总的放大倍数不变,试选择H K 和0K 的值。
解 一阶系统的调节时间s t 与时间常数成正比,则根据要求可知总的传递函数为10()(0.2/101)s s Φ=+由图可知系统的闭环传递函数为000(10()()1()0.211010110()0.21110H HHHK G s K Y s R s K G s s K K K s s K ==++++==Φ++)比较系数有101011011010HHK K K ⎧=⎪+⎨⎪+=⎩ 解得00.9,10H K K ==3-4 已知二阶系统的单位阶跃响应为1.5()1012sin(1.6+53.1t y t e t -=-)试求系统的超调量%σ,峰值时间p t ,上升时间r t 和调节时间s t 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 线性系统的时域分析与校正习题及答案3-3 一阶系统结构图如图所示。
要求系统闭环增益2=ΦK ,调节时间4.0≤s t s ,试确定参数21,K K 的值。
解 由结构图写出闭环系统传递函数111)(212211211+=+=+=ΦK K sK K K s K sK K s K s令闭环增益212==ΦK K , 得:5.02=K 令调节时间4.03321≤==K K T t s ,得:151≥K 。
3-2 单位反馈系统的开环传递函数)5(4)(+=s s s G ,求单位阶跃响应)(t h 和调节时间t s 。
解:依题,系统闭环传递函数)1)(1(4)4)(1(4454)(212T s T s s s s s s ++=++=++=Φ ⎩⎨⎧==25.0121T T41)4)(1(4)()()(210++++=++=Φ=s C s C s C s s s s R s s C1)4)(1(4lim)()(lim 000=++=Φ=→→s s s R s s C s s34)4(4lim)()()1(lim 011-=+=Φ+=→-→s s s R s s C s s31)1(4lim)()()4(lim 042=+=Φ+=→-→s s s R s s C s st t e e t h 431341)(--+-=421=T T , ∴3.33.3111==⎪⎪⎭⎫ ⎝⎛=T T T t t s s 。
159.075.40''<''==T t s3-3 机器人控制系统结构图如图所示。
试确定参数21,K K 值,使系统阶跃响应的峰值时间5.0=p t s ,超调量%2%=σ。
解 依题,系统传递函数为222121212112)1()1()1(1)1()(n n n s s K K s K K s K s s s K K s s K s ωξωωΦΦ++=+++=++++= 由 ⎪⎩⎪⎨⎧=-=≤=--5.0102.0212np oo t e ωξπσξπξ 联立求解得⎩⎨⎧==1078.0n ωξ 比较)(s Φ分母系数得⎪⎩⎪⎨⎧=-===146.0121001221K K K n n ξωω 3-4 某典型二阶系统的单位阶跃响应如图所示。
试确定系统的闭环传递函数。
解 依题,系统闭环传递函数形式应为2222.)(nn ns s K s ωξωω++=ΦΦ 由阶跃响应曲线有:21)(lim )()(lim (0==⋅Φ=Φ=∞Φ→→K ss s s R s s h s s ) ⎪⎪⎩⎪⎪⎨⎧=-===-=--o oo o n p e t 25225.221212ξξπσξωπ联立求解得 ⎩⎨⎧==717.1404.0n ωξ所以有 95.239.19.5717.1717.1404.02717.12)(2222++=+⨯⨯+⨯=Φs s s s s 3-5 设图(a )所示系统的单位阶跃响应如图(b )所示。
试确定系统参数,1K 2K 和a 。
解 由系统阶跃响应曲线有⎪⎩⎪⎨⎧=-===∞oo o op t h 3.333)34(1.03)(σ系统闭环传递函数为222212212)(nn n s s K K as s K K s ωξωω++=++=Φ (1)由 ⎪⎩⎪⎨⎧===-=--o o o o np et 3.331.01212ξξπσωξπ 联立求解得 ⎩⎨⎧==28.3333.0n ωξ 由式(1)⎩⎨⎧====222110821n n a K ξωω另外 3lim 1)(lim )(2122100==++=⋅Φ=∞→→K K as s K K s s s h s s 5.21)(lim )(0=⋅Φ=∞→ss s h s 3-6 已知系统的特征方程,试判别系统的稳定性,并确定在右半s 平面根的个数及纯虚根。
(1)01011422)(2345=+++++=s s s s s s D (2)0483224123)(2345=+++++=s s s s s s D (3)022)(45=--+=s s s s D(4)0502548242)(2345=--+++=s s s s s s D解(1)1011422)(2345+++++=s s s s s s D =0Routh : S 5 1 2 11 S 4 2 4 10 S 3 ε 6 S 2εε124- 10S 6 S 0 10第一列元素变号两次,有2个正根。
(2)483224123)(2345+++++=s s s s s s D =0 Routh : S 5 1 12 32S 4 3 24 48 S 33122434⨯-= 32348316⨯-= 0S 2424316412⨯-⨯= 48S 1216448120⨯-⨯= 0 辅助方程 124802s +=,S 24 辅助方程求导:024=sS 0 48系统没有正根。
对辅助方程求解,得到系统一对虚根 s j 122,=±。
(3)022)(45=--+=s s s s DRouth : S 5 1 0 -1S 4 2 0 -2 辅助方程 0224=-sS 3 8 0 辅助方程求导 083=sS 2 ε -2 S ε16S 0 -2第一列元素变号一次,有1个正根;由辅助方程0224=-s 可解出: ))()(1)(1(2224j s j s s s s -+-+=-))()(1)(1)(2(22)(45j s j s s s s s s s s D -+-++=--+= (4)0502548242)(2345=--+++=s s s s s s D Routh : S 5 1 24 -25S 4 2 48 -50 辅助方程 05048224=-+s sS 3 8 96 辅助方程求导 09683=+s sS 2 24 -50 S 338/3S 0 -50第一列元素变号一次,有1个正根;由辅助方程05048224=-+s s 可解出: )5)(5)(1)(1(25048224j s j s s s s s -+-+=-+)5)(5)(1)(1)(2(502548242)(2345j s j s s s s s s s s s s D -+-++=--+++=3-7 单位反馈系统的开环传递函数为)5)(3()(++=s s s Ks G要求系统特征根的实部不大于1-,试确定开环增益的取值范围。
解 系统开环增益 15K K k =。
特征方程为: 0158)(23=+++=K s s s s D 做代换 1-'=s s 有:0)8(25)1(15)1(8)1()(2323=-+'+'+'=+-'+-+-'='K s s s K s s s s DRouth : S 3 1 2 S 2 5 K-8 S 518K - 18<⇒KS 0 8-K 8>⇒K使系统稳定的开环增益范围为:151815158<=<K K k 。
3-8 温度计的传递函数为11+Ts ,用其测量容器内的水温,1min 才能显示出该温度的98%的数值。
若加热容器使水温按10ºC/min 的速度匀速上升,问温度计的稳态指示误差有多大?解法一 依题意,温度计闭环传递函数11)(+=ΦTs s 由一阶系统阶跃响应特性可知:o o T h 98)4(=,因此有 min 14=T ,得出 min 25.0=T 。
视温度计为单位反馈系统,则开环传递函数为Tss s s G 1)(1)()(=Φ-Φ=⎩⎨⎧==11v TK 用静态误差系数法,当t t r ⋅=10)( 时,C T Ke ss ︒===5.21010。
解法二 依题意,系统误差定义为 )()()(t c t r t e -=,应有 1111)()(1)()()(+=+-=-==ΦTs TsTs s R s C s R s E s e C T sTs Ts ss R s s e s e s ss ︒==⋅+=Φ=→→5.210101lim )()(lim 203-9 系统结构图如图所示。
试求局部反馈加入前、后系统的静态位置误差系数、静态速度误差系数和静态加速度误差系数。
解 局部反馈加入前,系统开环传递函数为 )1()12(10)(2++=s s s s G∞==∞→)(lim s G K s p∞==→)(lim 0s sG K s v10)(lim 20==→s G s K s a局部反馈加入后,系统开环传递函数为)20()12(1012011(1012)(2+++=+++⋅+=s s s s s s s s s s G )()∞==→)(lim 0s G K s p5.0)(lim 0==→s sG K s v0)(lim 20==→s G s K s a3-10 单位反馈系统的开环传递函数为)5(25)(+=s s s G(1) 求各静态误差系数和25.021)(t t t r ++=时的稳态误差ss e ; (2) 当输入作用10s 时的动态误差是多少?解 (1))5(25)(+=s s s G ⎩⎨⎧==15v K∞=+==→→)5(25lim)(lim 0s s s G K s s p5525lim)(lim 0=+==→→s s G s K s s v0525lim)(lim 020=+==→→s ss G s K s s a )(1)(1t t r =时, 0111=+=pss K et t r 2)(2=时, 4.0522===v ss K A e 235.0)(t t r =时,∞===13a ss K A e 由叠加原理 ∞=++=321ss ss ss ss e e e e (2) 题意有255)5()(11)(2+++=+=Φs s s s s G s e用长除法可得 ++=++++=Φ3332210008.02.0)(s s s C s C s C C s e008.002.003210====C C C C)(1)(2)(5.021)(2='''=''+='++=t r t r tt r t t t r∴ t t r C t r C t r C t r C t e s 2.04.0)()()()()(3210+=+'''+''+'+=∴ 4.2)10(=s e3-11 控制系统结构图如图所示。
其中1K ,02>K ,0≥β。
试分析: (1)β值变化(增大)对系统稳定性的影响;(2)β值变化(增大)对动态性能(%σ,s t )的影响; (3)β值变化(增大)对t a t r =)(作用下稳态误差的影响。
