电路分析答案解析第五章
电路分析智慧树知到课后章节答案2023年下上海电力大学

电路分析智慧树知到课后章节答案2023年下上海电力大学上海电力大学第一章测试1.图示电路中,节点A和B之间的电压UAB为()V。
A:19 B:16 C:-16 D:21答案:-162.图示电路中I= 0 时,电位UA=()V。
A:70 B:90 C:-10 D:60答案:603.通常所说负载增加,是指负载()增加。
A:电阻 B:功率 C:电流 D:电压答案:功率4.图示电路中S断开时I1= 0A,I=2A。
S闭合时I1=( )A,I=( )A。
()A:3 B:0 C:6 D:2答案:0;65.图示电路中,当IS=10A 时,电压U为()V,当IS=8A时电压U为()V。
()A:0 B:16 C:12 D:8答案:16;126.电路理论分析的对象是电路模型而不是实际电路。
()A:错 B:对答案:对7.欧姆定律可表示成U=RI,也可表示成U=-RI,这与采用的参考方向有关。
()A:对 B:错答案:对8.在节点处各支路电流的方向不能均设为流向节点,否则将只有流入节点的电流而无流出节点的电流。
()A:错 B:对答案:错9.在电压近似不变的供电系统中,负载增加相当于负载电阻减少。
()A:错 B:对答案:对10.理想电压源的端电压是由它本身确定的,与外电路无关,因此流过它的电流则是一定的,也与外电路无关。
()A:对 B:错答案:错第二章测试1.图示电路AB间的等效电阻为()。
A:24Ω B:14Ω C:12Ω D:10.67Ω答案:14Ω2.电路如图所示,A、B端的等效电阻R=()。
A:5Ω B:4Ω C:10Ω D:20Ω答案:4Ω3.电路如图所示,可化简为()A:不能化简B:8Ω电阻C:13Ω电阻D:3Ω电阻答案:3Ω电阻4.如图所示电路中,当电阻R2增加时电流I将()。
A:不变 B:增加 C:减小答案:增加5.图示电路中,就其外特性而言,()。
A:a、d等效 B:a、b、c、d均等效 C:a、b等效 D:b、c等效答案:b、c等效6.两只额定电压为110V的电灯泡串联起来总可以接到220V的电压源上使用。
电路分析第5章 三相电路

A Z N B C 星形接法
返 回
A Z Z B C
•
Z
Z
•
Z
•
三角形接法
上一页 下一页
第5章 三相电路 章
一、三相四线制星形接法
A N C B
+
uA
-
iA iN
|ZA|
uB +
N′
所以
根据对称关系, 根据对称关系,其它两相电流为
= 22 2 sin(ω t − 173°) A
= 22 2 sin(ω t + 67°) A
返 回
上一页
下一页
第5章 三相电路 章
(2)负载不对称时,各相单独计算。 (2)负载不对称时,各相单独计算。 负载不对称时 相电压为Up=220V的对称电源;各相负载为电 的对称电源; 例4.2.2-4.2.4 相电压为 的对称电源 灯组,在额定220V电压下各相电阻分别为 A=5 , RB=10 , 电压下各相电阻分别为R 灯组,在额定 电压下各相电阻分别为 RC=20 。试求下列各种情况下的负载相电压、负载电流及 试求下列各种情况下的负载相电压、 中性线电流。(1) 如上所述,正常状态下; (2) A相短路时; 中性线电流。 ) 如上所述,正常状态下; ) 相短路时; 相短路时 相短路, 相断开时; (3) A相短路,中性线又断开时; (4) A相断开时; (5) A ) 相短路 中性线又断开时; ) 相断开时 ) 相断开,中性线又断开时。 相断开,中性线又断开时。 解: 1)正常状态 ( ) 虽然负载不对称,因中性 虽然负载不对称,因中性线 的存在, 的存在,负载相电压与电源 C 的相电压相等也是对称的, 的相电压相等也是对称的, 有效值亦为 220V。 。
第5章课后习题参考答案

第五章组合逻辑电路1.写出如图所示电路的输出信号逻辑表达式,并说明其功能。
(a)(b)解:(a)Y1ABC(判奇功能:1的个数为奇数时输出为1)Y2AB(AB)CABACBC(多数通过功能:输出与输入多数一致)(b)Y1(AB)A(AB)BABAB(同或功能:相同为1,否则为0)2.分析如图所示电路的逻辑功能(a)(b)(c)解:(a)Y1ABAB(判奇电路:1的个数为奇数时输出为1)0011(b)Y2(((AA)A)A)(判奇电路:1的个数为奇数时输出为1)0123YAM00(c)Y1 A M1(M=0时,源码输出;M=1时,反码输出)YAM233.用与非门设计实现下列功能的组合逻辑电路。
(1)实现4变量一致电路。
(2)四变量的多数表决电路解:(1)1)定变量列真值表:ABCDYABCDY0000110000000101001000100101000011010110010*******010*******011001110001110111112)列函数表达式:YABCDABC D ABCDABCD3)用与非门组电路(2)输入变量A、B、C、D,有3个或3个以上为1时输出为1,输人为其他状态时输出为0。
1)列真值表2)些表达式3)用与非门组电路4.有一水箱由大、小两台水泵ML和Ms供水,如图所示。
水箱中设置了3个水位检测元件A、B、C,如图(a)所示。
水面低于检测元件时,检测元件给出高电平;水面高于检测元件时,检测元件给出低电平。
现要求当水位超过C点时水泵停止工作;水位低于C点而高于B点时Ms单独工作;水位低于B点而高于A点时ML单独工作;水位低于A点时ML和Ms同时工作。
试用门电路设计一个控制两台水泵的逻辑电路,要求电路尽量简单。
解:(1)根据要求列真值表(b)(b)(a)(2)真值表中×对应的输入项为约束项,利用卡诺图化简(c)(d)(c)(d)(e)得:MABCsMBL(ML、M S的1状态表示工作,0状态表示停止)(3)画逻辑图(e)5.某医院有—、二、三、四号病室4间,每室设有呼叫按钮,同时在护士值班室内对应地装有一号、二号、三号、四号4个指示灯。
电路分析 张永瑞 王松林 答案

uL (t)
=
L
diL (t) dt
=
−20e−5t
A
5.14 如题 5.14 图所示电路,t < 0 已处于稳态,当 t = 0 时开关 S 闭合,求 t ≥ 0
时的电流 i(t) 。 解:在 t ≥ 0 ,开关闭合,根据电路的
特殊性,电流 i(t) 可以看成电压源和电容 初始储能作用的叠加。可利用三要素公式 进行求解:
iC
(t )
=
C
duC (t) dt
=
1.2e−2t
A
u(t) = uC (t) + iC (t)R = 6(1− e−2t ) + 4.8e−2t = (6 −1.2e−2t )V
4Ω
iC +
0.1F
uC
-
5.9 如题 5.9 图所示电路,t < 0 时已处于稳态。当 t = 0 时开关 S 闭合,求 t ≥ 0
零状态响应方程为:
duC (t) dt
+
2uC
(t)
=
12
uC (0+ ) = 0
其齐次为:
Ke−2t
4
其特解为:
A0 代入方程有: 2 A0 = 12
通解为:
uCzs (t) = Ke−2t + 6
代入初始条件: 0 = K + 6 K = −6
得:
uCzs (t) = 6(1− e−2t )V
+ 25V 1F -
S +
uC 5Ω
-
5.13 如题 5.13 图所示电路,t < 0 已处于稳态,当 t = 0 时开关 S 打开,求 t ≥ 0
电路分析基础第四版课后习题答案
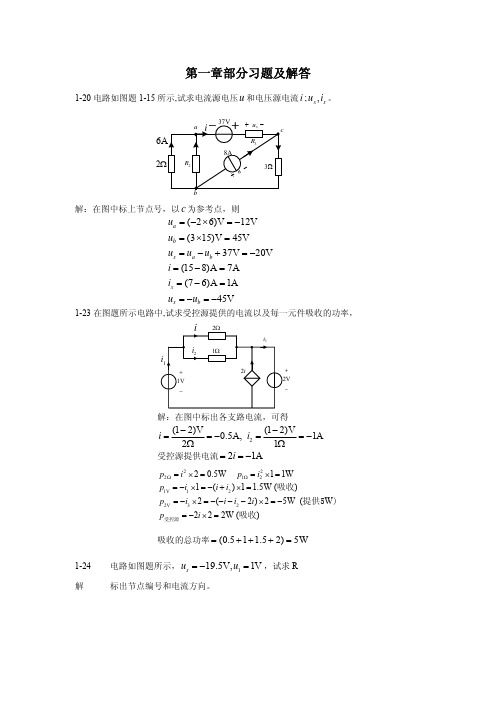
i
i1
+ 1V −
2Ω
i3
i2
1Ω
2i
+ 2V −
解:在图中标出各支路电流,可得
(1 − 2)V (1 − 2)V = −0.5A, i2 = = −1A 2Ω 1Ω 受控源提供电流 = 2i = −1A i=
p2 Ω = i 2 × 2 = 0.5W
为确定 R,需计算 i4 ,
uce = ucd + ude = 0 ⇒ ude = −ucd = −10u1 = −10V
故
i3 =
udc = −2.5A, i4 = is − i3 = (−3.5 + 2.5)A = −1A 4 R = 0Ω 由此判定
1-33
试用支路电流法求解图题所示电路中的支路电流 i1 , i2 , i3 。
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2
⎧25i1 − 20i2 − 5i3 = 50 ⎪ 代入并整理得: ⎨−5i1 + 9i2 − 4i3 = 0 解得 ⎪−5i − 4i + 10i = 0 2 3 ⎩ 1
受控源电压 受控源功率
⎧i1 = 29.6A ⎨ ⎩i2 = 28A
i2
3Ω
i3
gu
2−5
解
设网孔电流为 i1 , i2 , i3 ,则 i3 = − gu A = −0.1u A ,所以只要列出两个网孔方程
27i1 − 18i2 = 42 −18i1 + 21i2 − 3(−0.1u A ) = 20
因 u A = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
第5章 三相电路分析

第5章三相电路一、填空题:1. 对称三相负载作Y接,接在380V的三相四线制电源上。
此时负载端的相电压等于倍的线电压;相电流等于倍的线电流;中线电流等于。
2. 有一对称三相负载接成星形联接,每相阻抗模均为22Ω,功率因数为0.8,又测出负载中的电流为10A,那么三相电路的有功功率为;无功功率为;视在功率为。
假如负载为感性设备,则等效电阻是;等效电感量为。
3. 三相对称电压是指频率、幅值、相位互差的三相交流电压,三相对称电压的瞬时值之和等于。
4. 在三相对称负载三角形连接的电路中,线电压为220V,每相电阻均为110Ω,则相电流I P=___ ____,线电流I L=___ __。
线电流比相应的相电流。
5.对称三相电路Y形连接,若相电压为()οV,则线电压ω60=tu220-sinA=u V。
AB6.三相四线制供电方式,中线的作用是使星形连接的不对称负载的对称,中线上不许接、。
7.三相电路星形连接,各相电阻性负载不对称,测得I A =2A,I B =4A,I C=4A,则中线上的电流为。
8.在三相正序电源中,若B相电压u B初相角为-90º,则线电压u AB的初相角为;若线电压u AB初相角为45º,则相电压u A的初相角为。
9.当三相对称负载的额定电压等于三相电源的线电压时,则应将负载接成;当三相对称负载的额定电压等于三相电源的相电压时,则应将负载接成。
10.三相电源的线电压对应相电压30°,且线电压等于相电压的倍;三相对称负载作三角形连接时,线电流对应相电流30°,且线电流等于相电流的倍。
11.三相交流电路中,只要负载对称,无论作何联接,其有功功率为。
12. 三相电源线电压U l =380V ,对称负载阻抗为Z =40+j30Ω,若接成Y 形,则线电流I l =______A ,负载吸收功率P =______W ;若接成Δ形,则线电流I l =______A ,负载吸收功率P =______W 。
第五章-二阶动态电路分析

(t 0)
dt
23
5-2 RLC串联电路全响应
电路如图 ,分析过程如前, 可得电路微分方程为
LC
d 2uC dt 2
RC
duC dt
uC
US
US
t0
+ uR - + uL -
R
L
+ C uC
-
上式是二阶常系数线性非齐次微分方程。它的完全解 由对应齐次方程的通解和非齐次方程特解组成。即
uC (t) uCh (t) uCp (t)
(1)当R >2 负实根;
L(即 C
R 2L
2)时L1C,S1、S2为两个不等的
(2)当R <2 L(即
C
负的共轭复根;
R )2 时1,S1、S2为一对实部为 2L LC
(3)当R =2 L(即
C
负实根;
R )2 时1,S1、S2为一对相等的 2L LC
一、过阻尼情况 (R 2 L ) C
duc dt
t0
C( K1
d K2)
0
K1 U0
K2
U0 d
uC
(t
)
et
(U
o
cos
d
t
U0 d
sin
d
t)
uC
(t)
0 d
U 0e t
cos( d t
)
arctg d
、d、o、的关系可表示为
电路中其它响应:
i(t) C
duC dt
02CU0 d
et sin dt
uL (t)
L
di dt
R1C2
R2C
2
)
du2 dt
u2
电路分析基础第四版课后习题第四章第五章第六章答案
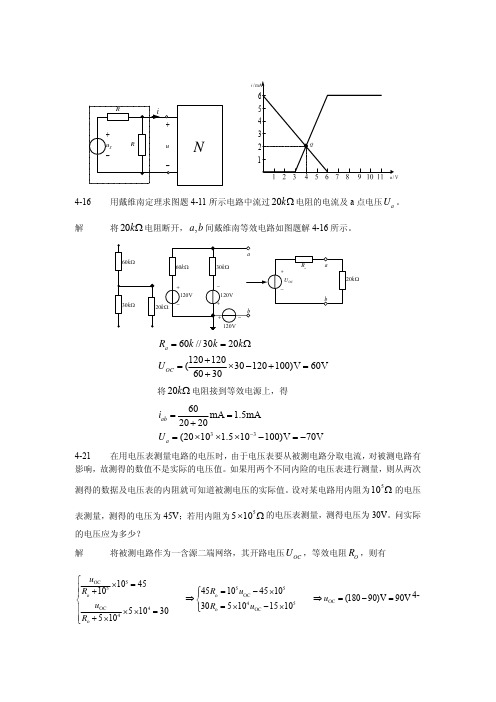
/i4-16 用戴维南定理求图题4-11所示电路中流过20k Ω电阻的电流及a 点电压。
a U 解将电阻断开,间戴维南等效电路如图题解4-16所示。
20k Ω,a bk Ω60//3020120120(30120100)V 60V6030a OCR k k k U ==Ω+=×−+=+ 将电阻接到等效电源上,得20k Ω3360mA 1.5mA2020(2010 1.510100)V 70V ab a i U −==+=×××−=− 4-21 在用电压表测量电路的电压时,由于电压表要从被测电路分取电流,对被测电路有影响,故测得的数值不是实际的电压值。
如果用两个不同内险的电压表进行测量,则从两次测得的数据及电压表的内阻就可知道被测电压的实际值。
设对某电路用内阻为的电压表测量,测得的电压为45V ;若用内阻为510Ω5510×Ω的电压表测量,测得电压为30V 。
问实际的电压应为多少? 解将被测电路作为一含源二端网络,其开路电压,等效电阻OC U O R ,则有5OC 555o o OC OC 454OCo OC 4o 10451045104510(18090)V 90V 30510151051030510u R R u u u R u R ⎧×=⎪⎧+=−×⎪⎪⇒⇒=⎨⎨=×−×⎪⎪⎩××=⎪+×⎩−=4-28 求图题4-20所示电路的诺顿等效电路。
已知:12315,5,10,R R R =Ω=Ω=Ω。
10V,1A S S u i ==解对图题4-20所示电路,画出求短路电流和等效内阻的电路,如下图所示SC i对左图,因ab 间短路,故0,0i i α==,10A 0.5A 155SC i ==+ 对右图,由外加电源法,106ab R α=Ω− 4-30 电路如图题4-22所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电容初始电压为:
零输入响应方程为:
解的形式为: 代入初始条件可得:
得:
零状态响应方程为:
其齐次为:
其特解为: 代入方程有: 可知:
通解为:
代入初始条件:
得:
根据分流关系,可知电流 的零输入响应为:
再根据回路列KVL方程:
整理可得:
5.10 如题5.10图所示电路, 时开关S位于1,电路已处于稳态。当 时开关S闭合2,求 时电流 和电压 的零输入响应和零状态响应。
得:
根据分流关系,可得:
5.7 如题5.7图所示电路,电感初始储能为零,当 时开关S闭合,试求 时电流 ,并画出其波形。
解:已知
当开关闭合时,有:
根据KVL有:
整理可得:
方程的齐次解为:
方程的特解为:
代入方程有: 可得:
全解为:
代入初始条件,可得:
得:
5.8 如题5.8图所示电路,电容初始储能为零,当 时开关S闭合,试求 时的 、 和 。
解: 时,
有:
5.4 如题5.4图所示电路,电压表的内阻 ,量程为100V。开关S在 时打开,问开关打开时,电压表是否会损坏?
解:当开关闭合时,有:
当开关打开时,有:
所产生的电压为:
可见超出了电压表的量程,因此电压表会损坏。
5.5 如题5.5图所示电路, 时已处于稳态。当 时开关S打开,求初始值 和 、 。
解:⑴ 可知电路的时间常数为:
当 时,有:
当 时,有:
由上面两式联解可得:
代入时间常数式子,得:
⑵ 此时全响应可分为零输入响应和零状态响应,而零状态响应可看成电压源和电流源分别单独作用的叠加,有:
零输入响应: 当 时,有
根据三要素公式,可得
电压源产生的零状态响应:
根据三要素公式,可得
电流源产生的零状态响应:
解: 时,有:
S打开, 时有:
电路的时间常数为:
根据三要素公式,可知:
5.14 如题5.14图所示电路, 已处于稳态,当 时开关S闭合,求 时的电流 。
解:在 ,开关闭合,根据电路的
特殊性,电流 可以看成电压源和电容
初始储能作用的叠加。可利用三要素公式
进行求解:
在 有:
由电容初始电压作用产生的电流为 ,显然有:
⑴ 求在同样初始状态下, 时的 。
⑵ 求在同样初始状态下,当 , 时的 。
5.29 如题5.29图所示电路,以 为响应。
⑴ 列出其微分方程。
⑵ 若已知L=2H,C=1F,为使其零输入响应为衰减振荡,求电阻R的取值范围。
方程解为:
代入初始条件:
零输入相应为:
零状态响应(等效电路如右),其方程为:
齐次解为:
特解为:
代入方程可得:
则零状态相应为:
代入初始条件可得:
有:
全响应为:
5.12 如题5.12图所示电路, 已处于稳态,当 时开关S闭合,闭合后经过10s后,开关又打开,求 时 。
解:
5.13 如题5.13图所示电路, 已处于稳态,当 时开关S打开,求 时 和 。
⑴ 求其阶跃响应 。
⑵ 若输入信号 的波形如图(b)所示,求 的零状态响应。
5.25 如题5.25图所示电路,求零状态响应 和 。
5.26 如题5.26(a)图所示电路,其中, 如题5.26(b)图所示, 时电路已达稳态。 时开关S断开,求 时电流 的零输入响应和零状态响应。
5.27 如题5.27图所示电路,L=8H,C=0.5F。若以 为输出,求阶跃响应;若要使 也是阶跃函数,求 和 的值。
解:根据理想变压器的特性,可将
电路等效为如图所示,有折射电阻:
对初级电流 应用三要素求解
有:
根据理想变压器的变流关系,可得:
5.21 如题5.21图所示电路, 已处于稳态。当 时开关S闭合,求 时的开路电压 。
解:由于耦合电感的次级开路,
开关闭合时,电路可等效为如图示,
以初级电流应用三要素求解,有:
则有:
根据耦合电感电压电流关系,可得:
5.22 如题5.22图所示电路,已知 , , 时开关S闭合。
⑴ 求使暂态响应分量为零的电容电压初始值。
⑵ 若 ,为使 时的 等于零,求所需的电容C的值。
5.23 已知电流波形如题5.23图所示,试用阶跃函数表示该电流。
5.24 如题5.24(a)图所示电路,以 为输出。
第五章 习题
5.1 如题5.1图所示电路, 时已处于稳态。当 时开关S打开,求初始值 和 。
如题5.2图所示电路, 时已处于稳态。当 时开关S闭合,求初始值 、 和 。
解: 时处于稳态,有:
根据电容电压、电感电流不能突变,当开关S闭合有:
5.3 如题5.3图所示电路, 时已处于稳态。当 时开关S闭合,求 和 。
解:开关闭合时,有:
而
可得:
5.19 如题5.19图所示电路, 已处于稳态。当 时,受控源的控制系数r突然由10Ω变为5Ω,求 时的电压 。
解:在稳定状态,有:
显然有:
再求电容两端的等效电阻,在有受控源时,
采用外加电压法,有:
可知等效电阻为:
有:
根据三要素公式,可得:
5.20 如题5.20图所示电路, 已处于稳态。当 时开关S闭合,求 时的电流 。
解:开关闭合时,
电阻上的电压为:
所以有
根据电容电压不能突变,开关打开时可得:
5.6 如题5.6图所示电路, 时已处于稳态。当 时开关S从1打到2,试求 时电流 ,并画出其波形。
解:开关S位于1时,有:
开关S位于2时,建立 的方程:
为等效电阻 的电压
而
可得微分方程:
初始条件:
解方程: 特征根为
则有: 代入初始条件可得:
解:根据电路结构,可看成是一个RC和
一个RL的串联,它们互不影响,有:
对于RC电路,应用三要素公式:
有:
对于RL电路,应用三要素公式:
有:
可得:
要使 也是阶跃函数,显然应有:
即: 和
联解可得:
5.28 如题5.28图所示电路, 内只含线性时不变电阻,电容的初始状态一定,已知当 , ,全响应为 , 。
根据三要素公式,可得
全响应为:
5.17 如题5.17图所示电路,N中不含储能元件,当 时开关闭合后,输出电压的零状态响应 , ;如果将2F的电容换为2H的电感,求输出电压的零状态响应 。
5.18 如题5.18图所示电路,其中,N为线性含独立源的电阻电路。当 时开关S闭合。已知 ,电流 , 。求 时的电压 。
解: 时有:
时建立方程,有:
整理可得微分方程为:
零输入响应: 代入初始条件
可得:
零状态响应:
齐次解:
特解: 代入方程可得:
则:
由初始条件 ,可知
得:
5.11 如题5.11图所示电路, 已处于稳态,当 时开关S打开,求 时电流 的零输入响应、零状态响应和全响应。
解: 时根据叠加原理有:
零输入响应,其方程为:
解:已知
开关闭合时,将电路等效为简单的RC串联,
以 建立方程,有:
代入参数有:
方程齐次解为:
方程的特解为: 代入方程可知
所以有: 代入初始条件可得:
得:
5.9 如题5.9图所示电路, 时已处于稳态。当 时开关S闭合,求 时电压 和电流 的零输入响应和零状态响应。
解:设C=0.1F,开关闭合时建立方程,有:
由12伏电压源作用产生的电流为 ,有:
可知:
得:
5.15 如题5.15图所示电路, 已处于稳态,当 时开关S从1打到2,试求 时的电流 。
5.16 如题5.16图所示电路,电容的初始电压 一定,激励源均在 时接入电路,已知当 、 时,全响应 , ;当 、 时,全响应 , 。
⑴ 求 、 和 的值。
⑵ 求当 、 时的全响应 。
