(研04)第四章 习题讲解-4
第四章重复博弈习题讲解

• (3)将(下,左)的得益改为(1,5)情况会发生质的 变化。因为此时第一阶段两博弈方都有偏离(下,右)的 动机,而上述博弈又不存在同一个阶段中同时对两博弈方 惩罚或奖励的纳什均衡,因此重复两次时不可能存在子博 弈完美纳什均衡部分实现(4,4)得益。 • 至少在部分阶段实现得益(4,4)的条件是重复博弈的 次数达到三次或以上,或者得益进一步改变到(下,右) 是原博弈的纳什均衡。如设计触发策略: • 博弈方1:第一阶段选“下“,出现结果(下,右),则 第二阶段继续选”上“,第三阶段选”中“。 • 如果第一阶段没有出现,(下,右),则第二、第三阶段 选混合策略均衡。 • 博弈方2:第一阶段选“右“,出现结果(下,右)则第 二阶段选”左“,第三阶段选”中“,否则第二、三阶段 选择混合策略的均衡。 • 均衡路径为(下,右)(上,左)(中,中)
• 答:(1)上述静态博弈有两个纯策略纳什均衡(上,左)和 (中,中)。由于策略组合(下,右)实现的得益(4,4)对 博弈方2来说已是最理想的,因此博弈方2不会有偏离的动机, 只有博弈方1可能有偏离动机,因此可设计如下触发策略。
• 博弈方1:第一阶段采取下;如果第一阶段的结果是(下,右) 则采取上,否则采取中。 • 博弈方2:第一阶段采取右;如果第一阶段的结果是(下,右) 第二阶段采取左,否则采取中。
工程力学 习题详解 第四章

n
mO ( R ) Rd M O (主矩)
———合力矩定理
M O ( R ) mO ( Fi )
n i 1
由于简化中心是任意选取的,故此式有普遍意义。 即:平面任意力系的合力对作用面内任一点之矩等于力系 中各力对于同一点之矩的代数和。
12
静力学
例题4-1
第4章 平面任意力系
F
A C B
Fx 0,
FAx FC cos 45 0 FAy FC sin 45 F 0 FC cos 45 l F 2l 0
Fy 0,
M A F 0,
解平衡方程可得
FC 2 F
D
cos 45 FAx FC cos 45 2 F 20 kN
组合梁AC和CE用铰链C相连,A端为固定端,E端 为活动铰链支座。受力如图所示。已知: l =8 m, F=5 kN,均布载荷集度q=2.5 kN/m,力偶矩的大小 M= 5 kN•m,试求固端A,铰链C和支座E的约束力。 F q B l/4
M E
A
H
C
l/4
D l/4
l/8 l/8
30
解: 1.取CE段为研究对象。受力分析如图。
例题4-5
如图所示为一悬臂梁,A为固定端,设梁上受强度
为q的均布载荷作用,在自由端B受一集中力F和一力偶
M作用,梁的跨度为l,求固定端的约束力。
q
A l
M
F
45
B
24
解:
取梁为研究对象,受力分析如图 由平衡方程
M F
45
q
A
Fx 0,
Fy 0,
FAx F cos 45 0
线性代数 课后习题详解 第四章

第四章 矩阵的初等变换与线性方程组1.把下列矩阵化为行最简形矩阵:(1) ⎪⎪⎪⎭⎫ ⎝⎛--340313021201; (2) ⎪⎪⎪⎭⎫ ⎝⎛----174034301320;(3) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311; (4) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛--3403130212011312)3()2(~r r r r -+-+⎪⎪⎪⎭⎫ ⎝⎛---020********* )2()1(32~-÷-÷r r ⎪⎪⎪⎭⎫ ⎝⎛--01003100120123~r r -⎪⎪⎪⎭⎫⎝⎛--300031001201 33~÷r ⎪⎪⎪⎭⎫ ⎝⎛--100031001201323~r r +⎪⎪⎪⎭⎫⎝⎛-1000010012013121)2(~r r r r +-+⎪⎪⎪⎭⎫⎝⎛100001000001(2) ⎪⎪⎪⎭⎫ ⎝⎛----174034301320 1312)2()3(2~r r r r -+-+⨯⎪⎪⎪⎭⎫⎝⎛---310031001320 21233~r r r r ++⎪⎪⎪⎭⎫ ⎝⎛000031001002021~÷r ⎪⎪⎪⎭⎫ ⎝⎛000031005010(3) ⎪⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311 141312323~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311 )5()3()4(432~-÷-÷-÷r r r ⎪⎪⎪⎪⎪⎭⎫⎝⎛-----221002210022100343112423213~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫⎝⎛---00000000002210032011(4) ⎪⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132 242321232~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫⎝⎛-----1187701298804202111110 141312782~r r r r r r --+⎪⎪⎪⎪⎪⎭⎫⎝⎛--4100041000202011111034221)1(~r r r r r --⨯↔⎪⎪⎪⎪⎪⎭⎫⎝⎛----0000041000111102021 32~r r +⎪⎪⎪⎪⎪⎭⎫⎝⎛--000004100030110202012.在秩是r 的矩阵中,有没有等于0的1-r 阶子式?有没有等于0的r 阶 子式?解 在秩是r 的矩阵中,可能存在等于0的1-r 阶子式,也可能存在等 于0的r 阶子式.例如,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=00000000010000100001α3)(=αR 同时存在等于0的3阶子式和2阶子式.3.从矩阵A 中划去一行得到矩阵B ,问B A ,的秩的关系怎样? 解 )(A R ≥)(B R设r B R =)(,且B 的某个r 阶子式0≠D r .矩阵B 是由矩阵A 划去一行得到的,所以在A 中能找到与D r 相同的r 阶子式D r ,由于0≠=D D r r , 故而)()(B R A R ≥.4.求作一个秩是4的方阵,它的两个行向量是)0,0,1,0,1(,)0,0,0,1,1(- 解 设54321,,,,ααααα为五维向量,且)0,0,1,0,1(1=α,)0,0,0,1,1(2-=α,则所求方阵可为,54321⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=αααααA 秩为4,不妨设⎪⎩⎪⎨⎧===)0,0,0,0,0(),0,0,0,0()0,,0,0,0(55443αααx x 取154==x x 故满足条件的一个方阵为⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-00000100000100000011001015.求下列矩阵的秩,并求一个最高阶非零子式:(1) ⎪⎪⎪⎭⎫ ⎝⎛---443112112013; (2) ⎪⎪⎪⎭⎫⎝⎛-------815073131213123; (3) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---02301085235703273812.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛---443112112013r r 21~↔⎪⎪⎪⎭⎫ ⎝⎛---443120131211 ⎪⎪⎪⎭⎫⎝⎛------564056401211~12133r r r r 2000056401211~23秩为⎪⎪⎪⎭⎫ ⎝⎛----r r 二阶子式41113-=-.(2) ⎪⎪⎪⎭⎫⎝⎛-------815073131223123⎪⎪⎪⎭⎫ ⎝⎛---------152********117014431~27122113r r r r r r 200000591170144313~23秩为⎪⎪⎪⎭⎫ ⎝⎛-----r r .二阶子式71223-=-.(3) ⎪⎪⎪⎪⎪⎭⎫⎝⎛---02301085235703273812434241322~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------023010********071210 131223~r r r r ++⎪⎪⎪⎪⎪⎭⎫⎝⎛-0230114000016000071210344314211614~r r r r r r r r -÷÷↔↔⎪⎪⎪⎪⎪⎭⎫⎝⎛-0000010*******002301秩为3 三阶子式07023855023085570≠=-=-.6.求解下列齐次线性方程组:(1) ⎪⎩⎪⎨⎧=+++=-++=-++;0222,02,02432143214321x x x x x x x x x x x x (2)⎪⎩⎪⎨⎧=-++=--+=-++;05105,0363,02432143214321x x x x x x x x x x x x (3) ⎪⎪⎩⎪⎪⎨⎧=-+-=+-+=-++=+-+;0742,0634,0723,05324321432143214321x x x x x x x x x x x x x x x x (4)⎪⎪⎩⎪⎪⎨⎧=++-=+-+=-+-=+-+.0327,01613114,02332,075434321432143214321x x x x x x x x x x x x x x x x解 (1) 对系数矩阵实施行变换:⎪⎪⎪⎭⎫ ⎝⎛--212211121211⎪⎪⎪⎪⎭⎫⎝⎛---3410013100101~即得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-==4443424134334x x x x x x x x 故方程组的解为⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1343344321k x x x x(2) 对系数矩阵实施行变换:⎪⎪⎪⎭⎫ ⎝⎛----5110531631121⎪⎪⎪⎭⎫ ⎝⎛-000001001021~ 即得⎪⎪⎩⎪⎪⎨⎧===+-=4432242102x x x x x x x x 故方程组的解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛10010*********k k x x x x(3) 对系数矩阵实施行变换:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----7421631472135132⎪⎪⎪⎪⎪⎭⎫⎝⎛1000010000100001~即得⎪⎪⎩⎪⎪⎨⎧====00004321x xx x故方程组的解为⎪⎪⎩⎪⎪⎨⎧====00004321x x x x(4) 对系数矩阵实施行变换:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----3127161311423327543⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--000000001720171910171317301~ 即得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=-=4433432431172017191713173x x x x x x x x x x故方程组的解为⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛1017201713011719173214321k k x x x x7.求解下列非齐次线性方程组:(1) ⎪⎩⎪⎨⎧=+=+-=-+;8311,10213,22421321321x x x x x x x x (2) ⎪⎪⎩⎪⎪⎨⎧-=+-=-+-=+-=++;694,13283,542,432z y x z y x z y x z y x(3) ⎪⎩⎪⎨⎧=--+=+-+=+-+;12,2224,12w z y x w z y x w z y x (4) ⎪⎩⎪⎨⎧-=+-+=-+-=+-+;2534,4323,12w z y x w z y x w z y x解 (1) 对系数的增广矩阵施行行变换,有⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛--60003411100833180311102132124~2)(=A R 而3)(=B R ,故方程组无解.(2) 对系数的增广矩阵施行行变换:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----69141328354214132⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--0000000021101201~ 即得⎪⎩⎪⎨⎧=+=--=zz z y z x 212亦即⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛021112k z y x(3) 对系数的增广矩阵施行行变换:⎪⎪⎪⎭⎫ ⎝⎛----111122122411112⎪⎪⎪⎭⎫ ⎝⎛-000000100011112~ 即得⎪⎪⎪⎩⎪⎪⎪⎨⎧===++-=0212121w z z y y z y x 即⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛00021010210012121k k w z y x(4) 对系数的增广矩阵施行行变换:⎪⎪⎪⎭⎫⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛-----000007579751025341253414312311112~⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----000007579751076717101~ 即得⎪⎪⎪⎩⎪⎪⎪⎨⎧==--=++=w w z z w z y w z x 757975767171 即⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛00757610797101757121k k w z y x8.λ取何值时,非齐次线性方程组 ⎪⎩⎪⎨⎧=++=++=++2321321321,,1λλλλλx x x x x x x x x (1)有唯一解;(2)无解;(3)有无穷多个解?解 (1) 0111111≠λλλ,即2,1-≠λ时方程组有唯一解.(2) )()(B R A R < ⎪⎪⎪⎭⎫ ⎝⎛=21111111λλλλλB ⎪⎪⎭⎫ ⎝⎛+-+----22)1)(1()2)(1(00)1(11011~λλλλλλλλλλ由0)1)(1(,0)2)(1(2≠+-=+-λλλλ 得2-=λ时,方程组无解.(3) 3)()(<=B R A R ,由0)1)(1()2)(1(2=+-=+-λλλλ, 得1=λ时,方程组有无穷多个解.9.非齐次线性方程组⎪⎩⎪⎨⎧=-+=+--=++-23213213212,2,22λλx x x x x x x x x 当λ取何值时有解?并求出它的解.解 ⎪⎪⎪⎪⎭⎫ ⎝⎛+-----⎪⎪⎪⎭⎫ ⎝⎛----=)2)(1(000)1(321101212111212112~2λλλλλλB方程组有解,须0)2)(1(=+-λλ得2,1-==λλ当1=λ时,方程组解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛001111321k x x x当2-=λ时,方程组解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛022111321k x x x10.设⎪⎩⎪⎨⎧--=-+--=--+=-+-,1)5(42,24)5(2,122)2(321321321λλλλx x x x x x x x x问λ为何值时,此方程组有唯一解、无解或有无穷多解?并在有无穷多解时求解.解 ⎪⎪⎪⎭⎫ ⎝⎛---------154224521222λλλλ初等行变换~⎪⎪⎪⎪⎪⎭⎫⎝⎛---------2)4)(1(2)10)(1(00111012251λλλλλλλλ 当0≠A ,即02)10()1(2≠--λλ 1≠∴λ且10≠λ时,有唯一解.当02)10)(1(=--λλ且02)4)(1(≠--λλ,即10=λ时,无解.当02)10)(1(=--λλ且02)4)(1(=--λλ,即1=λ时,有无穷多解.此时,增广矩阵为⎪⎪⎪⎭⎫ ⎝⎛-000000001221原方程组的解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛00110201221321k k x x x (R k k ∈21,)11.试利用矩阵的初等变换,求下列方阵的逆矩阵:(1) ⎪⎪⎪⎭⎫⎝⎛323513123; (2) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023. 解 (1)⎪⎪⎪⎭⎫ ⎝⎛100010001323513123⎪⎪⎪⎭⎫ ⎝⎛---101011001200410123~⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----10121121023200010023~⎪⎪⎪⎪⎪⎭⎫⎝⎛----2102121129227100010003~⎪⎪⎪⎪⎪⎭⎫⎝⎛----21021211233267100010001~故逆矩阵为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----21021211233267(2) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----10000100001000011210232112201023 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----00100301100001001220594012102321~ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------20104301100001001200110012102321~ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-------106124301100001001000110012102321~ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----------10612631110`1022111000010000100021~ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-------106126311101042111000010000100001~ 故逆矩阵为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-------1061263111010421112.(1) 设⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--=132231,113122214B A ,求X 使B AX =;(2) 设⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛---=132321,433312120B A ,求X 使B XA =. 解 (1) ()⎪⎪⎪⎭⎫ ⎝⎛----=132231113122214B A 初等行变换~⎪⎪⎪⎭⎫ ⎝⎛--412315210100010001 ⎪⎪⎪⎭⎫ ⎝⎛--==∴-4123152101B A X (2) ⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛132321433312120B A 初等列变换~⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---474112100010001 ⎪⎪⎭⎫ ⎝⎛---==∴-4741121BA X .。
《理论力学》第四章 静力学应用专题习题解
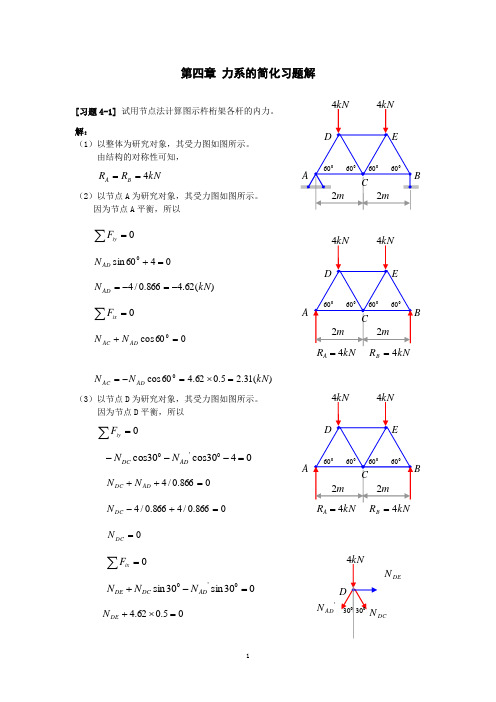
第四章 力系的简化习题解[习题4-1] 试用节点法计算图示杵桁架各杆的内力。
解:(1)以整体为研究对象,其受力图如图所示。
由结构的对称性可知, kN R R B A 4==(2)以节点A 为研究对象,其受力图如图所示。
因为节点A 平衡,所以0=∑iyF0460sin 0=+AD N)(62.4866.0/4kN N AD -=-=0=∑ixF060cos 0=+AD AC N N)(31.25.062.460cos 0kN N N AD AC =⨯=-= (3)以节点D 为研究对象,其受力图如图所示。
因为节点D 平衡,所以 0=∑iyF0430cos 30cos 0'0=---AD D C N N 0866.0/4=++AD D C N N 0866.0/4866.0/4=+-D C N0=DC N0=∑ixF030sin 30sin 0'0=-+AD D C D E N N N 05.062.4=⨯+DE NkN4)(akN4AB RkN 2AC23N A )(31.2kN N DE -=(4)根据对称性可写出其它杆件的内力如图所示。
[习题4-2] 用截面法求图示桁架指定杆件 的内力。
解:(a)(1)求支座反力以整体为研究对象,其受力图如图所示。
由对称性可知,kN R R B A 12==(2)截取左半部分为研究对象,其受力图 如图所示。
因为左半部分平衡,所以0)(=∑i CF M0612422843=⨯-⨯+⨯+⨯N 063243=⨯-++N )(123kN N =kN2AC23N A0=∑ixF0cos cos 321=++N N N αθ01252252421=+⋅+⋅N N012515221=+⋅+⋅N N0512221=++N N ……..(1) 0=∑iyF02812sin sin 21=--++αθN N025*******=+⋅+⋅N N02525121=+⋅+⋅N N052221=++N N0544221=++N N ……..(2) 05832=-N)(963.53/582kN N ==)(399.1652963.5252221kN N N -=-⨯-=--=解:(b )截取上半部分为研究对象,其受力图如图所示。
教育学第四章习题含答案

第四章教师与学生练习题一、选择题1、我国首次以法律形式明确规定“国家实行教师资格制度”的文件是(D )A、《教师资格条例》B、《教师资格认定的过渡办法》C、《教师资格条例》实施办法D、《中华人民共和国教师法》2、“以身立教”、“为人师表”体现了教师劳动的( A )特点。
A、示范性B、复杂性C、创造性D、劳动方式个体性3、教师的工作目的和使命是(C )A、热爱教育事业B、热爱学生C、教书育人D、创新开拓4、陶行知先生的“捧着一颗心来,不带半根草去”的教育信条体现了教师的( B )素养。
A、教育理论知识B、崇高的职业道德C、文化学科知识D、具备相应的专业知识5、教师的地位一般是指教师的( A )A、社会地位B、经济地位C、文化地位D、政治地位6、“道之所存,师之所存也”体现了教师职业的( C )A、示范者角色B、授业解惑者角色C、传道者角色D、研究者角色7、具有先进的教学理念属于教师的( C )A、职业首先素养B、能力素养C、教育专业素养D、心理素养8、在课程改革过程中,教师成为学生学习的合作者,由教学中的主角转向( B )A、知识的传授者B、平等中的首席C、教学的组织者D、行为的示范者9、现代师生关系的核心是( C )A、以诚相待B、互助互惠C、民主平等D、和谐亲密10、下面哪种表现说明罗森塔尔效应( B )A、老师让背书,学生们认真地背书B、老师对学生说:“你很聪明,只要认真学习,成绩一定会提高。
”结果这个学生成绩提高了C、学生犯了错误,老师批评了他D、老师穿的很漂亮,结果学生们在课堂上积极地配合老师11、学生具有发展的可能性和( D )A、潜在性B、现实性C、特殊性D、可塑性12、“师者,所以传道、授业、解惑也”出自( B )A、《学记》B、《师说》C、《论语》D、《春秋》13、人们常说:“教学有法、而无定法”,这句话反映了教师应具备的素养是( C )A、良好的语言表达能力B、较强的组织能力C、创造能力D、观察能力二、判断题1、从狭义来看,教师指学校的专职工作人员,是一种专门的职业。
高等代数第四章及其习题答案
α b11
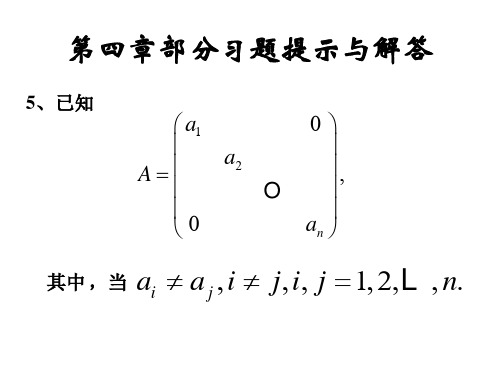
A1 0
= B1 0
β a11b11 a11β + α B1
A1 B1
,
为上三角形矩阵, 由归纳法假设知 A1 B1 为上三角形矩阵,故 AB 为上三 角形矩阵。 角形矩阵。
2)设 A = ( aij ) 为一可逆的上三角形矩阵,则 ) 为一可逆的上三角形矩阵, nn
= ε iT A j L 0 L L L 0 L a jn i 行 . L 0 L L L 0
0 M 0 a1i AEij = ( B1 , L , Bn ) ε j = Bi ε j = M ( 0, L , 0,1, 0, L , 0 ) a 0 ni M 0 0 0 = L 0 L L L 0 0 0 a1i a2 i L ani 0 L L 0 . L L L 0 L 0 0 L
T
y1 n T T 2 ( Ax) Ax = y y = ( y1 ,L, yn ) M = ∑ yi = 0, y i =1 n
从而 yi = 0, i = 1, L, n , 即 y = Ax = 0 ,由
x 的任意性知 Aε j = 0, j = 1,L , n ,其中
为数量矩阵. 为数量矩阵 级矩阵可交换, 注:因 A 与所有 n 级矩阵可交换,故 A 一定与 可交换, E i j ( i , j = 1, L , n ) 可交换,于是 AEij = Eij A.
10、已知 A为实对称矩阵 且 A2 = 0 , 不妨设 A = aij 、 为实对称矩阵, 阶矩阵, 为 n 阶矩阵, = x
T
( )
nn
线性代数 (清华大学出版)课后习题部分解答(第四章)

第四章课后习题 及解答1. 证明:T )(1,1,1,11=α, T )(1,1,1,12--=α, T )(1,1,1,13--=α, T )(1,1,1,14--=α是4R 的一组基, 并求T )(1,1,2,1=β在这组基下的坐标.证明:0161111111111111111,,,4321≠-=------=)(αααα.R ,,,44321的一组基是αααα∴设β在这组基下的坐标为x ,则x )(4321,,,ααααβ=,从而 βαααα14321,,,-=)(x⎝⎛⎪⎪⎪⎪⎪⎭⎫--→→⎝⎛⎪⎪⎪⎪⎪⎭⎫------4141414510001000010000111211111111111111111⎪⎪⎪⎪⎪⎭⎫⎝⎛--=∴111541x 2. 已知3R 的两组基为.6,1,1,1,2,5,4,1,3,1,7,3,3,3,2,1,2,1T3T 2T 1T1T 2T 1)()()()()()(-======βββααα求:(1)向量T2,6,3)(=γ在基{}321,,ααα下的坐标; (2)基{}321,,ααα到基{}321,,βββ的过渡矩阵; (3)用公式(4.7)求γ在基{}321,,βββ下的坐标。
解:(1)设γ在基{}321,,ααα下的坐标为x ,则:x )(321,,αααγ=从而 γααα1321,,-=)(x⎪⎪⎪⎭⎫- ⎝⎛→→ ⎝⎛⎪⎪⎪⎭⎫112100010001263131732321 ⎪⎪⎪⎭⎫⎝⎛-=∴112x(2)设基{}321,,ααα到基{}321,,βββ的过渡矩阵为A ,则:A ,,,,321321)()(αααβββ=从而 )()(3211321,,,,A βββααα-= ⎪⎪⎪⎭⎫--- ⎝⎛→→ ⎝⎛⎪⎪⎪⎭⎫-8124920941712710010001614121153131732321 ⎪⎪⎪⎭⎫⎝⎛---=∴81249209417127A (3)设γ在基{}321,,βββ下的坐标为y ,则:x y 1A -= ⎪⎪⎪⎭⎫-⎝⎛→→ ⎝⎛⎪⎪⎪⎭⎫----4832534153100100111281249209417127⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=∴83106153414832534153y3. 已知4R 的两组基为.2,1,3,1,2,1,1,2,2,2,1,0,1,0,1,21,0,1,1,1,1,2,1,1,1,1,1,0,1,2,1T4T3T2T1T4T 3T 2T 1)()()()()()()()(=-===--=-=-=-=ββββαααα(1)求基{}4321,,,αααα到基{}4321,,,ββββ的过渡矩阵;若γ在基{}4321,,,αααα下的坐标为T 0,0,0,1)(,求γ在基{}4321,,,ββββ下的坐标.(2)求基{}4321,,,ββββ到基{}4321,,,αααα的过渡矩阵;若ξ在基{}4321,,,ββββ下的坐标为T 0,1,2,1)(-,求ξ在基{}4321,,,αααα下的坐标.(3)已知向量α在基{}4321,,,αααα下的坐标为T 0,1,2,1)(-,求它在基{}4321,,,ββββ下的坐标.解:(1)设基{}4321,,,αααα到基{}4321,,,ββββ的过渡矩阵为A ,则:A ,,,,,,43214321)()(ααααββββ=从而 )()(432114321,,,,,,A ββββαααα-=⎪⎪⎪⎪⎪⎭⎫⎝⎛→→⎝⎛⎪⎪⎪⎪⎪⎭⎫------0111101011100110001000010000122211120311112021110011112121111 ⎪⎪⎪⎪⎪⎭⎫⎝⎛=∴010111010111001A 设γ在基{}4321,,,ββββ下的坐标为y ,则:⎪⎪⎪⎪⎪⎭⎫⎝⎛=0001A 1-y⎪⎪⎪⎪⎪⎭⎫⎝⎛→→⎝⎛⎪⎪⎪⎪⎪⎭⎫101-01000100001000010001010111010111001 ⎪⎪⎪⎪⎪⎭⎫⎝⎛=∴101-0y(2) 设基{}4321,,,ββββ到基{}4321,,,αααα的过渡矩阵为B ,则:B ,,,,,,43214321)()(ββββαααα= ),,,(),,,(432114321B ααααββββ-=⎪⎪⎪⎪⎪⎭⎫----⎝⎛→→⎝⎛⎪⎪⎪⎪⎪⎭⎫------11111000001111101000100001000011110111121211112221112031111202⎪⎪⎪⎪⎪⎭⎫⎝⎛----=∴1111100000111110B设ξ在基{}4321,,,αααα下的坐标为x ,则:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=1131012101011101011100101-21A x(3)设α在基{}4321,,,ββββ下的坐标为z ,则:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎪⎪⎭⎫⎝⎛----=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=20130121111110000011111001-21B z 4. 在4R 中找一个向量γ,它在自然基{}4321,,,εεεε和基T4T3T2T13,1,6,6,1,2,3,5,0,1,3,0,1,1,1,2)()()()(===-=ββββ下有相同的坐标.解:设所求坐标为x ,则它满足:x x )()(43214321,,,,,,ββββεεεε= 即:0211111163216501=⎪⎪⎪⎪⎪⎭⎫⎝⎛-x⎪⎪⎪⎪⎪⎭⎫⎝⎛→→⎪⎪⎪⎪⎪⎭⎫⎝⎛-000110010101001211111163216501 ∴此齐次线性方程组的一般解为:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=1111k x ⎪⎪⎪⎪⎪⎭⎫⎝⎛---==∴1111,,,4321k x )(可取εεεεγ 5. 已知)()()(2,2,1,1,1,1,3,2,1,1,2,1---=-=-=γβα。
在职研究生-心理学-第四章-感觉和知觉练习题(含答案)

第四章感觉与知觉一、填空题1关系。
23、观察的品质包括:4、运动知觉是指个体对物体空间位移的反应,可分为567.89觉。
10.观察的品质有观察的目的性、二、单项选择题1、知觉条件在一定的范围内发生变化,而知觉对象的影响仍然相对不变的特性称为知觉的()。
A选择性B整体性C理解性D恒常性2、两个静态的物体按一定的时间依次出现,使人觉得是一个动态的物体,这种知觉称为()。
A真动知觉B似动知觉C幻觉D时间错觉3、月朗星稀是感觉的()现象。
A适应现象B对比C后象征D视觉障碍4、胃的剧烈收缩所引起的疼痛属于()。
A内受感觉B本受感觉C外受感觉D运动觉5、入芝兰之室久而不闻其香,属于感觉的()。
A继进对比B回想C适应D继时对比6、对事物的各种属性,各个部分以及它们之间的关系的综合的整体的直接反映称为()。
A思维B感觉C知觉D概括7、个体对同一物体的凹凸或对不同物体的远近的反应称为()知觉。
A深度B大小C形状D面积8、视觉属于()。
A内受感觉B本受感觉C机体觉D外受感觉9、个体对客观现象的延续性和顺序性的反应是()知觉。
A运动B空间C方位D时间10、机体位置运动状态的反应是()感觉。
A外受B内受C本受D皮肤11、费希纳指出符合对数定律的是()。
A 心理量和物理量的关系B心理量变化和物理量C物理量的变化和心理量D感觉和感觉阈限12、最简单最低级的心理现象是()A 感觉B知觉C记忆D注意13、内脏痛觉属于()A外受感觉B本受感觉C内受感觉D感受性14、从黑暗处到明亮处感受性降低的过程叫()A嗅觉B皮肤觉C暗适应D明适应15、没有适应现象的感觉是()A嗅觉B皮肤温度觉C触压觉D痛觉16.人脑对直接作用于感觉器官的客观事物的整体属性的反映是( ):A.感觉B.反应c.知觉D.阈限17.人对最小的客观刺激量的感觉能力是( ):A.感觉阈限B.绝对感觉阈限C绝对感受性D.差别感受性18.闻到苹果香味,看到苹果红色外观出磨苹果感到光滑等引起的心理活动是( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
TH
TL
∴该循环可以进行,但不可逆。
(2) 由热力学第一定律有: QL = QH -W0 = 2000-1800 = 200 (J)
Siso
QH QL 2000 200 0.33(J/K)<0 TH TL 2000 300
6
例5:某热机循环,工质从温度为 TH = 2000 K 的高温热源吸热 QH, 并向温度为TL = 300 K的低温热源放热 QL。在下列条件下,试根据孤立 系统熵增原理,确定该热机循环是否可以进行?是否可逆?(1) QH = 1500 J,QL = 800 J;(2) QH = 2000 J,净功W0 = 1800 J。 解:(1) 将高温热源 HR、低温热源 LR和热机 E划在一孤立系统内, ∵工质经循环恢复到原来状态,∴ΔSE = 0 则 S S S S QH QL 0 iso HR LR E
9
(2)若将此热机当制冷机用,使其逆行,显 然不可能进行,因为根据上面的分析,此热机循 环是不可逆循环。(当然也可再用上述 2 种方法 中的任一种,重新判断。) 欲使制冷循环能从冷源吸热 800 kJ,假设至 少需耗功 Wmin(可逆循环时耗功最少),根据孤 立系统熵增原理,此时ΔSiso = 0,如图所示。 ΔSiso =ΔSH +ΔSL +ΔSE = |Q1|/T1-|Q2|/T2 + 0
ΔSiso= ΔSH + ΔSL + ΔSE
式中: ΔSH 和ΔSL 分别为热源 T1 和冷源 T2 的熵变;ΔSE 为循环的熵变, 即工质的熵变。
∵工质经循环恢复到原来状态,∴
ΔSE = 0 而热源放热,∴ ΔSH =-|Q1|/T1 = -2000/973 = -2.055 (kJ/K)
8
冷源吸热,∴ ΔSL =|Q2|/T2 = 800/303 = 2.640 (kJ/K) 孤立系统的熵变为 ΔSiso= ΔSH +ΔSL +ΔSE = -2.055 + 2.640 + 0 = 0.585 (kJ/K) >0 ∴此循环能实现。
例1:下列说法是否正确? (1)机械能可完全转化为热能,而热能却不能完全转化为机械 能。 (2) 热机的热效率一定小于1。 (3)循环功越大,热效率越高。 (4)一切可逆热机的热效率都相等。 (5)系统温度升高的过程一定是吸热过程。 (6)系统经历不可逆过程后,熵一定增大。 (7)熵产大于零的过程必为不可逆过程。
3
例2:在绝热膨胀过程中,工质可对外做功,这是否违背热力 学第一定律或热力学第二定律?
答:根据热力学第一定律 Q =ΔU + W,绝热膨胀时,系统对
外所做的功来源于系统热力学能的减小,∴不违背热力学第一 定律。
绝热可逆膨胀时,熵变为 0;绝热不可逆膨胀时,熵增加。
而依据热力学第二定律应有: dS≥δQ/T = 0, ∴不违背热力学 / T 进行计算。借助可逆过程的熵变公式 S 1 Q / T ,
2
(工质)温度相等的假想热源吸热的,这样,假想热源的温度就
11
4
完全相等?
q2 w T2 1 与 t 1 是否 例3:循环热效率公式 t T1 q1 q1
答:前者适用于任何热机(可逆或不可逆),后者仅适
用于可逆热机。
5
例4:(1)根据热力学第二定律,热量中只有一部分转换为有用功; 而根据热力学第一定律,理想气体在定温过程中吸收的热量,可以全部转 换为对外的有用功。两者是否有矛盾?如何解释? 答:(1)热力学第二定律的实质是说,热变功必须有补充条件:向低 温热源放热或者伴随有压力、温度的降低。理想气体的定温过程就是以压 力降低为补充条件的,当压力降低到与环境平衡时,膨胀过程即终止,即 这种过程不会无限延续下去。要想继续下去,必须构成循环,这就要求向 低温热源放热。 ∴上述说法均不违背热力学第二定律。 (2)与大气温度相同的压缩空气,可以在大气温度下从单一热源—大 气中吸收热量并全部转变 为功,这是否违反热力学第二定律?为什么? (2)热力学第二定律的实质可以表述为工质若从单一热源吸热并向外 做功,必须伴随有相应的补偿过程。压缩空气从大气中吸热并做功的过程, 伴随着压力降低的补偿过程, ∴吸热做功的过程可以实现,但这一过程 不会永远持续下去,一旦与大气之间的压力差为 0,即补偿条件不再存在 时,向外做功也就停止了。
1
例1:下列说法是否正确? (1)机械能可完全转化为热能,而热能却不能完全转化为机械能。 答:对于单个过程而言,机械能可完全转化为热能,热能也能完全转化 为机械能,例如定温膨胀过程。
对于整个循环来说,机械能可完全转化为热能,而热能却不能完全转化 为机械能。
(2) 热机的热效率一定小于1。 答:热源相同时,卡诺循环的热效率是最高的,且小于1,∴一切热机 的热效率均小于1。 (3)循环功越大,热效率越高。 答:循环ηt = w /q1,即热效率不仅与循环功有关,还与吸热热效率是循 环功与吸热量之比,量有关。 ∴循环功越大,热效率不一定越高。 (4)一切可逆热机的热效率都相等。 答:可逆热机的热效率与其工作的热源温度有关,在热源相同的条件下, 一切可逆热机的热效率都相等。
【方法 2】:利用卡诺定理来判断循环是否可行。 若在 T1 和 T2 之间进行一卡诺循环,则卡诺循环热效率为
ηt,c = 1-T2/T1 = 1-303/973 = 68.9%
而本题欲设计循环的热效率为 ηt = W/Q1 = 1-Q2/Q1 = 1-800/2000 = 60% <ηt,c 即欲设计循环的热效率比卡诺循环的低,是不可逆循环,∴循环可行。
7
该循环违背孤立系统的熵增原理, ∴是不可能进行的。
例6:欲设计一热机,使之能从温度为 973 K 的高温热源吸热2000 kJ, 并向温度为 303 K 的冷源放热 800 kJ。(1)问此循环能否实现?(2) 若把此热机当制冷机用,从冷源吸热 800 kJ,是否可能向热源放热2000 kJ?欲使之从冷源吸热 800 kJ,至少需耗多少功? 解:(1)【方法1】:利用孤立系统熵增原理来判断循环是否可行。 如图所示,孤立系统由热源、冷源及热机组成,因此
= (|Q2| + Wmin)/T1-|Q2|/T2
= (800 + Wmin)/973-800/303 = 0 ∴解得 Wmin = 1769 (kJ)
10
讨论: 水的吸热升温过程的熵变计算,由于水温度在变,因此只能 用 温度只能是水(工质)的温度,即认为水是可逆地从温度与水 是水(工质)的温度。
2
(5)系统温度升高的过程一定是吸热过程。 答:系统温度的升高可以通过对系统做功来实现,例如气 体的绝热压缩过程,气体温度是升高的。
(6)系统经历不可逆过程后,熵一定增大。
答: dS = dSf + dSg =δQ/T + dSg。系统经历绝热不可逆过 程,熵一定增大。系统经历不可逆放热过程,熵可能减小。 系统经历不可逆循环,熵不变。只有孤立系统的熵只能增加。 (7)熵产大于零的过程必为不可逆过程。 答:熵产就是由于不可逆因素引起的熵增, ∴熵产大于零 的过程必为不可逆过程。
