立体几何复习(三)-空间角的求法
空间向量求角

空间的角常见的有:线线角、线面角、面面角
一、复习引入
用空间向量解决立体几何问题的“三步曲”。
(1)建立立体图形与空间向量的联系,用空间向 量表示问题中涉及的点、直线、平面,把立体几何 问题转化为向量问题;(化为向量问题) (2)通过向量运算,研究点、直线、平面之间的 位置关系以及它们之间距离和夹角等问题;
再次演示课件
法向量法
n1,n2
n2
n1,n2 n2
n1
n1
l
l
cos cos n1, n2 cos cos n1, n2
结论:cos cos n1, n2
注意法向量的方向:同进 同出,二面角等于法向量
夹角的补角;
关键:观察二面角的范围
一进一出,二面角等于法 向量夹角
四3 、实教践学操过作程的设计与实施
问题1:
二面角的平面角AOB 能否转化成向量的夹角?
B
O l
A
AOB OA,OB
二面角 OA,OB
四、教学过程的设计与实施
2 探究方法
二面角 n1, n2
要点梳理
②方向向量法:
将二面角转化为二面角的两个面的方向向量(在 二面角的面内且垂直于二面角的棱)的夹角.
设二面角α-l-β的大小为θ,其中
z
S
O
Cy
B
sin cos OS, n OS n 2 6
OS n 1 6 3
C(0,1,0); O(0,0,0);
S(0,0,1), 于是我们有
SA =(2,0,-1);AB =(-1,1,0);
OB =(1,1,0);OS =(0,0,1);
立体几何综合复习——空间角(完整版)

立体几何专题复习-----空间角的求法(一)异面直线所成的角:定义:已知两条异面直线,a b ,经过空间任一点O 作直线//,//a a b b '',,a b ''所成的角的大小与点O 的选择无关,把,a b ''所成的锐角(或直角)叫异面直线,a b 所成的角(或夹角).为了简便,点O 通常取在异面直线的一条上理解说明:(1)平移法:即根据定义,以“运动”的观点,用“平移转化”的方法,使之成为相交直线所成的角。
(2)异面直线所成的角的范围:]2,0(π(3)异面直线垂直:如果两条异面直线所成的角是直角,则叫两条异面直线垂直.两条异面直线,a b 垂直,记作a b ⊥. (4)求异面直线所成的角的方法:法1:通过平移,在一条直线上找一点,过该点做另一直线的平行线;法2;找出与一条直线平行且与另一条相交的直线,那么这两条相交直线所成的角即为所求(5).向量法: CDAB CD AB →→=.cos θ(二)直线和平面所成的角1.线面角的定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角2、记作:θ;3、范围:[0,2π]; 当一条直线垂直于平面时,所成的角θ=2π,即直线与平面垂直;1.二面角的平面角:(1)过二面角的棱上的一点O 分别在两个半平面内作棱的两条垂线,OA OB ,则AOB ∠叫做二面角lαβ--的平面角(2)一个平面垂直于二面角l αβ--的棱l ,且与两半平面交线分别为,,OA OB O 为垂足,则AOB ∠也是l αβ--的平面角说明:(1)二面角的平面角范围是[0,180];(2)二面角的平面角为直角时,则称为直二面角,组成直二面角的两个平面互相垂直 (3)二面角的平面角的特点:1)角的顶点在棱上 ;2)角的两边分别在两个面内 ;3)角的边都要垂直于二面角的棱。
2、作二面角的平面角的常用方法:①、点P 在棱上——作垂直于棱的直线(如图1) ;②、点P 在一个半平面——三垂线定理法;(如图2) ③、点P 在二面角内——垂面法。
立体几何-空间角求法题型(线线角、线面角、二面角)

空间角求法题型(线线角、线面角、二面角)空间角能比较集中的反映学生对空间想象能力的体现, 也是历年来高考命题者的热点, 几乎年年必考。
空间角是线线成角、线面成角、面面成角的总称。
其取值范围分别是:0° < 90°、0°< < 90°、0° < 180°。
空间角的计算思想主要是转化:即把空间角转化为平面角,把角的计算转化到三角形边角关系或是转 化为空间向量的坐标运算来解。
空间角的求法一般是:一找、二证、三求解,手段上可采用:几何法(正 余弦定理)和向量法。
下面举例说明。
一、异面直线所成的角:例1如右下图,在长方体 ABCD A i BiGD i 中,已知AB 4 , AD 3, AA 2。
E 、F 分别是线段AB 、BC 上的点,且EB FB 1。
求直线EC i 与FD i 所成的角的余弦值。
思路一:本题易于建立空间直角坐标系,uuu uuu把EC i 与FD i 所成角看作向量 EC 与FD 的夹角,用向量法求 解。
思路二:平移线段C i E 让C i 与D i 重合。
转化为平面角,放到 三角形中,用几何法求解。
(图I )uuu uju umr解法一:以A 为原点,ABAD'AA 分别为x 轴、y 轴、z 轴的•••直线EC i 与FD i 所成的角的余弦值为 --- I4解法二: 延长 BA 至点 E i ,使 AE i =I ,连结 E i F 、DE i 、D i E i 、DF , 有D i C i //E i E , D i C i =E i E ,则四边形 D i E i EC i 是平行四边形。
则 E i D i //EC i 于是/ E i D i F 为直线EC i 与FD i 所成的角。
在 Rt △ BE i F 中, E i F -J E i F 2 BF 2「5 2 i 2 「‘莎。
立体几何-空间角求法题型(线线角、线面角、二面角)

空间角求法题型(线线角、线面角、二面角)空间角能比较集中的反映学生对空间想象能力的体现,也是历年来高考命题者的热点,几乎年年必考。
空间角是线线成角、线面成角、面面成角的总称。
其取值范围分别是:0°< θ ≤90°、0°≤ θ ≤90°、0°< θ ≤180°。
空间角的计算思想主要是转化:即把空间角转化为平面角,把角的计算转化到三角形边角关系或是转化为空间向量的坐标运算来解。
空间角的求法一般是:一找、二证、三求解,手段上可采用:几何法(正余弦定理)和向量法。
下面举例说明。
一、异面直线所成的角:例1如右下图,在长方体1111ABCD A B C D -中,已知4AB =,3AD =,12AA =。
E 、F 分别是线段AB 、BC 上的点,且1EB FB ==。
求直线1EC 与1FD 所成的角的余弦值。
思路一:本题易于建立空间直角坐标系,把1EC 与1FD 所成角看作向量EC 1与FD 的夹角,用向量法求解。
思路二:平移线段C 1E 让C 1与D 1重合。
转化为平面角,放到三角形中,用几何法求解。
(图1)解法一:以A 为原点,1AB AD AA 、、分别为x 轴、y 轴、z 轴的正向建立空间直角坐标系,则有 D 1(0,3,2)、E (3,0,0)、F (4,1,0)、C 1(4,3,2),于是11(1,3,2),(4,2,2)EC FD ==-设EC 1与FD 1所成的角为β,则:112222221121cos 14132(4)22EC FD EC FD β⋅===⋅++⨯-++ ∴直线1EC 与1FD 所成的角的余弦值为2114解法二:延长BA 至点E 1,使AE 1=1,连结E 1F 、DE 1、D 1E 1、DF , 有D 1C 1//E 1E , D 1C 1=E 1E ,则四边形D 1E 1EC 1是平行四边形。
则E 1D 1//EC 1 于是∠E 1D 1F 为直线1EC 与1FD 所成的角。
《立体几何初步》复习

4.(2019·全国Ⅲ)如图,点N为正方形ABCD的中心,△ECD为正三角形, 平面ECD⊥平面ABCD,M是线段ED的中点,则 A.BM=EN,且直线BM,EN是相交直线
√B.BM≠EN,且直线BM,EN是相交直线 C.BM=EN,且直线BM,EN是异面直线 D.BM≠EN,且直线BM,EN是异面直线
5 5.
即
AO
与平面
ABCD
所成角的正切值为
5 5.
(3)平面AOB与平面AOC所成角的大小.
解 由(1)可知OC⊥平面AOB. 又∵OC⊂平面AOC,∴平面AOB⊥平面AOC. 即平面AOB与平面AOC所成的角为90°.
反思 感悟
(1)求异面直线所成的角常用平移转化法(转化为相交直线的 夹角). (2)求直线与平面所成的角常用射影转化法(即作垂线、找射影). (3)二面角的平面角的作法常有三种:①定义法;②三垂线法; ③垂面法.
(2)BE∥平面PAD;
证明 因为AB∥CD,CD=2AB,E为CD的中点, 所以AB∥DE,且AB=DE. 所以四边形ABED为平行四边形,所以BE∥AD. 又因为BE⊄平面PAD,AD⊂平面PAD, 所以BE∥平面PAD.
(3)平面BEF⊥平面PCD.
证明 因为AB⊥AD,且四边形ABED为平行四边形, 所以BE⊥CD,AD⊥CD. 由(1)知PA⊥底面ABCD,所以AP⊥CD. 又因为AP∩AD=A,AP,AD⊂平面PAD, 所以CD⊥平面PAD,所以CD⊥PD. 因为E和F分别是CD和PC的中点, 所以PD∥EF,所以CD⊥EF. 又因为CD⊥BE,EF∩BE=E,EF,BE⊂平面BEF, 所以CD⊥平面BEF.又CD⊂平面PCD, 所以平面BEF⊥平面PCD.
立体几何专题复习(三) 空间角专题
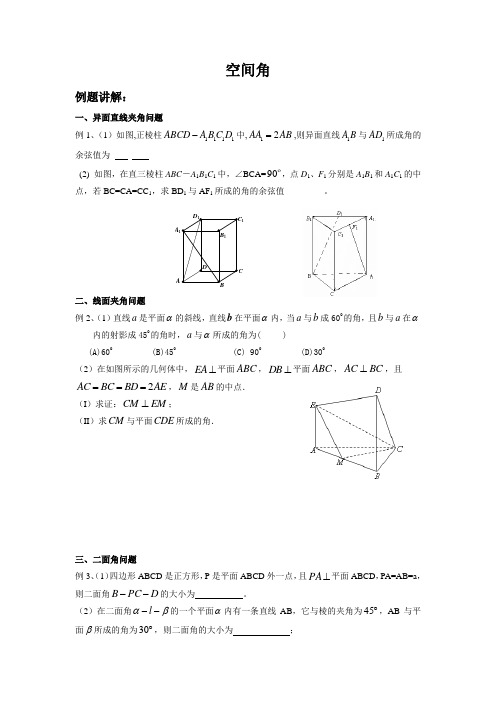
空间角例题讲解:一、异面直线夹角问题例1、(1)如图,正棱柱1111ABCD A BC D -中,12AA AB =,则异面直线1A B 与1AD 所成角的余弦值为_ _ _(2) 如图,在直三棱柱ABC -A 1B 1C 1中,∠BCA= 90,点D 1、F 1分别是A 1B 1和A 1C 1的中点,若BC=CA=CC 1,求BD 1与AF 1所成的角的余弦值_________。
二、线面夹角问题例2、(1)直线a 是平面α的斜线,直线b 在平面α内,当a 与b 成60O 的角,且b 与a 在α内的射影成45O的角时,a 与α所成的角为( ) (A)60O (B)45O (C) 90O (D)30O(2)在如图所示的几何体中,EA ⊥平面ABC ,DB ⊥平面ABC ,AC BC ⊥,且 2AC BC BD AE ===,M 是AB 的中点.(I )求证:CM EM ⊥;(II )求CM 与平面CDE 所成的角.三、二面角问题例3、(1)四边形ABCD 是正方形,P 是平面ABCD 外一点,且⊥PA 平面ABCD ,PA=AB=a ,则二面角D PC B --的大小为 。
(2)在二面角βα--l 的一个平面α内有一条直线AB ,它与棱的夹角为︒45,AB 与平面β所成的角为︒30,则二面角的大小为 ;1A(3) 如图所示,四棱锥P -ABCD 的底面ABCD 是边长为1的菱形,∠BCD =60°,E 是CD 的中点,P A ⊥底面ABCD ,P A =2.(Ⅰ)证明:平面PBE ⊥平面P AB ;(Ⅱ)求平面P AD 和平面PBE 所成二面角的平面角的正弦值大小.巩固练习:一、选择题1.已知正四棱锥S -ABCD 的侧棱长与底面边长都相等,E 是SB 的中点,则AE 、SD 所成角的余弦值为( )A.13B.23C.33D.232.如图,四棱锥S -ABCD 的底面为正方形,SD ⊥底面ABCD ,则下列结论中不.正确的是( ) A .AC ⊥SBB .AB ∥平面SCDC .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角D .AB 与SC 所成的角等于DC 与SA 所成的角3.已知三棱锥底面是边长为1的正三角形,侧棱长均为2,则侧棱与底面所成角的余弦值为( ) A.32 B.12 C.33 D.364.已知正四面体A -BCD ,设异面直线AB 与CD 所成的角为α,侧棱AB 与底面BCD 所成的角为β,侧面ABC 与底面BCD 所成的角为γ,A B C E D P则( )A.α>β>γB.α>γ>βC.β>α>γD.γ>β>α二、填空题5.已知正方体ABCD-A1B1C1D1中,E为C1D1的中点,则异面直线AE与BC所成角的余弦值为________.6.已知点O在二面角α-AB-β的棱上,点P在α内,且∠POB=45°.若对于β内异于O的任意一点Q,都有∠POQ≥45°,则二面角α-AB-β的大小是__________.7.已知点E、F分别在正方体ABCD-A1B1C1D1的棱BB1、CC1上,且B1E=2EB,CF=2FC1,则面AEF与面ABC所成的二面角的正切值等于________.三、解答题8.如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别为AB、SC的中点.(1)证明:EF∥平面SAD;(2)设SD=2CD,求二面角A-EF-D的余弦值.9.如图,正方体ABCD-A1B1C1D1中,E为棱C1D1上的动点,F为棱BC的中点.(1)求证:AE⊥DA1;(2)求直线DF与平面A1B1CD所成角的正弦值;(3)若E为C1D1的中点,在线段AA1上求一点G,使得直线AE⊥平面DFG.10.如图,在四面体ABCD中,平面ABC⊥平面ACD,AB⊥BC,AD=CD,∠CAD=30°.(1)若AD=2,AB=2BC,求四面体ABCD的体积;(2)若二面角C-AB-D为60°,求异面直线AD与BC所成角的余弦值.。
立体几何空间角 专题

PCDBA立体几何空间角 专题空间角,能比较集中反映空间想象能力的要求,历来为高考命题者垂青,几乎年年必考。
空间角是异面直线所成的角、直线与平面所成的角及二面角总称。
空间角的计算思想主要是转化:即把空间角转化为平面角,把角的计算转化到三角形边角关系或是转化为空间向量的坐标运算来解。
空间角的求法一般是:一找、二证、三计算。
异面直线所成的角的范围:090θ<≤(一)平移法【例1】已知四边形ABCD 为直角梯形,//AD BC ,90ABC ∠=,PA ⊥平面AC ,且2BC =,1PA AD AB ===,求异面直线PC 与BD 所成角的余弦值的大小。
【解】过点C 作//CE BD 交AD 的延长线于E ,连结PE ,则PC与BD 所成的角为PCE ∠或它的补角。
CE BD==PE==∴由余弦定理得222c o s 26PC CE PE PCE PC CE +-∠==-⋅∴PC 与BD 所成角的余弦值为63(二)补形法【变式练习】已知正三棱柱111ABC A B C -的底面边长为8,侧棱长为6,D为AC 中点。
求异面直线1AB 与1BC A 1C 1【答案】125直线与平面所成角的范围:090θ≤≤方法:射影转化法(关键是作垂线,找射影)【例2】如图,在三棱锥P ABC -中,90APB ∠=,60PAB ∠=,AB BC CA ==,点P 在平面ABC 内的射影O 在AB 上,的角的大小。
【解】连接OC ,由已知,OCP ∠为直线PC 与平面ABC 设AB 的中点为D ,连接,PD CD 。
AB BC CA ==,所以CD AB ⊥90,60APB PAB ∠=∠=,所以PAD ∆为等边三角形。
不妨设2PA =,则1,4OD OP AB===CD OC ∴===在RtOCP ∆中,tan 13OP OCP OC∠===【变式练习1】如图,四棱锥S ABCD -中,//AB CD ,BC CD ⊥,侧面SAB 为等边三角形。
立体几何角度的求法

3)角的边都要垂直于二面角的棱
l
B
A
此 图
×正
O
确 ?
B
10
二面角的平面角的作法:
1、定义法
A
根据定义作出来
O
l
B
2、垂面法 作与棱垂直的平面与
l
O
两半平面的交线得到
γ
A
B
3、三垂线定理法 借助三垂线定理或
其逆定理作出来
A
D
l
O
12
二面角的计算步骤:
1、找到或作出二面角的平面角 2、证明 (指出)1中的角就是所求的 角 3、计算出此角的大小
斜线和平面所成的角(或斜线和平面的夹角) • 直线和平面垂直<=>直线和平面所成的角是直角 • 直线和平面平行或在平面内<=>直线和平面所成的
角是0°
思考
• 直线与平面所成的角θ的取值范围
是: 0≤θ≤π/2
。
• 斜线与平面所成的角θ的取值范围
是: 0<θ<π/2
。
斜线和平面所成的角的求法
(1)射影法:在线上取一点作面的垂线,斜 足与垂足的连线与斜线所成的角即为所求。 问题2.正方体ABCD-A1B1C1D1中,E、F分别为BB1 、
这两个半平面叫做二面角的面。
二面角的范围
[00,1800]
3
角
二面角
图形
顶点
A 边
O
边B
从一点出发的两
定义 条射线所组成的
图形叫做角。
构成
边—点—边
(顶点)
表示法
∠AOB
A 棱a 面
B面
从一条直线出发的 两个半平面所组成 的图形叫做二面角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
A
3
思维点拨:准
确作出线线、
E
线面角是关键,
熟记正四面体 中的一些量对
B
G
D
H
解题有帮助.
F
C
作(找)---证---指出---算---结论
关键
在三角形中计算
(三)二面角:范围是[0,π].
①棱上一点定义法:常取等腰三角形底边(棱)中点.
②面上一点垂线法:自二面角的一个面上一点向另一 面引垂线,再由垂足向棱作垂线
关键在三角形中计算例1.正四面体S-ABC中,如
s
果E、F分别是SC、AB的
中点,那么异面直线EF和 E
SA所成的角=_______.
C
B
G
F
A
空间角(线线角,线面角,二面角)
作(找)---证(指出)---算---结论
在正方体AC1中,求(1)直线A1B和B1C所成的角;
(2)直线D1B和B1C所成的角 D1
D
解由:正连方结体A的C,性交质BD可于知O,,连BD结⊥OOAA1 ,BD⊥AAA1
O
C1 B1
C B
OA和AA1是平面AOA1内两条相交直线 ∴BD⊥平面AOA1 ∴BD⊥OA1 ∴∠AOA1是二面角A-BD-A1的平面角.
设正方1 ,体 作(找的 )---证棱 (指出长 )---算-为 --结论
在 AO 中 ,C O AO C1,AC 2
AO9 C0 0
(
算
)
A
二面 A角 BD C的大9小 0 0. 为
(结论)B
O
D
作(找)---证(指出)---算---结论
C
练:正方体ABCD—A1B1C1D1中,
D1
求:
A1
(1) 二面角A-BD-A1的正切值;
(2) 二面角A1-AD-B的大小.
(2)直线D1B和B1C所成的角 D1
C1
A1
E
B1
D
C
A
B
空间四边形P-ABC中,M,N分别是PB,
AC的中点,PA=BC=2,MN= 3 ,求PA与
BC所成的角?
解 :取 A中 BE ,点 连E 结 ,M E,N M,N分别 P是 B ,A的 C 中 . 点
P
EM //P,A E/N /BC
C1
A1
B1
D
C
A
B
空间角(线线角,线面角,二面角)
作(找)---证(指出)---算---结论
在正方体AC1中,求(1)直线A1B和B1C所成的角;
(2)直线D1B和B1C所成的角 D1
C1
A1
B1
O
E
D
C
F
A
B
空间角(线线角,线面角,二面角)
作(找)---证(指出)---算---结论
在正方体AC1中,求(1)直线A1B和B1C所成的角;
在 R A t1A中 O ,A1 A 1 ,A O 2 2,ta A n 1 O A A A 1 A O2
S
a a 3a
A
2a
2aD
C
2a
B
例 1 : ( 1 ) 直 三 棱 柱 ABC—
A1B1C1,∠BCA= 90 0, 点 D1 、 F1
分 别 是 A1B1 、 A1C1 的 中 点 , BC=CA=CC1,则BD1与AF1所成角
的余弦值是( A )
A. 30 B.1
C. 30 D. 15
10
2
③空间一点垂面法:自空间一点作与棱垂直的平面, 截二面角得两条射线,这两条射线所成的角.
▲当二面角的平面角不易作出时,可用面积法 直接求平面角的余弦值.
斜面面积和射影面积的关系公式: SSc os
( S为原斜面面积,S 为射影面积, 为斜面与射影所
成二面角的平面角)这个公式对于斜面为三角形,任意多 边形都成立.
(3)利用某些特殊三棱锥的有关性质,确定顶点 在底面上的射影的位置: a.如果侧棱相等或侧棱与底面所成的角相等,那 么顶点落在底面上的射影是底面三角形的外心
b.如果顶点到底面各边距离相等或侧面与底面 所成的角相等,那么顶点落在底面上的射影是 底面三角形的内心(或旁心);
c.如果侧棱两两垂直或二组对棱互相垂直(必 可推出第三组也垂直),那么顶点落在底面上 的射影是底面三角形的垂心.
15
10
( 2 ) PA 、 PB 、 PC 是 从 P 点 出
发的三条射线,每两条射线
的夹角均为 60 0 ,那么直线
PC与平面PAB所成角的余弦值 P
是( C)
A. 1 B. 2 C. 3 D. 6
2
2
3
3
C
A O
B 0
例2:在正四面体ABCD中,E、F分别为AD、BC
的中点.
3
(1)求CD与AF所成的角的余弦值; 6
▲当点的射影位置不易确定时,可用等体积法 直接求垂线长.
正三A 棱 B柱 C A1B1C1,的底面a,边 侧长 棱 长为 2a,求直 A1 线 C 与平 A1面 A B1B所成.的
C1
A1
D
B1
C
A
B
四 面 S体 AB中 C,SA ,SB ,SC 两 两,垂 S直 BA40 5, SBC60 0.求(1)BC 与 平 S面 A所 B 成;的 角 (2)SC 与 平 A面 B所 C 成 的 角;的 正 弦 值
确定射影的方法(找斜足和垂足):
(1)如果一个角所在的平面外一点到角的两边距离 相等,那么这一点在平面上的射影在这个角的平 分线上;如果一条直线与一个角的两边的夹角相 等,那么这一条直线在平面上的射影在这个角的 平分线上.
(2)两个平面相互垂直,一个平面上的点在另一个 平面上的射影一定落在这两个平面的交线上.
立体几何复习
作(找)---证---指出---算---结论
在三角形 中计算
作(找)---证---指出---算---结论
关键
在三角形中计算
(一)异面直线所成的角:范围是(0,π/2].
平移直线成相交直线:
(1)利用中位线,平行四边形;
(2)利用线段成比例;
(3)补形法.
作(找)---证---指出---算---结论
A
B
O
D
α
C
例1.如图,四面体ABCD的棱BD长为2,其余
各棱的长均是 2 , 求二面角A-BD-C的大小。
解 :取 B的 D 中 O ,连 点 A结 ,B O.(O 作)
A A A B O O A 是 B,C ,D B D C 二 C O A C B 面 B D D D 角 C 的 (平 证 ().指面 出)角
M是 EN 直 P,A B 线 所 C 成 (或 的 其 )角 补
在 ME中 N ,EM EN 1,
MN 3, si nMEN 3
MEN600 2 2
2
A
M
C N
MEN 1200
E
直线 PA,BC所成的6角00 为 B
作(找)---证---指出---算---结论
关键
在三角形中计算
(二)直线与平面所成的角:范围是[0,π/2].
