第九讲 变质量物体的运动
变质量动量定理

设第一级火箭总质量为m1 其内携带燃料的质量为m1e 且 m1e m1 第二级火箭总质量为m2 其内携带燃料的质量为 m2e m2 载荷的质量为 m p 设燃料从火箭喷出的相对速度 r =常数 方向与火箭速度方向相反 每秒喷出的燃料质量也为常数 火箭由静止开始运动 略去重力 由例6.1式(b)可得 第一级火箭的燃料全部喷射完时火箭的速度为 m1 m2 m p 1 r ln (a) m1 m2 m p m1 当第二级火箭的燃料也全部喷射完时 速度为 m2 m p 2 1 r ln m2 m p m2 (b)
§ 6-1 变质量质点的运动微分方程
1.变质量质点的运动微分方程
(e) 设作用于质点系的外力为 F
质点系在瞬时t的动量为 p1 m dm 1 质点系在瞬时t+dt的动量为 p2 (m dm)( d ) 根据动量定理
( e) (m dm)( d ) (m dm 1 ) F dt 将上式展开得 ( e) md dm dm d dm 1 F dt
i [
mi mi 1 mn m p (1 i )mi mi 1 mn m p
]
(e)
则得第n级火箭燃料燃烧完毕时的速度
n ri ln i
i 1
n
(f)
利用拉格朗日乘子法 可以求得满足下式的 i 将使火箭的总质量为最小值
(d)
如果取 m p / m 1/ 100 则 m2 / m 1 / 10, m1 / m 9 / 10 如果仍用 0.8 、 r / g 300s m/s 则由式(d)可得 2 max 7500 这显然比 m1 m2时的 2 6000m/s 要大得多 下面讨论多级火箭 ,mn 设各级火箭的质量分别为 m1 ,m2 , , 2, ,n) 各级火箭内的燃料质量为 i mi (i 1
2.7 变质量物体的运动

2.7 变质量物体的运动
(1) 吸收
由(1)(2)两式可得
mv mv mu F (t t )t
(3) (4) (5)
做泰勒展开
dF (t ) F (t t ) F (t ) t ... dt
(4)代入(3),只保留一阶无穷小,可得
mv mv mu F (t )t
向运动方向(在无外力的情况下,火箭做直 线运动)投影可得
dv dm m vr 0 dt dt
dm dv v r m
做定积分
dm v0dv vr m0 m
v m
m0 1 v vr ln v0 vr ln v0 m f (t )
7
2.7 变质量物体的运动
8
2.7 变质量物体的运动
2.7 变质量物体的运动
变质量的含义 这里的变质量是指:物体吸收外界质量, 或者释放自身质量。 另外,这里只考虑物体质量连续改变的情 况,即m(t)是对时间可微的函数。
2
2.7 变质量物体的运动
(1) 吸收
v
A, m
u
B, △m>0
v+△v
t
A, m+△m
t+△t时刻
t时刻
解:设火箭的速度为v, 燃料以绝对速度u喷出, 则火箭的运动微分方程为
d ( mv ) dm u0 dt dt
(1)
(2)
u=v+vr 其中 (2)代入(1)可得
dv dm m 变质量物体的运动 dv dm m vr 0 dt dt
例题
(3)
上式两边同时除以△t, 并取 t 0 可得
d dm ( mv ) u F (t ) dt dt
变质量的牛顿第二定律在三维坐标、平动和转动方程

变质量的牛顿第二定律在三维坐标、平动和转动方程引子:牛顿第二定律在物理学中被广泛应用,是描述物体运动状态的重要定律之一。
然而,在一些特定情况下,物体的质量可能会发生变化,这就需要引入变质量的牛顿第二定律。
本文将围绕这一主题展开讨论,分析在三维坐标、平动和转动方程中的应用。
一、牛顿第二定律的基本概念1. 牛顿第二定律的表述及原理牛顿第二定律是经典力学中的基本定律之一,它描述了物体在外力作用下的加速度与所受力的关系,通常表达为F=ma,其中F为物体所受的合外力,m为物体的质量,a为物体的加速度。
这一定律的基本原理是力是物体运动状态改变的原因,力的大小和方向决定了物体的加速度。
2. 牛顿第二定律在三维坐标中的表示在三维坐标系中,物体可能受到来自不同方向的合外力,此时可以通过矢量运算来表示牛顿第二定律。
根据矢量的性质,可以将合外力表示为一个三维矢量F=(F_x, F_y, F_z),物体的加速度也可以表示为一个三维矢量a=(a_x, a_y, a_z),则牛顿第二定律可以表示为F=ma。
二、变质量的牛顿第二定律的推导及应用1. 变质量的概念及原因在一些特定情况下,物体的质量可能会随时间变化,例如火箭发射过程中燃料消耗导致质量减小。
此时,传统的牛顿第二定律就无法准确描述物体的运动状态,需要引入变质量的概念。
2. 变质量的牛顿第二定律的推导根据牛顿第二定律的基本原理,可以推导出变质量的牛顿第二定律。
假设物体的质量随时间变化,其质量函数可以表示为m(t),则物体所受的合外力F(t)与加速度a(t)的关系可以表示为F(t)=m(t)a(t)。
在质量变化的情况下,需要考虑质量随时间的变化率dm/dt对物体运动状态的影响,进而推导出变质量的牛顿第二定律。
3. 变质量的牛顿第二定律在平动和转动方程中的应用在实际的物理问题中,变质量的牛顿第二定律被广泛应用于描述物体的平动和转动状态。
通过数学建模和推导,可以得到物体质量变化情况下的运动方程,从而更准确地预测物体的运动轨迹和速度。
变质量问题公式

变质量问题公式一、火箭发射类问题。
题目1:一枚火箭的初始质量为M_0,燃料以相对火箭的速度v_e向后喷出。
在某一时刻,火箭的质量变为M,求此时火箭的速度v(假设火箭在太空中,不受外力作用)。
解析:根据变质量物体的动力学方程:M(dv)/(dt)=-v_e(dM)/(dt)分离变量得:dv = - v_e(dM)/(M)两边积分:∫_v_0^v dv=-v_e∫_M_0^M(dM)/(M)其中v_0 = 0(初始速度为0)解得:v = v_eln(M_0)/(M)题目2:火箭的初始质量是1000kg,燃料的喷射速度为2000m/s。
当火箭的质量变为600kg时,它的速度是多少?解析:已知M_0 = 1000kg,M = 600kg,v_e=2000m/s由v = v_eln(M_0)/(M)v = 2000×ln(1000)/(600)=2000×ln(5)/(3)≈ 2000×0.5108 = 1021.6m/s题目3:火箭质量M_0 = 5000kg,燃料喷射速度v_e = 3000m/s。
若要使火箭达到6000m/s 的速度,火箭最终的质量M是多少?解析:根据v = v_eln(M_0)/(M)6000 = 3000×ln(M_0)/(M)ln(M_0)/(M)= 2(M_0)/(M)=e^2M=(M_0)/(e^2)=(5000)/(e^2)≈ 676.7kg二、雨滴增长类问题。
题目4:雨滴在云层中下落时,不断有小水滴凝结在上面。
设雨滴初始质量为m_0,在下落过程中,其质量的增长速率为λ(即(dm)/(dt)=λ),雨滴受到的空气阻力为F = - kv (k为常数,v为雨滴速度)。
求雨滴的速度随时间的变化关系。
解析:根据牛顿第二定律:(m_0+λ t)(dv)/(dt)=(m_0 +λ t)g- kv分离变量得:(dv)/(g-frac{k){m_0+λ t}v}=(dt)/(m_0+λ t)令u = m_0+λ t,则dt=(du)/(λ)方程变为:(dv)/(g-frac{k){u}v}=(du)/(λ u)这是一个一阶线性非齐次微分方程,通过求解该方程可得雨滴速度随时间的变化关系。
理论力学 第二章

dm Fr v r m0 v r (常量) dt vr t s s0 v 0t ln(1 t ) d (1 t )
0
( ln xdx x ln x x c )
s s 0 v 0t
结论:
vr
[(1 t ) ln (1 t ) t ]
3.
dm = 0, 动态平衡。 dt
若 u 0 ,则方程变为:
d (m v ) F dt
4. 若
,则方程变为: u v
dv F m dt
减质型:
m
F
v
m dm
F
u
v dv
dm
由动量定理得:
冲量 末动量
Fdt (m dm)(v dv ) (udm) mv dv 略去高阶小量: dm m F (u v ) dt dt
有:
t
dm t ,则: m0 e dt
dm Fr v r m 0 v r e t v r m dt
Fr ar v r (常 量) 反 作用 力 引起 的 附加 速 度. 加 m 1 2 s s0 v 0 t av r t 2
m′ 更有效于v 的增加, 故采用多级火箭发射(3~ 4级).
vr(
影响燃烧室的温度和压力, 故不能太大) 比增大
2. 求距离
m s s0 v 0 t v r ln dt (喷射行程) 0 m0
t
① 直线率:
dm m m0 m0 t , 则 , m0 (常量) dt
整理得变质量物体的运动微分方程:
§2.7 变质量物体的运动

1 ( Mt t 2 ) g ds (2Mt t 2 ) g (2Mt 2t 2 ) g 2 v dt M t 2( M t ) 2 ( M t ) (2Mt 2t 2 ) g M 2 g M 2 g ( M t )tg Mg ( M t ) M 2 g 2 ( M t ) 2 ( M t ) 1 1M M 2 / 2 gt g g 2 2 M t
将Δm ,m ,视为一质点组,外力矢量和为F,
则由动量定理得:(m m)(v v ) mv mu Ft mv mv mu mv Ft
dv dm m (u v ) F dt dt d (mv ) dm ——米歇尔斯基方程 uF dt dt 3.特例: 1)若u=0,即并入前或放出后的Δm绝对静止,则
§2.7 变质量物体的运动 一、变质量物体的运动方程 1.当物体m(主体物)在运动中,随时间t增长不断地有 质量放出或并入, 称为变质量物体的运动。 一般有m=m(t), 如:喷气式飞机, 火箭,下落的雨滴. 2.运动方程 t时刻,主体物m,v(绝对速度),放出或并入微元质 量为Δm,u
t+Δt时刻,Δm与m合并,Δm +m的速度为v+Δv
d (mv ) F dt dv F 2)若u=v,则 m dt dv dm m 3)对火箭: F (u v ) F Fr dt dt
t 0, mv 0
dm dm dm Fr 源自 (u v ) vr vr | |i dt dt dt
dm 解: dt
积分得, m(t ) M t
u 0, F mg (M t ) g
第9讲 超重、失重
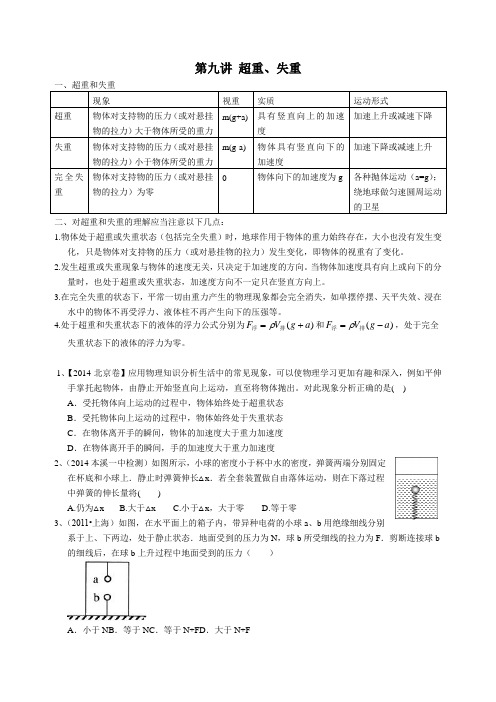
第九讲 超重、失重二、对超重和失重的理解应当注意以下几点: 1.物体处于超重或失重状态(包括完全失重)时,地球作用于物体的重力始终存在,大小也没有发生变化,只是物体对支持物的压力(或对悬挂物的拉力)发生变化,即物体的视重有了变化。
2.发生超重或失重现象与物体的速度无关,只决定于加速度的方向。
当物体加速度具有向上或向下的分量时,也处于超重或失重状态,加速度方向不一定只在竖直方向上。
3.在完全失重的状态下,平常一切由重力产生的物理现象都会完全消失,如单摆停摆、天平失效、浸在水中的物体不再受浮力、液体柱不再产生向下的压强等。
4.处于超重和失重状态下的液体的浮力公式分别为()F V g a ρ=+浮排和()F V g a ρ=-浮排,处于完全失重状态下的液体的浮力为零。
1、【2014·北京卷】应用物理知识分析生活中的常见现象,可以使物理学习更加有趣和深入,例如平伸手掌托起物体,由静止开始竖直向上运动,直至将物体抛出。
对此现象分析正确的是( )A .受托物体向上运动的过程中,物体始终处于超重状态B .受托物体向上运动的过程中,物体始终处于失重状态C .在物体离开手的瞬间,物体的加速度大于重力加速度D .在物体离开手的瞬间,手的加速度大于重力加速度2、(2014本溪一中检测)如图所示,小球的密度小于杯中水的密度,弹簧两端分别固定在杯底和小球上.静止时弹簧伸长△x .若全套装置做自由落体运动,则在下落过程中弹簧的伸长量将( )A.仍为△xB.大于△xC.小于△x ,大于零D.等于零3、(2011•上海)如图,在水平面上的箱子内,带异种电荷的小球a 、b 用绝缘细线分别系于上、下两边,处于静止状态.地面受到的压力为N ,球b 所受细线的拉力为F .剪断连接球b 的细线后,在球b 上升过程中地面受到的压力( )A .小于NB .等于NC .等于N+FD .大于N+F4、(2014河北唐山模拟)如图所示,顶角为直角、质量为M的斜面体abc放在粗糙的水平面上。
变质量物体的运动

dm (m v) u F , ( m m (t ) ) dt dt d
F
m
t 时刻
但此时:
t t 时刻
m m ( t );
讨论: (1)
(2)
v u
dm dt
时 :m
dv dt
F,
可正,可负,合‘ + ’,离‘ - ’ .
例:P.137. 由题意:
m0 m
m ms
)
m’ 更有效于v 的增加, 故采用多级火箭发射(3~ 4级).
vr(
影响燃烧室的温度和压力, 故不能太大) 比增大
2. 喷射行程
m0 ① m 为直线率: m m 0 m 0 t vr t s s0 v 0t ln ( 1 t ) d ( 1 t )
d
dm d dm (m v) u F, m v F (u v) dt d力: Fr
m 0 v r ( 常量 ) Fr v r
m ② 指数率: m 0 e
t
, 则 :s s0 v 0 t
0
s s0 v 0 t v r
t
ln
m
dt
0
( ln xdx x ln x x c )
s s0 v 0t
vr
[( 1 t ) ln ( 1 t ) t ]
* m 为直线率说明反冲力是常量. dm m m 0 m 0 t , 则, m 0 ( 常量 ) dt
1 2
v rt
2
* m 为指数率说明反冲力引起的附加加速度是常量.
Fr v r dm dt m 0 v r e
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九讲 变质量物体的运动
教学时间:2学时
教学目的要求:
使学生熟练掌握变质量物体的运动微分方程——密舍尔斯基方程并能解决实际问题。
重点:密舍尔斯基方程的应用。
难点:如何判断对具体问题使用哪种密舍尔斯基方程。
教学方法:数学推导结合典型实例分析。
讲授要点及内容:
日常生活和生产实践中,我们经常见到物体在运动过程中其质量不断发生变化,例如: 喷气飞机、火箭、洒水车、下落的雨点等等。
定义:若物体在运动过程中,其质量随时间不断变化,则物体的这种运动称为变质量物体 的运动。
说明:1)本节只研究物体运动时,其质量按一定规律变化的情况。
2)本节所研究的变质量物体可视为质点。
3)本节研究物体的质量随时间变化,与相对论中物体的质量随速度变化就有本质 的不同。
(一)对变质量物体运动的初步分析
1、基本概念
主体——质量随时间不断变化的运动物体(如飞机、雨滴)。
并体(分体)——在dt 时间内合并到主体上或从主体上分出的微质量物体。
2、问题的实质——将主体和并体(或分体)均视为质点并且由于合并(分开)瞬时它们之 间存在相互作用力,因此问题的实质应为质点组动力学问题。
3、研究问题的着眼点——质量不断发生变化的主体的运动规律应是研究问题的着眼点,因 此这类问题又可视为主体的质点动力学问题。
4、研究问题的方法——从质点的动力学基本定理出发,最后归结为主体的运动微分方程。
(二)变质量物体的运动微分方程(以质量不断增加为例)
设:1)t 时刻,主体质量为m ,相对于某惯性系的绝对速度是v r ,并体质量为dm ,相对于
同一惯性系的绝对速度为u r 。
2)在dt 时间内主体与并体完成合并。
3)在t dt + 时刻,主体的质量变为m dm + ,相对于同一惯性系的速度为v dv + r r。
4)在dt 时间内,作用在和的外力主矢量为F u r 。
根据质点组动量定理( )( ) ( )
m dm v dv mv udm Fdt ++-+= r r r r u r , 将该式展开并略去二阶无穷小量dmdv r
,得 ( ) d dm mv u F dt dt -= r r u r (1), ( ) dv dm m F v u dt dt =+- r u r r r (2) 可进一步将方程整理成两种形式
(1)(2)两式均称为密舍尔斯基方程,使解决变质量物体运动的重要动力学方程。
说明:
1)该方程虽然是从主体质量不断增加导出的,但同样适用于主体不断减小的情况。
0 0 dm dt > ì í < î
主体质量增加。
——主体质量的时间变化率 主体质量减少。
2)方程(2)可视为主体运动微分方程。
其中, dv dt
r ——主体加速度。
m ——主体质量。
( )
dm v u dt
- r r ——微质量对主体的反作用力。
(喷气飞机就是靠此力向前飞行)。
讨论:1)若u v = r r 的关系可以通过其他方程很方便的求出,则一般采用方程(2)求解。
2)若v r 与t 的关系很难通过其他方程求出,则一般采用方程(1)求解。
3)两种特殊情况
若 0 u = r ,则由方程(1)得 ( )
d mv F dt
= r u r 若u v = r r ,则由方程(2)得 dv m F dt = r ur 这两个方程与质点的运动微分方程的形式完全相同,但不是恒质量,而是随时间变化的,因 此不能随意从微商号移出、移进。
作业:214,216。
