333点到直线距离
点到直线的距离教学设计

课题:点到直线的距离 教学目标:1、知识与技能:(1)熟记点到直线的距离公式,了解公式的推导过程; (2)理解两平行线之间距离公式的推导方法,会求两平行线之间的距离;(3)能灵活应用点到直线的距离公式来解决一些简单的实际问题。
2、过程与方法:本节课主要通过讲练结合以练为主的方法进行教学。
3、情感态度与价值观:通过引导学生了解点到直线的距离公式的求解步骤和推导两平行线之间的距离公式,渗透由特殊到一般,由一般到特殊的数学思想,培养学生形成严谨的科学态度。
教学重难点:重点:点到直线的距离公式及应用。
难点:灵活应用点到直线的距离公式解决实际问题。
课时安排:1课时教学过程知识回顾:1、 两点),(111y x p ,),(222y x p 间的距离公式是什么?22122121)()(y y x x P P -+-=2、已知两点的坐标,如何求过这两点的直线方程?先根据已知两点的坐标,求出过这两点的直线的斜率,再根据点斜式求出直线的方程。
3、直线的一般式方程的形式?0=++C By Ax (其中A 、B 不全为零)导入新课:在平面直角坐标系中,如何求出一个已知点),(00y x P 到一条已知直线0:=++C By Ax l (其中A 、B 不全为零)的距离呢?这就是我们本节课要探究的内容。
新知探究1:我们知道求点P 到直线l 的距离,先要过点P 作直线l 的垂线PH ,垂足为H ,再求出垂线段PH 的长度,这就是点P 到直线l 的距离。
所以在平面直角坐标系中求点),(00y x P 到直线0:=++C By Ax l (其中A 、B第一步:确定直线l的斜率k = -BA第二步:求与l 垂直的直线l '的斜率k ='第三步:运用点斜式求过点P 垂直于l 直线l '的方程第四步:联立两直线方程,求l 与l '第五步:用两点间距离公式求点P 与点H 的距离第六步:得到点P 到l 的距离PH d =有兴趣的同学,下去以后可以按照上面步骤自己求一下。
高一数学必修二两条平行线间的距离公式

择恰当的点,最好选 择坐标为整数的点。
l1: 2x-7y-8=0
3、利用点到直线的距离公式求解。
应用新知
求下列两条平行直线间的距离:
(1)2x+3y-8=0
2x+3y+18=0
d | 2 4 7 0 18 | 26 13 2 13
22 32
13
(2)3x+4y=10
3x+4y=0
点到直线的距离
P0(x0,y0)到直线l:Ax+By+C=0的距离:
d | Ax0 By0 C | A2 B2
练习
d |12 (5) 5 7 3 | 22
12、. 求求点点BA((-d-52,,d73|))3到到|2直直(线2线2121322(2)x2x1+1+)24554y21y+0+|333==7005的3的51|3距距离离9..
22 (7)2
53
所以平行线l1与l2的距离为
12 53 53
应用新知
例1、已知直线l1:2x-7y-8=0与l2:6x-21y-1=0试
判断l1与l2平行吗?若平行,求l1与l2的距
离。
y
分析:
l2:6x-21y-1=0
Байду номын сангаас
1、判断两线平行应 分别求出它们的斜率。 2、在一条直线上选 o
d
x
A
16
距离是_____1_3 ;
2.两平行线3x-2y-1=0和6x-4y+2=0的 距离是___2_1.313
作业: 必做题:教材 P110 9、10 选做题: 教材P110 B组 9
333点到直线的距离公式

即C=-Ax0-By0.
所以Ax1+By1+C=Ax1+By1-Ax0-By0,
即A(x1-x0)+B(y1-y0)=Ax1+By1+C.②
把等式①和②两边平方后相加,整理可得
(A2+B2)[(x1-x0)2+(y1-y0)2]=(Ax1+By1+C)2,
故要完成任务,至少需要9km长的电线.
(2)设直线l:3x-4y-10=0与x轴的交点为Q,则Q( ,0).在直线l上任取一点M(0,- ),易让向量 =( , )与向量n=(3,-4)垂直.
设向量 与向量n的夹角为θ,点P到直线l的距离为d,由向量的数量积的定义易知
(3)设过点P(15,20)与l:3x-4y-10=0垂直的直线为m,易求m的方程为4(x-15)+3(y-20)=0.
25[(xo-15)2+(yo-20)2]=452,
∴(xo-15)2+(yo-20)2= ,
3.教师展现学生们的求法,师生共同点评各种求法,得出:求垂线与直线的交点坐标,再用两点间的距离公式使问题得解,想法虽自然,但计算量较大;不求垂足的坐标,设出垂足的坐标代入直线方程,进而通过等式变形,利用两点间的距离公式求得结果,想法既巧妙,又简单明了.
即(x1-x0)2+(y1-y0)2=
容易看出,等式左边即为点P(x1,y1)到直线l距离的平方.由此我们可以得到点P(x1,y1)到直线l的距离d的计算公式:
归纳求点P(x1,y1)到直线l:Ax+By+C=0的距离的计算步骤如下:
(1)给出点的坐标x1和y1赋值.
(2)给A,B,C赋值.
(3)计算
设垂足为Po(xo,yo),则4(xo-15)+3(yo-20)=0,①
(北师大版)石家庄市高中数学选修4-4第二章《参数方程》测试(答案解析)

一、选择题1.点(, )A x y 是曲线2cos 13sin x y θθ=+⎧⎨=+⎩,(θ为参数)上的任意一点,则2 -x y 的最大值为( ) AB5C .3D3+2.已知直线l的参数方程为22x m t y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为2222cos 3sin 12ρθρθ+=,且曲线C 的左焦点F 在直线l 上,若直线l 与曲线C 交于A 、B 两点,则FA FB ⋅的值等于( ) A .1BCD .23.在直角坐标系xOy 中,以O 为极点,x 轴正半轴为极轴,建立极坐标系,直线l 的参数方程为1cos sin x t y t αα=-+⎧⎨=⎩,(t 为参数),曲线C 的方程为4cos 02πρθθ⎛⎫= ⎪⎝⎭,(2,0)C 直线l 与曲线C 相交于A B ,两点,当ABC ∆的面积最大时,tan α=( )A.3B.2CD .74.在参数方程cos sin x a t y b t θθ=+⎧⎨=+⎩,(0θπ<,t 为参数)所表示的曲线上有,B C 两点,它们对应的参数值分别为1t ,2t ,则线段BC 的中点M 对应的参数值是( ) A .122t t - B .122t t + C .122t t - D .122t t + 5.直线122x ty t=+⎧⎨=+⎩(t 是参数)被圆229x y +=截得的弦长等于( )A.125BCD 6.已知在平面直角坐标系xoy 中,曲线C 的参数方程为 4cos ()sin x y 为参数ααα=⎧⎨=⎩,M 是曲线C 上的动点.以原点O 为极点,x 轴的正半轴为极轴,取相同的长度单位建立极坐标系,若曲线T 的极坐标方程为2sin cos 20ρθρθ+=,则点M 到点T 的距离的最大值为( )A.2+BC.4+D.7.直线4x 1t 5(t 3y 1t5⎧=+⎪⎪⎨⎪=-+⎪⎩为参数)被曲线πρθ4⎛⎫=+ ⎪⎝⎭所截的弦长为( ) A .15B .710C .75D .578.已知直线l的参数方程为112x y t ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数),直线l 与圆2216x y +=相交于A ,B 两点,则线段AB 的中点坐标为( ) A .(3,3)- B.3)-C.(D.3(,9.直线21{(1x t t y t =-=+为参数) 被圆229x y +=截得的弦长等于( )A .125B.5C.5D.510.动点1293cos 4sin 1,cos sin 2(55M θθθθθ⎛⎫--++ ⎪⎝⎭为参数)的轨迹的普通方程为( )A .22(1)(2)1259x y +-+=B .22(1)(2)1259x y -++=C .22(1)(2)1925x y +-+=D .22(1)(2)1925x y -++=11.若动点(,)x y 在曲线2221(0)4x yb b+=>上变化,则22x y +的最大值为( )A .24(04)42(4)b b b b ⎧+<⎪⎨⎪>⎩B .24(02)42(4)b b b b ⎧+<<⎪⎨⎪⎩C .244b +D .2b12.设椭圆C :2211612x y +=上的一点P 到两条直线4y =和8x =的距离分别是1d ,2d ,则122d d +的最小值( ) A .5B .6C .7D .8二、填空题13.已知曲线C参数方程为22cos2sinxyθθ=+⎧⎨=⎩(θ为参数),直线l方程为:x y-+=,将曲线C横坐标缩短为原来的12,再向左平移1个单位,得到曲线1C,则曲线1C上的点到直线l距离的最小值为______.14.曲线C的参数方程为4cossinxyαα=⎧⎨=⎩(α为参数),M是曲线C上的动点,若曲线T 极坐标方程2sin cos20ρθρθ+=,则点M到T的距离的最大值为__________.15.直线415{315x ty t=+=--(t为参数)被曲线4πρθ⎛⎫=+⎪⎝⎭所截得的弦长为 . 16.已知曲线C:2cossinxyθθ=⎧⎨=⎩(θ为参数).若点P在曲线C上运动,点Q为直线:0l x y+=-上的动点,则PQ的最小值为________.17.直线122x ty⎧=+⎪⎪⎨⎪=⎪⎩(t为参数)被双曲线221x y-=截得的弦长为_________.18.已知在极坐标系中,曲线C的极坐标方程是2sin4cos0ρθθ+=,以极点为原点,极轴为x轴的正半轴建立直角坐标系,直线l的参数方程是112x tty⎧=-+⎪⎪⎨⎪=⎪⎩(为参数),M (0l与曲线C的公共点为P,Q,则11PM QM+=_______19.已知(,)P x y是椭圆22143x y+=上的一个动点,则x y+的最大值是__________.20.在直角坐标系xOy中,以O为极点,x轴正半轴为极轴,建立极坐标系,直线l的参数方程为1cos,sinx ty tαα=-+⎧⎨=⎩(t为参数),曲线C的方程为4cosρθ=(02πθ≤≤),()2,0C.直线l与曲线C相交于A,B两点,当ABC的面积最大时,tanα=______.三、解答题21.已知直线l的参数方程为12{2x ty ==(t 为参数),曲线C 的参数方程为4cos {4sin x y θθ==(θ为参数).(1)将曲线C 的参数方程化为普通方程;(2)若直线l 与曲线C 交于,A B 两点,求线段AB 的长. 22.[选修4-4:坐标系与参数方程]在平面直角坐标系xOy 中,曲线1C 的参数方程为22cos 2sin x ty t =+⎧⎨=⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,并使得它与直角坐标系有相同的长度单位,曲线2C 的极坐标方程为2sin ρθ=,曲线3C 的极坐标方程为(0)6πθρ=>. (1)求曲线1C 的普通方程和3C 的直角坐标方程; (2)设3C 分别交1C 、2C 于点P 、Q ,求1C PQ ∆的面积.23.已知直线l的参数方程为12x y ⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数).在平面直角坐标系xOy 中,()1,2P ,以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线M 的极坐标方程为4cos ρθ=,直线l 与曲线M 交于A ,B 两点. (1)求曲线M 的直角坐标方程; (2)求PA PB ⋅的值.24.在平面直角坐标系xoy 中,已知直线l的参数方程为42x t y ⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数),以直角坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为413cos 4k k k k ρπθ=⎛⎫-++ ⎪⎝⎭.(1)当1k =时,求直线l 和C 的普通方程;(2)当2k =时,试判断直线l 和C 有无交点若有,求出交点的坐标;若无,说明理由.25.在直角坐标系xOy 中直线l的参数方程为1x y ⎧=-⎪⎪⎨⎪=⎪⎩(t 为参数),以O 为极点,x 轴的非负半轴为极轴建立极坐标系,曲线C 的极坐标方程为2cos 2sin ρθθ=. (1)求直线l 的普通方程和曲线C 的直角坐标方程; (2)若直线l 交曲线C 于A ,B 两点,求线段AB 的长度.26.在直角坐标系xOy 中,直线l的参数方程为32t x y ⎧=-+⎪⎪⎨⎪=⎪⎩.(t 为参数).以坐标原点O为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为24cos 30p ρθ-+=.(1)求l 的普通方程及C 的直角坐标方程; (2)求曲线C 上的点P 到l 距离的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】利用曲线的参数方程得32co sin -32s x y θθ=+-化简求解即可 【详解】由题()32cos 3sin 23-s x y θθθϕ=+-=++ 故当()cos 1θϕ+=时,2 -x y3+ 故选D 【点睛】本题考查参数方程求最值,考查辅助角公式,是基础题2.D解析:D 【分析】根据题意,将曲线C 的极坐标方程变形为标准方程,由直线过的点的坐标可得m 的值,将直线的参数方程与曲线C 的方程联立,可得2220t t --=,由一元二次方程根与系数的关系计算可得答案;【详解】解:根据题意,曲线C 的极坐标方程为2222cos 3sin 12ρθρθ+=,则其标准方程为221124x y +=,其左焦点为(-,直线l过点(-,其参数方程为(x m ty ⎧=⎪⎪⎨⎪=⎪⎩为参数),则m =-将直线l的参数方程22x y ⎧=-⎪⎪⎨⎪=⎪⎩与曲线C 的方程221124x y +=联立,得2220t t --=, 则12||||||2FA FB t t ==. 故选:D 【点睛】本题考查椭圆的极坐标方程、参数方程,涉及椭圆与直线的位置关系,关键是求出椭圆、直线的普通方程,属于中档题.3.D解析:D 【分析】先将直线直线l 与曲线C 转化为普通方程,结合图形分析可得,要使ABC ∆的面积最大,即要ACB ∠为直角,从而求解出tan α. 【详解】解:因为曲线C 的方程为4cos 02πρθθ⎛⎫= ⎪⎝⎭, 两边同时乘以ρ,可得24cos ρρθ=,所以曲线C 的普通方程为22(2)4(02)x y y -+=, 曲线C 是以(2,0)C 为圆心,2为半径的上半个圆. 因为直线l 的参数方程为1cos sin x t y t αα=-+⎧⎨=⎩,(t 为参数),所以直线l 的普通方程为tan tan 0x y αα-+=,因为1sin 2sin 2ABCS CA CB ACB ACB ∆, 所以当ACB ∠为直角时ABC ∆的面积最大,此时C 到直线l 的距离22222AB CA CB d +=== ,因为直线l 与x 轴交于()1,0D -, 所以3CD =,于是7DE =, 所以214tan 77α==, 故选D . 【点睛】本题考查了曲线的参数方程、极坐标方程与普通方程之间的互化,同时考查了直线与圆的位置关系,数形结合是本题的核心思想.4.D解析:D 【解析】 【分析】根据参数的几何意义求解即可。
坐标轴点到直线距离公式

坐标轴点到直线距离公式
在数学中,我们常常遇到需要计算坐标轴上某点与直线之间的距离的情况。
为了解决这个问题,我们可以使用坐标轴点到直线的距离公式。
在直角坐标系中,一条直线可以由方程表示,例如直线的方程为y = mx + c,其中m为直线的斜率,c为直线经过y轴的截距。
给定一个坐标轴上的点P(x, y),我们可以利用以下公式计算点P 到直线的距离。
距离D = |y - mx -c| / √(1 + m^2)
其中,|*|表示绝对值函数,√表示平方根。
举个例子来说明。
假设我们需要计算点P(3, 4)到直线y = 2x + 1的距离,我们可以将坐标值代入公式中进行计算。
将直线的斜率m = 2和截距c = 1带入公式得到:
距离D = |4 - 2(3) - 1| / √(1 + 2^2) = |4 - 6 - 1| / √(1 + 4) = |-3| / √5 = 3 / √5
所以,点P(3, 4)到直线y = 2x + 1的距离为3 / √5。
通过使用坐标轴点到直线距离公式,我们可以准确计算出任意给定坐标轴上的点到直线的距离。
这个公式在几何学和物理学中都有广泛的应用,可以帮助我们更好地理解和解决问题。
课时作业3:2.3.3 点到直线的距离公式 ~2.3.4 两条平行直线间的距离

2.3.3 点到直线的距离公式 ~2.3.4 两条平行直线间的距离(建议用时:40分钟)一、选择题1.动点P 在直线x +y -4=0上,O 为原点,则|OP |的最小值为( ) A .10 B .22 C .6D .22.已知两条直线l 1:2x +y -1=0,l 2:4x +2y +2=0,则l 1,l 2的距离为( ) A .255 B .355 C .5D .253.已知点P (1+t,1+3t )到直线l :y =2x -1的距离为55,则点P 的坐标为( ) A .(0,-2) B .(2,4) C .(0,-2)或(2,4)D .(1,1)4.与直线x +y =0平行,且它们之间的距离为2的直线方程为( ) A .x +y +2=0 B .x -y +2=0C .x +y +2=0或x +y -2=0D .x +y +1=0或x +y -1=05.在平面直角坐标系中,点A (1,2),点B (3,1)到直线l 的距离分别为1和2,则符合条件的直线条数为( ) A .3 B .2 C .4 D .1二、填空题6.△ABC 的三个顶点的坐标分别为A (2,1),B (3,4),C (-2,-1),则△ABC 的面积为________.7.已知直线3x +4y -3=0与6x +my +14=0相互平行,则它们之间的距离是________.8.P,Q分别为直线3x+4y-12=0与6x+8y+6=0上任意一点,则|PQ|的最小值为________.三、解答题9.已知直线l的斜率为-34,且直线l经过直线kx-y+2k+5=0所过的定点P.(1)求直线l的方程;(2)若直线m平行于直线l,且点P到直线m的距离为3,求直线m的方程.10.如图,已知直线l1:x+y-1=0,现将直线l1向上平移到直线l2的位置,若l2,l1和坐标轴围成的梯形面积为4,求l2的方程.11.(多选题)两条平行线分别经过点A(6,2),B(-3,-1),下列可能是这两条平行线间的距离的是()A.4B.7C.9D.1112.(多选题)下列过(2,2)的直线l中,到两点A(0,-2),B(8,2)的距离相等的是()A.x+y-4=0B.x=2C.2x+y-6=0D.x-2y+2=013.(一题两空)已知直线l经过直线2x+y-5=0与x-2y=0的交点P,若点A(5,0)到直线l的距离为3,则直线l的方程为________,点A(5,0)到直线l的距离的最大值是________.14.若两平行直线3x-2y-1=0和6x+ay+c=0之间的距离是21313,则c+2a的值为________.15.已知点A(3,1),在直线y=x和y=0上各找一点M和N,使△AMN的周长最短,并求出最短周长.参考答案一、选择题 1.B【解析】原点O 到直线x +y -4=0的距离为d ,由点到直线距离的性质知d =|OP |min ,因此,|OP |min =|0+0-4|12+12=22,故选B. 2.A【解析】因为两直线l 1:2x +y -1=0,l 2:4x +2y +2=0平行,则它们之间的距离即为l 1:2x +y -1=0与l 2:4x +2y +2=0之间的距离为:d =|-2-2|16+4=425=255.3.C【解析】直线l :y =2x -1可化为2x -y -1=0,依题意得|2(1+t )-(1+3t )-1|22+(-1)2=55,整理得|t |=1,所以t =1或-1.当t =1时,点P 的坐标为(2,4);当t =-1时,点P 的坐标为(0,-2),故选C. 4.C【解析】依题意设所求直线方程为x +y +c =0(c ≠0),则|c -0|12+12=2⇒|c |=2,故c =±2.因此所求直线方程为x +y ±2=0,故选C.5.B 【解析】由点A (1,2),点B (3,1)可得|AB |=4+1=5<1+2,所以不存在与线段AB 相交的符合题意的直线,故存在两条符合题意的直线,这两条直线在线段AB 的两侧,如图,故选B. 二、填空题 6. 5【解析】由两点式得AB 的直线方程为y -14-1=x -23-2,即3x -y -5=0.再由点到直线距离公式得点C 到直线AB 的距离为d =|-6+1-5|32+(-1)2=10.又|AB |=(3-2)2+(4-1)2=10.∴S △ABC =12×10×10=5. 7. 2【解析】因为直线3x +4y -3=0与6x +my +14=0平行,所以3m -4×6=0, 解得m =8,所以6x +my +14=0,即是3x +4y +7=0, 由两条平行线间的距离公式可得d =|7+3|32+42=2. 8.3【解析】直线6x +8y +6=0可变形为3x +4y +3=0,由此可知两条直线平行,它们的距离d =|-12-3|32+42=3,∴|PQ |min =3. 三、解答题9.[解] (1)kx -y +2k +5=0,即k (x +2)+(5-y )=0,所以过定点P (-2,5),又直线l 的斜率为-34.因此其方程为y -5=-34(x +2),即l :3x +4y -14=0.(2)设直线m :y =-34x +b ,则3=⎪⎪⎪⎪⎪⎪34×(-2)+5-b 916+1⇒b =-14或294.∴直线m 为:y =-34x -14,或y =-34x +294. 10. [解] 设l 2的方程为y =-x +b (b >1), 则A (1,0),D (0,1),B (b,0),C (0,b ), ∴|AD |=2,|BC |=2b .梯形的高h 就是A 点到直线l 2的距离, 故h =|1+0-b |2=|b -1|2=b -12(b >1),由梯形面积公式得2+2b 2×b -12=4,∴b 2=9,b =±3.但b >1, ∴b =3.从而得到直线l 2的方程是x +y -3=0.11.ABC【解析】当两直线的斜率不存在时,两直线方程分别为x =6,x =-3,则d =9. 当两直线的斜率存在时,设两直线方程分别为y -2=k (x -6)与y +1=k (x +3), 即kx -y +2-6k =0,kx -y +3k -1=0, ∴d =|2-6k -3k +1|k 2+1=|9k -3|k 2+1.由此可得(81-d 2)k 2-54k +9-d 2=0.当81-d 2=0,即d =9时,k =-43,∴d =9成立.当d ≠9时,由k ∈R ,可得Δ=(-54)2-4(81-d 2)(9-d 2)≥0, 即d 4-90d 2≤0,∴0<d ≤310且d ≠9. 综上所述,d ∈(0,310].故应选ABC.12.AD 【解析】显然斜率不存在时x =2不合适,设l :y -2=k (x -2)即kx -y +2-2k =0,由条件可知|4-2k |k 2+1=|6k |k 2+1,解得k =12或-1.当k =12时,l ∥AB ,方程为x -2y +2=0,当k =-1时,l 过AB 中点,方程为x +y -4=0.13.4x -3y -5=0或x =210【解析】经过两已知直线交点的直线方程为(2x +y -5)+λ(x -2y )=0,即(2+λ)x +(1-2λ)y -5=0, ∴|5(2+λ)-5|(2+λ)2+(1-2λ)2=3, 即2λ2-5λ+2=0, 解得λ=2或12,∴l 的方程为4x -3y -5=0或x =2. 由⎩⎨⎧2x +y -5=0,x -2y =0, 解得交点P (2,1),过点P 任意作直线l (图略),设d 为点A 到l 的距离,则d ≤|P A |(当l ⊥P A 时等号成立),∴d max =|P A |=10. 14.±1【解析】由两平行直线得3a +12=0,解得a =-4.方程3x -2y -1=0可化为6x -4y -2=0,利用平行线间的距离公式得|c +2|62+42=21313,解得|c +2|=4,所以c +2a =±4-4=±1.15.[解] 由点A (3,1)及直线y =x ,可求得点A 关于直线y =x 的对称点为B (1,3),同样可求得点A 关于直线y =0的对称点为C (3,-1),如图所示.则|AM |+|AN |+|MN |=|BM |+|CN |+|MN |≥|BC |=25,当且仅当B ,M ,N ,C 四点共线时,△AMN 的周长最短,为2 5.由B (1,3),C (3,-1) 可得直线BC 的方程为2x +y -5=0.由⎩⎨⎧2x +y -5=0,y =x得⎩⎪⎨⎪⎧x =53,y =53,故M 点的坐标为⎝ ⎛⎭⎪⎫53,53.对于2x +y -5=0,令y =0,得x =52,故N 点的坐标为⎝ ⎛⎭⎪⎫52,0.故在直线y =x 上找一点M ⎝ ⎛⎭⎪⎫53,53,在直线y =0上找一点N ⎝ ⎛⎭⎪⎫52,0,可使△AMN的周长最短,为2 5.。
333点到直线、两平行线间的距离

两条平行直线间的距离是指夹在两条平行直
线间的公垂线段的长.
y
P l1
d C1 - C2 A2 B2
l2
Q
o
x
例7、求证:两条平行线l1:Ax+By+C1=0与
l2: Ax+By+C2=0的距离是
d
ቤተ መጻሕፍቲ ባይዱ
C1 - C2
A2 B2
例7、求证:两条平行线l1:Ax+By+C1=0与
l2: Ax+By+C2=0的距离是 d C1 - C2
§3.3. 3 点到直线的距离
两点间的距离公式是什么?
已知平面上两点P1(x1,y1), P2(x2,y2),如何 求P1 P2的距离| P1 P2 |呢?
y P1(x1,y1) Q(x2,y1)
P2(x2,y2)
o
x
| P1P2 | (x2 x1)2 ( y2 y1)2
特别地,原点O与任一点P(x, y)的距离:
y
A2 B2
P
l1 证明:B l2
0时,在l1上取一点P
0,-
C1 B
,
o
Q
x
则P到l2的距离d
A
0
B
C1 B
C2
A2 B2
注意:两直线方程的 A,B应相同
C1 C2 A2 B2
B 0时,则A 0,同理可证它们之间的距离为 d C1 C2
A2 B2
练习2
14 53
1.平行线2x-7y+8=0和2x-7y-6=0的距离是___5_3__;
d RS PR • PS PR • PS
d RS
d Ax0 By0 C A2 B2
2.3.3 点到直线的距离公式~2.3.4 两条平行直线间的距离(解析版)..
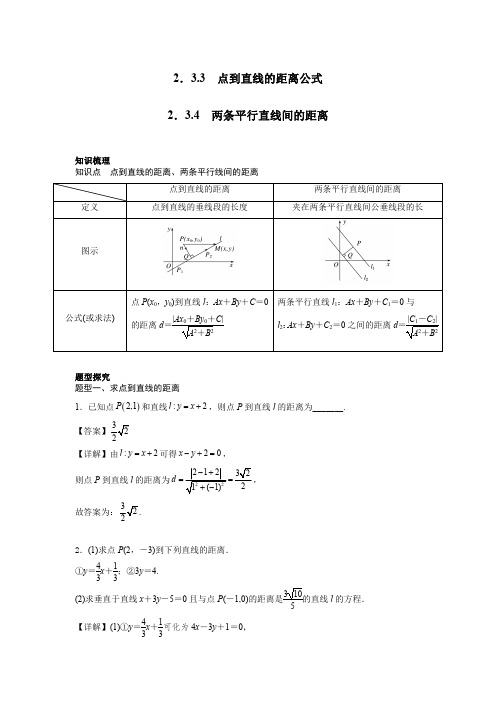
2.3.3点到直线的距离公式2.3.4两条平行直线间的距离知识梳理知识点点到直线的距离、两条平行线间的距离点到直线的距离两条平行直线间的距离定义点到直线的垂线段的长度夹在两条平行直线间公垂线段的长图示公式(或求法)点P (x 0,y 0)到直线l :Ax +By +C =0的距离d =|Ax 0+By 0+C |A 2+B 2两条平行直线l 1:Ax +By +C 1=0与l 2:Ax +By +C 2=0之间的距离d =|C 1-C 2|A 2+B 2题型探究题型一、求点到直线的距离1.已知点()2,1P 和直线:2l y x =+,则点P 到直线l 的距离为_______.【答案】322【详解】由:2l y x =+可得20x y -+=,则点P 到直线l 的距离为222123221(1)d -+==+-,故答案为:322.2.(1)求点P (2,-3)到下列直线的距离.①y =43x +13;②3y =4.(2)求垂直于直线x +3y -5=0且与点P (-1,0)的距离是3105的直线l 的方程.【详解】(1)①y =43x +13可化为4x -3y +1=0,则点P (2,-3)到该直线的距离为|4×2-3×(-3)+1|42+(-3)2=185.②3y =4可化为3y -4=0,则点P (2,-3)到该直线的距离为|-3×3-4|02+32=133.(2)设与直线x +3y -5=0垂直的直线的方程为3x -y +m =0,则由点到直线的距离公式知,d =|3×(-1)-0+m |32+(-1)2=|m -3|10=3105.所以|m -3|=6,即m -3=±6.得m =9或m =-3,故所求直线l 的方程为3x -y +9=0或3x -y -3=0.题型二、由点到直线的距离求参数或范围1.已知(2,0),(4,)-A B a 两点到直线:3410l x y -+=的距离相等,则=a ()A .2B .92C .2或8-D .2或92【答案】D【详解】因为(2,0),(4,)-A B a 两点到直线:3410l x y -+=的距离相等,所以有22223(2)0(4)13441134523(4)3(4)a a a ⨯-+⨯-+⨯-+=⇒-=⇒=+-+-,或92a =,故选:D2.已知直线():22l y k x =-+,当k 变化时,点()1,2P -到直线l 的距离的取值范围是()A .[)0,∞+B .[]0,2C .[]0,3D .[)0,3【答案】D【详解】由题意知直线():22l y k x =-+过定点()2,2A ,且不与x 轴垂直,当直线():22l y k x =-+经过点()1,2P -时,,点()1,2P -到直线l 的距离最小为0,当过点()2,2A 的直线垂直于x 轴时,点()1,2P -到该直线的距离最大,最大值为3,如图示:由于():22l y k x =-+的斜率存在,故点()1,2P -到直线l 的距离小于3,即点()1,2P -到直线l 的距离的取值范围是[)0,3,故选:D.3.已知点()M a b ,在直线34200x y +-=上,则22a b +的最小值为_____.【答案】4【详解】根据题意知,22a b +表示原点到直线34200x y +-=上的点的距离,∴22a b +大于等于原点到直线34200x y +-=的距离,原点到直线34200x y +-=的距离为2045=,∴224a b + ,∴22a b +的最小值为4.故答案为:4.题型三、两平行线间的距离1.直线120l x y ++=:与直线22210l x y +-=:之间的距离为_________.【答案】524【详解】因为直线120l x y ++=:与直线22210l x y +-=:平行,而直线22210l x y +-=:可化为2102l x y +-=:,故直线120l x y ++=:与直线22210l x y +-=:之间的距离为1|2()|52242d --==,故答案为:5242.两条平行直线34120x y +-=与8110ax y ++=之间的距离为()A .235B .2310C .72D .27【答案】C【详解】因为直线34120x y +-=与直线8110ax y ++=平行,所以8113412a =≠-,解得6a =,将68110x y ++=化为113402x y ++=,所以两平行直线34120x y +-=与113402x y ++=之间的距离为2211|12|72234--=+.故选:C3.若直线230x y +-=与直线420++=x y a 之间的距离不大于5,则实数a 的取值范围为()A .4a ≤B .164a -≤≤C .416a -≤≤D .16a ≤或4a ≥【答案】B【详解】直线230x y +-=化为4260x y +-=,则两直线之间的距离226542a d +=≤+,即610a +≤,解得164a -≤≤.所以实数a 的取值范围为164a -≤≤.故选:B.4.过点(1,0)A 的直线1l 与过点(1,4)B -的直线2l 平行,且它们之间的距离为2,求直线1l 和2l 的方程.【答案】1:10l x y +-=,2:30l x y +-=;或1:770l x y +-=,2:730l x y ++=【详解】当两直线的斜率不存在时,方程分别为1x =,1x =-,此时它们之间的距离为2,不满足题意;当两直线的斜率存在时,设方程分别为(1)y k x =-与()14=++y k x ,即kx y k 0--=,40kx y k -++=.它们之间的距离为2,22421+∴=+k k ,化简得287=0++k k ,解得1k =-,或7k =-,∴这两条直线的方程为1:10l x y +-=,2:30l x y +-=;或1:770l x y +-=,2:730l x y ++=题型四、距离的综合应用1.两条互相平行的直线分别过点A (6,2)和B (-3,-1),并且各自绕着A ,B 旋转,如果两条平行直线间的距离为d .求:(1)d 的变化范围;(2)当d 取最大值时,两条直线的方程.【详解】(1)如图,显然有0<d ≤|AB |.而|AB |=(6+3)2+(2+1)2=310.故所求的d 的变化范围为(0,310].(2)由图可知,当d 取最大值时,两直线与AB 垂直.而k AB =2-(-1)6-(-3)=13,所以所求直线的斜率为-3.故所求的直线方程分别为y -2=-3(x -6)和y +1=-3(x +3),即3x +y -20=0和3x +y +10=0.2.已知△ABC 的顶点坐标为A (1,1),B (m ,m ),C (4,2),1<m <4.当m 为何值时,△ABC 的面积S 最大?【详解】|AC |=(4-1)2+(2-1)2=10,直线AC 的方程为y -12-1=x -14-1,即x -3y +2=0.因为点B (m ,m )到直线AC 的距离d =|m -3m +2|12+(-3)2,所以△ABC 的面积S =12|AC |·d =12|m -3m +2|=12|m -322-14|.因为1<m <4,所以1<m <2,所以0<|m -322-14|≤14,0<S ≤18.所以当m =32,即m =94时,△ABC 的面积S 最大.跟踪训练1.点(1,2)到直线:3450l x y ++=的距离为___.【答案】165【详解】由点线距离公式有(1,2)到直线:3450l x y ++=的距离为22|31425|16534⨯+⨯+=+.故答案为:1652.在第一象限的点()1,A a 到直线4310x y +-=的距离为3,则a 的值为__________.【答案】4【详解】()1,A a 在一象限,所以0a >,点()1,A a 到直线4310x y +-=的距离为3,则43135a +-=,解得:4a =或6a =-.因为0a >,所以4a =.故答案为:4.3.在平面角坐标系xOy 中,直线l :(21)10k x ky -++=,则当实数k 变化时,原点O 到直线l 的距离的最大值为_____________.【答案】5【详解】由直线(21)10k x ky -++=可化为(1)(2)0x k x y -++=,联立方程组1020x x y -=⎧⎨+=⎩,解得x 1,y 2==-,即直线过定点(1,2)P -,由于直线(21)10k x ky -++=经过定点(1,2)P -,又221(2)5OP =+-=所以原点到直线l 的距离的最大值为5.4.已知点(,)M a b 在直线3410x y +=上,则22a b +的最小值为______【答案】2【详解】由点(,)M a b 在直线上得3410x y +=上,且22a b +表示点M 与原点的距离∴22a b +的最小值为原点到直线3410x y +=的距离,即2210234d ==+∴22a b +的最小值为2故答案为25.两条平行线4310x y +-=与8630x y ++=之间的距离是___________.【答案】12【详解】直线4310x y +-=可化为8620x y +-=,又直线8620x y +-=与直线8630x y ++=的距离为22|3(2)|8+6--,所以平行线4310x y +-=与8630x y ++=之间的距离是12,故答案为:12.6.已知直线1l :10ax y ++=,2l :10x ay ++=.若12l l ∥,则=a ___________,此时1l 与2l 之间的距离为___________.【答案】1-2【详解】直线1l :10ax y ++=,2l :10x ay ++=.若12l l ∥,所以10a a ⋅-=,解得1a =±,当1a =时,1l :10x y ++=,2l :10x y ++=,此时1l 与2l 重合,故舍去;当1a =-时,1l :10x y -++=,2l :10x y -+=,此时1l 与2l 平行;故1a =-;若12l l ∥,即1l :10x y -++=,即1l :10x y --=,2l :10x y -+=,所以1l 与2l 之间的距离为()()2211211--=+-.故答案为:1-,2.7.若直线1:21l y x =-与直线2l 平行,且它们之间的距离等于5,则直线2l 的方程为___________.【答案】240x y -+=或260x y --=【详解】设直线2:2l y x b =+,将直线1l 与直线2l 化为一般式可得1:210l x y --=,2:20l x y b -+=,故它们之间的距离为22152(1)b +=+-,解得4b =或6-,故直线2l 的方程为240x y -+=或260x y --=.故答案为:240x y -+=或260x y --=.8.已知直线l 1,l 2是分别经过A (1,1),B (0,-1)两点的两条平行直线,当l 1,l 2间的距离最大时,直线l 1的方程是________.【答案】x +2y -3=0【详解】当两条平行直线与A ,B 两点的连线垂直时,两条平行直线间的距离最大.因为A (1,1),B (0,-1).所以k AB =-1-10-1=2,所以两条平行直线的斜率为-12,所以直线l 1的方程为y -1=-12(x -1),即x +2y -3=0.高分突破1.与点()21M ,之间的距离为2,且在x 轴上的截距为4的直线是()A .4x =B .34120x y --=C .4x =或34120x y --=D .4y =或34120x y --=【答案】C【详解】4x =与()21M ,的距离为2,在x 轴上的截距为4,故4x =符合要求;对于直线34120x y --=,有22|324112|23(4)d ⨯-⨯-==+-且0y =时4x =,故也符合要求;4y =与()21M ,的距离为3且x 轴无交点,不符合要求.∴4x =、34120x y --=都是与点()21M ,距离为2且在x 轴上的截距为4的直线.故选:C2.直线1l :230x y --=与2l :3610x y -+-=之间的距离为()A .455B .253C .4515D .5【答案】B【详解】由3610x y -+-=可得1203x y -+=,即1l 与2l 平行,故1l 与2l 之间的距离为2231331(252)--=+-.故选:B.3.已知直线330x y +-=和610x my ++=互相平行,则它们之间的距离是()A .4B .1020C .104D .71020【答案】D【详解】由直线平行可得360m -=,解得2m =,则直线方程为6210x y ++=,即1302x y ++=,则距离是221371022031+=+.故选:D.4.冰糖葫芦是中国传统小吃,起源于南宋.由山楂串成的冰糖葫芦如图1所示,若将山楂看成是大小相同的圆,竹签看成一条线段,如图2所示,且山楂的半径(图2中圆的半径)为2,竹签所在的直线方程为20x y +=,则与该串冰糖葫芦的山楂都相切的直线方程为()A .220x y +±=B .250x y +±=C .240x y +±=D .2250x y +±=【答案】D【详解】由题可设与该串冰糖葫芦的山楂都相切的直线方程为20x y c ++=,则22221c =+,∴25c =±,∴与该串冰糖葫芦的山楂都相切的直线方程为2250x y +±=.故选:D.5.①点()3,2P -到直线:34210l x y +-=的距离是___________.②两平行直线3210x y --=和6430x y --=间的距离是___________.【答案】41326【详解】①()3,2,:34210P l x y -+-=;则点P 到直线l 的距离()22334221204534d ⨯+⨯--===+.②6430x y --=即为33202x y --=,所以两平行直线3210x y --=和6430x y --=间的距离22311322632d -==+.6.点P 为直线3420x y +=-上任意一个动点,则P 到点(3,1)-的距离的最小值为___________.【答案】3【详解】由题意得当点P 和点(3,1)-的连线和直线3420x y +=-垂直时距离最小,此时距离等于点(3,1)-到直线3420x y +=-的距离()223341233(4)⨯-⨯-+=+-,故P 到点(3,1)-的距离的最小值为3.故答案为:3.7.点(2,3)P 到直线(1)30mx m y +-+=的距离等于4,则实数m ___________.【答案】47或4【详解】由题意可得:22|23(1)3|4(1)m m m m +-+=⇒+-2103267m m -+=,解得47=m 或4.故答案为:47或4.8.两平行线1:340l x y m ++=与2:680l x y n ++=之间的距离为______.【答案】210m n -【详解】因为直线1:340l x y m ++=,即为1:6820l x y m ++=,所以两平行直线1:340l x y m ++=与2:680l x y n ++=之间的距离为22221068m n m n d --==+.故答案为:210m n-.9.设3450x y +-=,则22x y +的最小值是___________.【答案】1【详解】22xy +表示直线3450x y +-=上任意点(,)P x y 到原点的距离的平方,显然原点到直线3450x y +-=上的点的最小距离就是原点到直线3450x y +-=的距离,即2203045134d ⨯+⨯-==+,所以22x y +的最小值是2211d ==.故答案为:110.已知ABC 的三个顶点的坐标为()3,3A 、()2,2B -、()7,1C -,试求:(1)BC 边上的高所在的直线方程;(2)ABC 的面积.【答案】(1)360x y --=;(2)24【详解】(1)因为2112(7)3BC k --==---,则BC 边上的高的斜率为3,又经过A 点,故方程为()333y x -=-,化简得360x y --=.(2)()2227(21)310BC =++--=,直线BC 方程为12(2)3y x +=--,整理得340x y ++=,则A 到BC 的距离为223334161013+⨯+=+,则ABC 的面积为11631024210⨯⨯=.11.求与直线3240x y -+=平行且距离等于3的直线.【答案】3243130x y -++=或3243130x y -+-=.【详解】设所求直线方程为320x y m -+=,由()22|4|332m -=+-,得4313m =+或4313m =-,所以与直线3240x y -+=平行且距离等于3的直线方程为3243130x y -++=或3243130x y -+-=.12.两平行直线1l ,2l 分别过()1,0A ,()0,5B .(1)1l ,2l 之间的距离为5,求两直线方程;(2)若1l ,2l 之间的距离为d ,求d 的取值范围.【答案】(1)12:0,:5l y l y ==或12:51250,:512600l x y l x y --=-+=;(2)(0,26⎤⎦【详解】(1)当1l ,2l 斜率不存在时,易知12:1,:0l x l x ==,1l ,2l 之间的距离为1,不合题意;当1l ,2l 斜率存在时,设斜率为k ,则12:(1),:5l y k x l y kx =--=,化为一般式得1:0l kx y k --=,2:50l kx y -+=,由1l ,2l 之间的距离为5,可得()22551k k --=+-,解得0k =或512k =,当0k =时,12:0,:5l y l y ==;当512k =时,12:51250,:512600l x y l x y --=-+=.故两直线方程为12:0,:5l y l y ==或12:51250,:512600l x y l x y --=-+=.(2)如图:当1l ,2l 旋转到和AB 垂直时,1l ,2l 之间的距离d 最大为()2210(05)26-+-=,当1l ,2l 旋转到和AB 重合时,距离为0,又两平行直线1l ,2l 不重合,故(0,26d ⎤∈⎦.13.已知直线1:320l x y ++=与2:20l mx y n ++=平行,且直线1l 与直线2l 之间的距离为10,求m 、n 的值.【详解】因为直线1:320l x y ++=与2:20l mx y n ++=平行,所以2312m n =≠,解得6m =,4n ¹,又因为直线1l 与直线2l 之间的距离为10,所以2241062n -=+,解得24n =或16n =-.综上,m 的值为6;n 的值为24或16-.14.已知(4,3)A -、(2,1)B -和直线:4320l x y +-=,若坐标平面内存在一点P ,使PA PB =,且点P 到直线l 的距离为2,求点P 的坐标.【详解】设点P 的坐标为(,)a b .∵(4,3)A -,(2,1)B -,所以线段AB 的中点M 的坐标为(3,2)-.而AB 所在直线的斜率31142AB k -+==--,∴线段AB 的垂直平分线方程为23y x +=-,即50x y --=.∵点(,)P a b 在直线50x y --=上,∴50a b --=……①;又点(,)P a b 到直线4320x y +-=的距离为2,∴22432243a b +-=+,即43210a b +-=±……②.联立①②,解得1,4,a b =⎧⎨=-⎩或27,78.7a b ⎧=⎪⎪⎨⎪=-⎪⎩故所求点P 的坐标为(1,4)-或278,77⎛⎫- ⎪⎝⎭.故答案为(1,4)-或278,77⎛⎫- ⎪⎝⎭15.已知平行四边形ABCD ,(1,2)A 、(2,4)B 、1(,5)2C ,求:(1)点D 的坐标及点A 到直线CD 的距离;(2)平行四边形ABCD 的面积.【详解】(1)设点00(,)D x y ,则有线段BD 的中点坐标为00(1,2)22x y ++,依题意,线段AC 中点坐标为37(,)42,由平行四边形性质知:0031247222x y ⎧+=⎪⎪⎨⎪+=⎪⎩,解得001,32x y =-=,所以点D 的坐标为1(,3)2D -;直线CD 的斜率53211()22k -==--,直线CD 的方程为152()2y x -=-,即240x y -+=,所以点(1,2)A 到直线CD 的距离22|2124|4552(1)d ⨯-+==+-.(2)由(1)知,线段CD 长2211||()(35)522CD =--+-=,所以平行四边形ABCD 的面积45||545S CD d =⋅=⨯=.。
