第4讲 等参元和高斯积分
合集下载
FE-Ch04.1-5等参元与数值积分
形函数Ni (ξ,η)在单元的i结点上的值为1， 在其它结点上的值均为0。
坐标变换式采用如下相似的公式，
x = ∑ N i (ξ ,η ) xi
i =1 8 8
（4-12）
y = ∑ N i (ξ ,η ) y i
i =1
将ξ=1代入公式（4-12），可以得到单元345边在 ξ=1 4-12 345 整体坐标下的参数方程：
N3 =
1 (1 − ξ )(1 + η ) 4
（4-5）
1 N 4 = (1 + ξ )(1 + η ) 4
四个结点的坐标为
(ξ i ,ηi )
，定义新的变量，
(i=1，2，3，4)
ξ 0 = ξ iξ ， η 0 = ηiη
(4-6)
形态函数表示为，N i
1 = (1 + ξ 0 )(1 + η 0 ) (i=1，2，3，4) 4
如果单元不是等参的, 即坐标插值:
x = ∑ N i (ξ ,η ) xi
i =1 m
y = ∑ N i (ξ ,η ) yi
i =1
m
中的节点数m和插值函数Ni, 各自不等于未知函数 n ’: φ插值中的节点数n和插值函数Nk ϕ = N ' (ξ ,η )ϕ
∑
k =1
k
k
这时,可以分两种情况: (1)超参单元, 即坐标插值节点数m>未知函数φ插值节 点数n, 单元一般不满足完备性的要求 (2)次参单元, 即m<n, 从构造变节点单元的一般方法, 假定一2D等参单元在各节点有线性变化的场函数, Φ=a+bx+cy 其在各节点有对应的场函数值, Φi=a+bxi+cyi (i=1,2,…,n)
《有限元基础及应用》课程大纲
《有限元基础及应用》课程教学大纲一、课程基本信息二、课程目标（一）总体目标：有限元法是求解复杂工程问题进行数值模拟非常有效的方法，是现代数字化科技的一种重要基础性原理。
将它应用于科学研究中，可以成为探究物质客观规律的先进手段；将它应用于工程技术中，可成为工程设计和分析的可靠工具。
有限元法已经成为机械工程、车辆工程、航空航天工程、土木建筑等专业的必修课或选修课，有限元商用软件也是广大工程技术人员从事产品开发、设计、分析，以及生产服务的重要工具。
通过本课程的学习使同学们掌握有限元分析方法的基础知识和原理；掌握大型有限元分析软件（ANSYS）的使用；有限元方法的实际应用：能够针对具有复杂几何形状的变形体完整获取复杂外力作用下它内部准确力学信息，在准确进行力学分析的基础上，可以对所研究对象进行强度、刚度等方面的判断，以便对研究结构进行静态、动态的强度和刚度分析、参数设计以及结构优化设计。
内容由浅入深，通俗易懂，结合实践应用分析，培养学生理论联系实际和解决实际问题的能力。
（二）课程目标：课程目标1：掌握有限元方法的基本原理，分析过程和步骤，形函数的构造方法，以及针对不同维度、不同结构准确选择合适的单元的技巧；课程目标2：掌握有限元分析方法，具有对不同工程问题建立相应力学模型再选取适合的有限元模型离散，最后得到高精度低成本的数值模拟结果；课程目标3：利用有限元原理和应用软件（ANSYS），能够针对车辆结构中具有复杂几何形状的零部件完整获取复杂外力作用下其内部的准确力学信息（位移、应力和应变），并能根据强度、刚度、稳定性及疲劳等进行分析判断结构的安全性，具有分析和解决工程实际问题的能力；课程目标4：掌握大型商用有限元软件（ANSYS）对车辆结构部件的静力学、动力学和多物理场耦合问题进行数值模拟和分析。
能够了解不同单元的适用范围以及有限元方法数值模拟的局限性。
（三）课程目标与毕业要求、课程内容的对应关系本课程支撑专业培养计划中毕业要求1、2、3、5。
4.3 高斯积分
节点xk 及求积系数 Ak 的选取方法
由特殊函数理论知，勒让德（Legendre）多项式
1 dn p n ( x) = n ⋅ n [( x 2 − 1) n ] 2 n! dx
在[-1，1]上是正交的，即 1 ∫Байду номын сангаас1 pn ( x) pn+1 ( x)dx = 0
[2(n + 1)]! p n+1 ( x )的首项系数为： n+1 ，故常取 2 [(n + 1)!]2
三点(n=2)高斯法计算子程序 subroutine Gauss(a,b,G) dimension t(3),w(3) data t/0.,0.774597,-0.774597/ data w/0.888889,0.555556,0.555556/ G=0.0 1 1 x = (b + a) + (b − a)t do 10 i=1,3 2 2 x=0.5*[(b+a)+(b-a)*t(i)] n 1 10 G=G+w(i)*f(x) ∫−1 f ( x)dx ≈ ∑ Ak f ( xk ) k =0 G=0.5*(b-a)*G return b−a f ( x)dx = ∫ ∫ ϕ (t )dt end 2
以上讨论中，积分区间为[-1,1]。 当实际计算区间为 [a, b] ,可采用如下变量替换：
1 1 x = (b + a) + (b − a)t 2 2
则积分区间 [a, b] 变为[-1,1]，且积分变为：
∫
b
a
b−a 1 f ( x)dx = ∫−1ϕ (t )dt 2
a+b b−a + t) 其中 ϕ (t ) = f ( 2 2
数值分析-高斯求积分
p( x)ωn ( x)dx
Ak p( xk )ωn ( xk ) 0
a
k1
即ωn( x)与任意次数不超过n 1的多项式p( x)
在[a, b]上正交
充分性：如果w(x)与任意次数不超过n-1的多项式正 交，则其零点必为Gauss点
设f ( x)为任意次数不超过2n 1次的多项式,
用n ( x)除f ( x)得
3.6 高斯（Gauss）型求积公式
主要内容
• 具有(n+1)个求积节点的Newton-Cotes公式，
b
n
f ( x)dx
Ak f ( xk )
a
k1
至少具有n阶代数精度
•在确定求积公式求积系数Ak的过程中限定求积节点 为等分节点，简化了处理过程，但也降低了求积公 式的代数精度
去掉求积节点 为等分节点的限制条件，会有什么 结果？？
1v( x)du(n 1)( x)
-1
1
1
u(n 1)( x)v ( x)d x
-1
v(1)u(n 1) (1) v(1)u(n 1) (1)
1
u(n 1) ( x)v ( x)d x
-1
v (1)u(n 2) (1)
1
u(n 2) ( x)v ( x)d x
-1
v(1)u(n 1) (1) v (1)u(n 2) (1)
a
证明： 必要性： 若x1, x2 ,, xn是高斯点,则求积公式
b
f ( x)dx
a
n
Ak f ( xk )具有2n 1次代数精度
k1
作多项式, ωn( x) ( x x1)( x x2 ) ( x xn ), 设p( x)为
高斯积分的计算方法
高斯积分的计算方法在数学领域内，高斯积分是一类经典的数学积分，它不仅深受广大数学学者的喜爱，更在科学与工程领域内应用广泛。
高斯积分的计算方法在数学的发展史上也有着突出的地位。
高斯积分的概念及应用高斯积分是计算圆柱体体积的重要方法之一，它起源于高斯儿时曾在数学竞赛时受到圆柱体体积的启发，从而产生了求出圆柱体体积的积分方法，这就是高斯积分。
高斯积分包含两种类型，第一类和第二类。
第一类和第二类高斯积分分别用于计算复平面中的任意四边形及半平面上的积分问题，是极其有用的数学工具。
在物理学中，高斯积分也运用得非常广泛，可以用来求解电场、磁场、热力学等问题。
高斯积分的计算一般多使用复数表示，复数的实部和虚部对应于二维空间中的横坐标和纵坐标。
对于复平面上的第一类高斯积分，可以利用复变量的奇偶性质以及圆形映射将圆上的高斯积分转化为实轴上的积分问题，从进而求解高斯积分。
对于第二类高斯积分，通常采用变形的方式将积分式转化为反常积分，然后再利用数值解法或者级数展开法求解反常积分。
具体而言，我们将复平面的积分路径展开为两条道路，设积分函数为f(z)，则当选取的路径使得沿路径的积分无穷大时，在道路由初始点z1到终止点z2的方向上分别分割成R和r两段，则有以下套路的计算方式：∫(z1,z2)f(z)dz = ∫R f(z)dz + ∫r f(z)dz其中∫R f(z)dz表示对有限的路径积分进行求解，而∫r f(z)dz则表示计算路径积分的一部分，因此在变形之后我们只需要将∫r f(z)dz 根据变形后的路径进行求解即可。
总结高斯积分作为经典数学积分，在物理、工程以及金融领域都有着广泛的应用。
高斯积分的计算也有着不同的方法，需要根据实际问题的需求不断灵活运用。
不过，绝大多数情况下我们都可以采用圆形映射的方法统一化计算，以及采用变形的方式将积分式转化为反常积分进行求解。
《高斯公式》课件
其中，$S$是一个曲面，$\ partial S$是该曲面的边界，$\ mathbf{F}$是一个 三维矢量场，$\ mathbf{n}$是曲面在某一点的法向量，$dV$代表三维空间 中的体积元素，$dS$代表曲面上的面积元素。
高斯公式的应用
高斯公式被广泛用于电场和磁场的计算中。通过使用高斯公式，可以将一个 定义在三维空间中的矢量场转换为曲面积分的形式，并由此进行求解。例如， 使用高斯公式可以计算出一个点电荷产生的电场，或者一个长导线周围的磁 场强度。
总结
高斯公式是一个重要的数学定理，用于计算曲面与其边界之间的积分。它在电场和磁场计算中有广泛的应用， 能够帮助我们了解和分析这些矢量场
通过高斯公式，我们可以计算出 电场力线的分布情况，进而得到 电场的性质和分布规律。
电场计算公式
使用高斯公式，可以通过已知电 场力线的边界情况，求解出电场 的数学表达式，从而进行进一步 的计算。
等势面的绘制
通过高斯公式计算得到的电场数 据，可以用于绘制等势面图，帮 助我们更直观地理解电场的分布 特征。
磁场计算示例
1
定向导线的磁场计算
使用高斯公式，我们可以计算出特定形
磁场强度的求解
2
状的导线产生的磁场分布，并且了解其 大小和方向。
通过应用高斯公式，可以求解磁场强度
在不同点的数值，从而更清楚地了解磁
场的特性和分布。
3
磁场环路的计算
利用高斯公式，可以计算出磁场环路的 磁感应强度，帮助我们理解磁场的传输 和衰减过程。
《高斯公式》PPT课件
在本次课件中，我们将探讨高斯公式的概念、公式表达式以及它在电场和磁 场计算中的应用。
什么是高斯公式？
高斯公式是一个三元组的数学定理，用于计算一个维度为2的曲面与其边界之间的积分。
高斯公式的应用
高斯公式被广泛用于电场和磁场的计算中。通过使用高斯公式，可以将一个 定义在三维空间中的矢量场转换为曲面积分的形式，并由此进行求解。例如， 使用高斯公式可以计算出一个点电荷产生的电场，或者一个长导线周围的磁 场强度。
总结
高斯公式是一个重要的数学定理，用于计算曲面与其边界之间的积分。它在电场和磁场计算中有广泛的应用， 能够帮助我们了解和分析这些矢量场
通过高斯公式，我们可以计算出 电场力线的分布情况，进而得到 电场的性质和分布规律。
电场计算公式
使用高斯公式，可以通过已知电 场力线的边界情况，求解出电场 的数学表达式，从而进行进一步 的计算。
等势面的绘制
通过高斯公式计算得到的电场数 据，可以用于绘制等势面图，帮 助我们更直观地理解电场的分布 特征。
磁场计算示例
1
定向导线的磁场计算
使用高斯公式，我们可以计算出特定形
磁场强度的求解
2
状的导线产生的磁场分布，并且了解其 大小和方向。
通过应用高斯公式，可以求解磁场强度
在不同点的数值，从而更清楚地了解磁
场的特性和分布。
3
磁场环路的计算
利用高斯公式，可以计算出磁场环路的 磁感应强度，帮助我们理解磁场的传输 和衰减过程。
《高斯公式》PPT课件
在本次课件中，我们将探讨高斯公式的概念、公式表达式以及它在电场和磁 场计算中的应用。
什么是高斯公式？
高斯公式是一个三元组的数学定理，用于计算一个维度为2的曲面与其边界之间的积分。
有限元分析4二维单元
二维单元
矩形单元 平面四边形单元 线性三角形单元 平面三角形单元 等参单元 二维积分：高斯－勒让德多项式
一、矩形单元 一维的解是由线段近似的，而二维的解是由 平面片近似的。 仍以温度函数为例，研究二维空间问题，假 设温度在X和Y方向均会发生变化。温度沿单元的 分布是X坐标和Y坐标的函数：
三角形自然（面积）坐标与形函数 si , s j , sk 是完全相同的， 即：
si sj sk
例如：
1 X jYk X kYj X (Y j Yk ) Y ( X k X j ) A1 2 si 1 A X i Y j Yk X j Yk Yi X k Yi Y j 2
将以下条件应用到方程中得到b1，b2，b3，b4：
b1 Ti
1 b3 (Tn Ti ) w
与一维单元相同，可以得到对于典型单元由 形函数表示的温度分布：
T ( e ) si s j sm
Ti T j sn T m Tn
4.平面三角形单元
如果区域内有某个变量（如温度）随空间发生变化， 可以用二次函数来更精确的近似，例如：
T (e) a1 a2 X a3Y a4 X a5 XY a6Y
2
2
由自然坐标表示的形函数为：
si (2 1) s j (2 1) sk (2 1) 1 3( ) 2( ) sl 4 sm 4 4 (1 ) sn 4 4 (1 )
3.线性三角形单元
三角形单元由三个节点定义，可以用下式表示三角形区 域内独立变量的变化：
矩形单元 平面四边形单元 线性三角形单元 平面三角形单元 等参单元 二维积分：高斯－勒让德多项式
一、矩形单元 一维的解是由线段近似的，而二维的解是由 平面片近似的。 仍以温度函数为例，研究二维空间问题，假 设温度在X和Y方向均会发生变化。温度沿单元的 分布是X坐标和Y坐标的函数：
三角形自然（面积）坐标与形函数 si , s j , sk 是完全相同的， 即：
si sj sk
例如：
1 X jYk X kYj X (Y j Yk ) Y ( X k X j ) A1 2 si 1 A X i Y j Yk X j Yk Yi X k Yi Y j 2
将以下条件应用到方程中得到b1，b2，b3，b4：
b1 Ti
1 b3 (Tn Ti ) w
与一维单元相同，可以得到对于典型单元由 形函数表示的温度分布：
T ( e ) si s j sm
Ti T j sn T m Tn
4.平面三角形单元
如果区域内有某个变量（如温度）随空间发生变化， 可以用二次函数来更精确的近似，例如：
T (e) a1 a2 X a3Y a4 X a5 XY a6Y
2
2
由自然坐标表示的形函数为：
si (2 1) s j (2 1) sk (2 1) 1 3( ) 2( ) sl 4 sm 4 4 (1 ) sn 4 4 (1 )
3.线性三角形单元
三角形单元由三个节点定义，可以用下式表示三角形区 域内独立变量的变化：
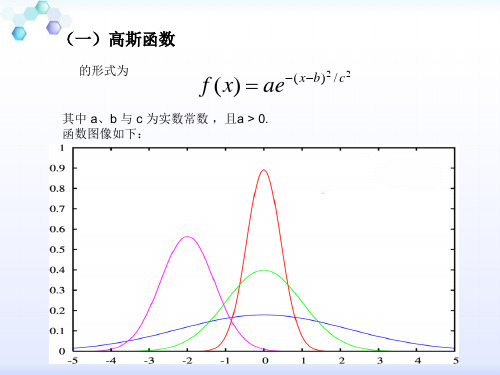
高斯函数.ppt
1 2n n 0,1,2....
其实上述要求就是对谐振子能量有一定的限制，即
E En (n 1/ 2) n 0,1,2...
利用正交性公式：
Hm ( )Hn ( )e 2 d 2n n！mn
可以证明，一维谐振子能量本征函数（实）为：
n (x) Ane2x2 /2Hn (x)
An / 2n n！1/2
f
(
z)
1 2(
z)
(1
2iz
k0 2
)
（12）
因此，（2）中的高斯函数为：
e f (z)(x2 y2 )
exp[
x2 y2
2 (z)
(1
2iz
k02
)]
（13）
函数g（z）的表达式（9）可写为：
g(z)
u0
(
2z
k0
2
)
2
ei
u0
0
ei
（14）
2z
arctan( k02
)
（15）
将（13）（14）代入（2）（4）式得光束场强函数：
u(x,
y,
z)
u0
0
e e
x
2y 2
2
i
k
z
k(x2 y2
2z[1 (02k
) )2
]
2z
（16） （17）
式中因子ei 是相因子，其余的因子表示各点的波幅。
因子
e
x
2y 2
2
是限制波束宽度的因子。波束宽度由函数w（z）代表。 由（12）式，在z=0点，波束具有最小宽度，该处称为光 束腰部。离腰部越远处波束的宽度越大。
1.方垒型波列
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 N1 = 4 (1 − ξ )(1 − η ) N = 1 (1 + ξ )(1 − η ) 2 4 1 N 3 = 4 (1 + ξ )(1 + η ) N = 1 (1 − ξ )(1 + η ) 4 4
北京航空航天大学
x N1 = y 0
0 N1
N2 0
0 N2
N3 0
0 N3
N4 0
u( x(ξ ,η ), y (ξ ,η )) = N(ξ ,η )q e
北京航空航天大学
u1 v 1 u2 0 v2 N 4 u3 v3 u4 v 4
1 N1 = (1 − ξ )(1 − η ) 4 N = 1 (1 + ξ )(1 − η ) 2 4
∂Ni ∂x = ∂N i = ∂y
?
1 N 3 = (1 + ξ )(1 + η ) 4 N = 1 (1 − ξ )(1 + η ) 4 4
单元的几何坐标与位移用同样的节点和相同的形 状函数通过插值的方式表示。形状函数用自然坐 标给出。
x(ξ ,η ) = N(ξ ,η )x e
u( x(ξ ,η ), y (ξ ,η )) = u(ξ ,η ) = N(ξ ,η )q e
1 N1 = (1 − ξ )(1 − η ) 4 N = 1 (1 + ξ )(1 − η ) 2 4 1 N 3 = (1 + ξ )(1 + η ) 4 N = 1 (1 − ξ )(1 + η ) 4 4
T
P = ∫ N ptCdη
−1
在ξ = 常数的面上
1/ 2
∂x 2 ∂y 2 C = + ∂η ∂η
北京航空航天大学
四边形等参单元形状要求
避免出现
J =0
不能有重节点 不能出现内角大于180o的情况 内角最好介于30o-150o之间（有限变形的情况）
u1 = α1 − α 2 − α 3 + α 4 u = α + α − α − α 2 1 2 3 4 u3 = α1 + α 2 + α 3 + α 4 u4 = α1 − α 2 + α 3 − α 4
α1 1 1 1 1 u1 α 2 1 −1 1 1 − 1 u2 = α 3 4 −1 − 1 1 1 u3 α 4 1 − 1 1 − 1 u4
节点条件： ui = u (ξi ,ηi ) vi = v (ξi ,ηi )
(ξ1 ,η1 ) = (−1, −1) (ξ 2 ,η 2 ) = (1, −1)
(ξ3 ,η3 ) = (1,1) (ξ 4 ,η4 ) = (−1,1)
北京航空航天大学
u1 = α1 + α 2ξ1 + α 3η1 + α 4ξ1η1 u = α + α ξ + α η + α ξ η 2 1 2 2 3 2 4 2 2 u3 = α1 + α 2ξ3 + α 3η3 + α 4ξ3η3 u4 = α1 + α 2ξ 4 + α 3η4 + α 4ξ 4η4
第4讲 等参单元和数值积分
金朝海 jch666@
北京航空航天大学
实际问题常常需要使用一些几何形状不太规整 的单元来逼近原问题。直接研究这些不规整单 元的表达式比较困难（在整体坐标系下构造位 移插值函数，则计算形状函数矩阵、单元刚度 矩阵及等效节点载荷列阵时十分冗繁）。事实 上，形状不规整的单元和形状规整的单元（矩 形单元、正六面体单元）可以建立一种映射关 系，使得物理坐标系中的整体坐标和自然坐标 系中的局部坐标一一对应。 等参单元的提出为有限元法成为现代工程实际 等参单元 领域最有效的数值分析方法迈出了极为重要的 一步。
节点条件： xi = x(ξi ,ηi ) yi = y (ξi ,ηi )
x1 = α1 + α 2ξ1 + α 3η1 + α 4ξ1η1 x = α + α ξ + α η + α ξ η 2 1 2 2 3 2 4 2 2 x3 = α1 + α 2ξ3 + α 3η3 + α 4ξ3η3 x4 = α1 + α 2ξ 4 + α 3η4 + α 4ξ 4η4
北京航空航天大学
ε( x(ξ ,η ), y (ξ ,η )) = [ ∂ ] u(ξ ,η ) = [ ∂ ] N(ξ ,η )q e = B(ξ ,η )q e
∂ 0 ∂x ∂ N1 0 N 2 0 N 3 0 N 4 0 B(ξ ,η ) = 0 ∂y 0 N1 0 N 2 0 N 3 0 N 4 ∂ ∂ ∂y ∂x
u ( x(ξ ,η ), y (ξ ,η )) = α1 + α 2ξ + α 3η + α 4ξη = N1u1 + N 2u2 + N 3u3 + N 4u4 v( x(ξ ,η ), y (ξ ,η )) = β1 + β 2ξ + β 3η + β 4ξη = N1v1 + N 2 v2 + N 3v3 + N 4 v4
∂N i ∂N i ∂x −1 ∂ξ ∂N = J ∂N i i ∂y ∂η
北京航空航天大学
K = ∫ e B ( x(ξ ,η ), y (ξ ,η ))DB( x(ξ ,η ), y (ξ ,η ))tdxdy
北京航空航天大学
4.1 等参单元
等参单元定义的给出 平面问题四边形等参单元计算公式 三维问题六面体等参单元计算公式 采用等参单元的优点
北京航空航天大学
等参单元定义的给出
等参单元：用同样的节点和相同的形状函 数通过插值的方式表示出单元的几何坐标 与位移的单元，称为等参单元。 等参单元的插值函数用自然坐标给出。 如果坐标变换节点数多于位移插值的节点 数，称为超参变换。反之，如果坐标变换 节点数少于位移插值的节点数，则称为亚 参变换。
北京航空航天大学
平面问题四边形等参单元的推导
坐标映射
( x x1 , y1 )
P (ξ ,η )
( x2 , y2 )
整体直角坐标
（一般四边形）
P ( x, y )
单元局部自然坐标
（规格化的矩形）
映射
P (ξ ,η )
北京航空航天大学
P ( x, y )
北京航空航天大学
∂N i ∂Ni ∂x ∂Ni ∂ξ = ∂x ∂ξ + ∂y ∂N i = ∂Ni ∂x + ∂N i ∂η ∂x ∂η ∂y ∂N i ∂x ∂ξ ∂ξ = ∂N i ∂x ∂η ∂η
0 N1
N2 0
0 N2
N3 0
0 N3
N4 0
x1 y 1 x2 0 y2 N 4 x3 y3 x4 y 4
x(ξ ,η ) = N(ξ ,η )x e
北京航空航天大学
位移函数
( x3 , y3 )
e
T
S
=∫
e
1
−1 −1
∫
1
B (ξ ,η )DB(ξ ,η )t J d ξ dη = ∫
T
T T
1
−1 −1
∫
1
F(ξ ,η ) J d ξ dη
e P = ∫ e N bdV + ∫ e N pdA = Pbe + Pp Ω 1 Sp
P =∫
e b e p
−1 −1 1
T
∫
1
N b J td ξ dη
同理可得：
β1 1 1 1 1 v1 β 2 1 −1 1 1 − 1 v2 = β3 4 −1 − 1 1 1 v3 β4 1 − 1 1 − 1 v4
北京航空航天大学
( x4 , y4 )
(−1,1)
(1,1)
( x2 , y2 ) ( x1 , y1 )
(−1, −1)
(1, −1)
u ( x(ξ ,η ), y (ξ ,η )) = u (ξ ,η ) = α1 + α 2ξ + α 3η + α 4ξη v( x(ξ ,η ), y (ξ ,η )) = v(ξ ,η ) = β1 + β 2ξ + β3η + β 4ξη
映射
P (ξ ,η )
x = x(ξ ,η ) y = y (ξ ,η )
构造插值函数 x = α1 + α 2ξ + α 3η + α 4ξη y = β1 + β 2ξ + β 3η + β 4ξη
(ξ1 ,η1 ) = (−1, −1) (ξ 2 ,η 2 ) = (1, −1) (ξ3 ,η3 ) = (1,1) (ξ 4 ,η4 ) = (−1,1)
∂y ∂ξ ∂y ∂η
偏导数变换
∂y ∂N i ∂Ni ∂ξ ∂x ∂x = J ∂N ∂y ∂N i i ∂y ∂η ∂y J* J = J
−1
雅可比矩阵：
∂x ∂ξ J= ∂x ∂η ∂y ∂ξ ∂y ∂η
北京航空航天大学
x N1 = y 0
0 N1
N2 0
0 N2
N3 0
0 N3
N4 0
u( x(ξ ,η ), y (ξ ,η )) = N(ξ ,η )q e
北京航空航天大学
u1 v 1 u2 0 v2 N 4 u3 v3 u4 v 4
1 N1 = (1 − ξ )(1 − η ) 4 N = 1 (1 + ξ )(1 − η ) 2 4
∂Ni ∂x = ∂N i = ∂y
?
1 N 3 = (1 + ξ )(1 + η ) 4 N = 1 (1 − ξ )(1 + η ) 4 4
单元的几何坐标与位移用同样的节点和相同的形 状函数通过插值的方式表示。形状函数用自然坐 标给出。
x(ξ ,η ) = N(ξ ,η )x e
u( x(ξ ,η ), y (ξ ,η )) = u(ξ ,η ) = N(ξ ,η )q e
1 N1 = (1 − ξ )(1 − η ) 4 N = 1 (1 + ξ )(1 − η ) 2 4 1 N 3 = (1 + ξ )(1 + η ) 4 N = 1 (1 − ξ )(1 + η ) 4 4
T
P = ∫ N ptCdη
−1
在ξ = 常数的面上
1/ 2
∂x 2 ∂y 2 C = + ∂η ∂η
北京航空航天大学
四边形等参单元形状要求
避免出现
J =0
不能有重节点 不能出现内角大于180o的情况 内角最好介于30o-150o之间（有限变形的情况）
u1 = α1 − α 2 − α 3 + α 4 u = α + α − α − α 2 1 2 3 4 u3 = α1 + α 2 + α 3 + α 4 u4 = α1 − α 2 + α 3 − α 4
α1 1 1 1 1 u1 α 2 1 −1 1 1 − 1 u2 = α 3 4 −1 − 1 1 1 u3 α 4 1 − 1 1 − 1 u4
节点条件： ui = u (ξi ,ηi ) vi = v (ξi ,ηi )
(ξ1 ,η1 ) = (−1, −1) (ξ 2 ,η 2 ) = (1, −1)
(ξ3 ,η3 ) = (1,1) (ξ 4 ,η4 ) = (−1,1)
北京航空航天大学
u1 = α1 + α 2ξ1 + α 3η1 + α 4ξ1η1 u = α + α ξ + α η + α ξ η 2 1 2 2 3 2 4 2 2 u3 = α1 + α 2ξ3 + α 3η3 + α 4ξ3η3 u4 = α1 + α 2ξ 4 + α 3η4 + α 4ξ 4η4
第4讲 等参单元和数值积分
金朝海 jch666@
北京航空航天大学
实际问题常常需要使用一些几何形状不太规整 的单元来逼近原问题。直接研究这些不规整单 元的表达式比较困难（在整体坐标系下构造位 移插值函数，则计算形状函数矩阵、单元刚度 矩阵及等效节点载荷列阵时十分冗繁）。事实 上，形状不规整的单元和形状规整的单元（矩 形单元、正六面体单元）可以建立一种映射关 系，使得物理坐标系中的整体坐标和自然坐标 系中的局部坐标一一对应。 等参单元的提出为有限元法成为现代工程实际 等参单元 领域最有效的数值分析方法迈出了极为重要的 一步。
节点条件： xi = x(ξi ,ηi ) yi = y (ξi ,ηi )
x1 = α1 + α 2ξ1 + α 3η1 + α 4ξ1η1 x = α + α ξ + α η + α ξ η 2 1 2 2 3 2 4 2 2 x3 = α1 + α 2ξ3 + α 3η3 + α 4ξ3η3 x4 = α1 + α 2ξ 4 + α 3η4 + α 4ξ 4η4
北京航空航天大学
ε( x(ξ ,η ), y (ξ ,η )) = [ ∂ ] u(ξ ,η ) = [ ∂ ] N(ξ ,η )q e = B(ξ ,η )q e
∂ 0 ∂x ∂ N1 0 N 2 0 N 3 0 N 4 0 B(ξ ,η ) = 0 ∂y 0 N1 0 N 2 0 N 3 0 N 4 ∂ ∂ ∂y ∂x
u ( x(ξ ,η ), y (ξ ,η )) = α1 + α 2ξ + α 3η + α 4ξη = N1u1 + N 2u2 + N 3u3 + N 4u4 v( x(ξ ,η ), y (ξ ,η )) = β1 + β 2ξ + β 3η + β 4ξη = N1v1 + N 2 v2 + N 3v3 + N 4 v4
∂N i ∂N i ∂x −1 ∂ξ ∂N = J ∂N i i ∂y ∂η
北京航空航天大学
K = ∫ e B ( x(ξ ,η ), y (ξ ,η ))DB( x(ξ ,η ), y (ξ ,η ))tdxdy
北京航空航天大学
4.1 等参单元
等参单元定义的给出 平面问题四边形等参单元计算公式 三维问题六面体等参单元计算公式 采用等参单元的优点
北京航空航天大学
等参单元定义的给出
等参单元：用同样的节点和相同的形状函 数通过插值的方式表示出单元的几何坐标 与位移的单元，称为等参单元。 等参单元的插值函数用自然坐标给出。 如果坐标变换节点数多于位移插值的节点 数，称为超参变换。反之，如果坐标变换 节点数少于位移插值的节点数，则称为亚 参变换。
北京航空航天大学
平面问题四边形等参单元的推导
坐标映射
( x x1 , y1 )
P (ξ ,η )
( x2 , y2 )
整体直角坐标
（一般四边形）
P ( x, y )
单元局部自然坐标
（规格化的矩形）
映射
P (ξ ,η )
北京航空航天大学
P ( x, y )
北京航空航天大学
∂N i ∂Ni ∂x ∂Ni ∂ξ = ∂x ∂ξ + ∂y ∂N i = ∂Ni ∂x + ∂N i ∂η ∂x ∂η ∂y ∂N i ∂x ∂ξ ∂ξ = ∂N i ∂x ∂η ∂η
0 N1
N2 0
0 N2
N3 0
0 N3
N4 0
x1 y 1 x2 0 y2 N 4 x3 y3 x4 y 4
x(ξ ,η ) = N(ξ ,η )x e
北京航空航天大学
位移函数
( x3 , y3 )
e
T
S
=∫
e
1
−1 −1
∫
1
B (ξ ,η )DB(ξ ,η )t J d ξ dη = ∫
T
T T
1
−1 −1
∫
1
F(ξ ,η ) J d ξ dη
e P = ∫ e N bdV + ∫ e N pdA = Pbe + Pp Ω 1 Sp
P =∫
e b e p
−1 −1 1
T
∫
1
N b J td ξ dη
同理可得：
β1 1 1 1 1 v1 β 2 1 −1 1 1 − 1 v2 = β3 4 −1 − 1 1 1 v3 β4 1 − 1 1 − 1 v4
北京航空航天大学
( x4 , y4 )
(−1,1)
(1,1)
( x2 , y2 ) ( x1 , y1 )
(−1, −1)
(1, −1)
u ( x(ξ ,η ), y (ξ ,η )) = u (ξ ,η ) = α1 + α 2ξ + α 3η + α 4ξη v( x(ξ ,η ), y (ξ ,η )) = v(ξ ,η ) = β1 + β 2ξ + β3η + β 4ξη
映射
P (ξ ,η )
x = x(ξ ,η ) y = y (ξ ,η )
构造插值函数 x = α1 + α 2ξ + α 3η + α 4ξη y = β1 + β 2ξ + β 3η + β 4ξη
(ξ1 ,η1 ) = (−1, −1) (ξ 2 ,η 2 ) = (1, −1) (ξ3 ,η3 ) = (1,1) (ξ 4 ,η4 ) = (−1,1)
∂y ∂ξ ∂y ∂η
偏导数变换
∂y ∂N i ∂Ni ∂ξ ∂x ∂x = J ∂N ∂y ∂N i i ∂y ∂η ∂y J* J = J
−1
雅可比矩阵：
∂x ∂ξ J= ∂x ∂η ∂y ∂ξ ∂y ∂η