评分排序优化模型
大众点评评分算法

大众点评评分算法1. 简介大众点评是中国最大的本地生活服务平台,用户可以在平台上搜索、浏览和评论各类商家和服务。
为了提供更好的用户体验,大众点评采用了一套评分算法来对商家进行评级。
本文将详细介绍大众点评的评分算法。
2. 评分计算方法大众点评的评分计算方法主要包括两个方面:综合得分计算和排序策略。
2.1 综合得分计算综合得分是根据用户对商家的评论和打分来计算的,主要考虑以下几个因素:2.1.1 用户打分用户可以给商家打出5星、4星、3星、2星或1星的评价,其中5星为最高,1星为最低。
每个星级对应一个权重值,一般情况下,5星权重最高,而1星权重最低。
2.1.2 用户评论用户可以对商家进行文字评论,并且可以选择是否推荐该商家。
推荐与否也会影响综合得分的计算。
如果用户推荐该商家,则会有额外加分;反之则不会。
2.1.3 用户等级大众点评根据用户的活跃程度和贡献度,给予用户不同的等级。
高等级用户的评论和打分会有更大的权重。
通过以上因素的综合考虑,大众点评可以计算出商家的综合得分。
2.2 排序策略大众点评还采用了一套排序策略来对商家进行排名。
排序策略主要考虑以下几个因素:2.2.1 综合得分商家的综合得分是排序的主要依据,得分越高,排名越靠前。
2.2.2 评论数量商家的评论数量也是影响排序的重要因素之一。
评论数量越多,说明该商家受关注程度高,排名也会相应提升。
2.2.3 最近活跃度最近活跃度指商家在最近一段时间内是否有新的评论和打分。
如果商家最近有新的活动,则说明该商家仍然在运营,并且能够吸引用户关注。
最近活跃度较高的商家排名也会相应提升。
通过以上排序策略,大众点评可以将商家按照综合得分进行排序,并将排名结果展示给用户。
3. 算法调优为了提供更准确的评分和排序结果,大众点评还对评分算法进行了不断的调优。
调优的主要目标是提高算法的准确性和用户满意度。
3.1 用户反馈大众点评鼓励用户对商家进行反馈,包括评分、评论以及其他相关信息。
数学建模竞赛成绩的评价排序与预测模型

§4 一、名词解释
名词解释与符号说明
1.奖项等级:只比赛成绩划分的不同奖项,如一等奖,二等奖,三等奖,成功参 赛奖。 2.获奖比例:学校参加比赛获得某一奖项的队伍数量占所有队伍数量的比例。 3.比赛成绩:参赛队伍获得的比赛卷面成绩。 4.规模成绩:每个学校组织参赛的规模,主要包括组织参赛的队伍数量和参赛队 伍的获奖情况两个方面的因素。 5.综合实力:学校的综合实力主要是一个学校组织参赛的规模和比赛获得的奖项 状况决定的,所以学校的实力是比赛成绩与规模成绩的总和。
§3
零;
模型的假设
1.在安徽赛区的排名中, 假设专科组和本科组的记分标准一样, 不做另外分组处理; 2.假设如果一个学校那一年没有参赛, 则该年获得各个等级奖项的参赛队伍数记为 3.如果一个学校在某个奖项等级获奖空缺,也将参赛队伍记为零; 4.每年的考试难度没有差别; 5.每个同学的学习能力基本不变,并且发挥其真实水平; 6.影响学生成绩的因素主要有真实成绩与进步程度; 7.每个学生处于相同的考试环境中; 8.所给的数据时学校的真实考试成绩,没有作弊问题的影响。
n
Cj
i Wi
a
P X T N S
m ji
i
mn
优化因子 为某高校该年奖项的平均得分 为某高校该年所获奖项的总得分 为某高校该年每个学校参赛的队伍 为某高校该年所有参赛队伍的总数
§5
解。 一、问题一的分析与求解
模型的建立与求解
从所要解决的问题和对问题所做的假设出发, 分别对三个问题进行详细的分析与求
4
安徽科技学院 安徽理工大学 安徽绿海商务职业学院 安徽农业大学 安徽三联学院 安徽商贸职业技术学院 安徽师范大学 安徽新华学院 安徽新闻出版职业技术学院 安庆师范学院 蚌埠学院 亳州师范高等专科学校 巢湖学院 池州学院 滁州学院 阜阳师范学院 阜阳师范学院信息工程学院 合肥工业大学 合肥师范学院 合肥学院 河海大学文天学院 淮北师范大学 淮北师范大学信息学院 淮南联合大学 淮南师范学院 黄山学院 江淮学院 解放军电子工程学院 解放军陆军军官学院 六安职业技术学院 马鞍山师范高等专科学校 桐城师范高等专科学校 铜陵学院 皖西学院 芜湖信息技术职业学院 宿州学院 中国科学技术大学 ②年综合规模评比
评分卡模型

评分卡模型0 引言信用评分模型是消费信贷管理中的先进的技术手段,是银行、信用卡公司、个人消费信贷公司、电信公司、水电服务公司、保险公司等涉及消费信用的企业实体最核心的管理技术之一。
被广泛应用于信用卡生命周期管理、汽车贷款管理、住房贷款管理、个人贷款管理、其他消费信贷管理等领域,在市场营销、信贷审批、风险管理、账户管理、客户关系管理等各个方面都发挥十分重要的作用。
信用评分模型运用先进的数据挖掘技术和统计分析方法,通过对消费者的人口特征、信用历史记录、交易记录等大量数据进行系统的分析,挖掘数据中蕴含的行为模式、信用特征,捕捉历史信息和未来信用表现之间的关系,发展出预测性的模型,以一个信用评分来总和评估消费者未来的某种信用表现。
信用评分本质上是模式识别中的一类分类问题将企业或个体消费者划分为能够按期还本付息(即“好”客户)和违约(即“坏”客户)两类。
具体作法是根据历史上每个类别(如期还本付息、违约)的若干样本,从已知的数据中找出违约及不违约者的特征,从而总结出分类的规则,建立数学模型,用于测量借款人的违约风险(或违约概率),为消费信贷决策提供依据。
1 基于Logistic回归分析的客户信用评价卡模型本文将采用 Logistic 逻辑回归分析方法对小额贷款公司的客户信用进行评价。
首先,建立信用评价模型,给出客户信用评分卡模型,并对客户样本进行初步分类预测。
下面的理论基础和变量选择都以该小额贷款公司为例。
1.1 建模的准备1.1.1 目标变量的定义研究的目标变量为客户是否具有“违约”行为,本文是以客户逾期未归还贷款定义为“违约”行为(即“坏”客户)。
1.1.2 定量指标的筛选方法第一种定量指标的筛选方法:用随机森林法寻找自变量中对违约状态影响最显著的指标。
第二种定量指标的筛选方法:计算变量间的相对重要性,并通过相对重要性的排序,获取自变量中对违约状态影响最显著的指标。
第三种定量指标的筛选方法:通过自变量间的广义交叉验证法,获取自变量中对违约状态影响最显著的指标。
学科评价模型

答卷编号(参赛学校填写):答卷编号(竞赛组委会填写):论文题目(同时标明A、B):组别:(填写本科生、专科生):参赛队员信息:姓名专业班级及学号联系电话参赛队员1参赛队员2参赛队员3参赛学校:报名序号(可以不填):答卷编号(参赛学校填写):答卷编号(竞赛组委会填写):评阅情况(学校评阅专家填写):学校评阅1:学校评阅2:学校评阅3:评阅情况(省赛评阅专家填写):省赛评阅1:省赛评阅2:省赛评阅3:学科评价模型摘要学科间水平的评价对于学科的发展有着重要的作用,在遵循学科评价的客观性、发展性、服务性等原则的基础上,运用建模选题所提供数据,本文建立了两种不同的评价模型对学科进行评价。
模型一首先运用层次分析法确定影响学科发展的主要因素,建立指标评价体系,然后采用理想解法来建立学科评价模型;模型二与模型一一样也是运用层次分析法建立指标评价体系,然后运用专家评分法进行调查,对调查结果取众数,得到了关于学科评价指标体系各层次指标的判断矩阵,再运用matlab求判断矩阵特征值,检验判断矩阵的一致性,最终求出各指标的有效权重系数,用各指标的权重系数乘以各指标的得分,以求出学科的综合得分,得分越高,说明排在前面的指标越多,在一定程度上就是说,该学科综合实力和发展水平相对其他学科靠前。
最后,为防止有些学科中一些指标得分很高、另一些指标得分很低,但综合得分仍然靠前,而掩盖了学科发展的不稳定、不均衡的病态现象,因此,再进一步对最低级指标计算方差,以检测学科发展的稳定性和均衡性,从而指导学科的正确发展。
通过运用以上方法,不仅可以分出各学科的建设水平高低,学科本身也可看出自己发展中的优势劣势,从而,给学科发展指明了方向。
本题所提供的数据是来自科研与教学并重型高校,因此,我们在此基础上还假设了数据是来自科研型或教学型的高校,又该如何改进模型以适合不同类型的高校学科特点而给出了相应的评价模型。
关键词:学科评价层次分析法理想解法多级指标1.问题的提出学科是教学、科研等各项工作的基础和载体,学科建设水平是考察学校办学水平、办学实力、办学特色的主要标志,是高校建设的核心内容。
Borda排序法

四、方法改进
在练习中若采用 BORDA方法,以4分、3分、2分、 1分记排第一、第二、第三、第四,则各候选人的 得分为:
A : 4×18+1×31=103; B : 1×18+4×12+3×10+2×9=114; C : 2×(18+12)+4×10+3×9=127; D : 3×(18+12)+2×10+4×9=146。 D 会获最高分而当选。
(5)逐对表决。这种方法恰如单循环赛。每2位候选人 进行一次面对面的表决,共需10次,每位参加4次。 可以发现E以37比18票赢了A,以33比22票赢了B, 以36比19票赢了C,以28比27票赢了D。 E成了鹰派赢家。
例1:55位记者要在五支球队的提名代表(记为A、B、 C、D、E)中确定一位最有价值球员。现在要求每位 记者都对他们的偏爱对五名提名候选人进行排序。
55名记者的偏爱次序是:记者人数18源自12109
4
2
第一选择
A
B
C
D
E
E
第二选择
D
E
B
C
B
C
第三选择
E
D
E
E
D
D
第四选择
C
C
D
B
C
B
第五选择
B
A
A
A
A
A
解:(1)用BORDA计分法,以5、4、3、2、1分 记名次
二、评分法则
设有n个投票者,p个候选人 x1, x2 ,, x p
如果一个投票者的偏好次序为:
x1 x2 xp 则候选人 x1, x2 ,, xp 的得分依次为
一种改进的判断矩阵排序的优化模型

设 w = ( 。W , , 是正互 反判 断矩 阵 A 的最大特 征值 A 。对应 的归 一化特 征 向量 , W , … W ) ’ 即
∑z =1 ,=1 , n t , ≥0i , …, , W 2 .
若 A = ( 为完全 一致性 正互 反判 断矩 阵 , a) 则有 …
1 在 最 小 绝 对 误 差 和 准则 下 改 进 的 判 断矩 阵排 序 的 优化 模 型 的建 立
设 矩 阵 A : ( … 是 n阶正互 反判 断矩 阵 , A 满足 : a) 即
a > 0, = 1 a = 1 a ̄ V i = 1, … , i≠ . a , /j , 2, n,
一
种 改 进 的 判 断 矩 阵 排 序 的 优 化 模 型
胡 彦。 张俊 婷 陈 一, ,
( 安徽 大学 a .数 学 科 学 学 院 , 肥 合
诚
20 1 ) 30 1
203 ; . 30 9 b 职业 技 术 学 院 , 合肥
摘
要: 层次分析法是一种重要的多属性决策方法, 如何判 断矩 阵的构造及其 给 出合理 的排序方 法是其研 究的
() 3
由于判 断矩 阵是 由决 策者 给 出的 , 以决策 者 的知识水 平 、 验 和偏 好等 主观 因素必 然影 响判断一 致 所 经
性 .若 A 为非一致 性判 断矩 阵 , 3 ( )式 的等式 不可 能恒成 立. 合理 的权 系数 向量 W应该 使其 到所有平 面 故
距 离最 短.’到第 i 平面 的欧 氏距离 . , 个
Aw —n =0 w .
() 1
() 2
注意 到 A = ( ' a ) … . ( W , , )’ ( ) ,= W , … , 1 式写 成矩 阵形式 为
als算法与apS

als算法与apSALS(Alternating Least Squares)算法和APS(Approximate Personalized Ranking)算法都是用来解决协同过滤推荐问题的算法,但在实现上有一些不同之处。
ALS算法是一种基于矩阵分解的协同过滤方法,主要用于解决推荐系统中的矩阵填充问题。
其基本思想是将用户-物品评分矩阵分解成两个低秩矩阵的乘积,然后通过交替更新这两个矩阵的行向量来优化模型。
具体而言,算法分为两个步骤:首先,固定用户向量,通过最小化误差函数来求解物品向量;其次,固定物品向量,通过最小化误差函数来求解用户向量。
通过不断迭代这两个步骤,最终得到的用户和物品的向量即为推荐系统的模型。
与ALS算法不同,APS算法是一种基于代价函数最小化的协同过滤算法,主要应用于推荐系统中的个性化排序。
其基本思想是将用户个性化排序问题转化为一个排序问题,并通过最小化排序代价函数来优化模型。
具体实现上,APS算法将用户-物品评分矩阵分解成两个低秩矩阵的乘积,并引入了排序代价函数。
通过迭代更新矩阵的行向量,使得排序代价函数最小化,从而优化模型。
APS算法的优点是能够更好地处理排名问题,适用于个性化排序场景。
两种算法的主要区别在于应用场景和优化目标。
ALS算法主要应用于填充用户-物品评分矩阵的问题,通过矩阵分解来优化模型。
而APS算法主要应用于个性化排序问题,将用户-物品评分矩阵转化为排序代价函数最小化的问题。
此外,ALS算法的优化目标是最小化误差函数,而APS算法的优化目标是最小化排序代价函数。
在实际应用中,选择使用ALS算法还是APS算法要根据具体场景和需求来决定。
如果需要填充用户-物品评分矩阵并进行推荐,可以选择ALS 算法;如果需要进行个性化排序,推荐系统中的物品展示顺序需要个性化定制,可以选择APS算法。
此外,还可以根据实际情况来选择不同的调参策略和性能优化方法,以提高算法的推荐效果和运行效率。
【经典】建模-组合优化模型-排序问题
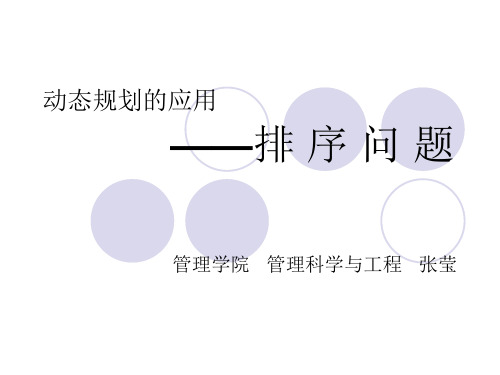
(X,t) (X/{i,j},zij(t))
f (X ,t,i, j) ai aj f [X /i, j, zij(t)]
zij (t ) max[zi(t) aj,0] bj max(t ai aj bi bj, bi bj aj, bj)
zji (t ) max( t ai aj bi bj, bi bj ai, bi)
ai f (X / i,t ai bi) 当t ai时
f (X ,t,i)
ai f (X / i,bi)
当t ai时
zi(t) max( t ai,0) bi f ( X , t, i) ai f [ X / i, zi(t)]
X/i表示在集合X中去掉工件i后剩下的工件集合
5
6
8
+2
+2
-5
9
5ቤተ መጻሕፍቲ ባይዱ
43
2
T
动态规划思想
动态规划是用来解决多阶段决策过程最优 化的一种数量方法。其特点在于,它可以 把一个n 维决策问题变换为几个一维最优 化问题,从而一个一个地去解决。
需指出:动态规划是求解某类问题的一种 方法,是考察问题的一种途径,而不是一 种算法。必须对具体问题进行具体分析, 运用动态规划的原理和方法,建立相应的 模型,然后再用动态规划方法去求解。
j2
j3
j4
j5
7
1
5
4
交货日期(d) 23
20
8
6
14
分析:
加工工件在机床A上有加工顺序问题,在机
床B上也有加工顺序问题。可以证明:最优 排序方案可以只在机床A、B上加工顺 序相同的排序中寻找。即使如此,所有
可能的方案仍有n!个,这是一个不小的数, 用穷举法是不现实的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
评分排序优化模型摘要一年一度的全国大学生数学建模竞赛,是一项规模宏大的课外科技活动之一。
所给问题要求建立一个评分排序优化模型,正是针对建模竞赛中重要环节——答卷评分排序环节而提出的,具有很重要的实际应用意义。
答卷的评分排序只有做到科学、合理、公正,才能评选出优秀的作品。
根据这些特点,我们对所给问题运用统计数学中的统计学原理建立模型,由简单到复杂,由片面到均衡兼顾,逐步优化。
建模前期,我们对所给数据进行了筛选,部分答卷为零分或只有两个数据,也许违反了竞赛规则和评阅规则,将作为废卷处理,剔除这一小部分答卷的数据。
首先,我们建立了常用的简单模型I ——均值评比模型,其数学表达式为913jij i xP ==∑,得到最初的名次,前五名的答卷编号分别为。
然后,考虑到模型I忽略了不同评委对同一份答卷的差异,及评委的自身知识水平的限制和主观成份的波动误差影响,结果存在很大的误差。
在对均值评比模型改进的基础上建立了模型II ——标准分模型。
其数学表达式为90013ji j j j i x x x s P δ=⎛⎫-⋅+ ⎪ ⎪⎝⎭=∑,由于该模型成立的前提条件是服从正态分布,故借助SPSS 对数据进行了单样本K-S 正态检验和描述性统计分析,可得每位评委的评分服从正态分布及相关统计数据,使用MATLAB 软件编程计算出所有评分的标准分,再利用模型I 求出均值,进行名次排序,前五名的答卷编号分别为。
其次,对数据进行单因素方差分析,可得各评委的评分偏好存在较大的差异,给每位评委加权,建立了模型III ——加权评分模型,其数学表达式为()000,100100100,100ji j jji jx x x x x i x x P ⋅≤-⋅-+-⎧⎪=⎨⎪⎩当时否则利用MATLAB 软件编程求解出所有加权后的评分,依旧用模型I 求出均值,进行名次排序,得到新的名次,前五名的答卷编号分别为。
最后,对三个模型进行评价,并对其结果进行对比分析。
关键词:均值、正态检验、描述性统计、标准化、单因素分析、加权目录一、问题重述 (3)二、问题分析 (3)三、模型的假设 (4)四、符号的定义 (5)五、模型的建立与求解 (6)第一部分准备工作……………………………………第二部分建立评分排序优化模型……………………(一) 模型I——均值评比模型 (8)(二) 模型Ⅱ——标准分模型………………………(三) 模型Ⅲ——加权评分模型……………………六、结果分析……………………………………………………七、模型的评价与推广 (10)八、参考文献 (11)九、附录…………………………………………………………评分排序优化模型一、问题重述全国大学生数学建模竞赛是全国高校规模最大的课外科技活动之一,评卷是其中一个至关重要的环节。
评卷以假设的合理性、建模的创造性、结果的正确性和文字表述的清晰程度为主要标准。
对同一问题,给参赛者提供了较大的创新空间,运用不同的数学知识和方法,建立数学模型。
同时也给评卷工作带来一定的难度。
尽管评卷者大都为建模方面的专家,但由于各自研究方向的局限、对某些理论理解程度的不同,常常会在评阅中带有主观的成份,造成对同一答卷评判会略有差异。
如何根据每个专家的评分,公正合理地评选出优秀的作品,是一个值得研究的问题。
评卷工作的评委由该赛区竞赛组委会聘请(指定),通常为该赛区高校教师。
为保证评卷工作的准确、公平、合理,对评委除了专业能力的要求外,制定了如下评卷规则:(1)评委不能是该校本年度数学建模比赛的指导教师。
(2)评阅每题的评委人数根据答卷的多少按比例分配,但不能少于三人。
(3)评阅采取回避制,评委不能评阅本校的参赛论文。
(4)保证每份答卷有三人评阅。
赛区在评阅前,对所有的论文进行编号,论文中没有任何可能显示答题人身份的标志,并根据上述的评卷规则,把论文分派给每位评委。
表1为某赛区B题各评委的按照事先的评分标准评出的成绩。
根据这些资料,利用数学建模的方法,给答卷一个科学、合理、公正的排序,以便评出优秀的作品。
二、问题分析主要是表达对题目的理解,特别是对附件的数据进行必要分析、描述(一般都有数据附件),这是需要提到分析数据的方法、理由。
评分排序优化问题研究有非常重要的意义。
全国大学生数学建模竞赛是一种大型的重大赛事,评分的科学、合理、公正更是尤为重要,只有做到科学、合理、公正,才能真正体现这种大型竞赛的价值。
而评委自身的知识领域局限和主观成分对评分造成的偏差无可避免,建立一种评分排序优化模型,以消除或减少评委的系统误差带来的对参赛队成绩影响,很有实际运用意义。
评分排序优化问题属于数理统计中优化综合评比的数学问题,对于解决此类问题要用数理统计的相关原理进行分析,建立模型。
附件所给数据是195份答卷所有评分的原始数据,总共有9位评委参与评卷,根据评卷规则,每份答卷由三位评委评阅并给原始评分。
可能由于作弊抄袭等原因,有14份答卷全为零分,考虑这小部分答卷的数据对总体数据分析影响不大,因此视为废卷,剔除这部分数据。
我们用单样本K-S正态检验、描述性统计分析和单因素方差分析等方法进行数据分析。
首先,我们建立一个简单的直接取平均分的数学模型I,然后考虑评委自身限制和主观因素影响,将所有评委的评分转化到统一价值尺度中,建立一个标准分模型II,根据每位评委评分偏好的不一致性,为减少这种不一致性带来的误差,将建立加权评分模型III,根据每个模型求出每份答卷的最终成绩,进行排序,并将结果进行比较分析.三、模型假设1. 假设每份答卷都有绝对分数,能够反映其真实水平,且每份答卷分数服从正态分布;2.假设每位评委所评分数服从正态分布;3.假设每名评委独立评卷,互不影响;4.假设每名评委的评分偏差服从以他的尺度偏差为期望的正态分布。
5. 假设答卷的分数制度为百分制。
四、符号定义j N :第j 位评委的评阅卷数ji x :第j 位评委对第i 份答卷的评分,规定当第j 位评委不对第i 份答卷评分时,ji x =0j x :第j 位评委评分的均值j s :第j 位评委评分的标准差i P :第i 份答卷的综合评分ji Z :第j 位评委对第i 份答卷的评分标准化后的评分0x :所有答卷评分的均值0 :所有答卷评分的的标准差五、模型的建立与求解第一部分:准备工作 (一)数据的处理1、答卷编号B004、B015、B019、B034、B060、B064、B067、B076、B091、B094、B144、B148、B157、B185数据全部缺失,或由于抄袭等原因所有评分都给了零分,故将其 视为废卷,不予考虑。
2、答卷编号B158数据残缺,只有两个评委的评分,不符合保证每份答卷有三人评阅的评卷规则,或某位评委发现该份答卷违反了竞赛规则,评为零分,将其视为废卷,不予考虑。
3、剔除废卷后的数据有如下特点:①每份答卷按照竞赛评卷规则评阅人数都为3人;②九位评委都参与了评阅,但每份答卷对应的评委无明显的一致性,也就是说相同的三位评委一起评阅多份答卷的概率不大,数据较分散。
(二)单样本K-S 正态检验:用SPSS 软件检验每位评委的评分服从正态分布。
(三)描述性统计分析:用SPSS 软件描述性统计分析,将每位评委所对应的特征值进行列表。
(四)单因素方差分析:用MATLAB 的anova1命令分析比较9位评委的评分偏好及评分离散程度。
(五)预测的准备工作:根据数据特点,对总体和个体的特点进行比较,以表格或图示方式显示。
第二部分:建立评分排序优化模型(一)模型I ——均值评比模型1.模型I 的数学表达式:913jij i xP ==∑该模型是一般的常规比赛中最常用的成绩评判方法,对多组成绩采用直接平均的方法即得最终成绩。
2. 模型I 的求解利用办公软件Excel 对数据进行求和取平均、排序,即得所有答卷在模型I 下的排名。
3.模型I 的评价模型I 是最简单快捷的成绩评定办法,但存在很大的缺陷,就是忽略了评委的主观成分对评分的影响,造成很大的误差,成绩均值并未能真正反映其真实水平。
因此,需要综合考虑评委自身知识水平的限制及主观成分的影响,下面将对所有评分进行标准化处理,我们建立了模型II.(二)模型Ⅱ——标准分模型由于每一个评委给出的分数体现不同试卷在他心中的排名的差异,那么把分数整体平移是不会改变这种差异的。
根据文献[3]的思想,就可以得到模型Ⅱ,即将每位评卷老师的均值平移到同一个基点,这个基点我们选取所以老师所给出的分数的均值。
而每位老师方差的不同导致每位老师所给出的每一分对总分的贡献不同,因此我们把所有老师的离散(即方差)调到同一水平,这个水平我们就选取所有老师方差的均值,于是模型Ⅱ就更能体现评卷的公平性1.建立模型Ⅱ前的准备:每位评委评分分布的正态性检验由上表可得,每位评委的显著性水平(P 值)都大于0.05,因此每位评委的评分服从正态分布。
2.模型Ⅱ的数学表达式如下:ji jji jx x Z s -=(18011j jii jx xN ==∑,j s =由于标准化后的数会出现负数和小数点,使用起来不方便,因此再对标准化后的Z 分数进行T 分数变换:00ji ji T Z x δ=⋅+取均值: 913jij i TP ==∑模型Ⅱ的总数学表达式为90013ji jj j i x x x s P δ=⎛⎫-⋅+ ⎪ ⎪⎝⎭=∑3.模型Ⅱ的求解 (1)借助SPSS 软件对数据进行描述性统计分析,可得每位评委的评阅卷数、评分的最小值和最大值、均值、标准差,直接使用操作命令,既简单又快捷,省去用其他软件编程的麻烦。
执行后结果如下:(2)利用MATLAB 软件编程求解求总体评分均值0x 、标准差0δ:导入数据→剔除废卷数据→所有评分化为一向量→使用mean 、std 命令。
运行结果为 045.6500x =,09.7656δ=(三)模型Ⅲ——加权评分模型 1.建立模型Ⅲ前的准备通过单因素方差分析比较9位评委的评分偏好在MATLAB 中的调用格式:P=anova1(X) X 为数据矩阵 具体程序见附录 运行结果:P=0ANOVA Table∙ Source SS df MS F Prob>F ∙ -------------------------------------------------------------------------------------------------------- ∙Groups 11379.8 8 1422.48 18.87 0∙ Error 40023 531 75.37 ∙ Total 51402.8 539结果分析可得,对同一份答卷,不同评委的评分差异影响显著。
图形分析:该图显示了这9位评委的评分分散情况,和最值、均值的粗略位置,评分分散程度最大的是评委5,最小的是评委6,对于评分偏好,评委4和评委9的评分偏低,评委5的评分偏高,其他评委在评分居中线上上下波动,虽有差异,但不是相差很大。
