初二压轴题特殊的平行四边形
中考数学与平行四边形有关的压轴题含答案解析
本题考查四边形综合题、等腰直角三角形的判定和性质、等边三角形的判定和性质、等腰三角形的性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题.
7.(1)问题发现:
如图①,在等边三角形ABC中,点M为BC边上异于B、C的一点,以AM为边作等边三角形AMN,连接CN,NC与AB的位置关系为;
6.问题情境
在四边形ABCD中,BA=BC,DC⊥AC,过点D作DE∥AB交BC的延长线于点E,M是边AD的中点,连接MB,ME.
特例探究
(1)如图1,当∠ABC=90°时,写出线段MB与ME的数量关系,位置关系;
(2)如图2,当∠ABC=120°时,试探究线段MB与ME的数量关系,并证明你的结论;
∴∠DEC=90°,
∴∠DCE=∠CDE=45°,
∴EC=ED,∵MC=MD,
∴EM垂直平分线段CD,EM平分∠DEC,
∴∠MEC=45°,
∴△BME是等腰直角三角形,
∴BM=ME,BM⊥EM.
故答案为BM=ME,BM⊥EM.
(2)ME= MB.
证明如下:连接CM,如解图所示.
∵DC⊥AC,M是边AD的中点,
∴ AB•CF= AC•PE﹣ AB•PD.
∵AB=AC,
∴CF=PD﹣PE;
结论运用:过点E作EQ⊥BC,垂足为Q,如图④,
∵四边形ABCD是长方形,
∴AD=BC,∠C=∠ADC=90°.
∵AD=16,CF=6,
∴BF=BC﹣CF=AD﹣CF=5,
由折叠可得:DF=BF,∠BEF=∠DEF.
∴DF=5.
∴PG+PH的值为8;
迁移拓展:如图,
由题意得:A(0,8),B(6,0),C(﹣4,0)
2020-2021备战中考数学压轴题专题复习——平行四边形的综合含答案

2020-2021备战中考数学压轴题专题复习——平行四边形的综合含答案一、平行四边形1.如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.(1)求证:AD=EC;(2)当∠BAC=Rt∠时,求证:四边形ADCE是菱形.【答案】(1)见解析;(2)见解析.【解析】【分析】(1)先证四边形ABDE是平行四边形,再证四边形ADCE是平行四边形即可;(2)由∠BAC=90°,AD是边BC上的中线,得AD=BD=CD,即可证明.【详解】(1)证明:∵AE∥BC,DE∥AB,∴四边形ABDE是平行四边形,∴AE=BD,∵AD是边BC上的中线,∴BD=DC,∴AE=DC,又∵AE∥BC,∴四边形ADCE是平行四边形.(2) 证明:∵∠BAC=90°,AD是边BC上的中线.∴AD=CD∵四边形ADCE是平行四边形,∴四边形ADCE是菱形.【点睛】本题考查了平行四边形的判定、菱形的判定、直角三角形斜边中线定理.根据图形与已知条件灵活应用平行四边形的判定方法是证明的关键.2.如图(1)在正方形ABCD中,点E是CD边上一动点,连接AE,作BF⊥AE,垂足为G 交AD于F(1)求证:AF=DE;(2)连接DG,若DG平分∠EGF,如图(2),求证:点E是CD中点;(3)在(2)的条件下,连接CG,如图(3),求证:CG=CD.【答案】(1)见解析;(2)见解析;(3)CG=CD,见解析.【解析】【分析】(1)证明△BAF≌△ADE(ASA)即可解决问题.(2)过点D作DM⊥GF,DN⊥GE,垂足分别为点M,N.想办法证明AF=DF,即可解决问题.(3)延长AE,BC交于点P,由(2)知DE=CD,利用直角三角形斜边中线的性质,只要证明BC=CP即可.【详解】(1)证明:如图1中,在正方形ABCD中,AB=AD,∠BAD=∠D=90o,∴∠2+∠3=90°又∵BF⊥AE,∴∠AGB=90°∴∠1+∠2=90°,∴∠1=∠3在△BAF与△ADE中,∠1=∠3 BA=AD ∠BAF=∠D,∴△BAF≌△ADE(ASA)∴AF=DE.(2)证明:过点D作DM⊥GF,DN⊥GE,垂足分别为点M,N.由(1)得∠1=∠3,∠BGA=∠AND=90°,AB=AD ∴△BAG≌△ADN(AAS)∴AG=DN,又DG平分∠EGF,DM⊥GF,DN⊥GE,∴DM=DN,∴DM=AG,又∠AFG=∠DFM,∠AGF=∠DMF∴△AFG≌△DFM(AAS),∴AF=DF=DE=12AD=12CD,即点E是CD的中点.(3)延长AE,BC交于点P,由(2)知DE=CD,∠ADE=∠ECP=90°,∠DEA=∠CEP,∴△ADE≌△PCE(ASA)∴AE=PE,又CE∥AB,∴BC=PC,在Rt△BGP中,∵BC=PC,∴CG=12BP=BC,∴CG=CD.【点睛】本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,角平分线的性质定理,直角三角形斜边中线的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.3.(1)如图①,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,交AD 于点E ,交BC 于点F ,连接BE 、DF ,且BE 平分∠ABD .①求证:四边形BFDE 是菱形;②直接写出∠EBF 的度数;(2)把(1)中菱形BFDE 进行分离研究,如图②,点G 、I 分别在BF 、BE 边上,且BG=BI ,连接GD ,H 为GD 的中点,连接FH 并延长,交ED 于点J ,连接IJ 、IH 、IF 、IG.试探究线段IH 与FH 之间满足的关系,并说明理由;(3)把(1)中矩形ABCD 进行特殊化探究,如图③,当矩形ABCD 满足AB=AD 时,点E 是对角线AC 上一点,连接DE 、EF 、DF ,使△DEF 是等腰直角三角形,DF 交AC 于点G.请直接写出线段AG 、GE 、EC 三者之间满足的数量关系.【答案】(1)①详见解析;②60°.(2)IH =3FH ;(3)EG 2=AG 2+CE 2.【解析】【分析】(1)①由△DOE ≌△BOF ,推出EO =OF ,∵OB =OD ,推出四边形EBFD 是平行四边形,再证明EB =ED 即可.②先证明∠ABD =2∠ADB ,推出∠ADB =30°,延长即可解决问题.(2)IH =3FH .只要证明△IJF 是等边三角形即可.(3)结论:EG 2=AG 2+CE 2.如图3中,将△ADG 绕点D 逆时针旋转90°得到△DCM ,先证明△DEG ≌△DEM ,再证明△ECM 是直角三角形即可解决问题.【详解】(1)①证明:如图1中,∵四边形ABCD 是矩形,∴AD ∥BC ,OB =OD ,∴∠EDO =∠FBO ,在△DOE 和△BOF 中,EDO FBO OD OBEOD BOF ∠∠⎧⎪⎨⎪∠∠⎩=== , ∴△DOE ≌△BOF ,∴EO =OF ,∵OB =OD ,∴四边形EBFD 是平行四边形,∵EF ⊥BD ,OB =OD ,∴EB =ED ,∴四边形EBFD 是菱形.②∵BE 平分∠ABD ,∴∠ABE =∠EBD ,∵EB =ED ,∴∠EBD =∠EDB ,∴∠ABD =2∠ADB ,∵∠ABD +∠ADB =90°,∴∠ADB =30°,∠ABD =60°,∴∠ABE =∠EBO =∠OBF =30°,∴∠EBF =60°.(2)结论:IH=3FH .理由:如图2中,延长BE 到M ,使得EM =EJ ,连接MJ .∵四边形EBFD 是菱形,∠B =60°,∴EB =BF =ED ,DE ∥BF ,∴∠JDH =∠FGH ,在△DHJ 和△GHF 中,DHG GHF DH GHJDH FGH ∠∠⎧⎪⎨⎪∠∠⎩=== , ∴△DHJ ≌△GHF ,∴DJ =FG ,JH =HF ,∴EJ =BG =EM =BI ,∴BE =IM =BF ,∵∠MEJ =∠B =60°,∴△MEJ 是等边三角形,∴MJ =EM =NI ,∠M =∠B =60°在△BIF 和△MJI 中,BI MJ B M BF IM ⎧⎪∠∠⎨⎪⎩===,∴△BIF ≌△MJI ,∴IJ =IF ,∠BFI =∠MIJ ,∵HJ =HF ,∴IH ⊥JF ,∵∠BFI +∠BIF =120°,∴∠MIJ +∠BIF =120°,∴∠JIF =60°,∴△JIF 是等边三角形,在Rt △IHF 中,∵∠IHF =90°,∠IFH =60°,∴∠FIH =30°,∴IH=3FH .(3)结论:EG 2=AG 2+CE 2.理由:如图3中,将△ADG 绕点D 逆时针旋转90°得到△DCM ,∵∠FAD +∠DEF =90°,∴AFED 四点共圆,∴∠EDF =∠DAE =45°,∠ADC =90°,∴∠ADF +∠EDC =45°,∵∠ADF =∠CDM ,∴∠CDM +∠CDE =45°=∠EDG ,在△DEM 和△DEG 中,DE DE EDG EDM DG DM ⎧⎪∠∠⎨⎪⎩=== , ∴△DEG ≌△DEM ,∴GE =EM ,∵∠DCM =∠DAG =∠ACD =45°,AG =CM ,∴∠ECM =90°∴EC 2+CM 2=EM 2,∵EG =EM ,AG =CM ,∴GE 2=AG 2+CE 2.【点睛】考查四边形综合题、矩形的性质、正方形的性质、菱形的判定和性质,等边三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,学会转化的思想思考问题.4.如图,在平行四边形ABCD 中,AD ⊥DB ,垂足为点D ,将平行四边形ABCD 折叠,使点B落在点D的位置,点C落在点G的位置,折痕为EF,EF交对角线BD于点P.(1)连结CG,请判断四边形DBCG的形状,并说明理由;(2)若AE=BD,求∠EDF的度数.【答案】(1)四边形BCGD是矩形,理由详见解析;(2)∠EDF=120°.【解析】【分析】(1)根据平行四边形的性质和折叠性质以及矩形的判定解答即可;(2)根据折叠的性质以及直角三角形的性质和等边三角形的判定与性质解答即可.【详解】解:(1)四边形BCGD是矩形,理由如下,∵四边形ABCD是平行四边形,∴BC∥AD,即BC∥DG,由折叠可知,BC=DG,∴四边形BCGD是平行四边形,∵AD⊥BD,∴∠CBD=90°,∴四边形BCGD是矩形;(2)由折叠可知:EF垂直平分BD,∴BD⊥EF,DP=BP,∵AD⊥BD,∴EF∥AD∥BC,∴AE PD1==BE BP∴AE=BE,∴DE是Rt△ADB斜边上的中线,∴DE=AE=BE,∵AE=BD,∴DE=BD=BE,∴△DBE是等边三角形,∴∠EDB=∠DBE=60°,∵AB∥DC,∴∠DBC=∠DBE=60°,∴∠EDF=120°.【点睛】本题考查了平行四边形的性质,折叠性质,等边三角形的性质和判定,主要考查学生运用定理进行推理和计算的能力,题目综合性比较强,有一定的难度5.已知AD是△ABC的中线P是线段AD上的一点(不与点A、D重合),连接PB、PC,E、F、G、H分别是AB、AC、PB、PC的中点,AD与EF交于点M;(1)如图1,当AB=AC时,求证:四边形EGHF是矩形;(2)如图2,当点P与点M重合时,在不添加任何辅助线的条件下,写出所有与△BPE面积相等的三角形(不包括△BPE本身).【答案】(1)见解析;(2)△APE、△APF、△CPF、△PGH.【解析】【分析】(1)由三角形中位线定理得出EG∥AP,EF∥BC,EF=12BC,GH∥BC,GH=12BC,推出EF∥GH,EF=GH,证得四边形EGHF是平行四边形,证得EF⊥AP,推出EF⊥EG,即可得出结论;(2)由△APE与△BPE的底AE=BE,又等高,得出S△APE=S△BPE,由△APE与△APF的底EP=FP,又等高,得出S△APE=S△APF,由△APF与△CPF的底AF=CF,又等高,得出S△APF=S△CPF,证得△PGH底边GH上的高等于△AEF底边EF上高的一半,推出S△PGH=12S△AEF=S△APF,即可得出结果.【详解】(1)证明:∵E、F、G、H分别是AB、AC、PB、PC的中点,∴EG∥AP,EF∥BC,EF=12BC,GH∥BC,GH=12BC,∴EF∥GH,EF=GH,∴四边形EGHF是平行四边形,∵AB=AC,∴AD⊥BC,∴EF⊥AP,∵EG∥AP,∴EF⊥EG,∴平行四边形EGHF是矩形;(2)∵PE是△APB的中线,∴△APE与△BPE的底AE=BE,又等高,∴S△APE=S△BPE,∵AP是△AEF的中线,∴△APE与△APF的底EP=FP,又等高,∴S△APE=S△APF,∴S△APF=S△BPE,∵PF是△APC的中线,∴△APF与△CPF的底AF=CF,又等高,∴S△APF=S△CPF,∴S△CPF=S△BPE,∵EF∥GH∥BC,E、F、G、H分别是AB、AC、PB、PC的中点,∴△AEF底边EF上的高等于△ABC底边BC上高的一半,△PGH底边GH上的高等于△PBC 底边BC上高的一半,∴△PGH底边GH上的高等于△AEF底边EF上高的一半,∵GH=EF,∴S△PGH=12S△AEF=S△APF,综上所述,与△BPE面积相等的三角形为:△APE、△APF、△CPF、△PGH.【点睛】本题考查了矩形的判定与性质、平行四边形的判定、三角形中位线定理、平行线的性质、三角形面积的计算等知识,熟练掌握三角形中位线定理是解决问题的关键.6.如图,在平面直角坐标系中,直线DE交x轴于点E(30,0),交y轴于点D(0,40),直线AB:y=13x+5交x轴于点A,交y轴于点B,交直线DE于点P,过点E作EF⊥x轴交直线AB于点F,以EF为一边向右作正方形EFGH.(1)求边EF的长;(2)将正方形EFGH沿射线FB10个单位的速度匀速平移,得到正方形E1F1G1H1,在平移过程中边F1G1始终与y轴垂直,设平移的时间为t秒(t>0).①当点F1移动到点B时,求t的值;②当G1,H1两点中有一点移动到直线DE上时,请直接写出此时正方形E1F1G1H1与△APE重叠部分的面积.【答案】(1)EF=15;(2)①10;②120;【解析】【分析】(1)根据已知点E(30,0),点D(0,40),求出直线DE的直线解析式y=-43x+40,可求出P点坐标,进而求出F点坐标即可;(2)①易求B(0,5),当点F1移动到点B时,1010=10;②F点移动到F'10t,F垂直x轴方向移动的距离是t,当点H运动到直线DE上时,在Rt△F'NF中,NFNF'=13,EM=NG'=15-F'N=15-3t,在Rt△DMH'中,43MHEM'=,t=4,S=12×(12+454)×11=10238;当点G运动到直线DE上时,在Rt△F'PK中,PKF K'=13,PK=t-3,F'K=3t-9,在Rt△PKG'中,PKKG'=31539tt--+=43,t=7,S=15×(15-7)=120.【详解】(1)设直线DE的直线解析式y=kx+b,将点E(30,0),点D(0,40),∴30040k bb+=⎧⎨=⎩,∴4340kb⎧=-⎪⎨⎪=⎩,∴y=﹣43x+40,直线AB与直线DE的交点P(21,12),由题意知F(30,15),∴EF=15;(2)①易求B(0,5),∴BF=10,∴当点F 1移动到点B 时,t =101010÷=10; ②当点H 运动到直线DE 上时,F 点移动到F'的距离是10t ,在Rt △F'NF 中,NF NF '=13, ∴FN =t ,F'N =3t ,∵MH'=FN =t ,EM =NG'=15﹣F'N =15﹣3t ,在Rt △DMH'中,43MH EM '=, ∴41533t t =-, ∴t =4, ∴EM =3,MH'=4,∴S =1451023(12)11248⨯+⨯=; 当点G 运动到直线DE 上时,F 点移动到F'10,∵PF =10∴PF'10t ﹣10,在Rt △F'PK 中,13PK F K =', ∴PK =t ﹣3,F'K =3t ﹣9,在Rt △PKG'中,PK KG '=31539t t --+=43, ∴t =7,∴S =15×(15﹣7)=120.【点睛】本题考查一次函数图象及性质,正方形的性质;掌握待定系数法求函数解析式,利用三角形的正切值求边的关系,利用勾股定理在直角三角形中建立边之间的联系,准确确定阴影部分的面积是解题的关键.7.如图所示,矩形ABCD 中,点E 在CB 的延长线上,使CE =AC ,连接AE ,点F 是AE 的中点,连接BF 、DF ,求证:BF ⊥DF .【答案】见解析.【解析】【分析】延长BF ,交DA 的延长线于点M ,连接BD ,进而求证△AFM ≌△EFB ,得AM =BE ,FB =FM ,即可求得BC +BE =AD +AM ,进而求得BD =BM ,根据等腰三角形三线合一的性质即可求证BF ⊥DF .【详解】延长BF ,交DA 的延长线于点M ,连接BD .∵四边形ABCD 是矩形,∴MD ∥BC ,∴∠AMF =∠EBF ,∠E =∠MAF ,又FA =FE ,∴△AFM ≌△EFB ,∴AM =BE ,FB =FM .∵矩形ABCD 中,∴AC =BD ,AD =BC ,∴BC +BE =AD +AM ,即CE =MD .∵CE =AC ,∴AC =CE = BD =DM .∵FB =FM ,∴BF ⊥DF .【点睛】本题考查了矩形的性质,全等三角形的判定和对应边相等的性质,等腰三角形三线合一的性质,本题中求证DB =DM 是解题的关键.8.如图,现将平行四边形ABCD沿其对角线AC折叠,使点B落在点B′处.AB′与CD交于点E.(1)求证:△AED≌△CEB′;(2)过点E作EF⊥AC交AB于点F,连接CF,判断四边形AECF的形状并给予证明.【答案】(1)见解析(2)见解析【解析】【分析】(1)由题意可得AD=BC=B'C,∠B=∠D=∠B',且∠AED=∠CEB',利用AAS证明全等,则结论可得;(2)由△AED≌△CEB′可得AE=CE,且EF⊥AC,根据等腰三角形的性质可得EF垂直平分AC,∠AEF=∠CEF.即AF=CF,∠CEF=∠AFE=∠AEF,可得AE=AF,则可证四边形AECF是菱形.【详解】证明:(1)∵四边形ABCD是平行四边形∴AD=BC,CD∥AB,∠B=∠D∵平行四边形ABCD沿其对角线AC折叠∴BC=B'C,∠B=∠B'∴∠D=∠B',AD=B'C且∠DEA=∠B'EC∴△ADE≌△B'EC(2)四边形AECF是菱形∵△ADE≌△B'EC∴AE=CE∵AE=CE,EF⊥AC∴EF垂直平分AC,∠AEF=∠CEF∴AF=CF∵CD∥AB∴∠CEF=∠EFA且∠AEF=∠CEF∴∠AEF=∠EFA∴AF=AE∴AF=AE=CE=CF∴四边形AECF是菱形【点睛】本题考查了折叠问题,全等三角形的判定和性质,平行四边形的性质,菱形的判定,熟练掌握这些性质和判定是解决问题的关键.9.问题情境在四边形ABCD 中,BA =BC ,DC ⊥AC ,过点D 作DE ∥AB 交BC 的延长线于点E ,M 是边AD 的中点,连接MB ,ME.特例探究(1)如图1,当∠ABC =90°时,写出线段MB 与ME 的数量关系,位置关系;(2)如图2,当∠ABC =120°时,试探究线段MB 与ME 的数量关系,并证明你的结论; 拓展延伸(3)如图3,当∠ABC =α时,请直接用含α的式子表示线段MB 与ME 之间的数量关系.【答案】(1)MB =ME ,MB ⊥ME ;(2)ME =3MB .证明见解析;(3)ME =MB·tan 2α. 【解析】【分析】(1)如图1中,连接CM .只要证明△MBE 是等腰直角三角形即可;(2)结论:EM=3MB .只要证明△EBM 是直角三角形,且∠MEB=30°即可; (3)结论:EM=BM•tan2α.证明方法类似; 【详解】(1) 如图1中,连接CM .∵∠ACD=90°,AM=MD ,∴MC=MA=MD ,∵BA=BC ,∴BM 垂直平分AC ,∵∠ABC=90°,BA=BC ,∴∠MBE=12∠ABC=45°,∠ACB=∠DCE=45°, ∵AB ∥DE ,∴∠ABE+∠DEC=180°,∴∠DEC=90°,∴∠DCE=∠CDE=45°,∴EC=ED ,∵MC=MD ,∴EM 垂直平分线段CD ,EM 平分∠DEC ,∴∠MEC=45°,∴△BME 是等腰直角三角形,∴BM=ME ,BM ⊥EM .故答案为BM=ME ,BM ⊥EM .(2)ME =3MB .证明如下:连接CM ,如解图所示.∵DC ⊥AC ,M 是边AD 的中点,∴MC =MA =MD .∵BA =BC ,∴BM 垂直平分AC .∵∠ABC =120°,BA =BC ,∴∠MBE =12∠ABC =60°,∠BAC =∠BCA =30°,∠DCE =60°. ∵AB ∥DE ,∴∠ABE +∠DEC =180°,∴∠DEC =60°,∴∠DCE =∠DEC =60°,∴△CDE 是等边三角形,∴EC =ED .∵MC =MD ,∴EM 垂直平分CD ,EM 平分∠DEC , ∴∠MEC =12∠DEC =30°, ∴∠MBE +∠MEB =90°,即∠BME =90°.在Rt △BME 中,∵∠MEB =30°,∴ME 3.(3) 如图3中,结论:EM=BM•tan 2.理由:同法可证:BM ⊥EM ,BM 平分∠ABC ,所以EM=BM•tan 2. 【点睛】本题考查四边形综合题、等腰直角三角形的判定和性质、等边三角形的判定和性质、等腰三角形的性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题.10.在矩形纸片ABCD 中,AB=6,BC=8,现将纸片折叠,使点D 与点B 重合,折痕为EF ,连接DF .(1)说明△BEF 是等腰三角形;(2)求折痕EF 的长.【答案】(1)见解析;(2).【解析】【分析】 (1)根据折叠得出∠DEF =∠BEF ,根据矩形的性质得出AD ∥BC ,求出∠DEF =∠BFE ,求出∠BEF =∠BFE 即可;(2)过E 作EM ⊥BC 于M ,则四边形ABME 是矩形,根据矩形的性质得出EM =AB =6,AE =BM ,根据折叠得出DE =BE ,根据勾股定理求出DE 、在Rt △EMF 中,由勾股定理求出即可.【详解】(1)∵现将纸片折叠,使点D 与点B 重合,折痕为EF ,∴∠DEF =∠BEF .∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠DEF =∠BFE ,∴∠BEF =∠BFE ,∴BE =BF ,即△BEF 是等腰三角形;(2)过E 作EM ⊥BC 于M ,则四边形ABME 是矩形,所以EM =AB =6,AE =BM .∵现将纸片折叠,使点D与点B重合,折痕为EF,∴DE=BE,DO=BO,BD⊥EF.∵四边形ABCD是矩形,BC=8,∴AD=BC=8,∠BAD=90°.在Rt△ABE中,AE2+AB2=BE2,即(8﹣BE)2+62=BE2,解得:BE==DE=BF,AE=8﹣DE=8﹣==BM,∴FM=﹣=.在Rt△EMF中,由勾股定理得:EF==.故答案为:.【点睛】本题考查了折叠的性质和矩形性质、勾股定理等知识点,能熟记折叠的性质是解答此题的关键.11.如图,抛物线y=mx2+2mx+n经过A(﹣3,0),C(0,﹣32)两点,与x轴交于另一点B.(1)求经过A,B,C三点的抛物线的解析式;(2)过点C作CE∥x轴交抛物线于点E,写出点E的坐标,并求AC、BE的交点F的坐标(3)若抛物线的顶点为D,连结DC、DE,四边形CDEF是否为菱形?若是,请证明;若不是,请说明理由.【答案】(1)y=12x2+x﹣32;(2)F点坐标为(﹣1,﹣1);(3)四边形CDEF是菱形.证明见解析【解析】【分析】将A、C点的坐标代入抛物线的解析式中,通过联立方程组求得该抛物线的解析式;根据(1)题所得的抛物线的解析式,可确定抛物线的对称轴方程以及B、C点的坐标,由CE∥x轴,可知C、E关于对称轴对称。
专题07 特殊的平行四边形中折叠问题(解析版)八年级数学下册期末综合复习专题提优训练(人教版)

2020-2021学年八年级数学下册期末综合复习专题提优训练(人教版)专题07 特殊的平行四边形中折叠问题【典型例题】1.如图所示,长方形纸片ABCD 的长AD =8cm ,宽AB =4cm ,将其折叠,使点D 与点B 重合. (1)求证:BE =BF ;(2)求折叠后DE 的长;(2)求以折痕EF 为边的正方形面积.【答案】(1)证明见解析;(2)5cm ;(3)20cm 2.【详解】(1)在长方形ABCD 中,AD //BC ,DEF EFB ∴∠=∠,DEF BEF ∠=∠,EFB BEF ∴∠=∠,∴ BE =BF ,设DE =x cm ,则BE =x cm ,AE =()8x cm -,在Rt ABE △中,由勾股定理()22248x x +-=, ∴5x =,即DE 的长为5cm .(2)过E 作EH BF ⊥于点H ,则EH =AB =4,BH =AE =3,∴ HF =BF -BH =5-3=2,∴2222420EF =+=,∴ 以EF 为边长的正方形的面积为220cm .【专题训练】一、选择题1.如图,将菱形纸片ABCD 折叠,使点A 恰好落在菱形的对称中心O 处,折痕为EF .若菱形ABCD 的边长为4,120B ∠=︒,则EF 的值是( )A B .2 C .D .4【答案】B【分析】 根据菱形的性质证明∴ABD 是等边三角形,求得BD =4,再证明EF 是∴ABD 的中位线即可得到结论.【详解】解:连接AC ,BD∴四边形ABCD 是菱形,∴AC BD ⊥,BD 平分∴ABC ,4AB BC CD DA ==== ∴∴111206022ABD ABC ︒=∠=⨯=︒ ∴AB AD =∴∴ABD 是等边三角形,∴ 4.BD =由折叠的性质得:EF AO ⊥,EF 平分AO ,又∴BD AC ⊥,∴//EF BD∴EF 为∴ABD 的中位线, ∴122EF BD == 故选:B .【点睛】本题考查了折叠性质,菱形性质,主要考查学生综合运用定理进行推理和计算的能力.2.如图,把正方形纸片ABCD 沿对边中点所在的直线对折后展开,折痕为MN ,再过点C 折叠纸片,使点C 落在MN 上的点F 处,折痕为BE .若AB 的长为1,则FM 的长为( )A .1B .2C .2D .12【答案】B【分析】根据翻折得到1FB BC ==,12BM =,在Rt BFM 中,可利用勾股定理求出FM 的值. 【详解】 解:四边形ABCD 是正方形, 1AB BC ∴==,由折叠的性质可知,1FB BC ==,1122BM AB ==, 在Rt BFM 中,由勾股定理得:2FM ===. 故选:B .【点睛】本题考查翻折、正方形的性质、勾股定理等知识,是重要考点,难度较易,掌握相关知识是解题关键. 3.将矩形纸片ABCD 按如图所示的方式折叠,得到菱形AECF .若AB =3,则BC 的长为( )A .1B .2CD 【答案】D【分析】 根据菱形及矩形的性质可得到∴BAC 的度数,从而根据直角三角形的性质求得BC 的长.【详解】解:∴四边形AECF 为菱形,∴∴FCO =∴ECO ,EC =AE ,由折叠的性质可知,∴ECO =∴BCE ,又∴FCO +∴ECO +∴BCE =90°,∴∴FCO =∴ECO =∴BCE =30°,在Rt ∴EBC 中,EC =2EB ,又∴EC =AE ,AB =AE +EB =3,∴EB=1,EC=2,∴Rt∴BCE中,BC ,故选:D.【点睛】本题主要考查了菱形的性质以及矩形的性质,解决问题的关键是根据折叠以及菱形的性质发现特殊角,根据30°的直角三角形中各边之间的关系求得BC的长.4.如图,在正方形ABCD中,AB=6,点E,F分别在边AB,CD上,∴EFC=120°.若将四边形EBCF沿EF 折叠,点B恰好落在AD边上,则AE的长度为()A.2B C D.1【答案】A【分析】依据正方形的性质以及折叠的性质,即可得到∴AEB'=60°,再根据含30°角的直角三角形的性质,即可得到AE的长.【详解】解:∴四边形ABCD是正方形,∴AB∴CD,∴A=90°,∴∴BEF=180°-∴EFC=60°,∴将四边形EBCF沿EF折叠,点B恰好落在AD边上,∴∴BEF=∴FEB'=60°,BE=B'E,∴∴AEB'=180°-∴BEF-∴FEB'=60°,∴∴AB'E=30°,∴B'E=2AE,设AE=x,则B'E=2x=BE,∴AB=6,∴x+2x=6,解得x=2.故选:A.【点睛】本题考查了正方形的性质,折叠的性质,含30°角的直角三角形的性质等知识点,能综合性运用性质进行推理是解此题的关键.5.如图,菱形ABCD中,∴ABC=60°,AB=4,E是边AD上一动点,将∴CDE沿CE折叠,得到∴CFE,则∴BCF 面积的最大值是()A.8B.C.16D.【答案】A【分析】由三角形底边BC是定长,所以当∴BCF的高最大时,∴BCF的面积最大,即当FC∴BC时,三角形有最大面积.【详解】解:在菱形ABCD中,BC=CD=AB=4又∴将∴CDE沿CE折叠,得到∴CFE,∴FC=CD=4由此,∴BCF的底边BC是定长,所以当∴BCF的高最大时,∴BCF的面积最大,即当FC∴BC时,三角形有最大面积∴∴BCF面积的最大值是11448 22BC FC=⨯⨯=故选:A.【点睛】本题考查菱形的性质和折叠的性质,掌握三角形面积的计算方法和菱形的性质正确推理计算是解题关键. 6.如图,有一张矩形纸条ABCD ,AB =5cm ,BC =2cm ,点M ,N 分别在边AB ,CD 上,CN =1cm .现将四边形BCNM 沿MN 折叠,使点B ,C 分别落在点B ′,C ′上.在点M 从点A 运动到点B 的过程中,若边MB '与边CD 交于点E ,则点E 相应运动的路径长为( )cm .A 32B .52CD .32【答案】A【分析】探究点E 的运动轨迹,寻找特殊位置解决问题即可.【详解】解:如图1中,∴四边形ABCD 是矩形,∴AB ∴CD ,∴∴1=∴3,由翻折的性质可知:∴1=∴2,BM =MB ′,∴∴2=∴3,∴MB ′=NB ′,∴NB '==cm ),∴BM NB '==(cm ).如图2中,当点M 与A 重合时,同理可得:AE =EN ,设AE =EN =x cm ,在Rt ∴ADE 中,则有2222(4)=+-x x ,解得x =52, ∴53422DE =-=(cm ), 如图3中,当点M 运动到MB ′∴AB 时,DE ′的值最大,DE ′=5-1-2=2(cm ),如图4中,当点M 运动到点B ′落在CD 时,DB ′(即DE ″)51(4=-=(cm ),∴点E 的运动轨迹E →E ′→E ″,运动路径3322(4)22EE E B '''=+=-+-=(cm ). 故选:A .【点睛】本题考查了翻折变换,矩形的性质,勾股定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考填空题中的压轴题.二、填空题7.如图a 是长方形纸带,∴DEF =22°,将纸带沿EF 折叠成图b ,再沿BF 折叠成图c ,则图c 中的∴CFE 的度数是________°.【答案】114°【分析】根据两直线平行,内错角相等可得∴EFB=∴DEF,再根据翻折的性质,图c中∴EFB处重叠3层,然后根据∴CFE=180°-3∴EFB代入数据行计算即可得解【详解】∴∴DEF =22°长方形ABCD的对边AD//BC∴∴EFB=∴DEF=22°由折叠,∴EFB处折叠了3层∴∴CFE=180° -3∴EFB=180°—3 × 22°=114°故答案为:114°【点睛】本题考查折叠问题,熟知折叠中蕴含着全等,有相等的角与边进行分析是关键.8.如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC 边上的点F处,则CE=_____.【答案】4 3【分析】由折叠求出BF和CF,再设CF=x,在∴CEF中用勾股定理列方程即可得答案.【详解】解:∴矩形ABCD沿AE折叠,AB=3,AD=5,∴AF=AD=5,∴B=∴C=90°,DE=EF,∴BF4,∴CF=BC﹣BF=1,设CE=x,则EF=DE=3﹣x,在Rt∴CEF中,CE2+CF2=EF2,∴x2+12=(3﹣x)2,解得x=43,∴CE=43.故答案为:43.【点睛】本题考查矩形性质及勾股定理应用等知识,解题的关键是在Rt∴CEF中用勾股定理列方程.9.如图,将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,折痕为MN,若32NEC FMN∠=︒∠=,_____︒.【答案】119【分析】根据正方形的性质得到∴A=∴C=∴D=90°,根据折叠的性质得到∴F=∴A=90°,∴FEN=∴C=90°,∴DNM=∴ENM,根据平角的定义得到∴ENM=12(180°-∴ENC)=12(180°-58°)=61°,根据四边形的内角和即可得到结论.【详解】解:∴四边形ABCD是正方形,∴∴A=∴C=∴D=90°,∴将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,∴∴F=∴A=90°,∴FEN=∴D=90°,∴DNM=∴ENM,∴∴NEC=32°,∴∴ENC=58°,∴∴ENM=12(180°-∴ENC)=12(180°-58°)=61°,∴∴FMN =360°-90°-90°-61°=119°,故答案为:119.【点睛】本题考查了角的计算,翻折变换的问题,折叠问题其实质是轴对称,对应线段相等,对应角相等,找到相等的角是解决本题的关键.10.对角线长分别为6和8的菱形ABCD 如图所示,点O 为对角线的交点,过点O 折叠菱形,使B ,B '两点重合,MN 是折痕.若1B M '=,则CN 的长为_______.【答案】4【分析】连接AC 、BD ,如图,利用菱形的性质得132OC AC ==,142OD BD ==,90COD ∠=︒,再利用勾股定理计算出5CD =,接着证明OBM ODN ∆≅∆得到DN BM =,然后根据折叠的性质得1BM BM'==,从而有1DN =,于是计算CD DN -即可.【详解】解:连接AC 、BD ,如图,点O 为菱形ABCD 的对角线的交点,132OC AC ∴==,142OD BD ==,90COD ∠=︒, 在Rt COD ∆中,5CD ==,//AB CD ,MBO NDO ∴∠=∠,在OBM ∆和ODN ∆中MBO NDO OB ODBOM DON ∠=∠⎧⎪=⎨⎪∠=∠⎩, OBM ODN ∴∆≅∆,DN BM ∴=,过点O 折叠菱形,使B ,B ′两点重合,MN 是折痕,1BM BM'∴==, 1DN ∴=,514CN CD DN ∴=-=-=,故答案为:4.【点睛】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了菱形的性质.11.如图,矩形ABCD 中,6,8AB BC ==,点E 是BC 边上一点,连接AE ,把ABE △沿AE 折叠,使点B 落在点F 处,当CEF △为直角三角形时,CF 的长为________.【答案】4或【分析】当CEF △为直角三角形时,有两种情况:①当点F 落在矩形内部时,如答图1所示.连接AC ,先利用勾股定理计算出10AC =,根据折叠的性质得90AFE B ∠=∠=︒,而当CEF △为直角三角形时,只能得到90EFC ∠=︒,所以点A 、F 、C 共线,即B 沿AE 折叠,使点B 落在对角线AC 上的点F 处,则,6EB EF AB AF ===,可计算出CF ; ②当点F 落在AD 边上时,如答图2所示.此时ABEF 为正方形,根据勾股定理计算出CF .【详解】解:当CEF △为直角三角形时,有两种情况:①当点F 落在矩形内部时,如答图1所示.连接AC ,在Rt ABC 中,6,8AB BC ==,∴10AC =,∴B 沿AE 折叠,使点B 落在点F 处,∴90AFE B ∠=∠=︒,当CEF △为直角三角形时,只能得到90EFC ∠=︒,∴点A 、F 、C 共线,即B 沿AE 折叠,使点B 落在对角线AC 上的点F 处,∴,6EB EF AB AF ===,∴1064CF =-=;②当点F 落在AD 边上时,如答图2所示.此时ABEF 为正方形,∴6,862BE AB CE ===-=,∴CF =综上所述,CF 的长为4或.故答案为:4或.【点睛】本题考查折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了矩形的性质以及勾股定理.解题的关键是要注意本题有两种情况,需要分类讨论,避免漏解.12.如图,在正方形ABCD 中,12AB =,点E 在边CD 上,3CD DE =.将ADE 沿AE 对折至AFE △,延长EF 交边BC 于点G ,连接AG ,CF .有下列结论:①ABG AFG ≅;②BG GC =;③//AG CF ;④6FGC S =△.其中正确的结论是__________.(填序号)【答案】①②③【分析】由正方形的性质和折叠的性质得出AB =AF ,∴AFG =90°,由HL 证明Rt ∴ABG ∴Rt ∴AFG ,得出①正确;设BG =FG =x ,则CG =12-x .由勾股定理得出方程,解方程求出BG ,得出GC ,即可得出②正确;由全等三角形的性质和三角形内角和定理得出∴AGB =∴AGF =∴GFC =∴GCF ,得出AG ∴CF ,即可得出③正确;通过计算三角形的面积得出④错误;即可得出结果.【详解】解:①正确.理由如下:四边形ABCD 是正方形,12AB BC CD AD ∴====,90B GCE D ∠=∠=∠=︒,由折叠的性质得:AF AD =,90AFE D ∠=∠=︒,90AFG ∴∠=︒,AB AF =,在Rt ABG △和Rt AFG △中,AG AG AB AF=⎧⎨=⎩, Rt Rt (HL)ABG AFG ∴≅△△;②正确.理由如下: 由题意得:143EF DE CD ===,设BG FG x ==,则12CG x =-. 在直角ECG 中,根据勾股定理,得222(12)8(4)x x -+=+,解得:6x =,6BG ∴=,1266GC ∴=-=,BG GC ∴=;③正确.理由如下:CG BG =,BG GF =,CG GF ∴=,FGC ∴△是等腰三角形,GFC GCF ∠=∠.又∴Rt Rt ABG AFG ≅△△,AGB AGF ∴∠=∠,218022+==︒-=+==∠∠∠∠∠∠∠∠AGB AGF AGB FGC GFC GCF GFC GCF ,AGB AGF GFC GCF ∴∠=∠=∠=∠,//AG CF ∴;④错误;理由如下:11682422GCE S GC CE =⋅=⨯⨯=△, 6GF =,4EF =,GFC 和FCE △等高,:3:2GFC FCE S S ∴=△△,37224655GFC S ∴=⨯=≠△. 故④不正确.∴正确的个数有①②③.故答案为:①②③.【点睛】本题考查的是翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理,平行线的判定,三角形的面积计算等知识;本题综合性强,有一定的难度.三、解答题13.如图,矩形纸片 ABCD 的长 AD =10cm ,宽 AB =5cm ,将其折叠,使点 D 与点 B 重合,那么折叠后AE 的长是多少?【答案】154cm【分析】设DE =x ,根据折叠的性质可得BE =x ,表示出AE =10−x ,然后在Rt ∴ABE 中,利用勾股定理列式计算即可得解.【详解】解:设 DE =xcm ,则BE =xcm ,∴AE =(10﹣x )cm ,∴在 Rt ∴ABE 中,AB 2+AE 2=BE 2,∴52+(10﹣x )2=x 2,∴解得:x =254, ∴AE =10﹣254=154cm 答:折叠后AE 的长是154cm . 【点睛】本题考查了矩形的性质,折叠的性质,勾股定理的应用,根据勾股定理列出方程是解题的关键. 14.如图,在菱形ABCD 中,120ABC ∠=︒,将菱形折叠,使点A 恰好落在对角线BD 上的点G 处(不与B D ,重合),折痕为EF ,若26DG BG ==,,求AF 的长.【答案】AF 的长为267. 【分析】 作FH BD ⊥于点H ,通过菱形的性质和折叠的性质证明ABD △为等边三角形,设AF x =,则FG x =,8DF x =-,在Rt DFH 中,利用特殊角表示出DH ,FH ,最后在Rt FHG 中利用勾股定理即可求解.【详解】如图,作FH BD ⊥于点H .由折叠的性质可知,FG FA =.由题意,得8BD DG BG =+=.∴ 四边形ABCD 是菱形. ∴1602AD AB ABD CBD ABC =∠=∠=∠=︒,, ∴ABD △为等边三角形,∴8AD BD ==.设AF x =,则FG x =,8DF x =-,在Rt DFH 中,∴60FDH ∠=︒,∴()118422DH x x =-=-,)822FH x x =-=, ∴1222HG DH x =-=-. 在Rt FHG 中,222FG FH GH =+,即222122x x x ⎛⎫⎛⎫=+- ⎪ ⎪ ⎪⎝⎭⎝⎭, 解得267x =, ∴AF 的长为267. 【点睛】本题主要考查菱形的性质,含30°的直角三角形的性质,折叠的性质,勾股定理,掌握菱形的性质,勾股定理及方程的思想是解题的关键.15.如图,正方形纸片ABCD 的边长为6,点E 、F 分别在边BC 、CD 上,将AB 、AD 分别沿AE 、AF 折叠,点B 、D 恰好都在点G 处,已知2BE =,求FC 的长.【答案】3【分析】因为正方形ABCD 的边长为6,由图形折叠可得=2BE EG =,624EC =-=,6DF FG x ==-, 再利用勾股定理进行计算即可.【详解】解:设FC x =,由图形折叠可得=2BE EG =,624EC =-=,6DF FG x ==-,在直角ECF ∆中,∴222EF EC CF =+,∴222(426)x x +-=+,解得3x =,∴3=FC .【点睛】此题考查了折叠问题,解题的关键是找准不变的线段,利用勾股定理求解线段.16.如图,AC 为矩形ABCD 的对角线,将边AB 沿AE 折叠,使点B 落在AC 上的点M 处,将边CD 沿CF 折叠,使点D 落在AC 上的点N 处.(1)求证:四边形AECF 是平行四边形;(2)若AB =6,AC =10,求四边形AECF 的面积.【答案】(1)证明见解析;(2)30.【解析】试题分析:(1)首先由矩形的性质和折叠的性质证得AB =CD ,AD ∴BC ,∴ANF =90°,∴CME =90°,易得AN =CM ,可得∴ANF∴∴CME(ASA),由平行四边形的判定定理可得结论;(2)由AB=6,AC=10,可得BC=8,设CE=x,则EM=8-x,CM=10-6=4,在Rt∴CEM中,利用勾股定理可解得x,由平行四边形的面积公式可得结果.试题解析:(1)证明:∴折叠,∴AM=AB,CN=CD,∴FNC=∴D=90°,∴AME=∴B=90°,∴∴ANF=90°,∴CME=90°,∴四边形ABCD为矩形,∴AB=CD,AD∴BC,∴AM=CN,∴AM﹣MN=CN﹣MN,即AN=CM,在∴ANF和∴CME中,{FAN EMC AN CMANF CME∠=∠=∠=∠,∴∴ANF∴∴CME(ASA),∴AF=CE,又∴AF∴CE,∴四边形AECF是平行四边形;(2)解:∴AB=6,AC=10,∴BC=8,设CE=x,则EM=8﹣x,CM=10﹣6=4,在Rt∴CEM中,(8﹣x)2+42=x2,解得:x=5,∴四边形AECF的面积的面积为:EC•AB=5×6=30.17.如图1.将矩形ABCD沿DE折叠使点A落在A'处,然后将矩形展平,沿EF折叠使点A落在折痕DE 上的点G处,再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处,如图2.(1)求证:EG=CH;(2)已知AF∴CDE的面积.【答案】(1)见解析;(2)∴CDE的面积=4+【分析】(1)由折叠的性质及矩形的性质可得AD AE BC ==,AE EG =,BC CH =,可得结论;(2)由折叠的性质可知45ADE ∠=︒,90FGE A ∠=∠=︒,AF =,那么DG =,利用勾股定理求出2DF =,于是可得2AD AF DF =+=;再利用AAS 证明AEF BCE △≌△,得到AF BE =,于是22AB AE BE =+=+=,即可求解.【详解】(1)证明:四边形ABCD 是矩形, AD BC ∴=,将矩形ABCD 沿DE 折叠使点A 落在A '处,AD A D '∴=,AE A E '=,45ADE A DE '∠=∠=︒,45ADE AED ∴∠=∠=︒,AD AE ∴=,AE BC ∴=,由折叠的性质可得AE EG =,BC CH =,EG CH ∴=;(2)45ADE ∠=︒,90FGE A ∠=∠=︒,AFDG ∴=2DF =,2AD AF DF ∴=+;由折叠知AEF GEF ∠=∠,BEC HEC ∠=∠,90GEF HEC ∴∠+∠=︒,90AEF BEC ∠+∠=︒,90∠+∠=︒AEF AFE ,BEC AFE ∴∠=∠,在AEF 与BCE 中,90AFE BEC A B AE BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩, ()AEF BCE AAS ∴△≌△,AF BE∴=,22AB AE BE CD ∴=+=+==,CDE ∴的面积11(2(24 22CD AD=⨯⨯=⨯+⨯=+【点睛】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了全等三角形的判定与性质,矩形的性质,勾股定理等知识.18.如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF 折叠,使点D落在AC上的点N处.(1)求证:四边形AECF是平行四边形;(2)当∴BAE为多少度时,四边形AECF是菱形?请说明理由.【答案】(1)证明见解析(2)当∴BAE=30°时,四边形AECF是菱形【分析】(1)首先证明∴ABE∴∴CDF,则DF=BE,然后可得到AF=EC,依据一组对边平行且相等四边形是平行四边形可证明AECF是平行四边形;(2)由折叠性质得到∴BAE=∴CAE=30°,求得∴ACE=90°-30°=60°,即∴CAE=∴ACE,得到EA=EC,于是得到结论.【详解】(1)∴四边形ABCD为矩形,∴AB=CD,AD∴BC,∴B=∴D=90°,∴BAC=∴DCA.由翻折的性质可知:∴EAB=12∴BAC,∴DCF=12∴DCA.∴∴EAB=∴DCF.在∴ABE和∴CDF中B DAB CDEAB DCF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴∴ABE∴∴CDF(ASA),∴DF=BE.∴AF=EC.又∴AF∴EC,∴四边形AECF是平行四边形;(2)当∴BAE=30°时,四边形AECF是菱形,理由:由折叠可知,∴BAE=∴CAE=30°,∴∴B=90°,∴∴ACE=90°-30°=60°,即∴CAE=∴ACE,∴EA=EC,∴四边形AECF是平行四边形,∴四边形AECF是菱形.【点睛】本题主要考查了菱形的判定,全等三角形的判定和性质,折叠的性质、矩形的性质、平行四边形的判定定理和勾股定理等,综合运用各定理是解答此题的关键.19.探究:如图①点E、F分别在正方形ABCD的边BC、CD上,连结AE、AF、EF,将∴ABE、∴ADF分别沿AE、AF折叠,折叠后的图形恰好能拼成与∴AEF完全重合的三角形.若BE=2,DF=3,求AB的长;拓展:如图②点E、F分别在四边形BACD的边BC、CD上,且∴B=∴D=90°.连结AE、AF、EF将∴ABE、∴ADF分别沿AE、AF折叠,折叠后的图形恰好能拼成与∴AEF完全重合的三角形.若∴EAF=30°,AB=4,则∴ECF的周长是.【答案】探究:AB=6;拓展:.3【分析】探究:设:正方形的边长为a,则EC=a-2,CF=a-3,则由勾股定理得:EF2=EC2+CF2,即可求解;拓展:证明∴ABC∴∴ADC,∴BAE+∴DAF=∴EAF=30°,则∴BAD=60°,∴BAC=∴DAC=12(∴BAD)=30°,CD=BC=ABtan∴BAC,即可求解.【详解】探究:设:正方形的边长为a,则EC=a﹣2,CF=a﹣3,则EF=BE+DF=5,则EF2=EC2+CF2,即:25=(a﹣2)2+(a﹣3)2,解得:a=6或﹣1(舍去﹣1),故AB=6;拓展:由题意得:AB=CD=4,连接AC,∴AB=CD,AC=AC,∴∴ABC∴∴ADC,∴BC=CD,∴BAC=∴DAC,∴点E、F分别在四边形BACD的边BC、CD上,故:∴BAE+∴DAF=∴EAF=30°,则∴BAD=60°,∴∴BAC=∴DAC=12(∴BAD)=30°,CD=BC=ABtan∴BAC=4∴ECF的周长=EF+EC+FC=AE+FD+EC+FC=AC+CD=2CD,故答案为:3. 【点睛】 本题考查的是翻折变换(折叠问题),涉及到正方形的性质、三角形全等等,其中(2)证明∴ABC ∴∴ADC ,是本题解题的关键.20.(1)如图1,将矩形ABCD 折叠,使AB 落在对角线AC 上,折痕为AE ,点B 落在点1B 处,若66DAC ∠=︒,则BAE ∠= º;(2)小丽手中有一张矩形纸片,9AB =,4=AD .她准备按如下两种方式进行折叠:①如图2,点F 在这张矩形纸片的边CD 上,将纸片折叠,使点D 落在边AB 上的点1D 处,折痕为FG ,若5DF =,求AG 的长;②如图3,点H 在这张矩形纸片的边AB 上,将纸片折叠,使HA 落在射线HC 上,折痕为HK ,点A ,D 分别落在1A ,2D 处,若73DK =,求1AC 的长. 【答案】(1)12;(2)①AG =32;②13A C = 【分析】 (1)由折叠的性质可得∴BAE =∴CAE =12°;(2)①过点F 作FH ∴AB 于H ,可证四边形DFHA 是矩形,可得AD =FH =4,由勾股定理可求D 1H =3,由勾股定理可求AG 的长;②首先证明CK =CH ,利用勾股定理求出BH ,可得AH ,再利用翻折不变性,可知AH =A 1H ,由此即可解决问题.【详解】解:(1)∴∴DAC =66°,∴∴CAB =24°∴将矩形ABCD 折叠,使AB 落在对角线AC 上,∴∴BAE=∴CAE=12°故答案为:12;(2)如图2,过点F作FH∴AB于H,∴∴D=∴A=90°,FH∴AB∴四边形DFHA是矩形∴AD=FH=4,∴将纸片ABCD折叠∴DF=D1F=5,DG=D1G,∴D 1H2225163FH,∴AD1=2∴AG2+D1A2=D1G2,∴AG2+4=(4−AG)2,∴AG=32;②∴DK=73,CD=9,∴CK=9−73=203,∴四边形ABCD是矩形,∴DC∴AB,∴∴CKH=∴AHK,由翻折不变性可知,∴AHK=∴CHK,∴∴CKH=∴CHK,∴CK=CH=203,∴CB=AD=4,∴B=90°,∴在Rt∴CDF中,BH22400161693BC,∴AH=AB−BH=11 3,由翻折不变性可知,AH=A1H=11 3,∴A1C=CH−A1H=3.【点睛】本题考查四边形综合题、矩形的性质、翻折变换、勾股定理,解题的关键是灵活运用所学知识解决问题,学会利用翻折不变性解决问题,属于中考压轴题.。
八年级平行四边形压轴题

八年级平行四边形压轴题一、选择题(每题3分,共15分)1. 在平行四边形ABCD中,对角线AC与BD相交于点O,若AC = 8,BD = 10,AB = 6,则△OAB的周长为()- A. 12.- B. 15.- C. 20.- D. 16.- 解析:- 因为平行四边形对角线互相平分,所以OA = 1/2AC = 4,OB = 1/2BD = 5。
- 又已知AB = 6,所以△OAB的周长为OA+OB + AB=4 + 5+6 = 15。
答案为B。
2. 平行四边形ABCD中,∠A:∠B = 2:1,则∠C的度数为()- A. 60°.- B. 120°.- C. 45°.- D. 30°.- 解析:- 因为平行四边形邻角互补,即∠A+∠B = 180°,又∠A:∠B = 2:1,设∠B=x,则∠A = 2x,所以2x+x=180°,解得x = 60°。
- ∠A = 120°,平行四边形对角相等,所以∠C=∠A = 120°。
答案为B。
3. 下列条件中,不能判定四边形ABCD是平行四边形的是()- A. AB = CD,AD = BC.- B. AB∥CD,AB = CD.- C. AB = CD,AD∥BC.- D. AB∥CD,AD∥BC.- 解析:- 根据平行四边形的判定定理,A选项两组对边分别相等可判定是平行四边形;B 选项一组对边平行且相等可判定是平行四边形;D选项两组对边分别平行可判定是平行四边形。
- C选项一组对边相等,另一组对边平行,不能判定是平行四边形,答案为C。
4. 平行四边形ABCD的周长为36cm,AB = 8cm,则BC的长为()- A. 10cm.- B. 16cm.- C. 14cm.- D. 28cm.- 解析:- 平行四边形的周长等于两组对边之和,即2(AB + BC)=36,已知AB = 8cm,代入可得2(8 + BC)=36,16+2BC = 36,2BC = 20,BC = 10cm。
备战中考数学—平行四边形的综合压轴题专题复习含答案

备战中考数学—平行四边形的综合压轴题专题复习含答案一、平行四边形1.四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.(1)如图1,当点E、F在线段AD上时,①求证:∠DAG=∠DCG;②猜想AG与BE的位置关系,并加以证明;(2)如图2,在(1)条件下,连接HO,试说明HO平分∠BHG;(3)当点E、F运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出∠BHO的度数.【答案】(1)①证明见解析;②AG⊥BE.理由见解析;(2)证明见解析;(3)∠BHO=45°.【解析】试题分析:(1)①根据正方形的性质得DA=DC,∠ADB=∠CDB=45°,则可根据“SAS”证明△ADG≌△CDG,所以∠DAG=∠DCG;②根据正方形的性质得AB=DC,∠BAD=∠CDA=90°,根据“SAS”证明△ABE≌△DCF,则∠ABE=∠DCF,由于∠DAG=∠DCG,所以∠DAG=∠ABE,然后利用∠DAG+∠BAG=90°得到∠ABE+∠BAG=90°,于是可判断AG⊥BE;(2)如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,证明△AON≌△BOM,可得四边形OMHN为正方形,因此HO平分∠BHG结论成立;(3)如答图2所示,与(1)同理,可以证明AG⊥BE;过点O作OM⊥BE于点M,ON⊥AG于点N,构造全等三角形△AON≌△BOM,从而证明OMHN为正方形,所以HO 平分∠BHG,即∠BHO=45°.试题解析:(1)①∵四边形ABCD为正方形,∴DA=DC,∠ADB=∠CDB=45°,在△ADG和△CDG中,∴△ADG≌△CDG(SAS),∴∠DAG=∠DCG;②AG⊥BE.理由如下:∵四边形ABCD为正方形,∴AB=DC,∠BAD=∠CDA=90°,在△ABE和△DCF中,∴△ABE≌△DCF(SAS),∴∠ABE=∠DCF,∵∠DAG=∠DCG,∴∠DAG=∠ABE,∵∠DAG+∠BAG=90°,∴∠ABE+∠BAG=90°,∴∠AHB=90°,∴AG⊥BE;(2)由(1)可知AG⊥BE.如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,则四边形OMHN为矩形.∴∠MON=90°,又∵OA⊥OB,∴∠AON=∠BOM.∵∠AON+∠OAN=90°,∠BOM+∠OBM=90°,∴∠OAN=∠OBM.在△AON与△BOM中,∴△AON≌△BOM(AAS).∴OM=ON,∴矩形OMHN为正方形,∴HO平分∠BHG.(3)将图形补充完整,如答图2示,∠BHO=45°.与(1)同理,可以证明AG⊥BE.过点O作OM⊥BE于点M,ON⊥AG于点N,与(2)同理,可以证明△AON≌△BOM,可得OMHN为正方形,所以HO平分∠BHG,∴∠BHO=45°.考点:1、四边形综合题;2、全等三角形的判定与性质;3、正方形的性质2.如图,平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M 沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了x秒.(1)P点的坐标为多少(用含x的代数式表示);(2)试求△NPC面积S的表达式,并求出面积S的最大值及相应的x值;(3)当x为何值时,△NPC是一个等腰三角形?简要说明理由.【答案】(1)P点坐标为(x,3﹣x).(2)S的最大值为,此时x=2.(3)x=,或x=,或x=.【解析】试题分析:(1)求P点的坐标,也就是求OM和PM的长,已知了OM的长为x,关键是求出PM的长,方法不唯一,①可通过PM∥OC得出的对应成比例线段来求;②也可延长MP交BC于Q,先在直角三角形CPQ中根据CQ的长和∠ACB的正切值求出PQ的长,然后根据PM=AB﹣PQ来求出PM的长.得出OM和PM的长,即可求出P点的坐标.(2)可按(1)②中的方法经求出PQ的长,而CN的长可根据CN=BC﹣BN来求得,因此根据三角形的面积计算公式即可得出S,x的函数关系式.(3)本题要分类讨论:①当CP=CN时,可在直角三角形CPQ中,用CQ的长即x和∠ABC的余弦值求出CP的表达式,然后联立CN的表达式即可求出x的值;②当CP=PN时,那么CQ=QN,先在直角三角形CPQ中求出CQ的长,然后根据QN=CN﹣CQ求出QN的表达式,根据题设的等量条件即可得出x的值.③当CN=PN时,先求出QP和QN的长,然后在直角三角形PNQ中,用勾股定理求出PN 的长,联立CN的表达式即可求出x的值.试题解析:(1)过点P作PQ⊥BC于点Q,有题意可得:PQ∥AB,∴△CQP∽△CBA,∴∴解得:QP=x,∴PM=3﹣x,由题意可知,C(0,3),M(x,0),N(4﹣x,3),P点坐标为(x,3﹣x).(2)设△NPC的面积为S,在△NPC中,NC=4﹣x,NC边上的高为,其中,0≤x≤4.∴S=(4﹣x)×x=(﹣x2+4x)=﹣(x﹣2)2+.∴S的最大值为,此时x=2.(3)延长MP交CB于Q,则有PQ⊥BC.①若NP=CP,∵PQ⊥BC,∴NQ=CQ=x.∴3x=4,∴x=.②若CP=CN,则CN=4﹣x,PQ=x,CP=x,4﹣x=x,∴x=;③若CN=NP,则CN=4﹣x.∵PQ=x,NQ=4﹣2x,∵在Rt△PNQ中,PN2=NQ2+PQ2,∴(4﹣x)2=(4﹣2x)2+(x)2,∴x=.综上所述,x=,或x=,或x=.考点:二次函数综合题.3.操作与证明:如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.(1)连接AE,求证:△AEF是等腰三角形;猜想与发现:(2)在(1)的条件下,请判断MD、MN的数量关系和位置关系,得出结论.结论1:DM、MN的数量关系是;结论2:DM、MN的位置关系是;拓展与探究:(3)如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,则(2)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.【答案】(1)证明参见解析;(2)相等,垂直;(3)成立,理由参见解析.【解析】试题分析:(1)根据正方形的性质以及等腰直角三角形的知识证明出CE=CF,继而证明出△ABE≌△ADF,得到AE=AF,从而证明出△AEF是等腰三角形;(2)DM、MN的数量关系是相等,利用直角三角形斜边中线等于斜边一半和三角形中位线定理即可得出结论.位置关系是垂直,利用三角形外角性质和等腰三角形两个底角相等性质,及全等三角形对应角相等即可得出结论;(3)成立,连接AE,交MD于点G,标记出各个角,首先证明出MN∥AE,MN=AE,利用三角形全等证出AE=AF,而DM=AF,从而得到DM,MN数量相等的结论,再利用三角形外角性质和三角形全等,等腰三角形性质以及角角之间的数量关系得到∠DMN=∠DGE=90°.从而得到DM、MN的位置关系是垂直.试题解析:(1)∵四边形ABCD是正方形,∴AB=AD=BC=CD,∠B=∠ADF=90°,∵△CEF是等腰直角三角形,∠C=90°,∴CE=CF,∴BC﹣CE=CD﹣CF,即BE=DF,∴△ABE≌△ADF,∴AE=AF,∴△AEF是等腰三角形;(2)DM、MN的数量关系是相等,DM、MN的位置关系是垂直;∵在Rt△ADF中DM是斜边AF的中线,∴AF=2DM,∵MN 是△AEF的中位线,∴AE=2MN,∵AE=AF,∴DM=MN;∵∠DMF=∠DAF+∠ADM,AM=MD,∵∠FMN=∠FAE,∠DAF=∠BAE,∴∠ADM=∠DAF=∠BAE,∴∠DMN=∠FMN+∠DMF=∠DAF+∠BAE+∠FAE=∠BAD=90°,∴DM⊥MN;(3)(2)中的两个结论还成立,连接AE,交MD于点G,∵点M为AF的中点,点N为EF的中点,∴MN∥AE,MN=AE,由已知得,AB=AD=BC=CD,∠B=∠ADF,CE=CF,又∵BC+CE=CD+CF,即BE=DF,∴△ABE≌△ADF,∴AE=AF,在Rt△ADF中,∵点M为AF的中点,∴DM=AF,∴DM=MN,∵△ABE≌△ADF,∴∠1=∠2,∵AB∥DF,∴∠1=∠3,同理可证:∠2=∠4,∴∠3=∠4,∵DM=AM,∴∠MAD=∠5,∴∠DGE=∠5+∠4=∠MAD+∠3=90°,∵MN∥AE,∴∠DMN=∠DGE=90°,∴DM⊥MN.所以(2)中的两个结论还成立.考点:1.正方形的性质;2.全等三角形的判定与性质;3.三角形中位线定理;4.旋转的性质.4.在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(5,0),点B(0,3).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.(1)如图①,当点D落在BC边上时,求点D的坐标;(2)如图②,当点D落在线段BE上时,AD与BC交于点H.①求证△ADB≌△AOB;②求点H的坐标.(3)记K为矩形AOBC对角线的交点,S为△KDE的面积,求S的取值范围(直接写出结果即可).【答案】(1)D(1,3);(2)①详见解析;②H(175,3);(3)30334-≤S 30334+【解析】【分析】(1)如图①,在Rt△ACD中求出CD即可解决问题;(2)①根据HL证明即可;②,设AH=BH=m,则HC=BC-BH=5-m,在Rt△AHC中,根据AH2=HC2+AC2,构建方程求出m即可解决问题;(3)如图③中,当点D在线段BK上时,△DEK的面积最小,当点D在BA的延长线上时,△D′E′K的面积最大,求出面积的最小值以及最大值即可解决问题;【详解】(1)如图①中,∵A(5,0),B(0,3),∴OA=5,OB=3,∵四边形AOBC是矩形,∴AC=OB=3,OA=BC=5,∠OBC=∠C=90°,∵矩形ADEF是由矩形AOBC旋转得到,∴AD=AO=5,在Rt△ADC中,CD=22=4,AD AC∴BD=BC-CD=1,∴D(1,3).(2)①如图②中,由四边形ADEF是矩形,得到∠ADE=90°,∵点D在线段BE上,∴∠ADB=90°,由(1)可知,AD=AO,又AB=AB,∠AOB=90°,∴Rt△ADB≌Rt△AOB(HL).②如图②中,由△ADB≌△AOB,得到∠BAD=∠BAO,又在矩形AOBC中,OA∥BC,∴∠CBA=∠OAB,∴∠BAD=∠CBA,∴BH=AH,设AH=BH=m,则HC=BC-BH=5-m,在Rt△AHC中,∵AH2=HC2+AC2,∴m2=32+(5-m)2,∴m=17,5∴BH=175,∴H(175,3).(3)如图③中,当点D在线段BK上时,△DEK的面积最小,最小值=12•DE•DK=12×3×(5-342)=303344-,当点D在BA的延长线上时,△D′E′K的面积最大,最大面积=12×D′E′×KD′=12×3×(5+342)=303344+.综上所述,303344-≤S≤303344+.【点睛】本题考查四边形综合题、矩形的性质、勾股定理、全等三角形的判定和性质、旋转变换等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会利用参数构建方程解决问题.5.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.(1)求证:四边形ABCD是矩形.(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.【答案】(1)见解析;(2)18°.【解析】【分析】(1)根据平行四边形的判定得出四边形ABCD是平行四边形,求出∠ABC=90°,根据矩形的判定得出即可;(2)求出∠FDC的度数,根据三角形内角和定理求出∠DCO,根据矩形的性质得出OD=OC,求出∠CDO,即可求出答案.【详解】(1)证明:∵AO=CO,BO=DO∴四边形ABCD是平行四边形,∴∠ABC=∠ADC,∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴四边形ABCD是矩形;(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,∴∠FDC=36°,∵DF⊥AC,∴∠DCO=90°﹣36°=54°,∵四边形ABCD是矩形,∴OC=OD,∴∠ODC=54°∴∠BDF=∠ODC﹣∠FDC=18°.【点睛】本题考查了平行四边形的性质和判定,矩形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:矩形的对角线相等,有一个角是直角的平行四边形是矩形.6.已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.(1)求证:△DOE≌△BOF.(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.【答案】(1)证明见解析;(2)当∠DOE=90°时,四边形BFED为菱形,理由见解析.【解析】试题分析:(1)利用平行四边形的性质以及全等三角形的判定方法得出△DOE≌△BOF (ASA);(2)首先利用一组对边平行且相等的四边形是平行四边形得出四边形EBFD是平行四边形,进而利用垂直平分线的性质得出BE=ED,即可得出答案.试题解析:(1)∵在▱ABCD中,O为对角线BD的中点,∴BO=DO,∠EDB=∠FBO,在△EOD 和△FOB 中,∴△DOE ≌△BOF (ASA );(2)当∠DOE=90°时,四边形BFDE 为菱形,理由:∵△DOE ≌△BOF ,∴OE=OF ,又∵OB=OD ,∴四边形EBFD 是平行四边形, ∵∠EOD=90°,∴EF ⊥BD ,∴四边形BFDE 为菱形.考点:平行四边形的性质;全等三角形的判定与性质;菱形的判定.7.已知矩形纸片OBCD 的边OB 在x 轴上,OD 在y 轴上,点C 在第一象限,且86OB OD ==,.现将纸片折叠,折痕为EF (点E ,F 是折痕与矩形的边的交点),点P 为点D 的对应点,再将纸片还原。
2020年中考数学考点提分专题二十二 以特殊的平行四边形为背景的证明与计算(解析版)

2020年中考数学考点提分专题二十二以特殊的平行四边形为背景的证明与计算(解析版)考点分析【例1】(2020·安徽初三)(已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.(1)求证:四边形AFCE是菱形;(2)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长;(3)在线段AC上是否存在一点P,使得2AE2=AC·AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.【例2】(2019·江苏泰州中学附属初中初三月考)如图,正方形ABCD的边长为6,把一个含30°的直角三角形BEF放在正方形上,其中∠FBE=30°,∠BEF=90°,BE=BC,绕B点转动△FBE,在旋转过程中,(1)如图1,当F点落在边AD上时,求∠EDC的度数;(2)如图2,设EF与边AD交于点M,FE的延长线交DC于G,当AM=2时,求EG的长;(3)如图3,设EF与边AD交于点N,当tan∠ECD=13时,求△NED的面积.考点集训1.(2020·陕西初三期中)问题:如图①,在等边三角形ABC内有一点P,且PA=2,PB=63PC=1,求∠BPC的度数和等边三角形ABC的边长.李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图②),连接PP′,可得△P′PB 是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),可得∠AP′B=°,所以∠BPC =∠AP′B=°,还可证得△ABP是直角三角形,进而求出等边三角形ABC的边长为,问题得到解决.(1)根据李明同学的思路填空:∠AP′B=°,∠BPC=∠AP′B=°,等边三角形ABC的边长为.(2)探究并解决下列问题:如图③,在正方形ABCD内有一点P,且PA=5,PB=2,PC=1.求∠BPC 的度数和正方形ABCD的边长.2.(2019·云南初三月考)如图,矩形ABCD中,AB=4,AD=3,E是边AB上一点,将△CBE沿直线CE对折,得到△CFE,连接DF.(1)当D、E、F三点共线时,证明:DE=CD;(2)当BE=1时,求△CDF的面积;(3)若射线DF交线段AB于点P,求BP的最大值.3.(2019·江苏初二期末)如图1,正方形ABCD的边长为4,对角线AC、BD交于点M.(1)直接写出AM=;(2)P是射线AM上的一点,Q是AP的中点,设PQ=x.①AP=,AQ=;②以PQ为对角线作正方形,设所作正方形与△ABD公共部分的面积为S,用含x的代数式表示S,并写出相应的x的取值范围.(直接写出,不需要写过程)4.(2019·江苏初二期末)(1)如图1,已知正方形ABCD,点M和N分别是边BC,CD上的点,且BM=CN,连接AM和BN,交于点P.猜想AM与BN的位置关系,并证明你的结论;(2)如图2,将图(1)中的△APB绕着点B逆时针旋转90º,得到△A′P′B,延长A′P′交AP于点E,试判断四边形BPEP′的形状,并说明理由.5.(2020·山东初三期末)如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG,过点A作AH∥DG,交BG于点H.连接HF,AF,其中AF交EC于点M.(1)求证:△AHF为等腰直角三角形.(2)若AB=3,EC=5,求EM的长.6.(2020·深圳市龙岗区石芽岭学校初三月考)如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.(1)求证:CM=CN;(2)若△CMN的面积与△CDN的面积比为3:1,求的值.7.(2020·河南初三)如下图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F.另一边交CB的延长线于点G.(1)观察猜想:线段EF 与线段EG 的数量关系是 ;(2)探究证明:如图2,移动三角板,使顶点E 始终在正方形ABCD 的对角线AC 上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由: (3)拓展延伸:如图3,将(2)中的“正方形ABCD ”改为“矩形ABCD ”,且使三角板的一边经过点B ,其他条件不变,若AB a =、BC b ,求EF EG的值. 8.(2020·江苏初二期中)如图,长方形纸片ABCD 中,AB =8,将纸片折叠,使顶点B 落在边AD 上的E 点处,折痕的一端G 点在边BC 上.(1)如图1,当折痕的另一端F 在AB 边上且AE =4时,求AF 的长;(2)如图2,当折痕的另一端F 在AD 边上且BG =10时,①求证:△EFG 是等腰三角形;②求AF 的长;(3)如图3,当折痕的另一端F 在AD 边上,B 点的对应点E 到AD 的距离是4,且BG =5时,求AF 的长.9.(2019·河南初三期中)正方形ABCD 与正方形DEFG 按如图1放置,点A ,D ,G 在同一条直线上,点E 在CD 边上,AD =3,DE 2,连接AE ,CG .(1)线段AE 与CC 的关系为______;(2)将正方形DEFG 绕点D 顺时针旋转一个锐角后,如图2,请问(1)中的结论是否仍然成立?请说明理由(3)在正方形DEFG 绕点D 顺时针旋转一周的过程中,当∠AEC =90°时,请直接写出AE 的长.10.(2019·云南初三)如图,在矩形ABCD 中,E 是AB 边的中点,沿EC 对折矩形ABCD ,使B 点落在点P 处,折痕为EC ,连结AP 并延长AP 交CD 于F 点,(1)求证:△CBE ≌△CPE ;(2)求证:四边形AECF 为平行四边形;(3)若矩形ABCD 的边AB =6,BC =4,求△CPF 的面积.11.(2019·江西初三期中)在正方形ABCD 中,点P 是CD 上一动点,连结PA ,分别过点B 、•D•作BE ⊥PA 、DF ⊥PA ,垂足为E 、F ,如图①.(1)请探索BE 、DF 、EF 这三条线段长度具有怎样的数量关系,若点P 在DC 的延长线上(如图②),那么这三条线段的长度之间又有怎样的数量关系?若点P 在CD 的延长线上呢(如图③)?请分别直接写出结论.(2)请在(1)中的三个结论中选择一个加以证明.12.(2020·河北初三期末)如图,在正方形ABCD 中,点M 是边BC 上的一点(不与B 、C 重合),点N 在CD 的延长线上,且满足90MAN ∠=︒,连接MN 、AC ,MN 与边AD 交于点E .(1)求证:AM AN =;(2)如果2CAD NAD ∠=∠,求证:2AN AE AC =⋅.2020年中考数学考点提分专题二十二以特殊的平行四边形为背景的证明与计算(解析版)考点分析【例1】(2020·安徽初三)(已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.(1)求证:四边形AFCE是菱形;(2)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长;(3)在线段AC上是否存在一点P,使得2AE2=AC·AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.【答案】(1)证明见解析;(2)24cm;(3)存在,过E作EP⊥AD交AC于P,则P就是所求的点,证明见解析.【解析】解:(1)∵四边形ABCD是矩形,∴AD∥BC,∴∠EAO=∠FCO,由折叠的性质可得:OA=OC,AC⊥EF,在△AOE和△COF中,∵EAO FCO OA OCAOE COF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AOE≌△COF(ASA),∴AE=CF,∴四边形AFCE是平行四边形,∵AC⊥EF,∴四边形AFCE是菱形;(2)∵四边形AFCE是菱形,∴AF=AE=10cm,∵四边形ABCD是矩形,∴∠B=90°,∴S△ABF=12AB•BF=24cm2,∴AB•BF=48(cm2),∴AB2+BF2=(AB+BF)2-2AB•BF=(AB+BF)2-2×48=AF2=100(cm2),∴AB+BF=14(cm)∴△ABF的周长为:AB+BF+AF=14+10=24(cm).(3)证明:过E作EP⊥AD交AC于P,则P就是所求的点.当顶点A与C重合时,折痕EF垂直平分AC,∴OA=OC,∠AOE=∠COF=90°,∵在平行四边形ABCD中,AD∥BC,∴∠EAO=∠FCO,∴△AOE≌△COF,∴OE=OF∴四边形AFCE是菱形.∴∠AOE=90°,又∠EAO=∠EAP,由作法得∠AEP=90°,∴△AOE∽△AEP,∴AE AOAP AE,则AE2=AO•AP,∵四边形AFCE是菱形,∴AO=12 AC,∴AE2=12 AC•AP,∴2AE2=AC•AP.【点睛】本题考查翻折变换(折叠问题);菱形的判定;矩形的性质,相似三角形的判定和性质,综合性较强,掌握相关性质定理,正确推理论证是解题关键.【例2】(2019·江苏泰州中学附属初中初三月考)如图,正方形ABCD的边长为6,把一个含30°的直角三角形BEF放在正方形上,其中∠FBE=30°,∠BEF=90°,BE=BC,绕B点转动△FBE,在旋转过程中,(1)如图1,当F点落在边AD上时,求∠EDC的度数;(2)如图2,设EF与边AD交于点M,FE的延长线交DC于G,当AM=2时,求EG的长;(3)如图3,设EF与边AD交于点N,当tan∠ECD=13时,求△NED的面积.【答案】(1)15°;(2)3;(3)18 5【解析】解:(1)如图1中,作EH⊥BC于H,EM⊥CD于M.则四边形EMCH是矩形.∵四边形ABCD是正方形,∴BA=BC=CD,∠ABC=∠BCD=90°,∵BC=BE,∴AB=BE=CD,在Rt△BFA和Rt△BFE中,BF BF AB BE=⎧⎨=⎩,∴Rt△BFA≌△Rt△BFE(HL),∴∠ABF=∠EBF=30°,∵∠ABC=90°,∴∠EBC=30°,∴EH=MC=12BE=12CD,∴DM=CM,∵EM⊥CD,∴ED=EC,∵∠BCE=12(180°﹣30°)=75°,∴∠EDC=∠ECD=15°.(2)如图2中,连接BM、BG.∵AM=2,∴DM=AD﹣AM=4,由(1)可知△BMA≌△BME,△BGE≌△BGC,∴AM=EM=2,EG=CG,设EG=CG=x,则DG=6﹣x.在Rt△DMG中,MG2=DG2+DM2,∴(2+x)2=(6﹣x)2+42,∴x=3,∴EG=3.(3)如图3中,连接BN,延长FE交CD于G,连接BG.AN=NE,EG=CG,∵BE=BC,∴BG垂直平分CE,∴∠ECG+∠BCG=90°,∵∠GBC+∠ECB=90°,∴∠ECD=∠GCB,∴tan∠GBC=tan∠ECD=13,∴CGBC=13,∴CG=13BC=2,∵CD=6,∴DG=CD﹣CG=4,设AN=EN=y,则DN=6﹣y,在Rt△DNG中,(6﹣y)2+42=(2+y)2,解得:y=3,∴AN=NE=3,DN=3,NG=5,∴S△NED=35•S△DNG=35×12×3×4=185.【点睛】本题是四边形综合题,考查了正方形的性质、全等三角形的判定和性质、勾股定理、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.考点集训1.(2020·陕西初三期中)问题:如图①,在等边三角形ABC内有一点P,且PA=2,PB=PC=1,求∠BPC的度数和等边三角形ABC的边长.李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图②),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),可得∠AP′B=°,所以∠BPC =∠AP′B=°,还可证得△ABP是直角三角形,进而求出等边三角形ABC的边长为,问题得到解决.(1)根据李明同学的思路填空:∠AP′B=°,∠BPC=∠AP′B=°,等边三角形ABC的边长为.(2)探究并解决下列问题:如图③,在正方形ABCD内有一点P,且PA PB,PC=1.求∠BPC 的度数和正方形ABCD的边长.【答案】(1)∠AP′B =150°,∠BPC =∠AP′B =150°,等边三角形ABC 7;(2)∠BPC =135°,正方形ABCD 5【解析】(1)∵等边△ABC ,∴∠ABC=60°,将△BPC 绕点B 逆时针旋转60°得出△ABP′,∴AP′=CP=1,3,∠PBC=∠P′BA ,∠AP′B=∠BPC ,∵∠PBC+∠ABP=∠ABC=60°,∴∠ABP′+∠ABP=∠ABC=60°,∴△BPP′是等边三角形,∴3BP′P=60°,∵AP′=1,AP=2,∴AP′2+PP′2=AP 2,∴∠AP′P=90°,∴∠BPC=∠AP′B=90°+60°=150°,过点B 作BM ⊥AP′,交AP′的延长线于点M ,∴∠MP′B=30°,BM=32由勾股定理得:P′M=32, ∴AM=1+32=52, 由勾股定理得:22=7AM BM故答案为:150°7(2)将△BPC绕点B逆时针旋转90°得到△AEB,与(1)类似:可得:AE=PC=1,2,∠BPC=∠AEB,∠ABE=∠PBC,∴∠EBP=∠EBA+∠ABP=∠ABC=90°,∴∠BEP=12(180°-90°)=45°,由勾股定理得:EP=2,∵AE=1,5EP=2,∴AE2+PE2=AP2,∴∠AEP=90°,∴∠BPC=∠AEB=90°+45°=135°,过点B作BF⊥AE,交AE的延长线于点F;∴∠FEB=45°,∴FE=BF=1,∴AF=2;∴在Rt△ABF中,由勾股定理,得5∴∠BPC=135°5答:∠BPC的度数是135°,正方形ABCD5【点睛】本题主要考查对勾股定理及逆定理,等边三角形的性质和判定,等腰三角形的性质,含30度角的直角三角形的性质,正方形的性质,旋转的性质等知识点的理解和掌握,正确作辅助线并能根据性质进行证明是解此题的关键.2.(2019·云南初三月考)如图,矩形ABCD中,AB=4,AD=3,E是边AB上一点,将△CBE沿直线CE对折,得到△CFE,连接DF.(1)当D、E、F三点共线时,证明:DE=CD;(2)当BE=1时,求△CDF的面积;(3)若射线DF交线段AB于点P,求BP的最大值.【答案】(1)见解析;(2)245;(3)47【解析】证明:(1)∵四边形ABCD是矩形∴AB=CD=4,AD=BC=3,AB∥CD,∴∠DCE=∠CEB∵△CBE翻折得到△CFE∴∠FEC=∠CEB∴∠DCE=∠FEC∴DE=CD(2)如图1,延长EF交CD的延长线于点G,∵四边形ABCD是矩形∴AB=CD=4,AD=BC=3,AB∥CD,∴∠DCE=∠CEB∵△CBE翻折得到△CFE∴∠FEC=CEB,CF=BC=3,EF=BE=1,∠CFE=90°∴∠DCE=∠FEC,∠CFG=90°∴CG=EG,∴GF=GE﹣EF=CG﹣1∵在Rt△CGF中,CG2=CF2+GF2,∴CG2=9+(CG﹣1)2,解得:CG=5∵△CDF与△CGF分别以CD、CG为底时,高相等∴45CDFCGFS CDS CG==VV∴S△CDF=45S△CGF=413452⨯⨯⨯=245(3)如图2,过点C作CH⊥DP于点H,连接CP,∵CD∥AB∴∠CDP=∠APD,且∠A=∠CHD=90°∴△ADP∽△HCD∴CD CHDP AD==DHAP,∵CH≤CF,CF=BC=AD=3∴CH≤3∴当点H与点F重合时,CH最大,DH最小,AP最小,BP最大,此时,在△ADP与△HCDAPD CDPA CHD90AD CH︒∠=∠⎧⎪∠=∠=⎨⎪=⎩∴△ADP≌△HCD(AAS)∴CD=DP=4,AP=DF∵AP=22DP AD-=7∴BP的最大值为4﹣7.【点睛】此题主要考查相似三角形的判定与性质,解题的关键是熟知矩形的性质、勾股定理及相似三角形的判定与性质.3.(2019·江苏初二期末)如图1,正方形ABCD的边长为4,对角线AC、BD交于点M.(1)直接写出AM=;(2)P是射线AM上的一点,Q是AP的中点,设PQ=x.①AP=,AQ=;②以PQ为对角线作正方形,设所作正方形与△ABD公共部分的面积为S,用含x的代数式表示S,并写出相应的x的取值范围.(直接写出,不需要写过程)【答案】(1)2(2)①2x,x;②S222x x=-+(0<x≤2.【解析】解:(1)∵正方形ABCD的边长为4,∴对角线AC22AB==2,又∴AM12AC==2.故答案为:2.(2)①Q是AP的中点,设PQ=x,∴AP=2PQ=2x,AQ=x.故答案为:2x;x.②如图:∵以PQ为对角线作正方形,∴∠GQM=∠FQM=45°∵正方形ABCD对角线AC、BD交于点M,∴∠FMQ=∠GMQ=90°,∴△FMQ和△GMQ均为等腰直角三角形,∴FM=QM=MG.∵QM=AM﹣2x,∴S12=FG•QM()12222x x=⋅,∴S222x x=-+,∵依题意得:20xx⎧⎪⎨⎪⎩>>,∴0<2,综上所述:S222x x=-+(0<2),【点睛】本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角.解答本题要充分利用等腰直角三角形性质解答.4.(2019·江苏初二期末)(1)如图1,已知正方形ABCD,点M和N分别是边BC,CD上的点,且BM=CN,连接AM和BN,交于点P.猜想AM与BN的位置关系,并证明你的结论;(2)如图2,将图(1)中的△APB绕着点B逆时针旋转90º,得到△A′P′B,延长A′P′交AP于点E,试判断四边形BPEP′的形状,并说明理由.【答案】(1)AM⊥BN,证明见解析;(2)四边形BPEP′是正方形,理由见解析.【解析】(1)AM⊥BN证明:∵四边形ABCD是正方形,∴AB=BC,∠ABM=∠BCN=90°∵BM=CN,∴△ABM≌△BCN∴∠BAM=∠CBN∵∠CBN+∠ABN=90°,∴∠ABN+∠BAM=90°,∴∠APB=90°∴AM⊥BN.(2)四边形BPEP′是正方形.△A′P′B是△APB绕着点B逆时针旋转90º所得,∴BP= BP′,∠P′BP=90º.又由(1)结论可知∠APB=∠A′P′B=90°,∴∠BP′E=90°.所以四边形BPEP′是矩形.又因为BP= BP′,所以四边形BPEP′是正方形.【点睛】此题主要考查特殊平行四边形的性质与判定,解题的关键是熟知正方形的性质与判定.5.(2020·山东初三期末)如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG,过点A作AH ∥DG,交BG于点H.连接HF,AF,其中AF交EC于点M.(1)求证:△AHF为等腰直角三角形.(2)若AB=3,EC=5,求EM的长.【答案】(1)见解析;(2)EM=5 4【解析】证明:(1)∵四边形ABCD,四边形ECGF都是正方形∴DA∥BC,AD=CD,FG=CG,∠B=∠CGF=90°∵AD∥BC,AH∥DG,∴四边形AHGD是平行四边形∴AH=DG,AD=HG=CD,∵CD=HG,∠ECG=∠CGF=90°,FG=CG,∴△DCG≌△HGF(SAS),∴DG=HF,∠HFG=∠HGD∴AH=HF,∵∠HGD+∠DGF=90°,∴∠HFG+∠DGF=90°∴DG⊥HF,且AH∥DG,∴AH⊥HF,且AH=HF∴△AHF为等腰直角三角形.(2)∵AB=3,EC=5,∴AD=CD=3,DE=2,EF=5.∵AD∥EF,∴53EM EFDM AD==,且DE=2.∴EM=54.【点睛】本题考查了正方形的性质,平行四边形的判定和性质,全等三角形的判定和性质,平行线分线段成比例等知识点,综合性较强难度大灵活运用这些知识进行推理是本题的关键.6.(2020·深圳市龙岗区石芽岭学校初三月考)如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.(1)求证:CM=CN;(2)若△CMN的面积与△CDN的面积比为3:1,求的值.【答案】(1)证明见解析;(2)23【解析】解:(1)证明:由折叠的性质可得:∠ANM=∠CNM,∵四边形ABCD是矩形,∴AD∥BC.∴∠ANM=∠CMN.∴∠CMN=∠CNM.∴CM=CN.(2)过点N作NH⊥BC于点H,则四边形NHCD是矩形.∴HC=DN,NH=DC.∵△CMN的面积与△CDN的面积比为3:1,∴12312CMNCDNMC NHS MCS NDDN NH===VVgg.∴MC=3ND=3HC.∴MH=2HC.设DN=x,则HC=x,MH=2x,∴CM=3x=CN.在Rt △CDN 中,2222DC CN DN x =-=,∴HN=22x .在Rt △MNH 中,2223MN MH HN x =+=,∴2323MN x DF x==. 7.(2020·河南初三)如下图1,将三角板放在正方形ABCD 上,使三角板的直角顶点E 与正方形ABCD 的顶点A 重合,三角板的一边交CD 于点F .另一边交CB 的延长线于点G .(1)观察猜想:线段EF 与线段EG 的数量关系是 ;(2)探究证明:如图2,移动三角板,使顶点E 始终在正方形ABCD 的对角线AC 上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:(3)拓展延伸:如图3,将(2)中的“正方形ABCD ”改为“矩形ABCD ”,且使三角板的一边经过点B ,其他条件不变,若AB a =、BC b =,求EF EG的值. 【答案】(1)EF EG =;(2)成立,证明过程见解析;(3)EF b EG a =. 【解析】(1)EF EG =,理由如下:由直角三角板和正方形的性质得90ED EB D EBC BED GEF =⎧⎨∠=∠=∠=∠=︒⎩9090FED BEF GEB BEF D EBG ∠+∠=∠+∠=︒⎧∴⎨∠=∠=︒⎩ FED GEB ∴∠=∠在FED ∆和GEB ∆中,90FED GEB ED EBD EBG ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩()FED GEB ASA ∴∆≅∆EF EG ∴=;(2)成立,证明如下:如图,过点E 分别作,EH BC EI CD ⊥⊥,垂足分别为,H I ,则四边形EHCI 是矩形90HEI ∴∠=︒90,90FEI HEF GEH HEF ∴∠+∠=︒∠+∠=︒FEI GEH ∴∠=∠由正方形对角线的性质得,AC 为BCD ∠的角平分线则EI EH =在FEI ∆和GEH ∆中,90FEI GEH EI EHFIE GHE ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩()FEI GEH ASA ∴∆≅∆EF EG ∴=;(3)如图,过点E 分别作,EM BC EN CD ⊥⊥,垂足分别为,M N同(2)可知,FEN GEM ∠=∠由长方形性质得:90,90,D ENC ABC EMC AD BC b ∠=∠=︒∠=∠=︒==//,//EN AD EM AB ∴,CEN CAD CEM CAB ∴∆~∆∆~∆,EN CE EM CE AD CA AB CA∴== EN EM AD AB ∴=,即EN AD b EM AB a== 在FEN ∆和GEM ∆中,90FEN GEM FNE GME ∠=∠⎧⎨∠=∠=︒⎩∴∆~∆FEN GEMEF EN b∴==.EG EM a【点睛】本题考查了正方形的性质、矩形的性质、三角形全等的判定定理与性质、相似三角形的判定定理与性质,较难的是题(3),通过作辅助线,构造两个相似三角形是解题关键.8.(2020·江苏初二期中)如图,长方形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD上的E点处,折痕的一端G点在边BC上.(1)如图1,当折痕的另一端F在AB边上且AE=4时,求AF的长;(2)如图2,当折痕的另一端F在AD边上且BG=10时,①求证:△EFG是等腰三角形;②求AF的长;(3)如图3,当折痕的另一端F在AD边上,B点的对应点E到AD的距离是4,且BG=5时,求AF的长.【答案】(1)AF=3;(2)①见解析;②AF=6;(3)AF=1【解析】(1)解:∵纸片折叠后顶点B落在边AD上的E点处,∴BF=EF,∵AB=8,∴EF=8﹣AF,在Rt△AEF中,AE2+AF2=EF2,即42+AF2=(8﹣AF)2,解得AF=3;(2)①证明:∵纸片折叠后顶点B落在边AD上的E点处,∴∠BGF=∠EGF,∵长方形纸片ABCD的边AD∥BC,∴∠BGF=∠EFG,∴∠EGF=∠EFG,∴EF=EG,∴△EFG是等腰三角形;②解:∵纸片折叠后顶点B落在边AD上的E点处,∴EG=BG=10,HE=AB=8,FH=AF,∴EF=EG=10,在Rt△EFH中,FH=2222108EF HE-=-=6,∴AF=FH=6;(3)解:如图3,设EH与AD相交于点K,过点E作MN∥CD分别交AD、BC于M、N,∵E到AD的距离为4,∴EM=4,EN=8﹣4=4,在Rt△ENG中,EG=BG=5,∴GN222254EG EN-=-3,∵∠GEN+∠KEM=180°﹣∠GEH=180°﹣90°=90°,∠GEN+∠NGE=180°﹣90°=90°,∴∠KEM=∠NGE,又∵∠ENG=∠KME=90°,∴△GEN∽△EKM,∴EK KM EM EG EN GN==,即4 543 EK KM==,解得EK=203,KM=163,∴KH=EH﹣EK=8﹣203=43,∵∠FKH=∠EKM,∠H=∠EMK=90°,∴△FKH∽△EKM,∴FH KHEM KM=,即431643FH=,解得FH=1,∴AF=FH=1.【点睛】此题考查折叠的性质,勾股定理,相似三角形的判定及性质定理,每个小问的问题都是求AF的长度,故解题中注意思路和方法的总结,(3)中的解题思路与(2)相类似,求出FH问题得解,故将问题转化是解题的一种特别重要的思路.9.(2019·河南初三期中)正方形ABCD与正方形DEFG按如图1放置,点A,D,G在同一条直线上,点E 在CD边上,AD=3,DE=2,连接AE,CG.(1)线段AE与CC的关系为______;(2)将正方形DEFG绕点D顺时针旋转一个锐角后,如图2,请问(1)中的结论是否仍然成立?请说明理由(3)在正方形DEFG绕点D顺时针旋转一周的过程中,当∠AEC=90°时,请直接写出AE的长.【答案】(1)AE=CG,AE⊥CG;(2)仍然成立;理由见解析;(3)AE的长为2+1或2﹣1.【解析】(1)线段AE与CG的关系为:AE=CG,AE⊥CG,理由如下:如图1,延长AE交CG于点H,∵四边形ABCD和四边形DGFE是正方形,∴AD=CD,ED=GD,∠ADE=∠CDG=90°,∴△ADE≌△CDG(SAS),∴AE=CG,∠EAD=∠GCD,∵∠EAD+∠AED=90°,∠AED=∠CEH,∴∠GCD+∠CEH=90°,∴∠CHE=90°,即AE⊥CG,故答案为:AE=CG,AE⊥CG;(2)结论仍然成立,理由如下:如图2,设AE与CG交于点H,∵四边形ABCD和四边形DGFE是正方形,∴AD=CD,ED=GD,∠ADC=∠EDG=90°,∴∠ADC+∠CDE=∠EDG+∠CDE,即∠ADE=∠CDG,∴△ADE≌△CDG(SAS),∴AE=CG,∠EAD=∠GCD,∵∠EAD+∠APD=90°,∠APD=∠CPH,∴∠GCD+∠CPH=90°,∴∠CHP=90°,即AE⊥CG,∴AE=CG,AE⊥CG,∴①中的结论仍然成立;(3)如图3﹣1,当点E旋转到线段CG上时,过点D作DM⊥AE于点M,∵∠AEC=90°,∠DEG=45°,∴∠AED=45°,∴Rt△DME是等腰直角三角形,DE=1,∴ME=MD=2在Rt⊈△AMD中,ME=1,AD=3,∴AM,∴AE =AM+ME =22+1; 如图3﹣2,当点E 旋转到线段CG 的延长线上时,过点D 作DN ⊥CE 于点N ,则∠END =90°,∵∠DEN =45°,∴∠EDN =45°,∴Rt △DNE 是等腰直角三角形,∴NE =ND =22DE =1, 在Rt △CND 中,ND =1,CD =3,∴CN =22CD ND -=2231-=22,∴CE =NE+CN =22+1,∵AC =2AD =32,∴在Rt △AEC 中,AE =22AC CE -=22(32)(221)-+=22﹣1,综上所述,AE 的长为22+1或22﹣1.【点睛】本题考查全等三角形的判定(SAS )与性质,正方形的性质,旋转的性质以及勾股定理,解题关键是在第(3)问中能够根据题意分情况讨论并画出图形,才能保证解答的完整性.10.(2019·云南初三)如图,在矩形ABCD 中,E 是AB 边的中点,沿EC 对折矩形ABCD ,使B 点落在点P 处,折痕为EC ,连结AP 并延长AP 交CD 于F 点,(1)求证:△CBE ≌△CPE ;(2)求证:四边形AECF 为平行四边形;(3)若矩形ABCD 的边AB =6,BC =4,求△CPF 的面积.【答案】(1)见解析;(2)见解析;(3)4225【解析】 (1)解:由折叠可知,EP =EB ,CP =CB ,∵EC =EC ,∴△ECP ≌△ECB (SSS ).(2)证明:由折叠得到BE =PE ,EC ⊥PB ,∵E 为AB 的中点,∴AE =EB =PE ,∴AP ⊥BP ,∴AF ∥EC ,∵AE ∥FC ,∴四边形AECF 为平行四边形;(3)过P 作PM ⊥DC ,交DC 于点M ,在Rt △EBC 中,EB =3,BC =4, 根据勾股定理得:2222345EC EB BC =+=+=1122EBC S EB BQ EC BQ =⋅=⋅V Q ,341255EB BC BQ EC ⋅⨯∴===, 由折叠得:BP =2BQ =245, 在Rt △ABP 中,AB =6,BP =245, 根据勾股定理得: 22222418655AP AB BP ⎛⎫=-=-= ⎪⎝⎭, ∵四边形AECF 为平行四边形,∴AF =EC =5,FC =AE =3,∴PF =5﹣185=75, ∵PM ∥AD ,∴△FPM ∽△FADPF PM AF AD ∴=,即7554PM = 解得:PM =2825, 则S △PFC =12FC•PM =12×3×2825=4225.【点睛】本题考查的是利用折叠性质来证明三角形全等和平行四边形四边形,还考查了利用勾股定理、面积公式来求三角形的边长,利用相似三角形的性质对应边成比例来求出三角形的高,进而求出三角形的面积.本题第(3)中求也可利用△APB ∽△EBC ,对应边成比例AP BA BE EC=,求AP ,这样比较简便. 11.(2019·江西初三期中)在正方形ABCD 中,点P 是CD 上一动点,连结PA ,分别过点B 、•D•作BE ⊥PA 、DF ⊥PA ,垂足为E 、F ,如图①.(1)请探索BE 、DF 、EF 这三条线段长度具有怎样的数量关系,若点P 在DC 的延长线上(如图②),那么这三条线段的长度之间又有怎样的数量关系?若点P 在CD 的延长线上呢(如图③)?请分别直接写出结论.(2)请在(1)中的三个结论中选择一个加以证明.【答案】(1)图①中,BE=DF+EF ;图②中,BE=DF-EF ;图③中,BE=EF-DF ;(2)见解析【解析】解:(1)在正方形ABCD 中,AB=AD,∠BAD=90°,∴∠BAE+∠DAF=90°,∵BE ⊥PA ,DF ⊥PA ,∴∠AEB=∠DFA=90°,∠ABE+∠BAE=90°,∴∠ABE=∠DAF ,在△ABE 和△DAF 中,90ABE DAF AEB DFA AB AD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△ABE ≌△DAF(AAS),∴AE=DF ,AF=BE ,如图①,∵AF=AE+EF ,∴BE=DF+EF ,如图②,∵AE=AF+EF ,∴BE = DF -EF ,如图③,∵EF=AE+AF ,∴BE = EF -DF(2)证明:如图题①,∵ABCD 是正方形,∴AB=AD ,∵BE ⊥PA ,DF ⊥PA ,∴∠AEB=∠AFD=90°,∠ABE+∠BAE=90°.∵∠DAF+∠BAE=90°,∴∠ABE=∠DAF ,∴Rt △ABE ≌Rt △DAF ,∴BE=AF ,AE=DF ,而AF=AE+EF ,∴BE=DF+EF ;【点睛】本题主要考查了正方形的性质,全等三角形的判定与性质,掌握正方形的性质,全等三角形的判定与性质是解题的关键.12.(2020·河北初三期末)如图,在正方形ABCD 中,点M 是边BC 上的一点(不与B 、C 重合),点N 在CD 的延长线上,且满足90MAN ∠=︒,连接MN 、AC ,MN 与边AD 交于点E .(1)求证:AM AN =;(2)如果2CAD NAD ∠=∠,求证:2AN AE AC =⋅.【答案】(1)见解析;(2)见解析【解析】解:证明(1)∵四边形ABCD 是正方形,∴AB =AD ,∠CAD =∠ACB =45°,∠BAD =∠CDA =∠B =90°,∴∠BAM +∠MAD =90°,∠ADN =90°∵∠MAN =90°,∴∠MAD +∠DAN =90°,∴∠BAM =∠DAN ,且AD=AB,∠ABC=∠ADN=90°∴△ABM≌△ADN(ASA)∴AM=AN,(2)∵AM=AN,∠MAN=90°,∴∠MNA=45°,∵∠CAD=2∠NAD=45°,∴∠NAD=22.5°∴∠CAM=∠MAN﹣∠CAD﹣∠NAD=22.5°∴∠CAM=∠NAD,∠ACB=∠MNA=45°,∴△AMC∽△AEN∴ANAC=AEAM,且AN=AM,∴AN2=AE•AC【点睛】本题主要考查正方形的性质,全等三角形和相似三角形的判定及性质,掌握正方形的性质,全等三角形和相似三角形的判定及性质是解题的关键.。
特殊平行四边形考点分析

特殊平行四边形考点分析徐州市撷秀中学初二数学组 魏加鸿八年级本周进入特殊平行四边形单元的学习,特殊四边形的判定和性质是中考要考查的重点内容之一,以选择题、填空题及解答题的形式出现。
选择题、填空题主要考查各种图形性质的区别及判定的条件,解答题则综合利用各种知识证明线段相等或解决其他问题。
下面就本章节知识在中考中的情况进行如下分析:一、考纲要求:1、掌握矩形、菱形、正方形的概念,了解它们之间的关系;2、掌握矩形、菱形、正方形的性质和四边形是矩形、菱形、正方形的条件二、近三年徐州中考中出现的题型、分值及考点2011年9.(2的正方形ABCD 沿对角线AC 平移,使点A 移至线段AC 的中点A '处,得新正方形A B C D '''',新正方形与原正方形重叠部分(图中阴影部分)的面积是( )B .12C .1D .14考点分析:平移的性质;正方形的性质28.(12分)如图,已知二次函数2y x bx c =++的图象与x 轴交于A B 、两点,与y 轴交于点P ,顶点为()12C -,.(1)求此函数的关系式;(2)作点C 关于x 轴的对称点D ,顺次连结A C B D 、、、.若在抛物线上存在点E ,使直线PE 将四边形ACBD 分成面积相等的两个四边形,求点E 的坐标.(3)在(2)的条件下,抛物线上是否存在一点F ,使得PEF △是以P 为直角顶点的直角三角形?若存在,求出点F 的坐标及PEF △的面积;若不存在,请说明理由.考点分析:本题是二次函数的综合题,其中涉及的到的知识点有抛物线的公式的求法及三角形的相似、菱形的判定及性质等知识点,是各地中考的热点和难点,解题时注意数形结合等数学思想的运用,2012年8(3分)如图,在正方形ABCD 中,E 是CD 的中点,点F 在BC 上, 且14FC BC .图中相似三角形共有 A . 1对 B .2对C . 3对D .4对考点分析:正方形的性质、三角形相似等知识 27.( 8分)如图1,A 、B 、C 、D 为矩形的四个顶点,AD=4cm ,AB=dcm 。
中考数学与平行四边形有关的压轴题附答案解析
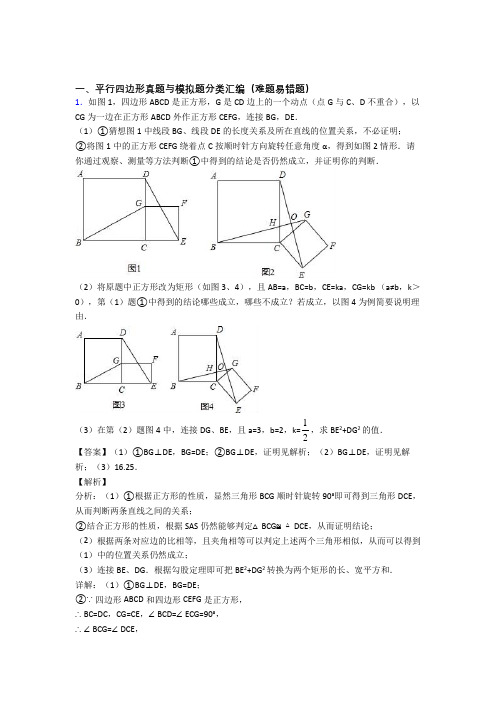
一、平行四边形真题与模拟题分类汇编(难题易错题)1.如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.(1)①猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系,不必证明;②将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度α,得到如图2情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并证明你的判断.(2)将原题中正方形改为矩形(如图3、4),且AB=a,BC=b,CE=ka,CG=kb (a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图4为例简要说明理由.(3)在第(2)题图4中,连接DG、BE,且a=3,b=2,k=12,求BE2+DG2的值.【答案】(1)①BG⊥DE,BG=DE;②BG⊥DE,证明见解析;(2)BG⊥DE,证明见解析;(3)16.25.【解析】分析:(1)①根据正方形的性质,显然三角形BCG顺时针旋转90°即可得到三角形DCE,从而判断两条直线之间的关系;②结合正方形的性质,根据SAS仍然能够判定△BCG≌△DCE,从而证明结论;(2)根据两条对应边的比相等,且夹角相等可以判定上述两个三角形相似,从而可以得到(1)中的位置关系仍然成立;(3)连接BE、DG.根据勾股定理即可把BE2+DG2转换为两个矩形的长、宽平方和.详解:(1)①BG⊥DE,BG=DE;②∵四边形ABCD和四边形CEFG是正方形,∴BC=DC,CG=CE,∠BCD=∠ECG=90°,∴∠BCG=∠DCE,∴△BCG≌△DCE,∴BG=DE,∠CBG=∠CDE,又∵∠CBG+∠BHC=90°,∴∠CDE+∠DHG=90°,∴BG⊥DE.(2)∵AB=a,BC=b,CE=ka,CG=kb,∴BC CG b==,DC CE a又∵∠BCG=∠DCE,∴△BCG∽△DCE,∴∠CBG=∠CDE,又∵∠CBG+∠BHC=90°,∴∠CDE+∠DHG=90°,∴BG⊥DE.(3)连接BE、DG.根据题意,得AB=3,BC=2,CE=1.5,CG=1,∵BG⊥DE,∠BCD=∠ECG=90°∴BE2+DG2=BO2+OE2+DO2+OG2=BC2+CD2+CE2+CG2=9+4+2.25+1=16.25.点睛:此题综合运用了全等三角形的判定和性质、相似三角形的判定和性质以及勾股定理.2.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.(1)求证:四边形BEDF是平行四边形;(2)当四边形BEDF是菱形时,求EF的长.413【答案】(1)证明见解析;(2【解析】分析:(1)根据平行四边形ABCD 的性质,判定△BOE ≌△DOF (ASA ),得出四边形BEDF 的对角线互相平分,进而得出结论;(2)在Rt △ADE 中,由勾股定理得出方程,解方程求出BE ,由勾股定理求出BD ,得出OB ,再由勾股定理求出EO ,即可得出EF 的长.详解:(1)证明:∵四边形ABCD 是矩形,O 是BD 的中点,∴∠A=90°,AD=BC=4,AB ∥DC ,OB=OD ,∴∠OBE=∠ODF ,在△BOE 和△DOF 中,OBE ODF OB ODBOE DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BOE ≌△DOF (ASA ),∴EO=FO ,∴四边形BEDF 是平行四边形;(2)当四边形BEDF 是菱形时,BD ⊥EF ,设BE=x ,则 DE=x ,AE=6-x ,在Rt △ADE 中,DE 2=AD 2+AE 2,∴x 2=42+(6-x )2,解得:x=133, ∵∴OB=12∵BD ⊥EF ,∴∴EF=2EO=3. 点睛:本题主要考查了矩形的性质,菱形的性质、勾股定理、全等三角形的判定与性质,熟练掌握矩形的性质和勾股定理,证明三角形全等是解决问的关键3.在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,且∠EAF=∠CEF=45°.(1)将△ADF 绕着点A 顺时针旋转90°,得到△ABG(如图①),求证:△AEG ≌△AEF ;(2)若直线EF 与AB ,AD 的延长线分别交于点M ,N(如图②),求证:EF 2=ME 2+NF 2;(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF ,BE ,DF 之间的数量关系.【答案】(1)证明见解析;(2)证明见解析;(3)EF2=2BE2+2DF2.【解析】试题分析:(1)根据旋转的性质可知AF=AG,∠EAF=∠GAE=45°,故可证△AEG≌△AEF;(2)将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由(1)知△AEG≌△AEF,则EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;(3)将△ADF绕着点A顺时针旋转90°,得到△ABG,根据旋转的性质可以得到△ADF≌△ABG,则DF=BG,再证明△AEG≌△AEF,得出EG=EF,由EG=BG+BE,等量代换得到EF=BE+DF.试题解析:(1)∵△ADF绕着点A顺时针旋转90°,得到△ABG,∴AF=AG,∠FAG=90°,∵∠EAF=45°,∴∠GAE=45°,在△AGE与△AFE中,,∴△AGE≌△AFE(SAS);(2)设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.则△ADF≌△ABG,DF=BG.由(1)知△AEG≌△AEF,∴EG=EF.∵∠CEF=45°,∴△BME、△DNF、△CEF均为等腰直角三角形,∴CE=CF,BE=BM,NF=DF,∴a﹣BE=a﹣DF,∴BE=DF,∴BE=BM=DF=BG,∴∠BMG=45°,∴∠GME=45°+45°=90°,∴EG2=ME2+MG2,∵EG=EF ,MG=BM=DF=NF,∴EF2=ME2+NF2;(3)EF2=2BE2+2DF2.如图所示,延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.由(1)知△AEH≌△AEF,则由勾股定理有(GH+BE)2+BG2=EH2,即(GH+BE)2+(BM﹣GM)2=EH2又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,即2(DF2+BE2)=EF2考点:四边形综合题4.如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.(1)证明:BE=CF.(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.【答案】(1)见解析;(2)43;(3)见解析【解析】试题分析:(1)先求证AB=AC,进而求证△ABC、△ACD为等边三角形,得∠4=60°,AC=AB进而求证△ABE≌△ACF,即可求得BE=CF;(2)根据△ABE≌△ACF可得S△ABE=S△ACF,故根据S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC即可解题;(3)当正三角形AEF的边AE与BC垂直时,边AE最短.△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又根据S△CEF=S四边形AECF-S△AEF,则△CEF的面积就会最大.试题解析:(1)证明:连接AC,∵∠1+∠2=60°,∠3+∠2=60°,∴∠1=∠3,∵∠BAD=120°,∴∠ABC=∠ADC=60°∵四边形ABCD是菱形,∴AB=BC=CD=AD,∴△ABC、△ACD为等边三角形∴∠4=60°,AC=AB,∴在△ABE和△ACF中,,∴△ABE≌△ACF.(ASA)∴BE=CF.(2)解:由(1)得△ABE≌△ACF,则S△ABE=S△ACF.故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值.作AH⊥BC于H点,则BH=2,S四边形AECF=S△ABC===; (3)解:由“垂线段最短”可知,当正三角形AEF 的边AE 与BC 垂直时,边AE 最短.故△AEF 的面积会随着AE 的变化而变化,且当AE 最短时,正三角形AEF 的面积会最小,又S △CEF =S 四边形AECF ﹣S △AEF ,则△CEF 的面积就会最大.由(2)得,S △CEF =S 四边形AECF ﹣S △AEF =﹣=.点睛:本题考查了菱形每一条对角线平分一组对角的性质,考查了全等三角形的证明和全等三角形对应边相等的性质,考查了三角形面积的计算,本题中求证△ABE ≌△ACF 是解题的关键.5.问题情境在四边形ABCD 中,BA =BC ,DC ⊥AC ,过点D 作DE ∥AB 交BC 的延长线于点E ,M 是边AD 的中点,连接MB ,ME.特例探究(1)如图1,当∠ABC =90°时,写出线段MB 与ME 的数量关系,位置关系;(2)如图2,当∠ABC =120°时,试探究线段MB 与ME 的数量关系,并证明你的结论; 拓展延伸(3)如图3,当∠ABC =α时,请直接用含α的式子表示线段MB 与ME 之间的数量关系.【答案】(1)MB =ME ,MB ⊥ME ;(2)ME 3.证明见解析;(3)ME =MB·tan 2 .【解析】【分析】(1)如图1中,连接CM .只要证明△MBE 是等腰直角三角形即可;(2)结论:EM=3MB .只要证明△EBM 是直角三角形,且∠MEB=30°即可; (3)结论:EM=BM•tan2 .证明方法类似;【详解】(1) 如图1中,连接CM .∵∠ACD=90°,AM=MD ,∴MC=MA=MD ,∵BA=BC ,∴BM 垂直平分AC ,∵∠ABC=90°,BA=BC ,∴∠MBE=12∠ABC=45°,∠ACB=∠DCE=45°, ∵AB ∥DE ,∴∠ABE+∠DEC=180°,∴∠DEC=90°,∴∠DCE=∠CDE=45°,∴EC=ED ,∵MC=MD ,∴EM 垂直平分线段CD ,EM 平分∠DEC ,∴∠MEC=45°,∴△BME 是等腰直角三角形,∴BM=ME ,BM ⊥EM .故答案为BM=ME ,BM ⊥EM . (2)ME =3MB .证明如下:连接CM ,如解图所示.∵DC ⊥AC ,M 是边AD 的中点,∴MC =MA =MD .∵BA =BC ,∴BM 垂直平分AC .∵∠ABC =120°,BA =BC ,∴∠MBE =12∠ABC =60°,∠BAC =∠BCA =30°,∠DCE =60°. ∵AB ∥DE ,∴∠ABE +∠DEC =180°,∴∠DEC =60°,∴∠DCE =∠DEC =60°,∴△CDE 是等边三角形,∴EC =ED .∵MC =MD ,∴EM 垂直平分CD ,EM 平分∠DEC , ∴∠MEC =12∠DEC =30°, ∴∠MBE +∠MEB =90°,即∠BME =90°.在Rt △BME 中,∵∠MEB =30°,∴ME =3MB .(3) 如图3中,结论:EM=BM•tan 2α.理由:同法可证:BM ⊥EM ,BM 平分∠ABC ,所以EM=BM•tan2α. 【点睛】本题考查四边形综合题、等腰直角三角形的判定和性质、等边三角形的判定和性质、等腰三角形的性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题.6.如图,抛物线y=mx 2+2mx+n 经过A (﹣3,0),C (0,﹣32)两点,与x 轴交于另一点B .(1)求经过A ,B ,C 三点的抛物线的解析式;(2)过点C 作CE ∥x 轴交抛物线于点E ,写出点E 的坐标,并求AC 、BE 的交点F 的坐标 (3)若抛物线的顶点为D ,连结DC 、DE ,四边形CDEF 是否为菱形?若是,请证明;若不是,请说明理由.【答案】(1)y=12x2+x﹣32;(2)F点坐标为(﹣1,﹣1);(3)四边形CDEF是菱形.证明见解析【解析】【分析】将A、C点的坐标代入抛物线的解析式中,通过联立方程组求得该抛物线的解析式;根据(1)题所得的抛物线的解析式,可确定抛物线的对称轴方程以及B、C点的坐标,由CE∥x轴,可知C、E关于对称轴对称。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、如图,一次函数 的图像与 轴分别相交于点A、B,以AB为边作正方形ABCD。
(1)求点A、B、D的坐标;
(2)设点M在 轴上,如果△ABM为等腰三角形,求点M的坐标。
(1)由几个不同的位置,分别测量BF、AG、AE的长,从中你能发现BF、AG、AE的数量之间具有怎样的关系?并证明你所得到的结论。
(2)连接DF,如果正方形的边长为2,设AE= ,△DFG的面积为 ,求 与 之间的函数解析式,并写出函数的定义域。
(3)如果正方形的边长为2,FG的长为 ,求点C到直线DE的距离。
(1)求点C的坐标(用含 的表达式表示);
(2)求 关于 的函数解析式,并写出 的取值范围;
(3)当△PBC为等腰三角形时,求点P的坐标。
10、如图,长方形ABCD中,AB=3,BC=4,E是边AD上的动点,F是射线BC上的一点,BF=EF,且交射线DC于点G,设AE= ,BF= 。
(1)当△BEF是等边三角形时,求BF的长;
8、已知,在矩形ABCD中,AB=10,BCCD边AB、BC、DA上,AE=2。
1)如图1,当四边形EFGH为正方形时,求△GFC的面积。
2)如图2,当四边形EFGH为菱形,且BF= 时,求△GFC的面积。(用含 的代数式表示)
9、如图,已知在平面直角坐标系中,点A的坐标为(0,2),点B的坐标为(2,0),经过原点的直线交线段AB于点C,过点C作OC的垂线与直线 相交于点P,设BC= ,点P的坐标为
(2)当点P在BC边上时,正方形的边长为2,设 。求 与 的函数关系式,并写出函数的定义域;
(3)在(2)的条件下,当 时,求EF的长。
4、直线 与坐标轴分别交与点A、B两点,点P、Q同时从O点出发,同时到达A点,运动停止。点Q沿线段OA运动,速度为每秒1个单位长度,点P沿 运动。
(1)直接写出A、B两点的坐标;
(2)设点Q的运动时间为 秒,△OPQ的面积为 ,求出 与 之间的函数关系式。
(3)当 时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标。
5、如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿 运动,试写出△APM的面积 与点P经过的路程 之间的函数关系,写出定义域,并画出函数图像。
(2)求 与 之间的函数解析式,并写出它的定义域;
(3)把△ABE沿着直线BE翻折,点A落在点 处,试探索:△ 能否为等腰三角形?如果能,请写出AE的长;如果不能,请说明理由。
(3)若在x,y轴上分别由两点P,Q,使得P,Q,B,C四点组成的四边形为平行四边形
3、如图,在正方形ABCD中,点P是射线BC上的任意一点(点B与点C除外),连接DP,分别过点C、A作直线DP的垂线,垂足为点E、F。
(1)当点P在BC的延长线上时,那么线段AF、CE、EF之间有怎样的数量关系?请证明你的结论;
6、菱形ABCD中,点E、F分别在BC、CD边上,且 。
(1)如果 =60°,求证:AE=AF;
(2)如果 ,(1)中的结论:AE=AF是否依然成立,请说明理由。
(3)如果AB长为5,菱形ABCD面积为20,设 ,求 关于 的函数解析式,并写出定义域。
7、如图,在正方形ABCD中,点E在边AB上(点E与点A、B不重合)。在点E作FG⊥DE,FG与边BC相交于点F,与边DA的延长线相交于点G。
初二压轴题(特殊的平行四边形)
————————————————————————————————作者:
————————————————————————————————日期:
初中数学备课组
教师
班级初二
学生
日期
上课时间
教学内容:压轴题综合
1、如图,四边形OABC与四边形ODEF都是正方形。
(1)当正方形ODEF绕点O在平面内旋转时,AD与CF有怎样的数量和位置关系?并证明你的结论;
