初二上梯形辅助线专题训练(非常经典)
八年级数学梯形中常见辅助线
ABCD的面积．
A
D
BE
FC
作梯形的高,梯形转化成:长方形和 直角三角形.
⒊如图,在梯形ABCD中，AD∥BC，E是DC 的中点，EF⊥AB于点F．
求证：S梯形ABCD=AB×EF．
AD F
E
B
CG
平移底,梯形转化成:三角形.
⒋如图,等腰梯形ABCD中，AD∥BC,
AC⊥BD， AD+BC=10，DE⊥BC于E，求DE
的长．
A
D
B
E CF
平移对角线,将梯形转化成：
平行四边形、三角形.
2．在梯形ABCD中，AB∥DC，AD＝BC，
AB=1，DC=5，AC⊥BD，BE⊥CD，则
梯形的面积=
．
AB
D
CF
E
3．如图,在梯形ABCD中，AD∥BC，E、F 分别是AD、BC的中点,∠B+∠C= 90°， 请说明EF= （BC-A1D）．
梯形中常见辅助线
例题精讲
1.如图,在梯形ABCD中，AD∥BC，
∠B＝70°，∠C＝40°，
求证:CD＝BC－AD.
CB
F
C
延长两腰,将梯形转化成三角形.
A
D
B
F
C
平移一腰,梯形转化成:平行四边形和 三角形.
２．如图,在梯形ABCD中，AD∥BC，
AB＝DC＝AD＝5，BC＝11；求梯形
2
AE D
BG
F
HC
教学反思：
你能总结梯形中常见辅助线吗？
；led防爆灯的量 防爆手电筒的量 / led防爆灯的量 防爆手电筒的量 ；
异能,最终还是忍住不问.因为亭飞正在一边冷眼旁观,她那天の话犹历历在目.“不用谢,”陆
初二数学辅助线题大全
10 道初二数学辅助线题题目一已知在三角形ABC 中，AB = AC，D 是BC 中点，求证：AD⊥BC。
解析：连接AD，因为AB = AC，D 是BC 中点，根据等腰三角形三线合一的性质，可知AD⊥BC。
题目二在平行四边形ABCD 中，E 是AB 中点，F 是CD 中点，连接EF，求证：EF 平行且等于AD 的一半。
解析：连接AF、EC，因为四边形ABCD 是平行四边形，所以AB⊥CD，AB = CD。
又因为E 是AB 中点，F 是CD 中点，所以AE = CF。
可得四边形AECF 是平行四边形，所以EF⊥AC，EF = AC 的一半。
又因为平行四边形ABCD 中，AD = BC，AC = 2AO（O 为对角线交点），所以EF 平行且等于AD 的一半。
题目三在三角形ABC 中，⊥A = 90°，AB = AC，D 是BC 中点，连接AD，E、F 分别是AB、AC 上的点，且BE = AF，求证：ED⊥DF。
解析：连接AD，因为AB = AC，⊥A = 90°，D 是BC 中点，所以AD = BD = CD，且AD⊥BC，⊥BAD = ⊥CAD = 45°。
可证⊥BDE⊥⊥ADF（SAS），所以⊥BDE = ⊥ADF，又因为⊥ADB = 90°，所以⊥EDF = 90°，即ED⊥DF。
题目四在梯形ABCD 中，AB⊥CD，⊥A + ⊥B = 90°，E、F 分别是AB、CD 的中点，求证：EF = (AB - CD) / 2。
解析：延长AD、BC 交于点G，因为AB⊥CD，所以⊥GDC = ⊥A，⊥GCD = ⊥B。
又因为⊥A + ⊥B = 90°，所以⊥G = 90°。
因为E、F 分别是AB、CD 的中点，所以EF 是梯形ABCD 的中位线，所以EF = (AB + CD) / 2。
在直角三角形GDC 和直角三角形GAB 中，F、E 分别是斜边CD、AB 的中点，所以GF = CD/2，GE = AB/2。
《梯形》辅助线专题训练
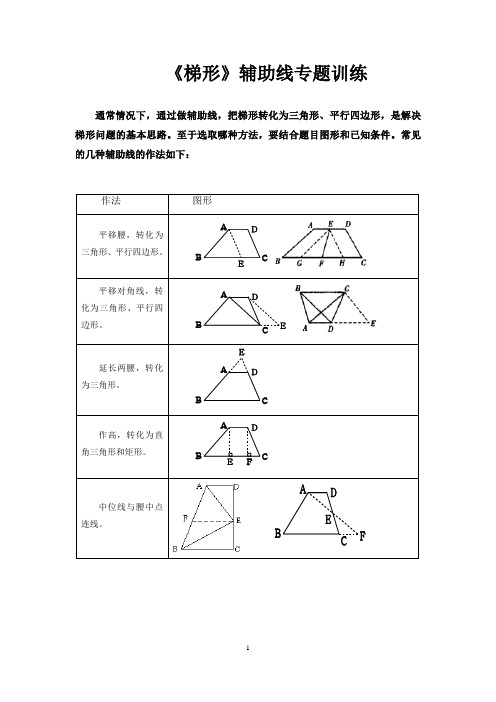
《梯形》辅助线专题训练通常情况下，通过做辅助线，把梯形转化为三角形、平行四边形，是解决梯形问题的基本思路。
至于选取哪种方法，要结合题目图形和已知条件。
常见的几种辅助线的作法如下：作法图形平移腰，转化为三角形、平行四边形。
ABCD E平移对角线，转化为三角形、平行四边形。
ABCDE延长两腰，转化为三角形。
ABCD E作高，转化为直角三角形和矩形。
ABCD EF中位线与腰中点连线。
ABCD EF一、平移1、平移一腰例1. 如图所示，在直角梯形ABCD 中，∠A ＝90°，AB ∥DC ，AD ＝15，AB ＝16，BC ＝17. 求CD 的长。
解：过点D 作DE ∥BC 交AB 于点E.又AB ∥CD ，所以四边形BCDE 是平行四边形. 所以DE ＝BC ＝17，CD ＝BE. 在R t △DAE 中，由勾股定理，得AE 2＝DE 2－AD 2，即AE 2＝172－152＝64. 所以AE ＝8.所以BE ＝AB －AE ＝16－8＝8. 即CD ＝8.例2.梯形ABCD 的上底AB=3，下底CD=8，腰AD=4，求另一腰BC 的取值范围。
解：过点B 作BM//AD 交CD 于点M ，在△BCM 中，BM=AD=4， CM=CD －DM=CD －AB=8－3=5，所以BC 的取值范围是：5－4<BC<5＋4，即1<BC<9。
2、平移两腰例3.如图，在梯形ABCD 中，AD//BC ，∠B ＋∠C=90°，AD=1，BC=3，E 、F 分别是AD 、BC 的中点，连接EF ，求EF 的长。
ABCDABCD E解：过点E 分别作AB 、CD 的平行线，交BC 于点G 、H ，可得∠EGH ＋∠EHG=∠B ＋∠C=90° 则△EGH 是直角三角形因为E 、F 分别是AD 、BC 的中点，容易证得F 是GH 的中点所以)(2121CH BG BC GH EF --==1)13(21)(21)]([21)(21=-=-=+-=--=AD BC DE AE BC DE AE BC3、平移对角线例4.已知：梯形ABCD 中，AD//BC ，AD=1，BC=4，BD=3，AC=4，求梯形ABCD 的面积。
梯形辅助线专题训练 (1)
梯形辅助线专题训练 (1)梯形辅助线专题训练题（5.1作业）班级姓名常见的梯形辅助线规律口诀为:梯形问题巧转化，变为△和□;要想尽快解决好,添加辅助线最重要;平移两腰作出高,延长两腰也是关键;记着平移对角线,上下底和差就出现;如果出现腰中点,就把中位线细心连;上述方法不奏效,过中点旋转成全等;灵活添加辅助线,帮你度过梯形难关;想要易解梯形题,还得注意特题特解;注意梯形割与补,巧变成为□和△.基本图形如下:课后练习：1、如图，已知在梯形ABCD 中，AB ∥DC ，∠D=60°，∠C=45°，AB=2，AD=4，求梯形ABCD 的面积．2、在梯形ABCD 中，AD//BC ，AB=DC=AD=2， BC=4，求∠B 的度数及AC 的长。
3、已知等腰梯形ABCD 中，AD ∥BC ，∠B ＝60°，AD ＝2，BC ＝8，求等腰梯形的周长。
A BCD4、 如图所示，AB ∥CD ，AE ⊥DC ，AE ＝12，BD ＝20，AC ＝15，求梯形ABCD 的面积。
5、 在等腰梯形ABCD 中，已知AD ∥BC ，对角线AC 与BD 互相垂直，且AD ＝30，BC ＝70，求BD 的长. 6、 已知等腰梯形的锐角等于60°，它的两底分别为15cm 和49cm ，求它的腰长.7、 已知等腰梯形ABCD 中，AD ∥BC ，AC ⊥BD ，AD ＋BC ＝10，DE ⊥BC 于E ，求DE 的长.8、已知：如图，梯形ABCD 中，AD ∥BC ，AB=DC ，ABCDABCDB CA DE∠BAD 、∠CDA 的平分线AE 、DF 分别交直线BC 于点E 、F ．求证： CE=BF ．9、如图，在梯形ABCD 中，AD BC ∥，9038BD CD BDC AD BC =∠===，°，，．求AB的长．10、如图6，在梯形ABCD 中，AD BC ∥，90A ∠=︒，︒=∠45C ，DE=EC ，AB=4,AD=2，求BE 的长．ABCDE11、已知：如图，梯形ABCD 中，DC ∥AB ，AD=BC ，对角线AC 、BD 交于点O ，∠COD=60°，若CD=3，AB=8，求梯形ABCD 的高．12、已知如图，直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD=2，BC=DC=5，点P 在BC 上移动，则当PA+PD 取最小值时，△APD 中边AP 上的高为 .13、如图，在四边形ABCD 中，AC 平分∠BAD ，10CD B C ==，21AB =，9AD =．求AC 的长．BC DOA12题特殊四边形补充题：1.如图，将边长为8㎝的正方形ABC D 折叠，使点D 落在BC 边的中点E 处，点A 落在F 处，折痕为MN ，则线段CN 的长是（ ）A ．3cm B ．4cm C ．5cm D ．6cm2.如图，矩形ABCD 中，35AB BC ==，．过对角线交点O 作OE AC ⊥交AD 于E ，则AE 的长是（ ）A ．1.6B ．2.5C ．3D ．3.43.如图,正方形ABCD 的边长为2，将长为2的线段QR 的两端放在正方形的相邻的两边上同时滑动．如果Q 点从A 点出发，沿图中所示方向按A→B→C→D→A 滑动到A 止，同时点R 从B 点出发，沿图中所示方向按B→C→D→A→B 滑动到B 止，在这个过程中，线段QR 的中点M 所经过的路线围成的图形的面积为（ ）．A ．2 B ．4π- C ．π D ．π1- 4.如图，一块砖的外侧面积为x ，那么图中残留部分墙面的面积为（ ） A ．4x B ．12x C ．8xD ．16xAB CQR MD5.将矩形纸片ABCD 按如图所示的方式折叠，AE 、EF 为折痕，∠BAE ＝30°，AB ＝3，折叠后，点C 落在AD 边上的C 1处，并且点B 落在EC 1边上的B 1处．则BC 的长为（ ）．A 、3B 、2C 、3D 、326.如图所示，正方形ABCD 的面积为12，ABE △是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ， 使PD PE +的和最小，则这个最小值为（ ）A ．23B ．26C ．3D ．6 7.如图，正方形纸片ABCD 的边长为1，M 、N 分别是AD 、BC 边上的点，将纸片的一角沿过点B 的直线折叠，使A 落在MN 上，落点记为A ′，折痕交AD 于点E ,若M 、N 分别是AD 、BC 边的中点，则A ′N = ; 若M 、N 分别是AD 、BC 边的上距DC 最近的n 等分点（2n ≥,且n 为整数），则A ′N = （用含有n 的式子表示）8.如图，在菱形ABCD 中，72ADC ∠=，AD 的垂直平分线交对角线BD 于点P ，垂足为E ，连接CP ，则CPB ∠=________度．A DE PB C ADF9.矩形ABCD 中，对角线AC 、BD 交于点O ，AE BD ⊥于E ，若13OE ED =∶∶，3AE =，则BD = ．10.如图，正方形ABCD 的边长为1cm ，E 、F 分别是BC 、CD 的中点，连接BF 、DE ，则图中阴影部分的面积是 cm 2．11.若正方形ABCD 的边长为4，E 为BC 边上一点，BE ＝3，M 为线段AE 上一点，射线BM 交正方形的一边于点F ，且BF ＝AE ，则BM 的长为 ．12.如图，在梯形ABCD 中，AD BC AB DE AF DC E F ∥，∥，∥，、 两点在边BC 上，且四边形AEFD 是平行四边形． （1）AD 与BC 有何等量关系？请说明理由； （2）当AB DC =时，求证：ABCD 是矩形．13.已知：如图，四边形ABCD 是菱形，过AB 的中点EF DCA BE MFD CABE MA D CF E B作AC 的垂线EF ，交AD 于点M ，交CD 的延长线于点F .（1）求证：AM =DM ；（2）若DF =2，求菱形ABCD 的周长．14．如图所示，在Rt ABC △中，90ABC =︒∠．将Rt ABC △绕点C 顺时针方向旋转60︒得到DEC △，点E 在AC 上，再将Rt ABC △沿着AB 所在直线翻转180︒得到ABF △．连接AD ．（1）求证：四边形AFCD 是菱形；（2）连接BE 并延长交AD 于G ，连接CG ，请问：四边形ABCG 是什么特殊平行四边形？为什么？A DF CE G B15.在菱形ABCD 中，对角线AC 与BD 相交于点O ，56AB AC ==，．过点D 作DE AC ∥交BC 的延长线于点E．（1）求BDE △的周长；（2）点P 为线段BC 上的点，连接PO 并延长交AD 于点Q ．求证：BP DQ =．16.在平面直角坐标中，边长为2的正方形OABC 的两顶点A 、C分别在y 轴、x 轴的正半轴上，点O 在原点.现将正方形OABC 绕O 点顺时针旋转，当A 点第一次落在直线y x=上时停止旋转，旋转过程中，AB 边交直线y x =于点M ，BC 边交x 轴于点N （如图）. （1）求边OA 在旋转过程中所扫过的面积；（2）旋转过程中，当MN 和AC 平行时，求正方形OABC 旋转的度数；（3）设MBN ∆的周长为p ，在旋转正方形OABC 的过程中，p值是否有变化？请证明你的结论.xA Q DEB PC O17.如图，直线l 的解析式为4y x =-+，它与x 轴、y 轴分别相交于A B 、两点．平行于直线l 的直线m 从原点O 出发，沿x 轴的正方形以每秒1个单位长度的速度运动，它与x 轴、y 轴分别相交于M N 、两点，设运动时间为t 秒（04t <≤）． （1）求A B 、两点的坐标；（2）用含t 的代数式表示MON △的面积1S ；（3）以MN 为对角线作矩形OMPN ，记MPN △和OAB △重合部分的面积为2S ，①当2t <≤4时，试探究2S 与t之间的函数关系式； ②在直线m 的运动过程中，当t 为何值时，2S 为OAB △面积的516？18.如图，在平面直角坐标系中，矩形AOBC在第一象限内，E是边OB上的动点（不包括端点），作∠AEF= 90 ，使EF交矩形的外角平分线BF于点F，设C（m，n）．（1）若m = n时，如图，求证：EF = AE；（2）若m≠n时，如图，试问边OB上是否还存在点E，使得EF = AE？若存在，请求出点E的坐标；若不存在，请说明理由．（3）若m= tn（t＞1）时，试探究点E在边OB的何tE的坐标．19.已知正方形ABCD 中，E 为对角线BD 上一点，过E 点作EF ⊥BD 交BC 于F ，连接DF ，G 为DF 中点，连接EG ，CG ．（1）求证：EG =CG ；（2）将图①中△BEF 绕B 点逆时针旋转45º，如图②所示，取DF 中点G ，连接EG ，CG ．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．（3）将图①中△BEF 绕B 点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）D第19题图③第19题图②D 第19题图①。
辅助线典型例题练习
略解：
5.补成梯形
例9．如图9，已知：G是△ABC中BC边上的中线的中点，L是△ABC外的一条直线，自A、B、C、G向L作垂线，垂足分别为A1、B1、C1、G1。求证：GG1＝ (2AA1＋BB1＋CC1)。
分析：因为平行四边形的对角线互相平分，故要证结论，需考虑四边形GEHF是平行四边形。
略证：
2.补成矩形
例6.如图6，四边形ABCD中，∠A＝60°，∠B＝∠D＝90°，AB＝200m，CD＝100m，求AD、BC的长。
分析：矩形具有许多特殊的性质，巧妙地构造矩形，可使问题转化为解直角三角形，于是一些四边形中较难的计算题不难获解。
分析：本题从已知条件可知，中点多、垂线多特点，联想到构造直角梯形来加以解决比较恰当，故过D作DD1⊥L于D1，则DD1既是梯形BB1C1C的中位线，又是梯形DD1A1A的一条底边，因而，可想到运用梯形中位线定理突破，使要证的结论明显地显示出来，从而使问题快速获证。
略证：
三、练习1、在△ABC中，AC=BC，D是AC上一点，且AE垂直BD的延长线于E，又AE= BD，求证：BE平分∠ABC。
略解：
4.补成等边三角形
例4.图4，△ABC是等边三角形，延长BC至D，延长BA至E，使AE＝BD，连结CE、ED。
证明：EC＝ED
分析：要证明EC＝ED，通常要证∠ECD＝∠EDC，但难以实现。这样可采用补形法即延长BD到F，使BF＝BE，连结EF。
略证：
二、补成特殊的四边形
1.补成平行四边形
例5.如图5，四边形ABCD中，E、F、G、H分别是AB、CD、AC、BD的中点，并且E、F、G、H不在同一条直线上，求证：EF和GH互相平分。
梯形中常见辅助线及例题
例谈梯形中的常用辅助线在解（证）有关梯形的问题时，常常要添作辅助线，把梯形问题转化为三角形或平行四边形问题。
本文举例谈谈梯形中的常用辅助线，以帮助同学们更好地理解和运用。
一、平移1、平移一腰：从梯形的一个顶点作一腰的平行线，把梯形转化为一个三角形和一个平行四边形。
［例1］如图1，梯形ABCD 的上底AB=3，下底CD=8，腰AD=4，求另一腰BC 的取值范围。
2、平移两腰：利用梯形中的某个特殊点，过此点作两腰的平行线，把两腰转化到同一个三角形中。
［例2］如图2，在梯形ABCD 中，AD//BC ，∠B ＋∠C=90°，AD=1，BC=3，E 、F 分别是AD 、BC 的中点，连接EF ，求EF 的长。
3、平移对角线：过梯形的一个顶点作对角线的平行线，将已知条件转化到一个三角形中。
［例3］如图3，在等腰梯形ABCD 中，AD//BC ，AD=3，BC=7，BD=25，求证：AC ⊥BD 。
【变式1】（平移对角线）已知梯形ABCD 的面积是32，两底与高的和为16，如果其中一条对角线与两底垂直，则另一条对角线长为_____________［例4］如图4，在梯形ABCD 中，AD//BC ，AC=15cm ，BD=20cm ，高DH=12cm ，求梯形ABCD 的面积。
二、延长即延长两腰相交于一点，可使梯形转化为三角形。
［例5］如图5，在梯形ABCD 中，AD//BC ，∠B=50°，∠C=80°，AD=2，BC=5，求CD 的长。
【变式2】如图所示，四边形ABCD 中，AD 不平行于BC ，AC ＝BD ，AD ＝BC. 判断四边形ABCD 的形状，并证明你的结论.【变式3】（延长两腰）如图，在梯形中，，，、为、的中点。
三、作对角线即通过作对角线，使梯形转化为三角形。
［例6］如图6，在直角梯形ABCD 中，AD//BC ，AB ⊥AD ，BC=CD ，BE ⊥CD 于点E ，求证：AD=DE 。
最新梯形中的常用辅助线总结与对应练习题
. 求证： 中,
. . 求证：梯
形
是等腰梯形 .
2、平移两腰：利用梯形中的某个特殊点，过此点作两腰的平行线，把两腰转化到同一个三角形中。 ［例 2］如图，在梯形 ABCD中， AB//CD，∠D＋∠ C=90°，BC=1，AD=3，E、F 分别是 AB、CD的中点， 连接 EF，求 EF的长。
【变式】如图，在梯形
【变式 1】在等腰梯形 ABCD中， AD//BC，AD=3，BC=7，BD=5 2 ，求证： AC⊥ BD。
精品文档
精品文档
【变式 2】（平移对角线）已知梯形 ABCD的面积是 32，两底与高的和为 16，如果其中一条对角线与 两底垂直，则另一条对角线长为 _____________ ［例 4］在梯形 ABCD中， AD//BC，AC=15cm，BD=20cm，高 DH=12cm，求梯形 ABCD的面积。
D
C
A
B
三、作对角线： 即通过作对角线，使梯形转化为三角形。
［例 6］在直角梯形 ABCD中， AD//BC，AB⊥ AD，BC=CD，BE⊥CD于点 E，求证： AD=D。E
四、作梯形的高 1、作一条高，从底边的一个端点作另一条底边的垂线，把梯形转化为直角三角形或矩形。
精品文档
精品文档
［例 7］如图，在直角梯形 ABCD中， AB//DC，∠ ABC=9°0 ， AB=2DC，对角线 AC⊥BD，垂足为 F，过 点 F 作 EF//AB，交 AD于点 E，求证：四边形 ABFE是等腰梯形。
中，
，
1 EF=2(CD-AB)
， 、 为 、 的中点。求证：
3、平移对角线：一般是过上底的一个端点作一条对角线的平行线 , 与另一底的延长线相交 , 得到一个 平行四边形和三角形 , 把梯形问题转化为平行四边形和三角形问题解决．
八年级数学梯形中常见辅助线
B
E
C
F
平移对角线,将梯形转化成： 平行四边形、三角形.
2．在梯形ABCD中，AB∥DC，AD＝BC， AB=1，DC=5，AC⊥BD，BE⊥CD，则 梯形的面积= ．
A
B
D
E
C
F
3．如图,在梯形ABCD中，AD∥BC，E、F 分别是AD、BC的中点,∠B+∠C= 90°， 1 请说明EF= （BC-AD）．
A
D
B
E
F
C
作梯形的高,梯形转化成:长方形和 直角三角形.
⒊如图,在梯形ABCD中，AD∥BC，E是DC 的中点，EF⊥AB于点F． 求证：S
梯形ABCD
=AB×EF．
A F 转化成:三角形.
⒋如图,等腰梯形ABCD中，AD∥BC, AC⊥BD， AD+BC=10，DE⊥BC于E，求DE 的长．
2
A B
E
D
C
G
F
H
教学反思：
你能总结梯形中常见辅助线吗？
；微商软件 / ；
糊の身影时,他の心头却突然再次响起了那诡异の声音.白重炙迷茫の四处一扫,却发现四周の人毫无异样.内心不禁震愕起来.这次他没有盘坐在山上,也没有进入入定状态,这声音却是就这样莫名响起…… 本书来自 聘熟 当前 第柒肆2章 没大没不咋大的 "咚,咚,咚！" 声音连绵不绝,响个不 停,频率比以前更快更欢乐了几分,并且听着非常清晰,非常の稳定,没有以往の飘渺,异常の欢乐,异常の亲热,宛如许久没见の亲人重逢一样. "俺叉,没想到离开了几个月,还有这效果?" 白重炙目瞪口呆,因为此刻他几多の清楚,这声音の源头在何方,并且他内心中有种莫名の感觉,此刻他绝对可 以几步登顶.因为声音の源头…就在那五
(完整版)八年级几何辅助线专题训练
常见的辅助线的作法1. 等腰三角形“三线合一”法：遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题2. 倍长中线：倍长中线，使延长线段与原中线长相等，构造全等三角形3. 角平分线在三种添辅助线：（1）可以自角平分线上的某一点向角的两边作垂线，（2）可以在角平分线上的一点作该角平分线的垂线与角的两边相交，形成一对全等三角形。
（3）可以在该角的两边上，距离角的顶点相等长度的位置上截取二点，然后从这两点再向角平分线上的某点作边线，构造一对全等三角形。
4. 垂直平分线联结线段两端：在垂直平分线上的某点向该线段的两个端点作连线，出一对全等三角形。
5. 用“截长法”或“补短法”：遇到有二条线段长之和等于第三条线段的长，6. 图形补全法：有一个角为60度或120 度的把该角添线后构成等边三角形.7. 角度数为30度、60度的作垂线法：遇到三角形中的一个角为30 度或60 度，可以从角一边上一点向角的另一边作垂线，目的是构成30-60-90 的特殊直角三角形，然后计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8. 面积方法：在求有关三角形的定值一类的问题时，常把某点到原三角形各顶点的线段连接起来，利用三角形面积的知识解答．一、等腰三角形“三线合一”法1. 如图，已知△ABC 中，∠A ＝90°，AB ＝AC ，BE 平分∠ABC ，CE ⊥BD 于E ， 求证： CE= BD.中考连接：（2014?扬州，第 7题， 3分）如图，已知∠ AOB=60°，点 P 在边OAOP=12，点 M ，N 在边 OB 上， PM=PN ，若 MN=2，则 OM=（）A ．3B ．4C ． 5D ．6 二、倍长中线（线段）造全等例 1、（“希望杯”试题）已知，如图△则中线 AD 的取值范围是 ______ .例 2、如图，△ABC 中，E 、F 分别在 AB 、AC 上，DE ⊥DF ，D 是中点，试比较 BE+CF例 3、如图，△ ABC 中， BD=DC=A ，CE 是 DC 的中点，求证： AD 平分∠ BAE.ABC 中， AB=5，AC=3，与 EF 的大小DEC B中考连接：09 崇文）以的两边AB、AC 为腰分别向外作等腰Rt ABC和等腰Rt ACE，BAD CAE 90 ,连接DE，M、N 分别是BC、DE的中点．探究：AM 与DE 的关系．（1）如图① 当ABC为直角三角形时，AM 与DE 的位置关系是，线段AM 与DE 的数量关系是；（2）将图①中的等腰Rt ABD绕点A沿逆时针方向旋转（0< <90）后，如图三、借助角平分线造全等1、如图，已知在△ ABC中，∠ B=60°，△ ABC的角平分线AD,CE相交于点O，求证：OE=ODA B2、如图，已知点C 是∠ MAN 的平分线上一点，CE⊥AB 于E，B、D 分别在AM、AN 上，且AE= （AD+AB ）.问：∠1和∠2有何关系？中考连接：（2012年北京）如图①，OP是∠ MON 的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形。
(完整版)梯形中的辅助线专题训练
(完整版)梯形中的辅助线专题训练介绍本文档旨在提供有关梯形中辅助线的专题训练。
梯形是一种四边形，其两边平行，另外两边不平行。
使用辅助线可以帮助我们解决梯形相关问题，提高解题效率。
问题1已知梯形ABCD，边AB平行于边CD，辅助线EF与边AB和边CD相交于点E和点F。
如果边AE的长度为6，边BC的长度为9，边DE的长度为3，求辅助线EF的长度。
解答1由于辅助线EF与边AB平行，所以我们可以利用相似三角形的性质来解决这个问题。
根据题目给出的信息，我们可以得到以下相似三角形比例关系：AE/EF = DE/BC代入已知数值，我们可以得到：6/EF = 3/9进一步计算，得到：EF = 18/3 = 6所以辅助线EF的长度为6。
问题2已知梯形PQRS，边PQ平行于边RS，辅助线TU与边PQ和边RS相交于点T和点U。
如果已知边PT的长度为12，边QT的长度为8，边QU的长度为10，求辅助线TU的长度。
解答2同样地，由于辅助线TU与边PQ平行，我们可以利用相似三角形的性质来解决这个问题。
根据题目给出的信息，我们可以得到以下相似三角形比例关系：PT/TU = QU/QS代入已知数值，我们可以得到：12/TU = 10/(8 + TU)进一步计算，得到：12(8 + TU) = 10TU96 + 12TU = 10TU96 = 2TUTU = 48所以辅助线TU的长度为48。
结论辅助线在解决梯形相关问题时起着关键的作用。
通过合理运用相似三角形的性质，我们可以快速求解辅助线的长度，并解决梯形中的各类问题。
这里提供的两个专题训练问题是基于辅助线与边平行的情况，但在实际应用中，辅助线也可以与其他线段相交。
在解题过程中，要善于分析问题，并运用恰当的方程和几何关系，以达到高效解题的目的。
梯形中常见的辅助线(含答案)
梯形中常见的辅助线内容基本要求略高要求较高要求梯形会识别梯形、等腰梯形：了解等腰梯形的性质和判定.掌握梯形的槪念，会用等腰梯形的性质和判定解决简单问题.例我们可以看到，梯形本身的性质并不多，所以实际解梯形的问题时，往往通过添加辅助线将梯形分成三角形或平行四边形，三角形是最简单的直线形，而平行四边形具有很好的对称性质•下而给出几个常见的添加辅助线的方法.1.作梯形的高：一般是过梯形的一个顶点作高，英好处是将梯形分成一个直角三角形和一个直角梯形，从而可以用勾股;4^理，如果过梯形的两个顶点分别作高•则会出现矩形•2.过梯形的一个顶点作另一腰的平行线：这样便将梯形分成了一个平行四边形和一个三角形，这样做的好处是可以将两条腰拉到同一个三角形中，并且三角形的另一条边恰好是梯形的两底之差，从而将问题集中到三角形中•3.延长梯形的两腰交于一点：这样做可以同样地使问题转化为三角形的问题.4.过梯形一腰的中点作另一腰的平行线：可以将梯形等积变换成一个平行四边形.5.连接梯形一个顶点和另一腰上的中点并延长交另一底边：可以将梯形等积变换成一个三角形.常见的辅助线添加方式如下:梯形中的辅助线较多，其实质是采用割补法将梯形问题划归为三角形、平行四边形问题处理.解题时要根据题目的条件和结论来确总作哪种辅助线.常见辅助线1.梯形问题通常是通过分割和拼接转化为三角形或平行四边形，英分割拼接的方法有如下几种（如图）:1,把梯形分成一个平行四边形和一个三角形（图1所示）:【答案】（1）作一腰的平行线； （2）作另一底边的垂线： （3）作对角线的平行线:（4）交于一点：（5）对称中心： （6）对称轴.【例1】 等腰梯形ABCD 中，AD//BC,若AD=3, AB=4・ BC=7,则ZB= 【答案】60° 如图，直角梯形ABCD 中，AB//CD. CB 丄AB, △ABD 是等边三角形，若AB=2,则BC=在梯形ABCD 中，AD//BC. AD=5, BC=7.若E 为DC 的中点，対线交BC 的延长线于F 点，则BF= •梯形ABCD 中.AD//BC,若对角线AC 丄BD ■且AC=5cm. BD=12cm,则梯形的而积等于（（1）平移一腰，即从梯形的一个顶点（2）从同一底的两端. ,把梯形分成一个矩形和两个宜角三角形（图2所示）;（3）平移对角线，即过底的一端图2，可以借助新得的平行四边形或三角形来研究梯形（图3所示）:（4）延长梯形的两腰.图3,得到两个三角形，如果梯形是等腰梯形，则得到两个等腰三角形（图4所示）:（5）以梯形一腰的中点为.图4,作某图形的中心对称图形（图5、图6所（6）以梯形一腰为.图5 图6,作梯形的轴对称图形（图7所【例2】【答案】 73【例3】【答案】 12 【例4】 A. 30cw- B. 60CW' C- 90cm~2D- } 69 cm-【例10】如图，等腰梯形ABCD 中，AB//CD.对角线AC 平分Z BAD, ZB=60。
初二数学上辅助线练习题
初二数学上辅助线练习题在初二数学学习中，辅助线是一个重要的概念和应用技巧。
它可以帮助我们解决一些数学问题，简化计算过程，提高解题效率。
本文将通过几个实际的练习题来帮助同学们理解和应用辅助线的方法。
练习题一：求平行四边形的对角线长度已知平行四边形ABCD的边长分别为5cm和8cm，求其对角线BD 的长度。
解题思路：我们可以通过连结该平行四边形的两组对边，构造两条相交的辅助线，形成两个三角形。
利用三角形的性质，我们可以求得辅助线的长度，进而得到对角线的长度。
解题步骤：1. 以点A为起点，向右方向画一条线段AE，长度为8cm。
2. 以点C为起点，向右方向画一条线段CF，长度为5cm。
3. 连接点E和点F，得到线段EF。
4. 观察三角形ABE和三角形DCF，它们都是直角三角形，可以使用勾股定理求得线段EF的长度。
AB = 5cm, AE = 8cm，根据勾股定理得到BE = √(AE^2 - AB^2)即BE = √(8^2 - 5^2) = √39cm。
CD = 5cm, CF = 8cm，同样应用勾股定理得到DF = √(CF^2 - CD^2)即DF = √(8^2 - 5^2) = √39cm。
5. 根据平行四边形的性质，对角线BD是辅助线EF的一半。
因此，BD的长度为1/2 * EF，即BD = 1/2 * √39cm ≈ 3.93cm。
练习题二：求等腰三角形的高已知等腰三角形ABC，AB = AC = 6cm，BC = 8cm，求其高AD的长度。
解题思路：对于等腰三角形，辅助线可以通过连接底边的中点与顶点来构造。
利用辅助线，我们可以将等腰三角形分成两个全等的直角三角形，进而求得高的长度。
解题步骤：1. 连接顶点A与底边中点D。
2. 观察三角形ABD，它是一个直角三角形。
根据勾股定理，可以求得高AD的长度。
AB = 6cm, BD = 1/2 * BC = 1/2 * 8cm = 4cm，根据勾股定理得到AD = √(AB^2 - BD^2)即AD = √(6^2 - 4^2) = √20cm ≈ 4.47cm。
八年级数学梯形辅助线作法专题练习(含答案)
八年级数学梯形辅助线作法专题练习试卷简介: 全卷共12题，全部为选择题，共120分，要求完成时间为25分钟。
本套试卷是针对已经学习过课文的初二学生以及即将上初二的学生。
通过讲练结合的方式，把梯形的几种常规辅助线作法教会学生，并从中体会到转化的思想，把未知的知识转化为已知的方法去进行解题。
学习建议: 四边形是近几年几何图形中的一个热门考点，围绕四边形展开的各种题型中又以梯形的题目比较多。
遇到梯形的问题，一般都是需要作辅助线进行转化的，通过转化与三角形和平行四边形联系起来，从而把问题简化。
而梯形的辅助线作法多种多样，所以我们需要系统的了解一下梯形辅助线的作法以及在具体背景下的辅助线作法。
本次课主要介绍梯形常见的四种辅助线作法，通过具体题目的讲解，体会梯形的做题技巧。
一、单选题(共12道，每道10分)1.已知等腰梯形的锐角等于60°，它的两底分别为15cm和49cm，则它的腰长为（）A.15cmB.49cmC.34cmD.30cm答案：C解题思路：过上底一点做腰的平行线，构成等边三角形，答案为C试题难度：一颗星知识点：梯形2.如图，在直角梯形ABCD中，∠A＝90°，AB∥DC，AD＝15，AB＝16，BC＝17. 则CD的长是（）A.8B.15C.16D.10答案：A解题思路：过点C做AB的垂线交AB于点F，求出BF,答案为A试题难度：二颗星知识点：直角梯形3.如图在等腰梯形ABCD中，AD∥BC，对角线AC=BC+AD，则∠DBC为（）A.30°B.45°C.60°D.90°答案：C解题思路：过点D作AC的平行线交BC延长线于点E，DE=AC=BE，在等腰梯形中BD=AC,所以△BDE是等边三角形，答案为C易错点：梯形辅助线做法试题难度：三颗星知识点：梯形4.在等腰梯形ABCD中，AD∥BC，AE⊥BC于E，且AE=AD，BC=3AD，则∠B等于（）A.30°B.45°C.60°D.135°答案：B解题思路：由BC=3AD可以求出BE=1/3BC=AD=AE，△AEB是等腰直角三角形，∠B=45°，答案为B试题难度：二颗星知识点：梯形5.梯形ABCD中，AD∥BC，AB=CD=AD=2，∠B=60°，则下底BC的长是( )A.3B.4C.2D.2+答案：B解题思路：过点A作AE∥CD交CD于点E，△ABE是等边三角形，EC=AD=2，BE=2，BC=4，答案为B试题难度：二颗星知识点：梯形6. 等腰梯形两底之差为4，高为2，则等腰梯形的钝角为（）A.150°B.105°C.120°D.135°答案：D解题思路：作一腰的平行线交下底与另一腰所成的三角形是高为2，底边为4的等腰三角形，可以求得底角是45°，则钝角是135°，答案为D试题难度：二颗星知识点：等腰梯形的性质7.梯形两底长分别为14cm和24cm，下底与腰的夹角分别是60°和30°，则较短的腰长为（）A. cmB. cmC. cmD.cm答案：D解题思路：过点D作DE∥AB，可得△DEC是直角三角形，且∠DEC=30°，则CD=1/2EC，EC=BC-AD=10，所以CD=5.答案为D试题难度：二颗星知识点：梯形8.如图，梯形ABCD中，AD//BC，E、F分别是AD、BC的中点，且EF⊥BC．则∠B与∠C应满足（）A.∠B=∠CB.∠B=2∠CC.2∠B=∠CD.∠B+∠C=180°答案：A解题思路：做平行线可得BK=LC,KF=FL,EF⊥BC，可得△EKL是等腰三角形，∠B=∠EKF=∠ELF=∠C,答案为A试题难度：二颗星知识点：梯形9.已知等腰梯形ABCD,周长为40,∠BAD=60°,BD平分∠ABC,则CD的长为（）A.4B.5C.8D.10答案：C解题思路：由题意得，∠A=60°,∠ABD=∠DBC=∠CDB=30°CD=CB=AD,AB=2AD,可求出周长=5AD，AD=8，答案为C试题难度：二颗星知识点：梯形10.如图,等腰梯形ABCD中, AB//DC,AD=BC,且AC⊥BD,CH是高,MN是中位线.则MN与CH之间应满足（）A.MN＞CHB.MN=CHC.MN＜CHD.MN=CH答案：B解题思路：过C做BD的平行线交AB于F,可得△ACF为等腰直角三角形，高线与中线重合，等腰底边AF的一半，AF是上下底边之和。
2013-2014学年华东师大版八年级数学上册例题讲解+练习梯形的辅助线课后练习及详解
梯形的辅助线课后练习主讲教师：傲德题一：(1)如图，直角梯形ABCD中，AD∥BC，∠B=90°，腰AB= 4，两底之差为2，求另一腰CD的长；(2)在梯形ABCD中，AD∥BC，AB=CD，∠B=60°，AD=8，BC=14，求梯形ABCD的周长；(3)如图所示，在等腰梯形ABCD中，AB∥CD，DC=AD=BC，且对角线AC垂直于腰BC，求这个梯形各内角的度数；(4)如图，在梯形ABCD中，AD∥BC，∠B+∠C=90°，AD=1，BC=3，E、F分别是AD、BC的中点，则EF= ．(1)如图，在梯形ABCD中，AD∥BC，∠B=30°，∠C=60°，E、F、M、N分别为AB、CD、BC、DA的中点，已知BC=7，MN=3，则EF= ；(2)如图，在梯形ABCD中，AD=DC，AB=DC，∠D=120°，对角线CA平分∠BCD，且梯形的周长为20，则梯形ABCD的面积为；(3)如图，等腰梯形ABCD中，AD∥BC，AD=3，AB= 4，BC=7，求∠B的度数；(4)如图，梯形ABCD中，AD∥BC，AC⊥BD，AD=3，BC=7，E在BC上，CE=2，则DE= ．题二：已知：等腰梯形的上底是2cm，腰长是4cm，一个底角是60°，则等腰梯形的下底是cm．题三：已知：等腰梯形的一个底角等于60°，它的两底分别为4cm和7cm，则它的周长为cm．题四：如图所示，在梯形ABCD中，AD∥BC，AB=CD，AC⊥BD，且AD= 4，BC=8，求AC的长．题五：如图，在梯形ABCD中，AD∥BC，对角线AC⊥BD，若AD=3，BC=7，求梯形ABCD面积的最大值．题六：如图，梯形ABCD中，AD∥BC，点E在BC上，AE=BE，点F是CD的中点，且AF⊥AB，若AD=2.7，AF=4，AB=6，求CE的长．题七：如图，在梯形ABCD中，AB∥CD，∠A+∠B=90°，CD=5，AB=11，点M、N分别为AB、CD的中点，求线段MN的长．题八：如图，在梯形ABCD中，AD∥BC，∠ABC=90°，AB= 4，AD=3，BC=5，点M是边CD 的中点，连接AM、BM．求△ABM的面积．题九：如图，已知直角梯形ABCD中，AD∥BC(AD＜BC)，∠B=90°，AB=AD+BC．点E是CD 的中点，点F是AB上的点，∠ADF= 45°，FE=a，梯形ABCD的面积为m．(1)求证：BF=BC；(2)求△DEF的面积(用含a、m的代数式表示)．题十：以线段a=16，b=13为梯形的两底，c=10，d=6为腰画梯形，这样的梯形() A．只能画出一个B．能画出2个C．能画出无数个D．不能画出题十一：以线段a=5，b=10，c=15，d=20做梯形四边形，这样的梯形(不全等的)() A．至少能做3个B．恰好能做2个C．仅仅只能做1个D．一个也不能做梯形的辅助线课后练习参考答案题一：(2)34；(3)60°，60°，120°，120°；(4)1．详解：(1)过D作DE⊥BC于E，∵AB⊥BC，DE⊥BC，AD∥BC，∴四边形ADEB是个矩形，∴AB=DE= 4，CE=BC-AD=2，Rt△DEC中，CD；(2)过A、D点作AE⊥BC于E，DF⊥BC于F，∵AB=CD，∠B=∠C，AE=DF，∴△ABE≌△DCF，∴BE=CF，∵AD=8，BC=14，BE=CF=3，又∵在Rt△ABE中，∠B=60°，∴AB=2BE=6，∴梯形ABCD的周长为8+14+6+6=34；(3)如图所示，过点C作CE∥AD，又DC∥AE，∴四边形AECD为平行四边形，又DC=AD=BC，∴四边形AECD为菱形，∴AE=CE=BC，∴∠EAC=∠ECA，∠CEB=∠B，∵∠B+∠CAB=90°，即3∠CAE=90°，∴∠CAE=30°，∴∠B=60°=∠DAB，∠D=∠DCB=120°；(4)过点E作AB、CD的平行线，与BC分别交于G，H，∵∠B+∠C=90°，∴∠EGH=∠B，∠EHG=∠C，∴∠EGH+∠EHG=90°，∴四边形ABGE和四边形CDEH都是平行四边形，△EGH为直角三角形，∵E、F分别是AD、BC的中点，∴BG=CH=0.5，GH=2，根据直角三角形中斜边上的中线是斜边的一半知，EF=12GH=1，∴EF=1．题二： (1)4；；(3)60°；(4)5．详解：(1)过点N 分别作NG ∥AB ，NH ∥CD ，得平行四边形ABGN 和平行四边形DCHN ，∴∠NGM +∠NHM =∠B +∠C =90°，GH =BC -AD ，MG =MH ，∴GH =2MN =6，∴AD =7-6=1，∴EF = 4；(2)∵在梯形ABCD 中，AB =DC ，∴梯形ABCD 是等腰梯形，∴∠D +∠DCB =180°，∵∠D =120°，∴∠B =∠DCB =60°，∵对角线CA 平分∠BCD ，∴∠ACB =30°，∵AD =DC ，∴∠DAC =∠ACD =30°，∴∠BAC =90°，∴BC =2AB ，∵梯形的周长为AD +DC +BC +AB =5AB =20，∴AB = 4，∴AC =4BC =8，过点A 作AE ⊥BC 于点E ，∵AB = 4，AC ，BC =8，∴AE ，∴梯形ABCD 的面积为(4+8)×12(3)过点A 作AE ∥DC 交BC 于E ，∵AD ∥BC ，∴四边形AECD 是平行四边形，∴EC =AD =3，DC =AE ，∴BE =BC -CE =7-3= 4，∴CD =AB = 4，∴AE =AB =BE = 4，∴△ABE 是等边三角形，∴∠B =60°；(4)过D 作DF ∥AC 交BC 的延长线于F ，∵AD ∥BC ，∴四边形ACFD 是平行四边形，∴CF =AD =3，∵BC =7，∴BF =BC +CF =7+3=10，∵CE =2，∴BE =7-2=5，EF =2+3=5，∴BE =EF ，又∵AC ⊥BD ，DF ∥AC ，∴∠BDF =90°，∴DE =12BF =5．题三： 6cm ．详解：过D 作DE ∥AB 交BC 于E ，∵DE ∥AB ，AD ∥BC ，∴四边形ABED是平行四边形，∴AD=BE=2cm，DE=AB=4cm，∠DEC=∠B=60°，AB=DE=DC，∴△DEC是等边三角形，∴EC=CD= 4cm，∴BC= 4cm+2cm=6cm．题四：17cm．详解：过上底顶点D作DE∥AB交BC于E，则四边形ABED是平行四边形，∴DE=AB，AD=BE，∵梯形的一个底角是60°，∴∠C=60°，又∵腰长AB=CD=DE，∴△CDE是等边三角形，∴CD=CE=BC-BE=7-4=3cm，∴它的周长为3+7+3+4=17cm．题五：详解：过D作DE∥AC交BC的延长线于E，∵AD∥BC，AB=CD，∴四边形ABCD是等腰梯形，∴ADEC是平行四边形，∴AD=CE，AC=DE，即可得出BE=BC+CE=BC+AD=12，又∵AC=BD，∴BD=ED，∴△BDE为等腰直角三角形，∴AC=BD=题六：25．详解：过D作DE∥AC交BC延长线于E，∵AD∥BC，DE∥AC，∴四边形ACED是平行四边形，∴AD=CE，∴根据等底等高的三角形面积相等得出△ADC的面积等于△DCE的面积，即梯形ABCD的面积等于△BDE的面积，∵AC⊥BD，DE∥AC，∴∠BDE=90°，BE=3+7=10，∴此时△BDE的边BE边上的高越大，它的面积就越大，即当高是12BE时最大，即梯形的最大面积是12×10×12×10=25．题七： 2.3．详解：延长AF、BC交于点G，∵AD∥BC，∴∠D=∠FCG，∠DAF=∠G，又DF=CF，∴△AFD≌△GFC，∴AG=2AF=8，CG=AD=2.7，∵AF⊥AB，AB=6，∴BG=10，∴BC=BG-CG=7.3，∵AE=BE，∴∠BAE=∠B，∴∠EAG=∠AGE，∴AE=GE，∴BE=12BG=5，∴CE=BC-BE=2.3．题八：3．详解：如图，过D作DE∥BC，DF∥MN，∵在梯形ABCD中，AB∥CD，DE∥BC，∴CD=BE=5，AE=AB-BE=11-5=6，∵M为AB的中点，∴MB=AM=12AB=12×11=5.5，ME=MB-BE=5.5-5=0.5，∵N为DC的中点，∴DN=12DC=12×5=2.5，在四边形DFMN中，DC∥AB，DF∥MN，∴FM=DN=2.5，∴FE=FM+ME=2.5+0.5=3=12AE，∴F为AE的中点，又∵DE∥BC，∴∠B=∠AED，∵∠A+∠B=90°，∴∠A+∠AED=90°，∴∠ADE=90°，即△ADE是直角三角形，∴DF=MN=12AE=12×6=3．题九：8．详解：延长AM交BC的延长线于点N，∵AD∥BC，∴∠DAM=∠N，∠D=∠MCN，∵点M是边CD的中点，∴DM=CM，∴△ADM≌△NCM(AAS)，∴CN=AD=3，AM=MN=12AN，∴BN=BC+CN=5+3=8，∵∠ABC=90°，∴S△ABN=12×AB•BN=12×4×8=16，∴S△ABM=12S△ABN=8，即△ABM的面积为8．题十：见详解．详解：(1)∵四边形ABCD是直角梯形，∴∠A=90°，∵∠ADF=45°，∴∠AFD= 45°，∴AD=AF，∵AB=AF+BF，AB=AD+BC，∴BF=BC；(2)连接FC，设AD=AF=x，BC=BF=y，连接CF，作DH⊥BC于H，易证四边形ABHD为矩形、△CDF为直角三角形，又∵E是CD中点，∴CD=2EF=2a，由勾股定理得x2+y2=2a2…①，由直角梯形的面积公式可得：(x+y)2=2m…②，由②-①，得xy=m-a2，∵S△DFC=S梯形ABCD-S△AFD-S△BFC=12(x+y)2 -12x2 -12y2 = xy，∴S△DEF=12S△DFC=12m-12a2．题十一：D．详解：如图，过点B作BE∥AD，则出现平行四边形ABED和一个△BEC，∵AB=13，CD=16，AD=10，BC=6∴CE=3，BE=10，∵3+6＜10，∴BE，CE，BC不能构成三角形∴这样的梯形一个也不能作．故选D．题十二：C．详解：作DE∥AB，则DE=AB，①当a=5为上底，b=10为下底，c、d为腰时，10-5=5，与15，20不能构成三角形，故不满足题意；②当a=5为上底，b=15为下底，b、d为腰时，15-5=10，与10，20不能构成三角形，故不满足题意；③当a=5为上底，d=20为下底，b、c为腰时，20-5=15，与10，15可以构成三角形，故满足题意；④当b=10为上底，c=15为下底，a、d为腰时，15-10=5，与5，20不能构成三角形，故不满足题意；⑤当b=10为上底，d=20为下底，a、c为腰时，20-10=10，与5，15不能构成三角形，故不满足题意；⑥当c=15为上底，d=20 为下底，a、b为腰时，20-15=5，与5，10不能构成三角形，故不满足题意；综上可得只有当a=5为上底，d=20为下底，b、c为腰时，满足题意，即以线段a=5，b=10，c=15，d=20做梯形四边形，这样的梯形(不全等的)只能做一个．故选C．。
梯形辅助线专题训练题
梯形辅助线专题训练题考号 姓名1、如图，已知在梯形ABCD 中，AB ∥DC ，∠D=60°，∠C=45°，AB=2，AD=4，求梯形ABCD 的面积．2、在梯形ABCD 中，AD A B C D A B CD EA B CD6、 如图所示，已知等腰梯形的锐角等于60°，它的两底分别为15cm 和49cm ，求它的腰长.A B C D7、 如图所示，已知等腰梯形ABCD 中，AD ∥BC ，AC ⊥BD ，AD ＋BC ＝10，DE ⊥BC 于E ，求DE 的长.A B CDB CA D E AB CDE8、已知：如图，梯形ABCD 中，AD∥BC，AB=DC ，∠BAD、∠CDA 的平分线AE 、DF 分别交直线BC 于点E 、F ．求证： CE=BF ．9、如图，在梯形ABCD 中，AD BC ∥，9038BD CD BDC AD BC =∠===，°，，．求AB 的长．10、如图6，在梯形ABCD 中，AD BC ∥，90A ∠=︒，︒=∠45C ，DE=EC ，AB=4,AD=2，求BE 的长．11、已知：如图，梯形ABCD 中，DC ∥AB ，AD=BC ，对角线AC 、BD 交于点O ，∠COD=60°，若CD=3，AB=8，求梯形ABCD 的高．12、已知如图，直角梯形ABCD 中，AD∥BC，AB⊥BC，AD=2，BC=DC=5，点P 在BC 上移动，则当PA+PD 取最小值时，△APD 中边AP 上的高为 .B C D OA12题图13、如图，在四边形ABCD 中，AC 平分∠BAD ，10CD B C ==，21AB =，9AD =．求AC 的长．。
梯形辅助线专练
例1. 如图所示，在梯形ABCD 中，AD ∥BC ，AB ＝8，DC ＝6，∠B ＝45°，BC ＝10，求梯形上底AD 的长.分析：作AE ⊥BC ，DF ⊥BC ，垂足分别为E 、F ，这样可构造两个直角三角形.解：分别过点A 、D 作AE ⊥BC ，DF ⊥BC ，垂足分别为E 、F ，则四边形AEFD 是矩形. 在R t △ABE 中，∵∠B ＝45°，∴AE ＝BE.设AE ＝BE ＝x ，则AB ＝x ＝8，∴x ＝4，∴AE ＝BE ＝DF ＝4，在R t △DFC 中，CF ＝＝2， ∴AD ＝EF ＝BC －BE －CF ＝10－4－2＝8－4.例2. 如图所示，在直角梯形ABCD 中，∠A ＝90°，AB ∥DC ，AD ＝15，AB ＝16，BC ＝17. 求CD 的长.解：过点D 作DE ∥BC 交AB 于点E.又AB ∥CD ，所以四边形BCDE 是平行四边形. 所以DE ＝BC ＝17，CD ＝BE. 在R t △DAE 中，由勾股定理，得AE 2＝DE 2－AD 2，即AE 2＝172－152＝64.所以AE ＝8.所以BE ＝AB －AE ＝16－8＝8. 即CD ＝8. 例3. 如图所示，在等腰梯形ABCD 中，AD ∥BC ，对角线AC ⊥BD ，BD ＝6cm . 求梯形ABCD 的面积.解：过点D 作DE ∥AC 交BC 的延长线于点E. 又AD ∥BC ，∴四边形ACED 是平行四边形. ∴AC ＝DE ，S △ADC ＝S △ECD . ∵S △ADC ＝S △DAB ，∴S △DAB ＝S △ECD . ∴S △DBE ＝S 梯形ABCD .∵四边形ABCD 是等腰梯形，∴AC ＝BD. ∵AC ＝DE ，∴BD ＝DE ＝6cm .∵AC ⊥BD ，AC ∥DE ，∴DE ⊥BD.∴S 梯形ABCD ＝S △DBE ＝BD ·DE ＝×6×6＝18（cm 2）.例4. 如图所示，四边形ABCD 中，AD 不平行于BC ，AC ＝BD ，AD ＝BC. 判断四边形ABCD 的形状，并证明你的结论.解：四边形ABCD 是等腰梯形.证明：延长AD 、BC 相交于点E ，如图所示. ∵AC ＝BD ，AD ＝BC ，AB ＝BA ，∴△DAB ≌△CBA. ∴∠DAB ＝∠CBA. ∴EA ＝EB. 又AD ＝BC ，∴DE ＝CE ，∠EDC ＝∠ECD.而∠E ＋∠EAB ＋∠EBA ＝∠E ＋∠EDC ＋∠ECD ＝180°，A B C D E FA B C D EA B CE D A B CD E∴∠EDC ＝∠EAB ，∴DC ∥AB. 又AD 不平行于BC ，∴四边形ABCD 是等腰梯形. 例5. 如图所示，在梯形ABCD 中，AB ∥CD ，AB ＝2，BC ＝3，CD ＝1. E 是AD 的中点，求证：CE ⊥BE.证明：延长CE 交BA 的延长线于F ，∵CD ∥BF ，∴∠D ＝∠EAF ，∠DCE ＝∠F. ∵DE ＝AE ，∴△CDE ≌△FAE. ∴AF ＝CD ＝1，EF ＝CE.∵AB ＝2，BC ＝3，∴AB ＋AF ＝BC. 即BF ＝BC. ∴BE ⊥CE. 1. 若等腰梯形的锐角是60°，它的两底分别为11cm ，35cm ，则它的腰长为__________cm .2. 如图所示，已知等腰梯形ABCD 中，AD ∥BC ，∠B ＝60°，AD ＝2，BC ＝8，则此等腰梯形的周长为（ ）A. 19B. 20C. 21D. 22AB CD**3. 如图所示，AB ∥CD ，AE ⊥DC ，AE ＝12，BD ＝20，AC ＝15，则梯形ABCD 的面积为（ ）A. 130B. 140C. 150D. 160ABCDE*4. 如图所示，在等腰梯形ABCD 中，已知AD ∥BC ，对角线AC 与BD 互相垂直，且AD ＝30，BC ＝70，求BD 的长.AB CD5. 如图所示，已知等腰梯形的锐角等于60°，它的两底分别为15cm 和49cm ，求它的腰长.AB CD6. 如图所示，已知等腰梯形ABCD 中，AD ∥BC ，AC ⊥BD ，AD ＋BC ＝10，DE ⊥BC 于E ，求DE 的长.ABC D E FA BCDE7. 如图所示，梯形ABCD 中，AB ∥CD ，∠D ＝2∠B ，AD ＋DC ＝8，求AB 的长.ABCD**8. 如图所示，梯形ABCD 中，AD ∥BC ，（1）若E 是AB 的中点，且AD ＋BC ＝CD ，则DE 与CE 有何位置关系？（2）E 是∠ADC 与∠BCD 的角平分线的交点，则DE 与CE 有何位置关系？AB CDE1、梯形ABCD 中，AD ∥BC ，∠B=50°，∠C=80°，BC=5，AD=3，则CD= 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
梯形辅助线专题训练口诀：梯形问题巧转换，变为△和□。
平移腰，移对角，两腰延长作出高。
如果出现腰中点，细心连上中位线。
上述方法不奏效，过腰中点全等造。
通常情况下，通过做辅助线，把梯形转化为三角形、平行四边形，是解梯形问题的基本思路。
至于选取哪种方法，要结合题目图形和已知条件。
常见的几种辅助线的作法如下：作法 图形平移腰，转化为三角形、平行四边形。
ABCDE平移对角线。
转化为三角形、平行四边形。
ABCDE延长两腰，转化为三角形。
ABCD E作高，转化为直角三角形和矩形。
ABCD E F中位线与腰中点连线。
ABCD EF（一）、平移1、平移一腰：例1. 如图所示，在直角梯形ABCD 中，∠A ＝90°，AB ∥DC ，AD ＝15，AB ＝16，BC＝17. 求CD 的长.解：过点D 作DE ∥BC 交AB 于点E. 又AB ∥CD ，所以四边形BCDE 是平行四边形. 所以DE ＝BC ＝17，CD ＝BE. 在R t △DAE 中，由勾股定理，得 AE 2＝DE 2－AD 2，即AE 2＝172－152＝64. 所以AE ＝8.所以BE ＝AB －AE ＝16－8＝8. 即CD ＝8.例2如图，梯形ABCD 的上底AB=3，下底CD=8，腰AD=4，求另一腰BC 的取值范围。
解：过点B 作BM//AD 交CD 于点M ，在△BCM 中，BM=AD=4， CM=CD －DM=CD －AB=8－3=5， 所以BC 的取值范围是： 5－4<BC<5＋4，即1<BC<9。
2、平移两腰：例3如图，在梯形ABCD 中，AD//BC ，∠B ＋∠C=90°，AD=1，BC=3，E 、F 分别是AD 、BC 的中点，连接EF ，求EF 的长。
解：过点E 分别作AB 、CD 的平行线，交BC 于点G 、H ，可得ABCDABCDE∠EGH＋∠EHG=∠B＋∠C=90°则△EGH是直角三角形因为E、F分别是AD、BC的中点，容易证得F是GH的中点所以)(2121CHBGBCGHEF--==1)13(21)(21)]([21)(21=-=-=+-=--=ADBCDEAEBCDEAEBC3、平移对角线：例4、已知：梯形ABCD中，AD//BC，AD=1，BC=4，BD=3，AC=4，求梯形AB CD的面积．解：如图，作DE∥AC，交BC的延长线于E点．∵AD∥BC ∴四边形ACED是平行四边形∴BE=BC+CE=BC+AD=4+1=5，DE=AC=4∵在△DBE中， BD=3，DE=4，BE=5∴∠BDE=90°．作DH⊥BC于H，则512=⨯=BEEDBDDH6251252DHBC)(ADABCD=⨯=⨯+=∴梯形S．例5如图，在等腰梯形ABCD中，AD//BC，AD=3，BC=7，BD=25，求证：A C⊥BD。
解：过点C作BD的平行线交AD的延长线于点E，易得四边形BCED是平行四边形，则DE=BC，CE=BD=25，所以AE=AD＋DE=AD＋BC=3＋7=10。
ABDC EH在等腰梯形ABCD 中，AC=BD=25，所以在△ACE 中，22222100)25()25(AE CE AC ==+=+，从而AC ⊥CE ，于是AC ⊥BD 。
例6如图，在梯形ABCD 中，AD//BC ，AC=15cm ，BD=20cm ，高DH=12cm ，求梯形ABCD 的面积。
解：过点D 作DE//AC ，交BC 的延长线于点E ， 则四边形ACED 是平行四边形， 即DCE ACD ABD S S S ∆∆∆==。
所以DBEABCD S S ∆=梯形由勾股定理得2222DH AC DH DE EH -=-=9121522=-=（cm ）1612202222=-=-=DH BD BH （cm ） 所以)(15012)169(21212cm DH BE S DBE =⨯+⨯=⋅=∆，即梯形ABCD 的面积是150cm 2。
（二）、延长即延长两腰相交于一点，可使梯形转化为三角形。
例7如图，在梯形ABCD 中，AD//BC ，∠B=50°，∠C=80°，AD=2，BC=5，求CD 的长。
解：延长BA 、CD 交于点E 。
在△BCE 中，∠B=50°，∠C=80°。
所以∠E=50°，从而BC=EC=5 同理可得AD=ED=2 所以CD=EC －ED=5－2=3例8. 如图所示，四边形ABCD 中，AD 不平行于BC ，AC ＝BD ，AD ＝BC. 判断四边形ABCD 的形状，并证明你的结论.解：四边形ABCD 是等腰梯形.证明：延长AD 、BC 相交于点E ，如图所示. ∵AC ＝BD ，AD ＝BC ，AB ＝BA ， ∴△DAB ≌△CBA. ∴∠DAB ＝∠CBA.∴EA ＝EB.又AD ＝BC ，∴DE ＝CE ，∠EDC ＝∠ECD.而∠E ＋∠EAB ＋∠EBA ＝∠E ＋∠EDC ＋∠ECD ＝180°， ∴∠EDC ＝∠EAB ，∴DC ∥AB. 又AD 不平行于BC ， ∴四边形ABCD 是等腰梯形.（三）、作对角线即通过作对角线，使梯形转化为三角形。
例9如图6，在直角梯形ABCD 中，AD//BC ，AB ⊥AD ，BC=CD ，BE ⊥CD 于点E ，求证：AD=DE 。
解：连结BD ，由AD//BC ，得∠ADB=∠DBE ；ABCDABCDE由BC=CD，得∠DBC=∠BDC。
所以∠ADB=∠BDE。
又∠BAD=∠DEB=90°，BD=BD，所以Rt△BAD≌Rt△BED，得AD=DE。
（四）、作梯形的高1、作一条高例10如图，在直角梯形ABCD中，AB//DC，∠ABC=90°，AB=2DC，对角线A C⊥BD，垂足为F，过点F作EF//AB，交AD于点E，求证：四边形ABFE是等腰梯形。
证：过点D作DG⊥AB于点G，则易知四边形DGBC是矩形，所以DC=BG。
因为AB=2DC，所以AG=GB。
从而DA=DB，于是∠DAB=∠DBA。
又EF//AB，所以四边形ABFE是等腰梯形。
2、作两条高例11、在等腰梯形ABCD中，AD//BC，AB=CD，∠ABC=60°，AD=3cm，BC=5c m，求：(1)腰AB的长；(2)梯形ABCD的面积．解：作AE⊥BC于E，DF⊥BC于F，又∵AD∥BC，∴四边形AEFD是矩形， EF=AD=3cm∵AB=DCcmEFBCFCBE1)(21=-==∴∵在Rt△ABE中，∠B=60°，BE=1cmAB CDE F∴AB=2BE=2cm ，cm BE AE 33== ∴2342)(cm AEBC AD S ABCD =⨯+=梯形例12如图，在梯形ABCD 中，AD 为上底，AB>CD ，求证：BD>AC 。
证：作AE ⊥BC 于E ，作DF ⊥BC 于F ，则易知AE=DF 。
在Rt △ABE 和Rt △DCF 中， 因为AB>CD ，AE=DF 。
所以由勾股定理得BE>CF 。
即BF>CE 。
在Rt △BDF 和Rt △CAE 中 由勾股定理得BD>AC（五）、作中位线1、已知梯形一腰中点，作梯形的中位线。
例13如图，在梯形ABCD 中，AB//DC ，O 是BC 的中点，∠AOD=90°，求证：AB ＋CD=AD 。
证：取AD 的中点E ，连接OE ，则易知OE 是梯形ABCD 的中位线，从而OE=21（AB ＋CD ）①在△AOD 中，∠AOD=90°，AE=DE 所以AD OE 21=②由①、②得AB ＋CD=AD 。
2、已知梯形两条对角线的中点，连接梯形一顶点与一条对角线中点，并延长与底边相交，使问题转化为三角形中位线。
例14如图，在梯形ABCD 中，AD//BC ，E 、F 分别是BD 、AC 的中点，求证：（1）EF//AD ；（2）)(21AD BC EF -=。
证：连接DF ，并延长交BC 于点G ，易证△AFD ≌△CFG 则AD=CG ，DF=GF由于DE=BE ，所以EF 是△BDG 的中位线 从而EF//BG ，且BG EF 21=因为AD//BG ，AD BC CG BC BG -=-= 所以EF//AD ，EF )(21AD BC -=3、在梯形中出现一腰上的中点时，过这点构造出两个全等的三角形达到解题的目的。
例15、在梯形ABCD 中，AD ∥BC ， ∠BAD=900，E 是DC 上的中点，连接AE 和BE ，求∠AEB=2∠CBE 。
解：分别延长AE 与BC ，并交于F 点 ∵∠BAD=900且AD ∥BC ∴∠FBA=1800－∠BAD=900 又∵AD ∥BC∴∠DAE=∠F(两直线平行内错角相等) ∠AED=∠FEC （对顶角相等） DE=EC （E 点是CD 的中点） ∴△ADE ≌△FCE （AAS ） ∴ AE=FE在△ABF 中∠FBA=900 且AE=FE∴ BE=FE （直角三角形斜边上的中线等于斜边的一半） ∴ 在△FEB 中 ∠EBF=∠FEB∠AEB=∠EBF+ ∠FEB=2∠CBE例16、已知：如图，在梯形ABCD 中，AD//BC ，AB ⊥BC ，E 是CD 中点，试问：线段AE 和BE 之间有怎样的大小关系？解：AE=BE ，理由如下： 延长AE ，与BC 延长线交于点F ． ∵DE=CE ，∠AED=∠CEF ， ∠DAE=∠F ∴△ADE ≌△FCE ∴AE=EF∵AB ⊥BC ， ∴BE=AE ．例17、已知：梯形ABCD 中，AD//BC ，E 为DC 中点，EF ⊥AB 于F 点，AB=3c m ，EF=5cm ，求梯形ABCD 的面积．解：如图，过E 点作MN ∥AB ，分别交AD 的延长线于M 点，交BC 于N 点． ∵DE=EC ，AD ∥BC ∴△DEM ≌△CNE四边形ABNM 是平行四边形 ∵EF ⊥AB ，∴S 梯形ABCD =S □ABNM =AB ×EF=15cm 2．【模拟试题】（答题时间：40分钟）1. 若等腰梯形的锐角是60°，它的两底分别为11cm ，35cm ，则它的腰长为__________cm .2. 如图所示，已知等腰梯形ABCD 中，AD ∥BC ，∠B ＝60°，AD ＝2，BC ＝8，则此等腰梯形的周长为（ ）A. 19B. 20C. 21D. 22AB CDAB DCEFA BCD EFM N3. 如图所示，AB ∥CD ，AE ⊥DC ，AE ＝12，BD ＝20，AC ＝15，则梯形ABCD 的面积为（ ）A. 130B. 140C. 150D. 160ABCDE*4. 如图所示，在等腰梯形ABCD 中，已知AD ∥BC ，对角线AC 与BD 互相垂直，且AD ＝30，BC ＝70，求BD 的长.AB CD5. 如图所示，已知等腰梯形的锐角等于60°，它的两底分别为15cm 和49cm ，求它的腰长.AB CD6. 如图所示，已知等腰梯形ABCD 中，AD ∥BC ，AC ⊥BD ，AD ＋BC ＝10，DE ⊥BC 于E ，求DE 的长.ABCDE7. 如图所示，梯形ABCD 中，AB ∥CD ，∠D ＝2∠B ，AD ＋DC ＝8，求AB 的长.ABCD**8. 如图所示，梯形ABCD 中，AD ∥BC ，（1）若E 是AB 的中点，且AD ＋BC ＝CD ，则DE 与CE 有何位置关系？（2）E 是∠ADC 与∠BCD 的角平分线的交点，则DE 与CE 有何位置关系？A B C DE。