黄立宗推荐-梯形辅助线专题训练题--好
【黄冈中考】备战中考数学 梯形的押轴题解析汇编二 人教新课标版
【黄冈中考】备战2012年中考数学—— 梯形的押轴题解析汇编二梯形一、选择题1.（2011湖南长沙，10，3分）如图，等腰梯形ABCD 中，AD ∥BC ，∠B =45°，AD =2，BC =4，则梯形的面积为（ ） A.3 B.4C.6D.8【解题思路】根据梯形的面积公式计算，该等腰梯形的高未知.通过添加高线将四边形问题转化为三角形问题，通过解直角三角形求出高的长度，进而求出梯形面积.【答案】解：过点A 作AM ⊥BC 于M ，过点B 作DN ⊥BC 于N ，于是四边形AMND 为矩形，所以MN=AD=2，Rt △ABM ≌△DCN ，所以BM=CN=（4-2）÷2=1.因为∠B =45°，所以在Rt △ ABM中，AM=BM=1.因此梯形的面积为：=+AM BC AD )(211)42(21⨯+=3. 故选A.【点评】本题考查了梯形的性质及面积计算.关于梯形问题是中考的一考查点之一.往往需要作辅助线，将其转化为矩形或三角形问题.这样问题一般难度中等.1. （2011台北28）某直角柱的两底面为全等的梯形，其四个侧面的面积依序为20平方公 分、36平方公分、20平方公分、60平方公分，且此直角柱的高为4公分。
求此直角柱的体 积为多少立方公分？(A) 136 (B) 192 (C) 240 (D) 544【分析】：由四个侧面的面积可判定两个底面是等腰梯形，两底长分别是9、15；腰长是5。
做出等腰梯形的高，根据勾股定理易求的高是4，在计算出面积. 【答案】：B【点评】：快速判定底面是等腰梯形是解题的关键，进而做出梯形的两个高，运用勾股定理 求出梯形的高，代人公式即可。
难度中等. 3. （2011年湖北省武汉市，7，3分）如图，在梯形ABCD 中，AB ∥DC ，AD=DC=CB ，若∠ABD ＝25°，则∠BAD 的大小是A.40°.B.45°.C.50°.D.60°.分析：由AB ∥DC ，可得∠BDC=∠ABD=25°，DC=CB ，可得∠BDC=∠CBD=25°，所以∠ABC=50°.利用等腰梯形两个底角相等. 答案：C点评：本题是一道难度较大的题。
梯形辅助线专练
例1. 如图所示，在梯形ABCD 中，AD ∥BC ，AB ＝8，DC ＝6，∠B ＝45°，BC ＝10，求梯形上底AD 的长.分析：作AE ⊥BC ，DF ⊥BC ，垂足分别为E 、F ，这样可构造两个直角三角形.解：分别过点A 、D 作AE ⊥BC ，DF ⊥BC ，垂足分别为E 、F ，则四边形AEFD 是矩形. 在R t △ABE 中，∵∠B ＝45°，∴AE ＝BE.设AE ＝BE ＝x ，则AB ＝x ＝8，∴x ＝4，∴AE ＝BE ＝DF ＝4，在R t △DFC 中，CF ＝＝2， ∴AD ＝EF ＝BC －BE －CF ＝10－4－2＝8－4.例2. 如图所示，在直角梯形ABCD 中，∠A ＝90°，AB ∥DC ，AD ＝15，AB ＝16，BC ＝17. 求CD 的长.解：过点D 作DE ∥BC 交AB 于点E.又AB ∥CD ，所以四边形BCDE 是平行四边形. 所以DE ＝BC ＝17，CD ＝BE. 在R t △DAE 中，由勾股定理，得AE 2＝DE 2－AD 2，即AE 2＝172－152＝64.所以AE ＝8.所以BE ＝AB －AE ＝16－8＝8. 即CD ＝8. 例3. 如图所示，在等腰梯形ABCD 中，AD ∥BC ，对角线AC ⊥BD ，BD ＝6cm . 求梯形ABCD 的面积.解：过点D 作DE ∥AC 交BC 的延长线于点E. 又AD ∥BC ，∴四边形ACED 是平行四边形. ∴AC ＝DE ，S △ADC ＝S △ECD . ∵S △ADC ＝S △DAB ，∴S △DAB ＝S △ECD . ∴S △DBE ＝S 梯形ABCD .∵四边形ABCD 是等腰梯形，∴AC ＝BD. ∵AC ＝DE ，∴BD ＝DE ＝6cm .∵AC ⊥BD ，AC ∥DE ，∴DE ⊥BD.∴S 梯形ABCD ＝S △DBE ＝BD ·DE ＝×6×6＝18（cm 2）.例4. 如图所示，四边形ABCD 中，AD 不平行于BC ，AC ＝BD ，AD ＝BC. 判断四边形ABCD 的形状，并证明你的结论.解：四边形ABCD 是等腰梯形.证明：延长AD 、BC 相交于点E ，如图所示. ∵AC ＝BD ，AD ＝BC ，AB ＝BA ，∴△DAB ≌△CBA. ∴∠DAB ＝∠CBA. ∴EA ＝EB. 又AD ＝BC ，∴DE ＝CE ，∠EDC ＝∠ECD.而∠E ＋∠EAB ＋∠EBA ＝∠E ＋∠EDC ＋∠ECD ＝180°，A B C D E FA B C D EA B CE D A B CD E∴∠EDC ＝∠EAB ，∴DC ∥AB. 又AD 不平行于BC ，∴四边形ABCD 是等腰梯形. 例5. 如图所示，在梯形ABCD 中，AB ∥CD ，AB ＝2，BC ＝3，CD ＝1. E 是AD 的中点，求证：CE ⊥BE.证明：延长CE 交BA 的延长线于F ，∵CD ∥BF ，∴∠D ＝∠EAF ，∠DCE ＝∠F. ∵DE ＝AE ，∴△CDE ≌△FAE. ∴AF ＝CD ＝1，EF ＝CE.∵AB ＝2，BC ＝3，∴AB ＋AF ＝BC. 即BF ＝BC. ∴BE ⊥CE. 1. 若等腰梯形的锐角是60°，它的两底分别为11cm ，35cm ，则它的腰长为__________cm .2. 如图所示，已知等腰梯形ABCD 中，AD ∥BC ，∠B ＝60°，AD ＝2，BC ＝8，则此等腰梯形的周长为（ ）A. 19B. 20C. 21D. 22AB CD**3. 如图所示，AB ∥CD ，AE ⊥DC ，AE ＝12，BD ＝20，AC ＝15，则梯形ABCD 的面积为（ ）A. 130B. 140C. 150D. 160ABCDE*4. 如图所示，在等腰梯形ABCD 中，已知AD ∥BC ，对角线AC 与BD 互相垂直，且AD ＝30，BC ＝70，求BD 的长.AB CD5. 如图所示，已知等腰梯形的锐角等于60°，它的两底分别为15cm 和49cm ，求它的腰长.AB CD6. 如图所示，已知等腰梯形ABCD 中，AD ∥BC ，AC ⊥BD ，AD ＋BC ＝10，DE ⊥BC 于E ，求DE 的长.ABC D E FA BCDE7. 如图所示，梯形ABCD 中，AB ∥CD ，∠D ＝2∠B ，AD ＋DC ＝8，求AB 的长.ABCD**8. 如图所示，梯形ABCD 中，AD ∥BC ，（1）若E 是AB 的中点，且AD ＋BC ＝CD ，则DE 与CE 有何位置关系？（2）E 是∠ADC 与∠BCD 的角平分线的交点，则DE 与CE 有何位置关系？AB CDE1、梯形ABCD 中，AD ∥BC ，∠B=50°，∠C=80°，BC=5，AD=3，则CD= 。
《梯形》辅助线专题训练
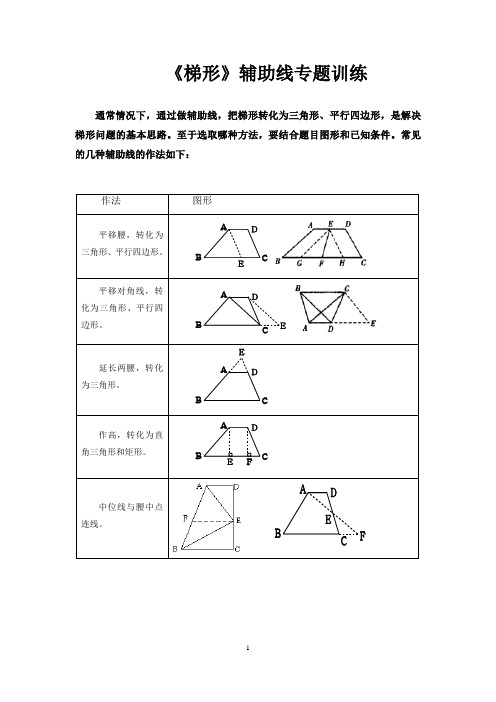
《梯形》辅助线专题训练通常情况下，通过做辅助线，把梯形转化为三角形、平行四边形，是解决梯形问题的基本思路。
至于选取哪种方法，要结合题目图形和已知条件。
常见的几种辅助线的作法如下：作法图形平移腰，转化为三角形、平行四边形。
ABCD E平移对角线，转化为三角形、平行四边形。
ABCDE延长两腰，转化为三角形。
ABCD E作高，转化为直角三角形和矩形。
ABCD EF中位线与腰中点连线。
ABCD EF一、平移1、平移一腰例1. 如图所示，在直角梯形ABCD 中，∠A ＝90°，AB ∥DC ，AD ＝15，AB ＝16，BC ＝17. 求CD 的长。
解：过点D 作DE ∥BC 交AB 于点E.又AB ∥CD ，所以四边形BCDE 是平行四边形. 所以DE ＝BC ＝17，CD ＝BE. 在R t △DAE 中，由勾股定理，得AE 2＝DE 2－AD 2，即AE 2＝172－152＝64. 所以AE ＝8.所以BE ＝AB －AE ＝16－8＝8. 即CD ＝8.例2.梯形ABCD 的上底AB=3，下底CD=8，腰AD=4，求另一腰BC 的取值范围。
解：过点B 作BM//AD 交CD 于点M ，在△BCM 中，BM=AD=4， CM=CD －DM=CD －AB=8－3=5，所以BC 的取值范围是：5－4<BC<5＋4，即1<BC<9。
2、平移两腰例3.如图，在梯形ABCD 中，AD//BC ，∠B ＋∠C=90°，AD=1，BC=3，E 、F 分别是AD 、BC 的中点，连接EF ，求EF 的长。
ABCDABCD E解：过点E 分别作AB 、CD 的平行线，交BC 于点G 、H ，可得∠EGH ＋∠EHG=∠B ＋∠C=90° 则△EGH 是直角三角形因为E 、F 分别是AD 、BC 的中点，容易证得F 是GH 的中点所以)(2121CH BG BC GH EF --==1)13(21)(21)]([21)(21=-=-=+-=--=AD BC DE AE BC DE AE BC3、平移对角线例4.已知：梯形ABCD 中，AD//BC ，AD=1，BC=4，BD=3，AC=4，求梯形ABCD 的面积。
最新梯形中的常用辅助线总结与对应练习题
. 求证： 中,
. . 求证：梯
形
是等腰梯形 .
2、平移两腰：利用梯形中的某个特殊点，过此点作两腰的平行线，把两腰转化到同一个三角形中。 ［例 2］如图，在梯形 ABCD中， AB//CD，∠D＋∠ C=90°，BC=1，AD=3，E、F 分别是 AB、CD的中点， 连接 EF，求 EF的长。
【变式】如图，在梯形
【变式 1】在等腰梯形 ABCD中， AD//BC，AD=3，BC=7，BD=5 2 ，求证： AC⊥ BD。
精品文档
精品文档
【变式 2】（平移对角线）已知梯形 ABCD的面积是 32，两底与高的和为 16，如果其中一条对角线与 两底垂直，则另一条对角线长为 _____________ ［例 4］在梯形 ABCD中， AD//BC，AC=15cm，BD=20cm，高 DH=12cm，求梯形 ABCD的面积。
D
C
A
B
三、作对角线： 即通过作对角线，使梯形转化为三角形。
［例 6］在直角梯形 ABCD中， AD//BC，AB⊥ AD，BC=CD，BE⊥CD于点 E，求证： AD=D。E
四、作梯形的高 1、作一条高，从底边的一个端点作另一条底边的垂线，把梯形转化为直角三角形或矩形。
精品文档
精品文档
［例 7］如图，在直角梯形 ABCD中， AB//DC，∠ ABC=9°0 ， AB=2DC，对角线 AC⊥BD，垂足为 F，过 点 F 作 EF//AB，交 AD于点 E，求证：四边形 ABFE是等腰梯形。
中，
，
1 EF=2(CD-AB)
， 、 为 、 的中点。求证：
3、平移对角线：一般是过上底的一个端点作一条对角线的平行线 , 与另一底的延长线相交 , 得到一个 平行四边形和三角形 , 把梯形问题转化为平行四边形和三角形问题解决．
梯形
等腰梯形常用辅助线专项练习 姓名一、选择：1、如图，在平面直角坐标中，等腰梯形ABCD 的下底在x 轴上，且B 点坐标为（4，0），D 点坐标为（0，3），则AC 长为（ ）A ．4B ．5C ．6D ．不能确定2、如图，等腰梯形ABCD 中，AD ∥BC ，AB=DC ，AD=3，AB=4，∠B=60°，则梯形的面积是（ ） A ．310 B ．320 C ．6+34 D ．12+383、如图，梯形ABCD 中，AD ∥BC ，AB=CD ．AD=2，BC=6，∠B=60°，则梯形ABCD 的周长是（ ） A ．12 B ．14 C ．16 D ．184、如图，在梯形ABCD 中，AB ∥CD ，AD=BC ，对角线AC ⊥BD ，垂足为O ，若CD=3，AB=5，则AC 的长为（ ）A ．24B ．4C ．33D ．525、如图，在等腰梯形ABCD 中，AB ∥CD ，对角线AC 平分∠BAD ，∠B=60°，CD=2cm ，则梯形ABCD的面积为（ ）cm 2．A ．33B ．6C ．36D ．126、如图，在等腰梯形ABCD 中，AD ∥BC ，对角线AC ⊥BD 于点O ，AE ⊥BC ，DF ⊥BC ，垂足分别为E 、F ，AD=4，BC=8，则AE+EF 等于（ ）A ．9B ．10C ．11D ．12 二、填空：7、如图，等腰梯形ABCD 中，AD ∥BC ，AB=AD=2，第1题第2题图第3题图第4题图第5题图第6题图8、如图，在等腰梯形ABCD 中，AB ∥CD ，AD ⊥BD ，∠A=60°，AD=2，梯形ABCD 的面积为（结果保留根号） 。
9、如图，在等腰梯形ABCD 中，AC ⊥BD ，AC=6cm ，则等腰梯形ABCD 的面积为 。
10、如图，在等腰梯形ABCD 中，AD ∥BC 且AC ⊥BD 于E ，AD=2，BC=8，则该梯形的面积为 。
八年级下册数学梯形的辅助线基础题人教版(含答案)
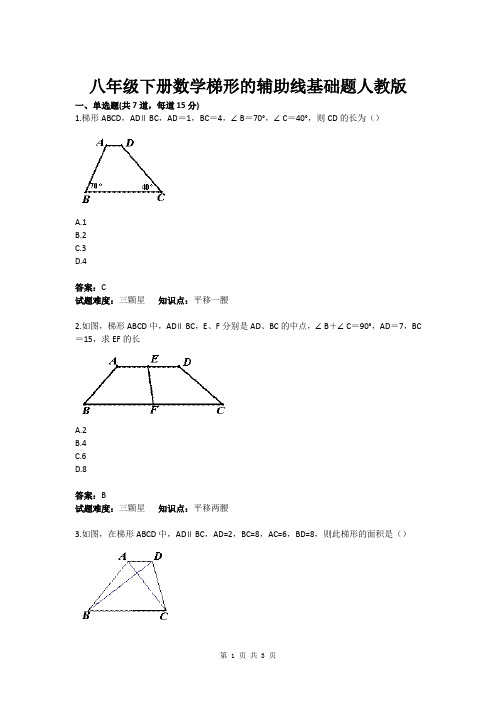
八年级下册数学梯形的辅助线基础题人教版一、单选题(共7道，每道15分)1.梯形ABCD，AD∥BC，AD＝1，BC＝4，∠B＝70°，∠C＝40°，则CD的长为（）A.1B.2C.3D.4答案：C试题难度：三颗星知识点：平移一腰2.如图，梯形ABCD中，AD∥BC，E、F分别是AD、BC的中点，∠B＋∠C＝90°，AD＝7，BC ＝15，求EF的长A.2B.4C.6D.8答案：B试题难度：三颗星知识点：平移两腰3.如图，在梯形ABCD中，AD∥BC，AD=2，BC=8，AC=6，BD=8，则此梯形的面积是（）A.24B.20C.16D.12答案：A试题难度：三颗星知识点：平移对角线4.如图，在梯形ABCD中，AD//BC，∠B=50°，∠C=80°，AD=2，BC=5，求CD的长（）A.1B.2C.3D.4答案：C试题难度：三颗星知识点：延长两腰5.梯形ABCD中，AD∥BC，AD=2，CD=，∠B=60°，∠C=45°，则梯形ABCD的周长为（）A.B.C.D.13答案：A试题难度：三颗星知识点：做高线6.如图，梯形ABCD中，AD∥BC，点E在BC上，AE=BE，点F是CD的中点，且AF⊥AB，若AD=2.7，AF=4，AB=6，则CE的长为（）A.2.2B.1.3C.2.5D.2.3答案：D试题难度：三颗星知识点：延长一腰中点与梯形一个顶点的连线7.在梯形ABCD中，AB∥CD，点M为BC的中点，DM平分∠ADC，下面结论不正确的是（）A.∠DAM=∠BAMB.DM⊥AMC.AD=BCD.AD=DC+AB答案：C试题难度：三颗星知识点：与一腰上一点有关辅助线。
黄立宗推荐-梯形辅助线的常见作法--好--
梯形辅助线的常见作法---黄立宗编排梯形是一种特殊的四边形。
它是平行四边形、三角形知识的综合，通过添加适当的辅助线将梯形问题化归为平行四边形问题或三角形问题来解决。
辅助线的添加成为问题解决的桥梁，梯形中常用到的辅助线有：（1）在梯形内部平移一腰。
例1：（如图1）已知在梯形ABCD中，AD//BC，BA=DC。
求证：B= C证明：过点D作DM//AB交BC于点M。
因为 AD//BC DM//AB 所以AB=DM因为 BA=DC 所以 DM=DCDMC= CDMC= B B= C（2）梯形外平移一腰例2：（如图2）在梯形ABCD中,AB∥DC,作□ACED延长DC交BE于F，求证:EF=FB证明：过点B作BG∥AD,交DC的延长线于G∴四边形ABGD是平行四边形∴AD=BG∵□ACED中，AD∥CE AD=CE∴CE∥BG且CE=BG ∴∠1=∠2又∵∠3=∠4 ∴⊿ECF≌⊿BGF∴:EF=FB(3)梯形内平移两腰例3 ：（如图3）在梯形ABCD中,AD∥BC,AD﹤BC,E、F分别为AD、BC的中点，且EF⊥BC，试说明∠B=∠C解：过E作EM∥AB,EN∥CD,分别交BC于M,N得□ABME ,□NCDE∴AE=BM DE=CN, ∵AE=DE ∴BM=CN又∵BF=CF ∴FM=FN∵EF⊥BC ∴EM=EN ∴∠1=∠2∵EM∥AB,EN∥CD, ∴∠1=∠B , ∠2=∠C∴∠B=∠C(4)延长两腰例4：（如图4）在梯形ABCD中, ∠B=∠C ，AD∥BC，求证：梯形ABCD是等腰梯形。
证明：延长BA,CD交于点E∵∠B=∠C ∴BE=CE∵AD∥BC ∴∠EAD=∠B ∠EDA=∠C∵∠B=∠C ∴∠EAD=∠EDA∴AB=CD结论得证（5）过梯形上底的两端点向下底作高例5：（如图5）在梯形ABCD中，DC∥AB,AD=BC,若AD=5,CD=2 ，AB=8,求梯形ABCD的面积。
解：过点D、C分别作DE⊥AB于E,CF⊥AB于F.根据等腰梯形的轴对称性可知，AE=BF.∵DC∥AB, DE⊥AB,CF⊥AB∴四边形CDEF是矩形∴DC=EF∴AE=(AB-EF)= (AB-CD)=3∴ DE===4∴=(2+8)x4=20(6)平移对角线 ---求证：对角线相等的梯形是等腰梯形。
梯形辅助线的添设方法[1]共17页文档
![梯形辅助线的添设方法[1]共17页文档](https://img.taocdn.com/s3/m/64ce657b6529647d262852b3.png)
11、不为五斗米折腰。 12、芳菊开林耀，青松冠岩列。怀此 贞秀姿 ，卓为 霜下杰 。
13、归去来兮，田蜀将芜胡不归。 14、酒能祛百虑，菊为制颓龄。 15、春蚕收长丝，秋熟靡王税。
开动脑筋
在
转
梯 形
平移腰
化 为
中
作高
常
三 角
用
形
的
补为三角形
或
作
平
辅
平移对角线
行
助
四
线
其他方法
A
2D
23
3
32
B 60°
3 E`
45 ° C
3
布置作业：
1、课本179页B组题 2、求证：对角线垂直的等腰梯形的高等于它的中位线
A F B
D G
E
C
H
31、只有永远躺在泥坑里的人，才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭，生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍，就是一下子不要学很多。——洛克
边
方
形
法
灵活应用
等
A
D
A
平
B
移
E
A
D
CB
A
E O
D
E
C D
B
FC
B
C
腰
1.以上图中相等的线段，相等的角 2.平移腰可将梯形的两腰、两底角放置在一个三角形.
作
A
D
BE
F
C
高ห้องสมุดไป่ตู้
O
补A
D
总结梯形常用辅助线及对应例题
总结梯形常用辅助线及对应例题帮你总结梯形中的辅助线1.平移梯形一腰或两腰,把梯形的腰、两底角等转移到一个三角形中,同时还得到平行四边形．【例1】分析:平移一腰BC到DE,将题中已知条件转化在同一等腰三角形中解决,即AB=2CD. 证明：过D作,交AB于E.∵ AB平行于CD,且,∴四边形形.∴是菱形.∴ 又, ∴又∴∴为等边三角.M 、∴【例2】解：过E 作EM∥AB ,EN ∥DC ,分别交BC 于N ,∵, ∴是直角三角形,∵,,∴. ∵、分别是、的中点,∴ 为的中点,∴ .2.延长梯形的两腰,使它们交于一点,可得到两个相似三角形或等腰三角形、直角三角形等进一步解决问题．【例3】分析：条件是两个梯形的面积相等,而结论是三线段长的平方关系,如果延长两腰交于一点,就可得到三个相似的三角形,再利用相似三角形的面积比与相似比的关系变形就可得出结论．证明：延长、使它们相交于点∵,∴ ∴. 同理,∵ 故得∴3.从梯形上底的两端向下底引垂线作高,可以得到一个矩形和两个直角三角形．然后利用构造的直角三角形和矩形解决问题．【例4】.分析:过上底向下底作两高,构造Rt△,然后利用两三角形全等解决问题.证明：分别过D、C、作AB的垂线,垂足分别为E、F.∵∴≌, ∴ .∴. 又,4.平移一条对角线一般是过上底的一个端点作一条对角线的平行线,与另一底的延长线相交,得到一个平行四边形和三角形,把梯形问题转化为平行四边形和三角形问题解决．【例5】．分析：由梯形中位线性质得,欲证 ,只要证、和．过点作 ,交的延长线于 ,就可以把单多了．证明：过点作四边形移到三角形中,再证明等式成立就简交的延长线于点,,则是平行四边形．∴∵ 四边形又∵是等腰梯形,∴,∴,∴ ,∴,∴. ∵ ,∴又∵ ,∴ .【例6】.证明：过D作边形.∴∴.∴ 于是,可得,交BA延长线于E.则四边形又∴,是平行四∴梯形ABCD是等腰梯形.5.遇到梯形一腰中点的问题可以作出梯形的中位线,中位线与上、下底都平行,且三线段有数量关系. 或利用“等积变形”,连结梯形上底一端点和另一腰中点,并延长与下底延长线交于一点,构成三角形解决问题．【例7】证明：取,∴的中点F,连结FE.则. ∴.∵6.当遇到以上的梯形辅助线添加后不能解决问题时,可以特题特解,结合具体问题中的具体条件,寻求特殊的方法解决问题.比如可将对角线绕中点旋转、利用一腰中点旋转,交、将梯形补成平行四边形或三角形问于E.则又N是AC的中点, ∴题.【例9】证明：连结并延长.∴, 故取一腰的中点,连结顶点和这个中点并延长与对边的延长线相交,可得两个全等三角形．【例10】分析：要证明的延长线交于,、 ,,可以利用,得到交于点为中点,延长与,再证明 F,显然即可．证明：延长．∴. 又∵, ,∴ ,∴, ∴ .是线段, ∴的垂直平分线．∴评注：添加辅助线后,沟通了得出、与的联系,由线段垂直平分线性质,从而问题获得解决．利用一腰中点旋转【例11】证明：延长AE、BC相交于点F.易证∵,∴底边上的高.∴.即∴.∴BE是等腰,说明：在图5中,在图6中,相当于由是由绕点E旋转得到.得到；绕点E旋转【例12】.分析：与梯形ABCD的面积关系不明显,如果利用梯形助特点把它补成如图7的平行四边形,它们之间的关系就清晰了．梯形补成平行四边形,各种关系明显、直观,解题思路清晰．证明：延长,使,延长,使为；则的中点,连结,,则四边形与交于点.连结是平行四边形．、,则.∵ , 是中点,∴ 为中点且是中点．∴四边形是平行四边形,∴ ,∴感谢您的阅读，祝您生活愉快。
八级数学秋季班第7讲梯形进阶之梯形辅助线大揭秘拔高练习(北师版)
八级数学秋季班第7讲梯形进阶之梯形辅助线大揭秘拔高练习（北师版）八年级数学秋季班第7讲梯形进阶之梯形辅助线大揭秘拔高练习（北师版）试卷简介:本测试卷共8道题，全面考察梯形辅助线的做法，分三个板块，第一板块：梯形辅助线复习，共有9中辅助线的做法；第二板块：梯形辅助线的应用，充分考察等腰梯形和直角梯形的知识；第三板块：梯形动点问题，是中考题的常考题型和重难点、学习建议:先充分的了解梯形各种辅助线的做法和原理一、单选题(共1道，每道10分)1.（2011安徽）如图，四边形ABCD中，∠BAD=∠ADC=90°，AB=AD=，CD=，点P在四边形ABCD的边上，若P到BD的距离为，则点P的个数为( )A.1B.2C.3D.4二、填空题(共3道，每道10分)1.如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，BD⊥DC，BD=DC，CE平分∠BCD，交AB于点E，交BD于点H，EN∥DC交BD于点N．下列结论：①BH=DH；②③其中正确的是（）2.如图，菱形ABCD由6个腰长为2，且全等的等腰梯形镶嵌而成，则线段AC的长为_______.3.（2010河南）如图，在梯形ABCD中，AD∥BC，E是BC的中点，AD=5，BC=12，CD= ，∠C=45°，点P是BC边上一动点，设PB的长为x．（1）当x的值为____________时，以点P、A、D、E为顶点的四边形为直角梯形；（2）当x的值为____________时，以点P、A、D、E为顶点的四边形为平行四边形；；（3）点P在BC边上运动的过程中，以P、A、D、E为顶点的四边形能否构成菱形？试说明理由．三、解答题(共4道，每道15分)1.（2011山东菏泽）如图，在梯形ABCD中，AD∥BC，∠B=90°，∠C=45°，AD=1，BC=4，E为AB中点，EF∥DC交BC于点F，求EF的长.2.（2011重庆）如图，梯形ABCD中，AD∥BC，∠DCB=45°，CD=2，BD⊥CD．过点C作CE⊥AB 于E，交对角线BD于F，点G为BC中点，连结EG、AF．（1）求EG的长；（2）求证：CF=AB+AF．3.如图，四边形ABCD为一梯形纸片，AB∥CD，AD=BC．翻折纸片ABCD，使点A与点C重合，折痕为EF．已知CE⊥AB．（1）求证：EF∥BD；（2）若AB=7，CD=3，求线段BC，BD的长．4.（2011四川南充）如图，等腰梯形ABCD中，AD∥BC，AD=AB=CD=2，∠C=60°，M是BC的中点.（1）求证：△MDC是等边三角形；（2）将△MDC绕点M旋转，当MD(即MD′)与AB 交于一点E,MC（即MC＇)同时与AD交于一点F 时，点E,F和点A构成△AEF.试探究△AEF的周长是否存在最小值.如果不存在，请说明理由；如果存在，请计算出△AEF周长的最小值.。
梯形、等腰梯形常见辅助线
专题三 梯形、等腰梯形常见辅助线★★【知识目标清单】♦1、梯形：一组对边平行而另一组对边不平行的四边形。
♦ 2、等腰梯形的性质与判定： (1)性质：等腰梯形的两腰相等，两底平行； 等腰梯形同一底上的两个角相等，对角线相等。
(2 )判定：同一底上的两个角相等的梯形是等腰梯形；对角线相等的梯形是等腰梯形。
♦ 3、解决梯形的计算与证明问题关键在于转化 ---梯形中常见的辅助线：【分层练习】A 组----基础演练1、四边形 ABCD 中，若.A: . B: . C : . D =3: 3:1:5，则这个四边形是( )2、在梯形中，AB//CD , AD =DC =CB =2 , . A =45 ,则这个梯形的周长为 () 3、如图，在等腰梯形 ABCD 中，.BCD =60 , AD // BC ，且 AD 二 DC , E 、F 分 别在AD 、DC 的延长线上，且 DE =CF , AF 、 (1) 求证：AF =BE ；(2) 请你猜测.BPF 的度数，并证明你的结论。
B 组---能力拓展1、如图：点E 是梯形ABCD 的腰CD 的中点，ABE 的面积是6cm 2,则梯形ABCD 的面积为 ________________ 2、如图：四边形 ABED 与四边形 AFCD 都是平行四边形，AF 和DE 相交成直角,2 AG =3cm , DG =4cm , □ ABED 的面积是36cm ，则四边形ABCD 的周长是（ ） A 、49cm B 、43cm C 、41cm D 、46cm3、如图：在梯形 ABCD 中，AD// BC , AB _ AC , B =45 , AD = _ 2 , BC =4、. 2 ,A 、梯形B 、等腰梯形C 、直角梯形D 、任意四边形C 、10D 、10-2.2BE 交于点P 。
求DC的长。
梯形辅助线专练
例 1.如图所示，在梯形 ABCD 中，AD // BC , AB = 8, DC = 6,Z B = 45°, BC = 10, 求梯形上底AD 的长. 分析：作AE 丄BC , DF 丄BC ,垂足分别为E 、F ,这样可构造两个直角三角形 . 解：分别过点A 、D 作AE 丄BC , DF 丄BC ,垂足分别为E 、F ,则四边形AEFD 是矩形. 在 Rt △ ABE 中，•••/ B = 45°,「. AE = BE. 设 AE = BE = x ,贝V AB = x = 8, x = 4,「. AE = BE = DF = 4, 在 Rt △ DFC 中，CF = = 2,AD = EF = BC — BE — CF = 10— 4 — 2= 8-4. 例2.如图所示，在直角梯形 ABCD 中，/ A = 90 °, =17.求CD 的长. 解：过点D 作DE // BC 交AB 于点E. 又AB // CD ，所以四边形 BCDE 是平行四边形. 所以 DE = BC = 17, CD = BE. 在Rt △ DAE 中，由勾股定理，得 AE 2= DE 2 — AD 2,即即 AE 2= 172— 152= 64. 所以AE = 8. 所以 BE = AB — AE = 16 — 8 = 8. 即 CD = 8. 例3.如图所示，在等腰梯形ABCD 中，AD // BC,对角线 的面积.解：过点D 作DE // AC 交BC 的延长线于点 E. 又 AD // BC , .四边形ACED 是平行四边形. --AC = DE , S A ADC = S A ECD .-S AADC =S ADAB ，…S ADAB =S AECD..S A DBE = S 梯形 ABCD .•••四边形ABCD 是等腰梯形，••• AC = BD. •/ AC = DE ,• BD = DE = 6cm.•/ AC 丄 BD , AC // DE , • DE 丄 BD.2• S 梯形 ABCD = S A DBE = BD • DE = x 6X 6= 18 ( cm )AB // DC , AD = 15, AB = 16, BC B AC 丄 BD ,BD = 6cm.求梯形 ABCD 例4.如图所示，四边形ABCD 中，AD 不平行于BC ,AC = BD ,AD = BC.判断四边形 ABCD 的形状，并证明你的结论. 解：四边形ABCD 是等腰梯形. 证明：延长 AD 、BC 相交于点E ，如图所示. •/ AC = BD , AD = BC , AB = BA , •△ DAB BA CBA.• / DAB =Z CBA. • E A = EB.又 AD = BC ,• DE = CE ,Z EDC = Z ECD.而/ E +Z EAB + Z EBA =Z E +Z EDC + Z ECD = 180°,•••/ EDC = Z EAB ,••• DC // AB.例5.如图所示，在梯形ABCD中，求证：CE丄BE.证明：延长CE交BA的延长线于•/ CD // BF，•/ D = Z EAF，/ DCE = Z F.•/ DE = AE ,•••△CDE ◎△ FAE.AF = CD = 1 , EF= CE.•/ AB = 2, BC = 3 , • AB + AF = BC.即BF = BC. • BE 丄CE.*4.如图所示，在等腰梯形AD = 30, BC = 70,求BD 的长.5. 如图所示，已知等腰梯形的锐角等于60°,它的两底分别为15cm和49cm,求它的腰长.6. 如图所示，已知等腰梯形ABCD中，AD // BC , AC丄BD , AD + BC = 10, DE丄BC于E,求DE的长.1. 若等腰梯形的锐角是60°长为 ___________ cm.2. 如图所示，已知等腰梯形腰梯形的周长为（A. 19，它的两底分别为11cm, 35cm,则它的腰ABCD 中，AD // BC，/ B = 60°, AD = 2, BC = 8,则此等)B. 20 D. 22**3.如图所示，积为（）A. 130B.140C.150AB //CD ,C. 21AE 丄DC , AE = 12, BD = 20 , AC = 15，则梯形ABCD 的面D. 160C又AD不平行于BC,「.四边形ABCD是等腰梯形. AB //CD , AB = 2, BC = 3, CD = 1. E 是AD 的中点,F,中，已知AD // BC,对角线AC与BD 互相垂直，且ABCD△n7. 如图所示，梯形ABCD 中，AB // CD，/ D= 2/B , AD + DC = 8,求AB 的长.**8.如图所示，梯形ABCD中，AD // BC, （1）若E是AB的中点，且AD + BC = CD , 则DE与CE有何位置关系？（2）E是/ ADC与/ BCD的角平分线的交点，贝U DE与CE 有何位置关系？1、梯形ABCD 中，AD // BC, / B=50。
梯形中常见的辅助线(含答案)
梯形中常见的辅助线内容基本要求略高要求较高要求梯形会识别梯形、等腰梯形：了解等腰梯形的性质和判定.掌握梯形的槪念，会用等腰梯形的性质和判定解决简单问题.例我们可以看到，梯形本身的性质并不多，所以实际解梯形的问题时，往往通过添加辅助线将梯形分成三角形或平行四边形，三角形是最简单的直线形，而平行四边形具有很好的对称性质•下而给出几个常见的添加辅助线的方法.1.作梯形的高：一般是过梯形的一个顶点作高，英好处是将梯形分成一个直角三角形和一个直角梯形，从而可以用勾股;4^理，如果过梯形的两个顶点分别作高•则会出现矩形•2.过梯形的一个顶点作另一腰的平行线：这样便将梯形分成了一个平行四边形和一个三角形，这样做的好处是可以将两条腰拉到同一个三角形中，并且三角形的另一条边恰好是梯形的两底之差，从而将问题集中到三角形中•3.延长梯形的两腰交于一点：这样做可以同样地使问题转化为三角形的问题.4.过梯形一腰的中点作另一腰的平行线：可以将梯形等积变换成一个平行四边形.5.连接梯形一个顶点和另一腰上的中点并延长交另一底边：可以将梯形等积变换成一个三角形.常见的辅助线添加方式如下:梯形中的辅助线较多，其实质是采用割补法将梯形问题划归为三角形、平行四边形问题处理.解题时要根据题目的条件和结论来确总作哪种辅助线.常见辅助线1.梯形问题通常是通过分割和拼接转化为三角形或平行四边形，英分割拼接的方法有如下几种（如图）:1,把梯形分成一个平行四边形和一个三角形（图1所示）:【答案】（1）作一腰的平行线； （2）作另一底边的垂线： （3）作对角线的平行线:（4）交于一点：（5）对称中心： （6）对称轴.【例1】 等腰梯形ABCD 中，AD//BC,若AD=3, AB=4・ BC=7,则ZB= 【答案】60° 如图，直角梯形ABCD 中，AB//CD. CB 丄AB, △ABD 是等边三角形，若AB=2,则BC=在梯形ABCD 中，AD//BC. AD=5, BC=7.若E 为DC 的中点，対线交BC 的延长线于F 点，则BF= •梯形ABCD 中.AD//BC,若对角线AC 丄BD ■且AC=5cm. BD=12cm,则梯形的而积等于（（1）平移一腰，即从梯形的一个顶点（2）从同一底的两端. ,把梯形分成一个矩形和两个宜角三角形（图2所示）;（3）平移对角线，即过底的一端图2，可以借助新得的平行四边形或三角形来研究梯形（图3所示）:（4）延长梯形的两腰.图3,得到两个三角形，如果梯形是等腰梯形，则得到两个等腰三角形（图4所示）:（5）以梯形一腰的中点为.图4,作某图形的中心对称图形（图5、图6所（6）以梯形一腰为.图5 图6,作梯形的轴对称图形（图7所【例2】【答案】 73【例3】【答案】 12 【例4】 A. 30cw- B. 60CW' C- 90cm~2D- } 69 cm-【例10】如图，等腰梯形ABCD 中，AB//CD.对角线AC 平分Z BAD, ZB=60。
八年级数学下册梯形辅助线的六种做法课标试题
卜人入州八九几市潮王学校梯形辅助线的做法一、平移一条对角线。
1、 如图，在梯形ABCD 中，AD ∥BC ，AB ＝CD ，AC ⊥BD ，AD ＝6,BC ＝8,那么梯形的高为。
2、 如图，在梯形ABCD 中，AD ∥BC ，AC ⊥BD ，AC=8，DB=6，那么此梯形的高为。
3、 如图，在梯形ABCD 中，AD ∥BC ，AB ＝CD ，对角线AC ⊥BD ，BD=6，那么梯形的高为。
4、 如图，在梯形ABCD 中，AD ∥BC ，AB ＝CD ，EF 是中位线，AC ⊥BD ，DG ⊥BC 于G ，求证：EF=DG 。
5、 在梯形ABCD 中，AD ∥BC ，AB ＝CD ，AC ⊥BD ，AB=4，∠ABC=60°求：梯形ABCD 的周长。
6、 〔本小题总分值是5分〕如图，在梯形ABCD 中，AD ∥BC ，CD AB =．假设AC ⊥BD ，AD+BC =310，且︒=∠60ABC ，求CD 的长．7、 在梯形ABCD 中，AD ∥BC ，假设两底AD 、BC 的长分别为2、8，两条对角线BD=6，AC=8，求梯形的面积。
8、 ：如图，在梯形ABCD 中，AD ∥BC ，AC=DB 。
求证：AB=DC 。
9、 ：等腰梯形ABCD 中，AD ∥BC ，对角线AC=BC+AD ，求∠DBC 的度数。
二、平移一腰。
10、 ：在梯形ABCD 中，AD ∥BC ，AD=3，AB=7，BC=6，那么第四边CD 的取值范围是多少？DCA BDCBAGFEDCBADCBAA BCDE CBA DBCADE11、 ：如图，在梯形ABCD 中，AD ∥BC ，AB=AD =2，∠A=60°，BC =4，求CD 的长．12、 ：如图，在梯形ABCD 中，∠A+∠D=90°，M 、N 是BC ，AD 的中点。
求证：MN=)(21BC AD -。
三、从小底的两端向大底引垂线。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
梯形辅助线专题训练题---黄立宗编排
考号 姓名
1、如图，已知在梯形ABCD 中，AB ∥DC ，∠D=60°，∠C=45°，AB=2，AD=4，求梯形ABCD 的面积．
2、在梯形ABCD 中，AD//BC ，AB=DC=AD=2， BC=4，求∠B 的度数及AC 的长。
3、如图所示，已知等腰梯形ABCD 中，AD ∥BC ，∠B ＝60°，AD ＝2，BC ＝8，求等腰梯形的周长。
A
B C
D
4、 如图所示，AB ∥CD ，AE ⊥DC ，AE ＝12，BD ＝20，AC ＝15，求梯形ABCD 的面积。
A
B
C
D
E
5、 如图所示，在等腰梯形ABCD 中，已知AD ∥BC ，对角线AC 与BD 互相垂直，且AD ＝30，BC ＝70， 求BD 的长.
A B
C
D C
D
A B
A
B C
D
6、 如图所示，已知等腰梯形的锐角等于60°，它的两底分别为15cm 和49cm ，求它的腰长.
A
B C
D
7、 如图所示，已知等腰梯形ABCD 中，AD ∥BC ，AC ⊥BD ，AD ＋BC ＝10，DE ⊥BC 于E ，求DE 的长.
A
B
C
D
E
8、已知：如图，梯形ABCD 中，AD ∥BC ，AB=DC ，∠BAD 、∠CDA 的平分线AE 、DF 分别交直线BC 于点E 、F ．
求证： CE=BF ．
9、如图，在梯形A B C D 中，A D B C ∥，9038BD C D BD C AD BC =∠===，°，，
．求A B 的长．
B
C
A
D
E
10、如图6，在梯形A B C D 中，A D B C ∥，90A ∠=︒，︒=∠45C ，DE=EC ，AB=4,AD=2，求B E 的长．
11、已知：如图，梯形ABCD 中，DC ∥AB ，AD=BC ，对角线AC 、BD 交于点O ，∠COD=60°，若CD=3，
AB=8，求梯形ABCD 的高．
12、已知如图，直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD=2，BC=DC=5，点P 在BC 上移动，则当PA+PD 取最小值时，△APD 中边AP 上的高为多少.
13、如图，在梯形ABCD 中，∥ADBC ，AB=CD ，E 、F 、G 、H 分别为AB 、BC 、CD 、
DA 的中点，小王
B
C
D
O
A
12题图
根据以上条件猜测出四边形EFGH是菱形，你同意他的观点吗？请回答，并说明理由。
14、如图，过正方形ABCD对角线BD上一点P，作PE⊥BC于E，作PF⊥CD于F，连结AP、EF。
（1）试说明AP=EF的道理；（2）猜想AP与EF有怎样的位置关系，并说明理由。
15、如图，梯形ABCD中，AD∥BC，AB=CD，BG⊥CD于G，P是BC上任意一点，作PE⊥AB，
PF⊥CD。
求证：PE＋PF=BG。
16、如图所示，梯形ABCD中，AD∥BC，∠B=90°，AB=14cm，AD=8cm，BC=21cm，动点P从点
A开始沿AD边向点D以每秒1cm的速度移动，动点Q从点C开始沿CB边向B点以每秒2cm的速度移动，如果P、Q分别从A、C同时出发，设移动时间t秒，求t为何值时，梯形PQCD是等腰梯形。
17、已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF的延长线交DC
于点E 。
求证：（1）△BFC ≌△DFC ；（2）AD=DE 。
18、如图，在直角梯形ABCD 中，,8,24,90,//0cm AB cm AD B BC AD ===∠
cm BC 26=，动点P 从A 开始沿AD 边向D 以s cm /1的速度运动；动点Q 从点C 开始沿CB 边向B
以s cm /3的速度运动。
P 、Q 分别从点A 、C 同时出发，当其中一点 到达端点时，另外一点也随之停止运动，设运动时间为ts 。
（1）当t 为何值时，四边形PQCD 平行为四边形？ （2）当t 为何值时，四边形PQCD 为等腰梯形？ （3）当t 为何值时，四边形PQCD 为直角梯形？。