等积转换法
九年级数学人教版(上册)小专题15 四种方法求阴影部分的面积

方法 2 和差法 ★直接和差法
将不规则阴影部分的面积看成是以规则图形为载体的一部分, 其他部分空白且为规则图形,此时采用整体作差法求解.如图:
⇨S 阴影=S△ABC-S 扇形 CAD
⇨ S阴影=S△ABO-S扇形COD
2(. 2021·包头)如图,在 Rt△ABC 中,∠ACB=90°,AB= 5,
方法 4 容斥原理
有的阴影部分面积是由两个基本图形互相重叠得到的.常用的方 法是:两个基本图形的面积-被重叠图形的面积=组合图形的面积.
10.如图,在 Rt△ABC 中,∠ACB=90°,∠A=30°,AC= 3,
分别以点 A,B 为圆心,AC,BC 的长为半径画弧,分别交 AB 于点
D,E,则图中阴影部分的面积是51π2-
与 AB 相交于点 F,连接 OE,OF,则图中阴影部分的面积是
7 2
3-43π .
★构造和差法
先将不规则阴影部分与空白部分组合,构造规则图形或分割后为 规则图形,再进行面积和差计算.如图:
4(. 2021·吉林)如图,在 Rt△ABC 中,∠C=90°,∠A=30°, BC=2.以点 C 为圆心,CB 长为半径画弧,分别交 AC,AB 于点 D, E,则图中阴影部分的面积为 23π- 3 (结果保留 π).
3 2
.
11.如图,正方形 ABCD 的边长为 3,以点 A 为圆心,2 为半径 作圆弧,以点 D 为圆心,3 为半径作圆弧.若图中阴影部分的面积分 别为 S1,S2,则 S1-S2=134π-9 .
BC=2,以点 A 为圆心,AC 长为半径画弧,交 AB 于点 D,交 AC
于点 C,以点 B 为圆心,AC 长为半径画弧,交 AB 于点 E,交 BC
2024年中考数学复习课件---微专题11 求阴影部分面积常见方法

2.如图,在△ABC中,∠A=90°,AB=6,AC=8,分别以点B和C为圆心
的两个等圆外切,则图中阴影部分面积为
.
1
2
微专题11
类型二
返回类型清单
求阴影部影部分看成两个规则图形的和或差.
S阴影=S△ABC-S扇形CAD
S阴影=S△AOC+S扇形COB
容斥原理
方法指导
有的阴影部分面积是由两个基本图形相互重叠得到的.常用的方法是:两个基本
图形的面积之和-被重叠图形的面积=组合图形的面积.
11
12
微专题11
求阴影部分面积常见方法
返回类型清单
对应练习
11.如图,正方形ABCD的边长为8,以D为圆心,6为半径作圆弧;以C为
圆心,8为半径作圆弧.若图中阴影部分的面积分别记为S1,S2,则
微专题11
求阴影部分面积常见方法
微专题11
求阴影部分面积常见方
法
类
型
清
单
类型一
直接公式法
类型二
和差法
类型三
等积转换法
类型四
容斥原理
微专题11
返回类型清单
求阴影部分面积常见方法
类型一
直接公式法
方法指导
阴影部分是一个规则的几何图形,根据已知条件可以直接利用规则几何图形的
面积公式计算.
S阴影=S扇形EMFN
B. π
C. π
D. π+
)
7
8
9
10
微专题11
返回类型清单
求阴影部分面积常见方法
8.(2022·毕节威宁县模拟)如图,AB为☉O的直径,将沿BC翻折,翻折
公务员考试行测技巧:4种方法求解阴影面积

公务员考试行测技巧:4种方法求解阴影面积一、求阴影部分面积的核心思想需要求的阴影部分通常是不规则图形,需要将其转换为规则图形进行求解。
二、求阴影部分面积的方法1、割法(将不规则图形分割成两个或者多个规则图形进行求解)2、补法(将不规则图形补成一个大的规则图形,再减掉非阴影部分的面积)3、等积转换法(利用等底同高的图形相等的面积进行转换,求出未知量)4、特值法(图形中某一点或某几个点的位置具有任意性)例1、下图中的甲和乙都是正方形。
BE=6厘米,EF=4厘米。
求阴影部分ABC的面积是多少平方厘米?A、20B、24C、21D、18方法1、割法:以AH为底,求三角形ABH和ACH的面积方法2、割法:以CI为底,求三角形AIC和BIC的面积方法3、补法:补成大长方形BGJF,再减掉三角形ABG、BCF、AJC的面积。
方法4、等积转换:等底同高的三角形面积相等,三角形ABC的面积等于三角形ABE 的面积。
方法5、割法:暂时分割掉三角形ADC,阴影部分的面积就等于AGBE+CDEF-ABG-BCF+ADC。
方法6、补法:(1)延长AC交BF的延长线于K,阴影部分面积等于ABK-CBK(2)延长BC交GA的延长线于L,阴影部分面积等于ALB-ALC(3)延长BA交FC的延长线于N,阴影部分面积等于NCB-NCA方法7、如果想不到以上方法就按照真实长度用直尺画出图形,量出阴影三角形的底和高,进行求解。
例2、图中长方形的面积为35平方厘米,左边直角三角形的面积为5平方厘米,右上角直角三角形的面积为7平方厘米,那么中间三角形(阴影部分)的面积是多少平方厘米?A、12.5B、13.5C、15.5D、17.5特值法:点E、F具有任意性,所以设AB=5,AD=7,则BE=2,CE=5,DF=2,CF=3,S▲CEF=×CE×CF=×5×3=7.5,阴影部分面积=35-5-7-7.5=15.5。
几何变换由三角形的面积公式易得等底等高的三角形面积相等
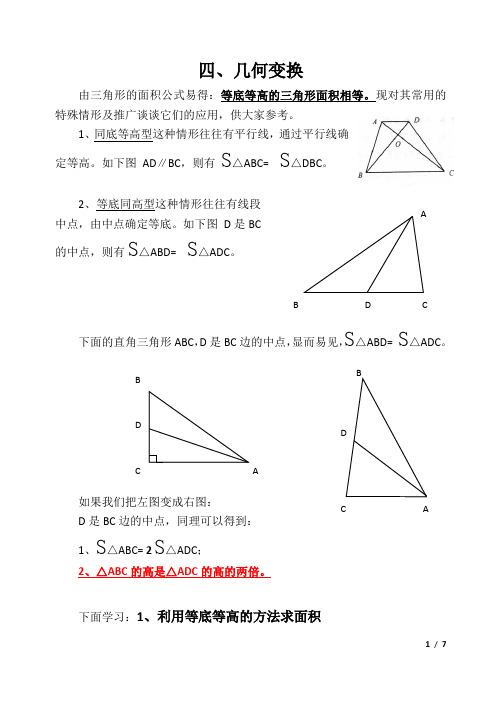
四、几何变换由三角形的面积公式易得:等底等高的三角形面积相等。
现对其常用的特殊情形及推广谈谈它们的应用,供大家参考。
1、同底等高型这种情形往往有平行线,通过平行线确定等高。
如下图 AD ∥BC ,则有S △ABC= S △DBC 。
2、等底同高型这种情形往往有线段中点,由中点确定等底。
如下图 D 是BC 的中点,则有S △ABD= S △ADC 。
下面的直角三角形ABC ,D 是BC 边的中点,显而易见,S △ABD= S △ADC 。
如果我们把左图变成右图: D 是BC 边的中点,同理可以得到: 1、S △ABC= 2 S△ADC ;2、△ABC 的高是△ADC 的高的两倍。
下面学习:1、利用等底等高的方法求面积AB D CB DC A BDC A例1如图,三角形ABC中,如果BD=DE=EF=FC,BG=GH=HA,三角形DEG的面积是2平方厘米,求三角形ABC的面积. 。
解法一:连结GF、GC。
由△GBD与△GDE、△GEF与△GFC分别都是等底同高的三角形知,S△GBC=4S△GDE=4×2=8平方厘米。
BG=GH=HA,即G是AB的三分之一点,同理可得,S△ABC=3 S△GBC=3×8=24平方厘米。
解法二:由于BD=DE=EF=FC,即DE=BC,BG=GH=HA,可得,△GDE的高是△ABC 的高的。
所以S△GDE = ×S△ABC,解得,S△ABC=24平方厘米。
小结:看到谁是谁的几分之几或是几倍(中点、三分之一点),有时是谁等于谁,立刻要判断两者是否属于同一条线上?是,就要通过添加辅助线构造△,利用等底等高的方法求解。
2、用等积转换的方法求面积左右要利用等积转换的方法求面积,常常会用到上面学的S△ABC=S△DBC,大家都减掉相同的S△BOC,剩下的S△AOB= S△DOC。
对角线与两腰围成部分面积相等,通常讲的左=右。
例2 如图,正方形ABCD的边长是8厘米,正方形GCEF的边长是6厘米,求图中阴影部分的面积。
2020版 高考大题增分课4 立体几何中的高考热点问题

(四)立体几何中的高考热点问题[命题解读] 1.立体几何是高考的必考内容,几乎每年都考查一个解答题,两个选择或填空题,客观题主要考查空间概念,三视图及简单计算;解答题主要采用“论证与计算”相结合的模式,即利用定义、公理、定理证明空间线线、线面、面面平行或垂直,并与几何体的性质相结合考查几何体的计算.2.重在考查学生的空间想象能力、逻辑推理论证能力及数学运算能力.考查的热点是以几何体为载体的垂直、平行的证明、平面图形的折叠、探索开放性问题等;同时考查转化化归思想与数形结合的思想方法.以空间几何体为载体,考查空间平行与垂直关系是高考的热点内容,并常与几何体的体积计算交汇命题,考查学生的空间想象能力、计算与数学推理论证能力,同时突出转化与化归思想方法的考查,试题难度中等.【例1】(本小题满分12分)(2019·哈尔滨模拟)如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.(1)证明:平面AEC⊥平面BED;(2)若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为63,求该三棱锥的侧面积.[信息提取]看到四边形ABCD为菱形,想到对角线垂直;看到三棱锥的体积,想到利用体积列方程求边长.[规范解答](1)证明:因为四边形ABCD为菱形,所以AC⊥BD.因为BE⊥平面ABCD,AC⊂平面ABCD,所以AC⊥BE. 2分因为BD∩BE=B,故AC⊥平面BED.又AC⊂平面AEC,所以平面AEC⊥平面BED. 4分(2)设AB=x,在菱形ABCD中,由∠ABC=120°,可得AG=GC=32x,GB=GD=x2.因为AE⊥EC,所以在Rt△AEC中,可得EG=32x. 6分由BE ⊥平面ABCD ,知△EBG 为直角三角形,可得BE =22x .由已知得,三棱锥E -ACD 的体积V 三棱锥E -ACD =13×12·AC ·GD ·BE =624x 3=63,故x =2.9分从而可得AE =EC =ED = 6.所以△EAC 的面积为3,△EAD 的面积与△ECD 的面积均为 5.故三棱锥E -ACD 的侧面积为3+2 5. 12分 [易错与防范] 易错误区:1.在第(1)问中,易忽视条件BD ∩BE =B .AC ⊂平面AEC 等条件,推理不严谨,导致扣分.2.在第(2)问中,需要计算的量较多,易计算失误,或漏算,导致结果错误. 防范措施:1.在书写证明过程中,应严格按照判定定理的条件写,防止扣分.2.在计算过程中,应牢记计算公式,逐步计算,做到不重不漏.[通性通法] 空间几何体体积的求法(1)若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解.其中,等积转换法多用来求三棱锥的体积.(2)若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解.如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB =AD =AC =3,P A =BC =4,M 为线段AD 上一点,AM =2MD ,N 为PC 的中点.(1)证明:MN ∥平面P AB ;(2)求四面体N -BCM 的体积.[解] (1)证明:由已知得AM =23AD =2.取BP 的中点T ,连接AT ,TN ,由N 为PC 中点知TN ∥BC ,TN =12BC =2.又AD ∥BC ,故TN AM ,四边形AMNT 为平行四边形,于是MN ∥AT . 因为AT ⊂平面P AB ,MN ⊄平面P AB ,所以MN ∥平面P AB .(2)因为P A ⊥平面ABCD ,N 为PC 的中点,所以点N 到平面ABCD 的距离为12P A .取BC 的中点E ,连接AE .由AB =AC =3得AE ⊥BC ,AE =AB 2-BE 2=5.由AM ∥BC 得点M 到BC 的距离为5,故S △BCM =12×4×5=2 5.所以四面体N -BCM 的体积V N -BCM =13×S △BCM ×P A 2=453.求点到平面的距离(几何体的高)求点到平面的距离(几何体的高)涉及到空间几何体的体积和线面垂直关系,是近几年高考考查的一个重要方向,重点考查学生的转化思想和运算求解能力.【例2】 (2019·开封模拟)如图,在四棱锥P -ABCD 中,底面ABCD 是菱形,且∠DAB=60°,P A=PD,M为CD的中点,平面P AD⊥平面ABCD.(1)求证:BD⊥PM;(2)若∠APD=90°,P A=2,求点A到平面PBM的距离.[解](1)证明:取AD中点E,连接PE,EM,AC,∵底面ABCD是菱形,∴BD⊥AC,∵E,M分别是AD,DC的中点,∴EM∥AC,∴EM⊥BD.∵P A=PD,∴PE⊥AD,∵平面P AD ⊥平面ABCD ,平面P AD ∩平面ABCD =AD ,∴PE ⊥平面ABCD ,∴PE ⊥BD ,∵EM ∩PE =E ,∴BD ⊥平面PEM ,∵PM ⊂平面PEM ,∴BD ⊥PM .(2)连接AM ,BE ,∵P A =PD =2,∠APD =90°,∠DAB =60°,∴AD =AB=BD =2,PE =1,EM =12AC =3,∴PM =PB =1+3=2.在等边三角形DBC 中,BM =3,∴S △PBM =394,S △ABM =12×2×3= 3.设三棱锥A -PBM 的高为h ,则由等体积可得13·394h =13×3×1,∴h =41313,∴点A 到平面PBM 的距离为41313.如图,四棱锥P-ABCD中,底面ABCD为矩形,P A⊥平面ABCD,E为PD 的中点.(1)证明:PB∥平面AEC;(2)设AP=1,AD=3,三棱锥P-ABD的体积V=34,求点A到平面PBC的距离.[解](1)证明:设BD与AC的交点为O,连接EO.因为四边形ABCD为矩形,所以O为BD的中点.又E为PD的中点,所以EO∥PB.因为EO⊂平面AEC,PB⊄平面AEC,所以PB∥平面AEC.(2)三棱锥P-ABD的体积V=16P A·AB·AD=36AB,由V=34,可得AB=32.由题设知BC⊥AB,BC⊥P A,所以BC⊥平面P AB,在平面P AB内作AH⊥PB交PB于点H,则BC⊥AH,故AH⊥平面PBC.又AH=P A·ABPB=P A·ABP A2+AB2=31313.所以点A到平面PBC的距离为313 13.是否存在某点或某参数,使得某种线、面位置关系成立问题,是近几年高考命题的热点,常以解答题中最后一问的形式出现,一般有三种类型:(1)条件追溯型.(2)存在探索型.(3)方法类比探索型.【例3】(2018·秦皇岛模拟)如图所示,在四棱锥P-ABCD中,底面ABCD 是边长为a的正方形,侧面P AD⊥底面ABCD,且E,F分别为PC,BD的中点.(1)求证:EF∥平面P AD;(2)在线段CD上是否存在一点G,使得平面EFG⊥平面PDC?若存在,请说明其位置,并加以证明;若不存在,请说明理由.[解](1)证明:如图所示,连接AC,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,且点F为对角线BD的中点.所以对角线AC经过点F.又在△P AC中,点E为PC的中点,所以EF为△P AC的中位线,所以EF∥P A.又P A⊂平面P AD,EF⊄平面P AD,所以EF∥平面P AD.(2)存在满足要求的点G.在线段CD上存在一点G为CD的中点,使得平面EFG⊥平面PDC.因为底面ABCD是边长为a的正方形,所以CD⊥AD.又侧面P AD⊥底面ABCD,CD⊂平面ABCD,侧面P AD∩平面ABCD=AD,所以CD⊥平面P AD.又EF∥平面P AD,所以CD⊥EF.取CD中点G,连接FG,EG.因为F为BD中点,所以FG∥AD.又CD⊥AD,所以FG⊥CD,又FG∩EF=F,所以CD⊥平面EFG,又CD⊂平面PDC,所以平面EFG⊥平面PDC.(2019·长沙模拟)如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的2倍,P为侧棱SD上的点.(1)求证:AC⊥SD;(2)若SD⊥平面P AC,则侧棱SC上是否存在一点E,使得BE∥平面P AC?若存在,求SE∶EC;若不存在,请说明理由.[证明](1)连接BD,设AC交BD于点O,连接SO,由题意得四棱锥S-ABCD 是正四棱锥,所以SO⊥AC.在正方形ABCD中,AC⊥BD,又SO∩BD=O,所以AC⊥平面SBD.因为SD⊂平面SBD,所以AC⊥SD.(2)在棱SC上存在一点E,使得BE∥平面P AC.连接OP.设正方形ABCD的边长为a,则SC=SD=2a.由SD⊥平面P AC得SD⊥PC,易求得PD=2a 4.故可在SP上取一点N,使得PN=PD.过点N作PC的平行线与SC交于点E,连接BE,BN,在△BDN中,易得BN∥PO.又因为NE∥PC,NE⊂平面BNE,BN⊂平面BNE,BN∩NE=N,PO⊂平面P AC,PC⊂平面P AC,PO∩PC=P,所以平面BEN∥平面P AC,所以BE∥平面P AC.因为SN∶NP=2∶1,所以SE∶EC=2∶1.[大题增分专训]1.(2019·济南模拟)如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AD∥BC,AB=BC=12AD,E,F分别为线段AD,PB的中点.(1)证明:PD∥平面CEF;(2)若PE⊥平面ABCD,PE=AB=2,求三棱锥P-DEF的体积.[解](1)证明:连接BE,BD,BD交CE于点O,连接OF(图略).∵E为线段AD的中点,AD∥BC,BC=12AD=ED,∴BC ED,∴四边形BCDE为平行四边形,∴O为BD的中点,又F是BP的中点,∴OF∥PD.又OF⊂平面CEF,PD⊄平面CEF,∴PD∥平面CEF.(2)由(1)知,BE=CD.∵四边形ABCD为等腰梯形,AB=BC=12AD,∴AB=AE=BE,∴三角形ABE是等边三角形,∴∠DAB=π3,过B作BH⊥AD于点H(图略),则BH= 3.∵PE⊥平面ABCD,PE⊂平面P AD,∴平面P AD⊥平面ABCD,又平面P AD∩平面ABCD=AD,BH⊥AD,BH⊂平面ABCD,∴BH ⊥平面P AD ,∴点B 到平面P AD 的距离为BH = 3.又F 为线段PB 的中点,∴点F 到平面P AD 的距离h 等于点B 到平面P AD的距离的一半,即h =32,又S △PDE =12PE ·DE =2,∴V 三棱锥P -DEF =13S △PDE ×h =13×2×32=33.2.(2019·石家庄模拟)如图,已知四棱锥P -ABCD ,底面ABCD 为正方形,且P A ⊥底面ABCD ,过AB 的平面ABFE 与侧面PCD 的交线为EF ,且满足S △PEF :S 四边形CDEF =1∶3.(1)证明:PB ∥平面ACE ;(2)当P A =2AD =2时,求点F 到平面ACE 的距离.[解] (1)证明:由题知四边形ABCD 为正方形,∴AB ∥CD ,∵CD ⊂平面PCD ,AB ⊄平面PCD ,∴AB ∥平面PCD .又AB⊂平面ABFE,平面ABFE∩平面PCD=EF,∴EF∥AB,∴EF∥CD.由S△PEF∶S四边形CDEF=1∶3知E,F分别为PD,PC的中点.如图,连接BD交AC于点G,则G为BD的中点,连接EG,则EG∥PB.又EG⊂平面ACE,PB⊄平面ACE,∴PB∥平面ACE.(2)∵P A=2,AD=AB=1,∴AC=2,AE=12PD=52,∵P A⊥平面ABCD,∴CD⊥P A,又CD⊥AD,AD∩P A=A,∴CD⊥平面P AD,∴CD⊥PD.在Rt△CDE中,CE=CD2+DE2=3 2.在△ACE中,由余弦定理知cos∠AEC=AE2+CE2-AC22AE·CE=55,∴sin∠AEC=255,∴S△ACE=12·AE·CE·sin∠AEC=34.设点F 到平面ACE 的距离为h ,连接AF ,则V F -ACE =13×34×h =14h . ∵DG ⊥AC ,DG ⊥P A ,AC ∩P A =A ,∴DG ⊥平面P AC .∵E 为PD 的中点,∴点E 到平面ACF 的距离为12DG =24.又F 为PC 的中点,∴S △ACF =12S △ACP =22,∴V E -ACF =13×22×24=112.由V F -ACE =V E -ACF ,得14h =112,得h =13, ∴点F 到平面ACE 的距离为13.3.已知在四棱锥P -ABCD 中,平面P AB ⊥平面ABCD ,四边形ABCD 为矩形,E 为线段AD 上靠近点A 的三等分点,O 为AB 的中点,且P A =PB ,AB =23AD .(1)求证:EC ⊥PE .(2)PB 上是否存在一点F ,使得OF ∥平面PEC ?若存在,试确定点F 的位置;若不存在,请说明理由.[解] (1)证明:连接PO ,EO ,CO .∵平面P AB ⊥平面ABCD ,P A =PB ,O 为AB 的中点,∴PO⊥平面ABCD,∵CE⊂平面ABCD,∴PO⊥CE.设AD=3,∵四边形ABCD为矩形,∴CD=AB=2,BC=3,∴AE=13AD=1,∴ED=2,EC=ED2+DC2=22+22=22,OE=AO2+AE2=12+12=2,OC=OB2+BC2=12+32=10,∴OE2+EC2=OC2,∴OE⊥EC.又PO∩OE=O,∴EC⊥平面POE,又PE⊂平面POE,∴EC⊥PE.(2)PB上存在一点F,使得OF∥平面PEC,且F为PB的三等分点(靠近点B).证明如下:取BC的三等分点M(靠近点C),连接AM,易知AE MC,∴四边形AECM 为平行四边形,∴AM∥EC.取BM的中点N,连接ON,∴ON∥AM,∴ON∥EC.∵N为BM的中点,∴N为BC的三等分点(靠近点B).∵F为PB的三等分点(靠近点B),连接OF,NF,∴NF∥PC,又ON∩NF=N,EC∩PC=C,∴平面ONF∥平面PEC,∴OF∥平面PEC.。
不规则几何体体积的求法

不规则几何体体积的求法当所给几何体形状不规则时,无法直接利用体积公式求解,可尝试用以下几种常用的方法求出原几何体的体积,下面逐一介绍,供同学们参考.一、等积转换法当所给几何体的体积不能直接套用公式或套用公式时某一量(底面积或高)不易求出时,可以转换一下几何体中有关元素的相对位置进行计算求解,该方法尤其适用于求三棱锥的体积.例1在边长为a的正方体ABCD—A1B1C1D1中,M,N,P分别是棱A1B1,A1D1,A1A上的点,且满足A1M = 12A1B1,A1N=2ND1,A1P= 34A1A(如图1),试求三棱锥A1—MNP的体积.分析:若用公式V= 13Sh直接计算三棱锥A1—MNP的体积,则需要求出△MNP的面积和该三棱锥的高,这两者显然都不易求出,但若将三棱锥A1—MNP的顶点和底面转换一下,变为求三棱锥P—A1MN的体积,便能很容易的求出其高和底面△A1MN的面积,从而代入公式求解.解:V A1-MNP =V A1—MNP = 13·S△A1MN·h =13×12·A1M1·A1N·A1P=13×12×12a·23a·34a=124a3.评注:转换顶点和底面是求三棱锥体积的一种常用方法,也是以后学习求点到平面距离的一个理论依据.二、分割法分割法也是体积计算中的一种常用方法,在求一些不规则的几何体的体积以及求两个几何体的体积之比时经常要用到分割法.例2如图2,在三棱柱ABC—A1B1C1中,E,F分别为AB,AC的中点,平面EB1C1F 将三棱柱分成两部分,求这两部分的体积之比.分析:截面EB1C1F将三棱柱分成两部分,一部分是三棱台AEF—A1B1C1;另一部分是一个不规则几何体,其体积可以利用棱柱的体积减去棱台的体积求得.解:设棱柱的底面积为S,高为h,其体积V=Sh.则三角形AEF的面积为14S.由于V AEF -A 1B 1C 1=13 ·h ·(s 4 +S+s 2 )= 712Sh , 则剩余不规则几何体的体积为V ́́′=V -V AEF -A 1B 1C 1=Sh -712 Sh = 512Sh , 所以两部分的体积之比为V AEF -A 1B 1C 1:V ́́′=7:5.评注:在求一个几何体被分成的两部分体积之比时,若有一部分为不规则几何体,则可用整个几何体的体积减去规则几何体的体积求出其体积,再进行计算.三、补形法某些空间几何体是某一个几何体的一部分,在解题时,把这个几何体通过“补形”补成完整的几何体或置于一个更熟悉的几何体中,巧妙地破解空间几何体的体积问题,这是一种重要的解题策略——补形法.常见的补形法有对称补形、联系补形与还原补形.对于还原补形,主要涉及台体中“还台为锥”问题.例3 已知某几何体的三视图如图所示,则该几何体的体积为______.分析:由三视图画出直观图,补一个大小相同的几何体,构成一个圆柱即可求其体积. 解:由三视图可知,此几何体是底面半径为1,高为4的圆柱被从母线的中点处截去了圆柱的14,根据对称性,可补全此圆柱如图,故体积V =34×π×12×4=3π. 评注:“对称”是数学中的一种重要关系,在解决空间几何体中的问题时善于发现对称关系对空间想象能力的提高很有帮助.。
等积转换法

等积转换法例1:如图,ABCD 是正方形,EDGF 是长方形,CD=6厘米,DG=8厘米,求宽ED=?F AB C D E86思维点拨:连接AG ,三角形ADG 的面积等于长方形面积的一半,同时也等于正方形面积的一半。
模仿练习如图,在四边形ABCD 中,DCFG 为正方形,ABED 为梯形,DE=12厘米,DG=8厘米,AB=24厘米,求梯形ABED 的面积例2: 如图,梯形上底AB 长是18厘米,三角形ABD 的面积是198平方厘米,三角形COD 的面积比三角形AOB 的面积多66平方厘米,求梯形ABCD 的面积。
AD CBO思维点拨:因为三角形ABD 和三角形ABC 同底等高,所以三角形ABD 的面积等于三角形ABC 相等。
模仿练习如图,ABCD 是边长为4分米的正方形,长方形DEFG 的长是5分米,求长方形DEFG 的宽。
FAED C B G 是多少?例3:已知大正方形的边长是5厘米,小正方形的边长是4厘米,求阴影部分的面积。
A BD思维点拨:连接AC ,三角形GEA 和三角形GEC 同底等高。
模仿练习如图,在三角形ABC 中,BD=2DC ,AE=BE ,已知三角形ABC 的面积是18平方厘米,求四边形ACDE 的面积。
(提示:连接AC )AB D EC例4: 长方形ADEF 的面积是16平方厘米,三角形ADB 的面积是3平方厘米,三角形ACF 的面积是4平方厘米,求三角形ABC 的面积。
A DB E CF思维点拨:连接AE ,求出三角形BCE 的面积是非常关键的一步。
模仿练习如图,ABCD 、CEFG 都是正方形,AB=8厘米,CE=6厘米,求图中阴影部分的面积。
AB例5: 如图,已知四边形ABCD 被它的两条对角线分成四个三角形,其中甲的面积是1,乙的面积是2,丙的面积是3,求丁的面积。
AB C D E 甲丁乙丙思维点拨:可以利用蝴蝶原理解决,甲×丙=丁×乙。
蝴蝶原理:任意的一个四边形,两对角线连接,相对的两块面积乘积相等。
求不规则图形面积的几种方法

求不规则图形面积的几种方法作者:白福花来源:《内蒙古教育·基教版》2012年第03期摘要:初三学习弧长及扇形的面积,在计算阴影部分的面积过程中,常遇到一些平面不规则图形的面积计算问题,对这类试题由于图形的不规则使学生在求解时往往感到茫然,不知所措;然而这类试题又能开发学生智力,能体现对数学思想方法、思维能力素质的考查,本文将结合具体实例谈谈把不规则图形的面积计算问题通过变动图形的位置或对图形进行适当的分割、拼补、旋转等方法,转化成规则图形面积的计算问题。
关键词:不规则图形面积求法一、割补法割补法是求解平面不规则图形面积问题最常用的方法之一,它包含三个方面的内容:一是分割原有图形成规则图形;二是粘补原有图形为规则图形;三是分割粘补兼而有之。
例1:当汽车在雨中行驶时,为了看清楚道路,司机要启动前方挡风玻璃上的雨刷器。
如图1-1是某汽车的一个雨刷器的示意图,雨刷器杆AB与雨刷器CD在B处固定连接(不能转动),当杆AB绕A点转动90°时,雨刷CD扫过的面积是多少呢?小明仔细观察了雨刷器的转动情况量得CD=80cm,∠DBA=20°,端点C、D与点A的距离分别是115cm、35cm,他经过认真思考只选用了其中的部分数据就求得了结果,你知道小明是怎样计算的吗?也请你算一算雨刷CD扫过的面积 ______cm2 (π取3.14)略解,由于CD和AB在点B处固定连接(不能转动),所以在整个运动过程中,就有AC=AC′=115cm,AD=AD′=35cm,CD=CD′=80cm,因此△ACD≌△AC′D′,把△AC′D′割下,粘补到△ACD的位置(图1-2),则雨刷CD扫过的面积,就等于以A为圆心,AC、AD为半径的两个圆的面积差。
注:在应用割补法求解问题时,往往要综合应用“分割”与“粘补”两种技能方法兼用,对思维的灵活性和严密性有着较高的要求。
二、重叠法重叠法是将所求的图形看成是两个或两个以上图形的重叠部分,然后运用“容斥原理”解决的一种方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等积转换法
【知识与方法】
在平面几何图形中,我们往往可以根据同底等高、等底同高、等底等高等等发现面积相等的图形,这些图形有的形状相同,有的形状不同,但既然面积与面积之间具有相等关系,我们就可以相应地进行一些转化,从而使问题解决起来更加简便。
【例题精讲】
例1:如图,ABCD 是边长为4分米的正方形,长方形DEFG 的长是5分米,求长方形DEFG 的宽。
F A
E
D
C B G
思维点拨:连接AG ,三角形ADG 的面积等于长方形面积的一半,同时也等于正方形面积的一半。
模仿练习
如图,ABCD 是正方形,EDGF 是长方形,CD=6厘米,DG=8厘米,求宽ED=?
F A
B G
C
D E
86
例2: 如图,梯形上底AB 长是18厘米,三角形ABD 的面积是198平方厘米,三角形COD 的面积比三角形AOB 的面积多66平方厘米,求梯形ABCD 的面积。
A
D C
B
O
思维点拨:因为三角形ABD 和三角形ABC 同底等高,所以三角形ABD 的面积等于三角形ABC 相等。
模仿练习
如图,在四边形ABCD 中,DCFG 为正方形,ABED 为梯形,DE=12厘米,DG=8厘米,AB=24厘米,求梯形ABED 的面积是多少?
例3:已知大正方形的边长是5厘米,小正方形的边长是4厘米,求阴影部分的面积。
A B
思维点拨:连接AC ,三角形GEA 和三角形GEC 同底等高。
模仿练习
如图,ABCD 、CEFG 都是正方形,AB=8厘米,CE=6厘米,求图中阴影部分的面积。
A B
例4: 长方形ADEF 的面积是16平方厘米,三角形ADB 的面积是3平方厘米,三角形ACF 的面积是4平方厘米,求三角形ABC 的面积。
A D
B E C
F
思维点拨:连接AE ,求出三角形BCE 的面积是非常关键的一步。
模仿练习
如图,在三角形ABC 中,BD=2DC ,AE=BE ,已知三角形ABC 的面积是18平方厘米,求四边形ACDE 的面积。
(提示:连接AC )
A
B D E
C
例5: 如图,已知四边形ABCD 被它的两条对角线分成四个三角形,其中甲的面积是1,乙的面积是2,丙的面积是3,求丁的面积。
A
B C D E 甲
丁
乙丙
思维点拨:可以利用蝴蝶原理解决,甲×丙=丁×乙。
蝴蝶原理:任意的一个四边形,两对角线连接,相对的两块面积乘积相等。
模仿练习
两条对角线把梯形ABCD 分割成四个三角形,已知两个三角形的面积,求另两个三角形的面积。
A
B C D O 48
【 巩 固 与 提 高 】
A 级
1、如图,ABCD 、CEFG 都是正方形,AB=10厘米,CE=8厘米,求图中阴影部分的面积。
A B
2、如图,已知四边形ABCD 、CEFG 都是正方形,正方形ABCD 的边长是10厘米,求图中阴影部分的面积。
A
B F
3、如图,已知四边形ABCD 、CEFG 都是正方形,CE 的长度是30分米,求图中阴影部分的面积。
A B
E F
4、如图,BC=3BE ,CF=3AF ,已知三角形ABC 的面积是6平方厘米,求三角形FEC 的面积。
C A
B E F
5、如图,ABCD 是长方形,AC=7.2厘米,AB=5厘米,CDEF 是平行四边形,如果BH 长是3厘米,求图中阴影部分的面积。
A
B E
B 级
1、如图,已知长方形的长是15厘米,宽是8厘米,四边形EFGH 的面积是12平方厘米,求空白部分的面积。
A B C
2、如图,长方形ABCD 的面积是40平方厘米,三角形ADF 的面积是10平方厘米,三角形ABE 的面积是14平方厘米,求三角形AEF 的面积。
A
D
F
3、如图所示,求梯形ABCD 的面积。
A
B C D O
612
4、已知三角形AOB 的面积是15平方厘米,线段OB 的长度是OD 的3倍,求梯形ABCD 的面积。
A
B C D O
5、如图,BO=2DO ,阴影部分的面积是8平方厘米,那么求梯形ABCD 的面积。
B C
C 级 1、如图,ABC
D 、CEFG 都是正方形,AB 长是5厘米,求图中阴影部分的面积。
A B E
2、如图,长方形的长是8厘米,宽是6厘米,四边形EFGH 的面积是3平方厘米,求阴影部分的面积。
A B C D
3、如图,已知OC=2AO ,三角形BOC 的面积是20平方厘米,求梯形的面积。
4、如图,阴影部分的面积是6平方厘米,OC=2AO ,求梯形的面积。
B C
5、如下图,在三角形ABC 中, BC =8厘米, AD =6厘米,E 、F 分别为AB 和AC 的中点.那么三角形EBF 的面积是______平方厘米
.。
