用加减消元法解方程组
5.2-加减消元法解二元一次方程组

6 7y 9 7y 96 7y 3 3 y 7
联系上面的解法,想一想怎样解方程组
3x 5 y 21 2 x 5 y 11
① + ②
① ②
异加
4x 5 y 3 2 x 5 y 1
① - ②
①
② 同减
3x 5 y 21 2 x 5 y -11
6x-5y=17②
1. 用加减法解方程组
应用(B )
A.①-②消去y B.①-②消去x C. ②- ①消去常数项 D. 以上都不对
3x+2y=13
2.方程组
3x-2y=5
消去y后所得的方程是(B )
A.6x=8 B.6x=18 C.6x=5 D.x=18
三、指出下列方程组求解过程中有错误步骤, 并给予订正: 7x-4y=4 ①
加减法
(4)
9x-5y=1 6x-7y=2
加减法
⑴ 如果方程组的两个方程中某一未知数的系数相等或者 互为相反数时,把两个方程的两边分别 相减或相加 , 消去一个未知数,得到一元一次方程,解这个方程得一 个未知数的值。将求得的未知数代入其中一个方程得另 一个未知数的值,从而解得方程组的解。同减异加 ⑵如果方程组中某一未知数系数绝对值均不相等时,把 一个或两个方程两边 乘以一个适当的数 , 使两个方程 中某一未知数的系数绝对值相等,从而化为上述类型方 程组求解。 特别的,当一个方程中某未知数的系数是另一个方程同 一未知数的系数 的倍数时 ,加减消元法比较合适。
(口算或在草稿纸上进行笔算),即把求得的解代入 每一个方程看是否成立.
1、根据等式性质填空: <1>若a=b,那么a±c= b±c ( .等式性质1) 思考:若a=b,c=d,那么a+c=b+d吗? <2>若a=b,那么ac= bc . (等式性质2)
用加减消元法解二元一次方程组练习题

是通常的加法和乘法运算,已知 3*5=15,4*7=28,则 a+b=
.
6.将方程 1 x+2y=1 中的 x 项的系数化为 2,则下列结果中正确的是( ) 3
A、2x+6y=1 B、2x+2y=6 C、2x+6y=3 D、2x+12y=6
7.某校课外小组的学生准备分组外出活动,若每组 7 人,则余下 3 人;若每组 8 人,则最后一组只有 3 人,设课外小组的人数为 x,分成的组数为 y.依题意
2x+3y=6 ②
(2)
5x-5y=7 ① 15x+20y=7 ②
10.已知代数式 x2+bx+c,当 x=-3 时,它的值为 9,当 x=2 时,它的值为 14,当 x=-8 时,求代数式的值。
11.若∣m+n-5∣+(2m+3n-5)2=0,求(m+n)2 的值
12.甲、乙两个小马虎,在练习解方程组
可得方程组为( )
A、 7y=x+3 B、 8y+5=x
7x+3=y 8ቤተ መጻሕፍቲ ባይዱ-5=y
C、 7y=x-3 8y=x+5
D、 7y=x+3 8y=x+5
8.用代入法解下列方程组: (1) y=x+6 ①
2x+3y=8 ②
2x+3y=-19 ① x+5y=1 ②(2)
9.用加减法解下列方程组: (1) 2x+5y=12 ①
了方程组中的 a,得到方程组的解为 x=1
程组的解为
y=6
问原方程组的解为多少?
ax+y=10 x+by=7 时,由于粗心,甲看错 ;乙看错了方程组中的 b,得到方
x=-1 y=12
用加减消元法解二元一次方程组练习题
1.用代入法解方程组3xx8yy
3(1) 14(2)
由①可得
.
加减消元法

加减消元法加减消元法是代数中的一种运算方法,常用于解决方程组。
它的思想是通过加减操作,消除未知数,从而求得方程组的解。
下面我们将详细介绍加减消元法的基本原理和应用。
加减消元法的基本原理是利用方程的等价性质,在方程组中进行加减操作,使得其中的某一未知数系数为0。
假设我们有一个由n个方程和n个未知数构成的方程组,可以表示为:a₁₁x₁ + a₁₂x₂ + ... + a₁ₙxₙ = b₁a₂₁x₁ + a₂₂x₂ + ... + a₂ₙxₙ = b₂...aₙ₁x₁ + aₙ₂x₂ + ... + aₙₙxₙ = bₙ其中,aᵢⱼ表示系数矩阵中第i行第j列的元素,xᵢ表示未知数,bᵢ表示常数项。
通过加减操作,我们可以将第j个方程的m倍加到第i个方程上,从而将第i个方程中的第j个未知数系数消除。
具体的操作可以表示为:aᵢⱼ' = aᵢⱼ - maₙₙbᵢ' = bᵢ - mbₙ其中,aᵢⱼ'表示新的第i行第j列的系数,bᵢ'表示新的常数项。
通过这样的操作,我们可以得到一个新的方程组。
经过一系列的加减操作,我们可以将方程组化简为一个上三角形矩阵形式:a₁₁x₁ + a₁₂x₂ + ... + a₁ₙxₙ = b₁...............aₙₙ₋₁xₙ₋₁ + aₙₙxₙ = bₙ'其中,bₙ'为消元后的常数项。
接下来,我们可以利用回代的方式求解未知数。
从最后一行开始,可以得到最后一个未知数的值,然后依次往上求得其他未知数的值。
具体的操作可以表示为:xₙ = bₙ' / aₙₙxₙ₋₁ = (bₙ₋₁ - aₙₙ₋₁xₙ) / aₙₙ₋₁...x₁ = (b₁ - a₁₂x₂ - ... - a₁ₙxₙ) / a₁₁通过这样的操作,我们可以得到方程组的解。
加减消元法在实际应用中十分常见。
例如,在线性方程组求解、线性回归、最小二乘法等问题中,都可以使用加减消元法来求解问题。
消元—解二元一次方程组(加减消元法)教学设计与反思
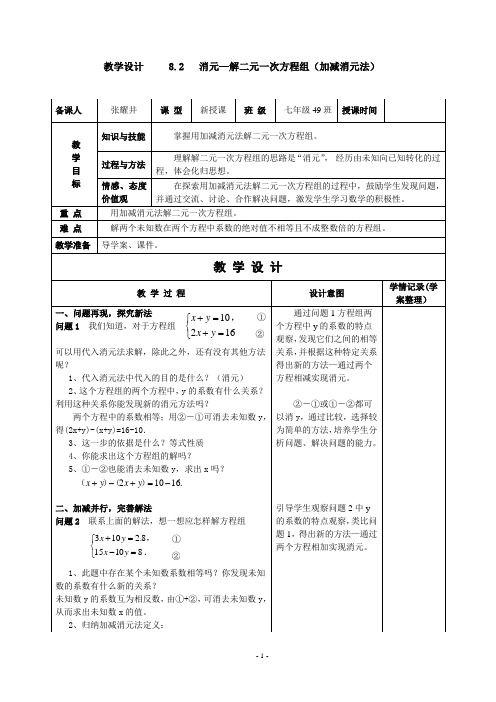
教学设计 8.2 消元—解二元一次方程组(加减消元法)
教学反思:
“解二元一次方程组”是“二元一次方程组”一章中很重要的知识,占有重要的地位。
通过本节课的教学,使学生会用加减消元法解二元一次方程组,进一步了解“消元”的思想。
加减法解二元一次方程组的基本思想与代入法相同,仍是“消元”化归思想,通过代入法、加减法这些手段,使二元方程转化为一元方程,从而使“消元”化归这一转化思想得以实现。
因此在设计教学过程时,注重化归意识的点拨与渗透,使学生在学习中逐步体会理解这种具有普遍意义的分析问题、解决问题的思想方法。
在小组展示中,学生说出自己的思路,展示过程中,我仅用极少的时间进行点拨,引导学生学习重点知识,进行追问。
如:“(1)-(2)的目的什么?”“(1)×3,(2)×5的目的是什么”“解决本道题重要的一步是什么?”“这么好的办法,你是怎么想到的?”
教学后发现,大部分学生能够通过加减消元法解二元一次方程组,教学一开始给出了一个二元一次方程组,先让学生用代入法求解,既复习了旧知识,又引出了新课题,引发学生探究的兴趣。
通过学生的观察、发现,理解加减消元法的原理和方法,使学生明确使用加减法的条件,体会在一定条件下使用加减法的优越性。
之后,通过两个例题来帮助学生规范书写,同时明确用加减法解二元一次方程组的步骤。
接下来,通过一系列的练习来巩固加减消元法的应用,并在练习中摸索运算技巧,培养能力,训练学生思维的灵活性及分析问题、解决问题的综合能力。
有个别同学在运算上比较容易出错,运用的灵活性掌握得不太好,解答起来速度较慢,我想只要多加练习,一定会又快又准确的。
二元一次方程的加减消元法

二元一次方程的加减消元法二元一次方程组是指含有两个未知数的一次方程组,一般形式为:ax + by = c.dx + ey = f.加减消元法是解二元一次方程组的一种常用方法。
它的基本思想是通过加减操作消去一个未知数,从而将方程组化简为只含有一个未知数的方程,然后求解得到另一个未知数的值。
具体步骤如下:1. 将方程组中的两个方程按照形式对齐,确保同类项在一起。
2. 通过加减操作消去一个未知数。
可以通过乘以适当的系数使得两个方程中同类项的系数相等,然后相加或相减消去一个未知数。
3. 化简得到只含有一个未知数的方程。
4. 求解得到一个未知数的值。
5. 将求得的未知数的值代入原方程组中的一个方程,求解得到另一个未知数的值。
举例说明:考虑方程组:2x + 3y = 8。
3x 2y = 1。
首先将两个方程按照形式对齐:2x + 3y = 8。
3x 2y = 1。
然后通过加减操作消去一个未知数:将第一个方程乘以3,第二个方程乘以2,得到:6x + 9y = 24。
6x 4y = 2。
相减得到:13y = 22。
化简得到只含有一个未知数的方程:y = 22/13。
将y的值代入原方程组的第一个方程中,求解得到x的值: 2x + 3 (22/13) = 8。
2x + 66/13 = 8。
2x = 8 66/13。
2x = 34/13。
x = 17/13。
因此,通过加减消元法,可以求得方程组的解x=17/13,y=22/13。
总之,加减消元法是解二元一次方程组的一种有效方法,通过适当的加减操作可以简化方程组,从而求得未知数的值。
加减消元法10个例题

加减消元法10个例题加减消元法是解决一元二次方程或多元线性方程组的一种常用方法。
它的基本思想是通过加减方程,消除一个或多个未知数,得到一个简化的方程,从而求解未知数的值。
下面是10个应用加减消元法解决问题的例题。
1. 求解方程组:2x + 3y = 84x - 5y = 17通过将第二个方程乘以2,然后与第一个方程相加,可以消除x 的项,从而得到一个只含有y的方程。
2. 求解方程组:3x - 4y = 57x + 2y = -13通过将第一个方程乘以7,第二个方程乘以3,然后相减,可以消除x的项,从而得到一个只含有y的方程。
3. 求解方程组:x + y + z = 62x - 3y + 4z = 93x - 2y - z = 4通过适当加减方程,可以消除其中一个未知数的项,从而得到一个只含有两个未知数的方程组。
4. 求解方程组:x - y + z = 22x + y - 3z = -4-3x + 2y + 5z = 12通过适当加减方程,可以消除其中一个未知数的项,从而得到一个只含有两个未知数的方程组。
5. 求解方程:x^2 + 3x - 10 = 0可以通过将方程两边同时加上一个适当的数,从而消除一次项,得到一个二次方程。
6. 求解方程:2x^2 + 5x - 3 = 0可以通过将方程两边同时减去一个适当的数,从而消除一次项,得到一个二次方程。
7. 求解方程:3x^2 - 2x + 1 = 0可以通过将方程两边同时乘以一个适当的数,从而消除二次项,得到一个一次方程。
8. 求解方程:4x^2 - 9 = 0可以通过将方程两边同时开方,从而消除二次项,得到一个一次方程。
9. 求解方程:x^3 + 2x^2 - 5x + 6 = 0可以通过将方程两边同时加上一个适当的多项式,从而消除一次项和二次项,得到一个一次方程。
10. 求解方程:(x + 1)^2 - (2x - 3)^2 = 0可以通过将方程两边展开,然后合并同类项,从而消除二次项,得到一个一次方程。
7.2.2 加减消元法解二元一次方程组

所以m=13, 所以x+y=13, 解得x=-13,
n=-1,
x-y=-1, y=23.即 Nhomakorabea方程组的解为
x=-13,
y=23.
14 已知实数 m,n 满足 m+n=5,且98mm++89nn==2120k,-13, 求 k 的值. 三名同学分别提出了以下三种不同的解题思路: 甲同学:先解关于 m,n 的方程组 98mm++89nn==2120k,-13,再求 k 的值.
【答案】 D
10 若3xm+2n y8与-2x2y 3m+4n是同类项,则m-n的值为 ___5___.
【点拨】 由题意得m3m++2n4n==2,8,解得mn==-4,1, 则 m-n=4-(-1)=5.
11 已知方程组23xx+ -125y+y-203= =00,的解也是关于 x,y 的方 程 ax+y=4 的一个解,求 a 的值. 解:解方程组23xx+-125y+y-230==00,,得xy==1-,6,
将xy==1-6,代入 ax+y=4,
得-6a+1=4,解得 a=-12.
12 已知关于 x,y 的二元一次方程组xx+-yy==35m-+m3. , (1)若 x,y 互为相反数,求 m 的值;
解:若x,y互为相反数,则x+y=0, 所以3m+3=0,解得m=-1.
(2)若x是y的2倍,求原方程组的解.
将 x=5 代入①,得 10-3y=-2,解得 y=4.
所以方程组的解为xy==45.,
3x-2y=5, (2)y+3x=11.
解:3y+x-3x2=y=115.,②①②-①,得 3y=6,解得 y=2. 将 y=2 代入①,得 3x-2×2=5,解得 x=3. 所以原方程组的解是xy==23.,
二元一次方程组的加减消元法

二元一次方程组的加减消元法加减消元法是指当二元一次方程组的两个方程中同一个未知数的系数互为相反数或者相等时,把这两个方程的的两边分别进行相加或相减运算,就能消去这个未知数,从而得到一个一元一次方程。
加减消元法解二元一次方程组的解题步骤:
一、变形:根据绝对值较小的未知数(相同未知数)的系数的最小公倍数,将方程的两边都乘适当的数,使两个方程的某一个未知数的系数相等或互为相反数,然后通过加减法消去这个未知数。
特别提醒:选择消元对象时最好选择未知数的系数互为相反数、相等、倍数关系或者是互为质数的未知数作为消元对象。
二、加减:两个方程中同一个未知数的系数互为相反数时,将两个方程直接相加;同一个未知数的系数相等时,将两个方程相减,从而消去一个未知数,将二元一次方程组转化为一元一次方程。
特别注意:两个方程相加减时,一定要把两个方程等号两边分别相加减,且要注意各项符号的变化。
三、求解:解消元后的一元一次方程,求出另外一个未知数的值。
四、回代:把求得未知数的值,回代到方程组中较简单的一个方程,从而求出另外一个未知数的值。
五、写解:把两个未知数的值用大括号联立起来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.2 消元——加减消元法解二元一次方程组(第1课时)
一、学习目标
1. 进一步体会解二元一次方程组的基本思想——消元思想。
2. 能理解、运用加减消元法解简单的二元一次方程组。
3. 培养阅读课本的方法,提高自学能力。
二、 温故知新:
1. 根据等式性质填空:
<1>若a =b ,那么a ±c = . (等式性质1)
<2>若a =b ,那么ac = . (等式性质2)
<3>思考:若a =b ,c =d ,那么a ±c =b ±d 吗?
2.用代入法解方程的关键是什么?
3.之前我们用什么方法解过下面这个方程组?
⎩⎨⎧=+=+40
222y x y x
具体步骤是:由①得 =y . ③,把③代入①得 .从而达到消元的目的。
(即把二元一次方程变成我们较熟悉的一元一次方程)
三、学习内容:
(一)提出问题,阅读课本,得出加减法的定义。
1. 解这个方程组⎩⎨⎧=+=+40
222y x y x 除了用代入法,还有别的方法吗?
2.
请大家认真阅读课本99面第二个思考前的内容。
回答第一个思考中的问题。
3.探讨:课本上的这半句话:“②-①可消去y ,得 x =18”中隐含了那些步骤? 4. 思考:联系上面的解法,想一想应怎样解方程组⎩⎨⎧=-=+.
81015,6.3104y x y x 5.总结得出加减法的定义。
初一( )班 号 姓名
2.填空题。
(1)已知方程组⎩⎨⎧=-=+6
32173y x y x 两个方程只要两边 就可以消去未知数 。
(2)已知方程组⎩⎨⎧=+=-10
62516725y x y x 两个方程只要两边 就可以消去未知数 。
3.选择题。
(1)用加减法解方程组⎩⎨⎧=--=+1756
76y x y x 应用 ( )
A.①-②消去y.
B.①-②消去x.
C. ②-①消去常数项.
D. 以上都不对. (2)方程组⎩⎨⎧=-=+5231323y x y x 消去y 后所得的方程是
A.6x =8.
B.6x =18.
C.6x =5.
D.x =18.
(三)例题分析。
例3.用加减法解方程组
⎩⎨⎧=-=+336516
43y x y x
解:
(四)练习。
1.用加减法解下列方程组。
⎩⎨⎧=+=+5238
52)1(y x y x ⎩⎨⎧-=-=+2
236
32)2(y x y x
四、小结。
五、布置作业。
P 103 习题8.2第3大题。
