第二章控制系统的数学模型习题及答案
《控制工程基础》课程作业习题(含解答)
第一章概论本章要求学生了解控制系统的基本概念、研究对象及任务,了解系统的信息传递、反馈和反馈控制的概念及控制系统的分类,开环控制与闭环控制的区别;闭环控制系统的基本原理和组成环节。
学会将简单系统原理图抽象成职能方块图。
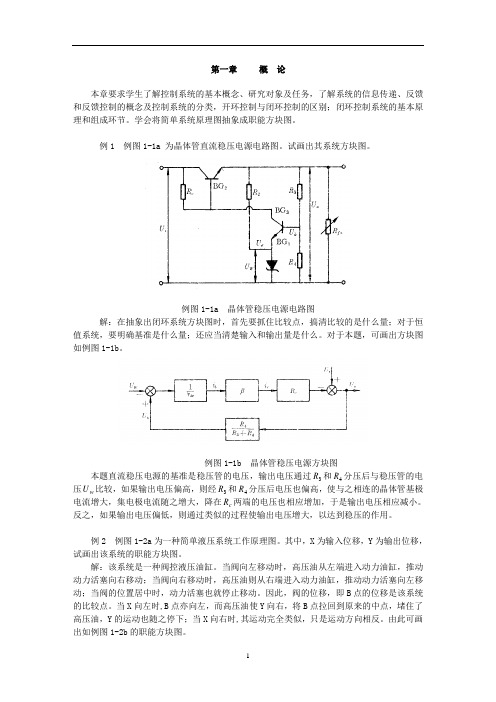
例1 例图1-1a 为晶体管直流稳压电源电路图。
试画出其系统方块图。
例图1-1a 晶体管稳压电源电路图解:在抽象出闭环系统方块图时,首先要抓住比较点,搞清比较的是什么量;对于恒值系统,要明确基准是什么量;还应当清楚输入和输出量是什么。
对于本题,可画出方块图如例图1-1b。
例图1-1b 晶体管稳压电源方块图本题直流稳压电源的基准是稳压管的电压,输出电压通过R和4R分压后与稳压管的电3压U比较,如果输出电压偏高,则经3R和4R分压后电压也偏高,使与之相连的晶体管基极w电流增大,集电极电流随之增大,降在R两端的电压也相应增加,于是输出电压相应减小。
c反之,如果输出电压偏低,则通过类似的过程使输出电压增大,以达到稳压的作用。
例2 例图1-2a为一种简单液压系统工作原理图。
其中,X为输入位移,Y为输出位移,试画出该系统的职能方块图。
解:该系统是一种阀控液压油缸。
当阀向左移动时,高压油从左端进入动力油缸,推动动力活塞向右移动;当阀向右移动时,高压油则从右端进入动力油缸,推动动力活塞向左移动;当阀的位置居中时,动力活塞也就停止移动。
因此,阀的位移,即B点的位移是该系统的比较点。
当X向左时,B点亦向左,而高压油使Y向右,将B点拉回到原来的中点,堵住了高压油,Y的运动也随之停下;当X向右时,其运动完全类似,只是运动方向相反。
由此可画出如例图1-2b的职能方块图。
例图1-2a 简单液压系统例图1-2b 职能方块图1.在给出的几种答案里,选择出正确的答案。
(1)以同等精度元件组成的开环系统和闭环系统,其精度比较为_______ (A )开环高; (B )闭环高; (C )相差不多; (D )一样高。
(2)系统的输出信号对控制作用的影响 (A )开环有; (B )闭环有; (C )都没有; (D )都有。
第二章控制系统的数学模型例题全

L ddt
Ac ost
L
Asint
A 2 S2
2
另一种解法:
设xt Acost, xs A s
s2 2
x0 Acost A t0
Lddt xt sx(s) x0
Lddt Acost
s s2
s
2
A
A 2
S2 2
7已知f t cost- cos2t,求Fs。 8已知f t 2e-tsin2t,求Fs。 9已知f t te-2t ,求Fs。 10已知f t t n ,求Fs。
dt
2已知Fs
ss
4
2
, 求f
t
。
3已知Fs 1 ,求f 0、f 。
sa
3已知Fs 1 ,求f 0、f 。
sa
f 0
lims Fs s
lims s
s
1 a
1
f
lims s0
s
1 a
0
• Using the laplace transform methodes solve the differential equations
第二章控制系统的数学模型 例题
1已知f t d Acost,求Fs。
dt
2已知f t 3t 4e2t ,求Fs。
3已知f t e3tsin4t,求Fs。
t
4已知f t Acostdt,求Fs。
0
5已知f t sint ,求Fs。
6已知f t 8e-100t - 5e-200t ,求Fs。
G1
-1
- G2
N1
C
G2
C 1 G 2 G 3
N1 1 G 2 G1G 2G3
自动控制原理C作业(第二章)答案
4 3
0.1
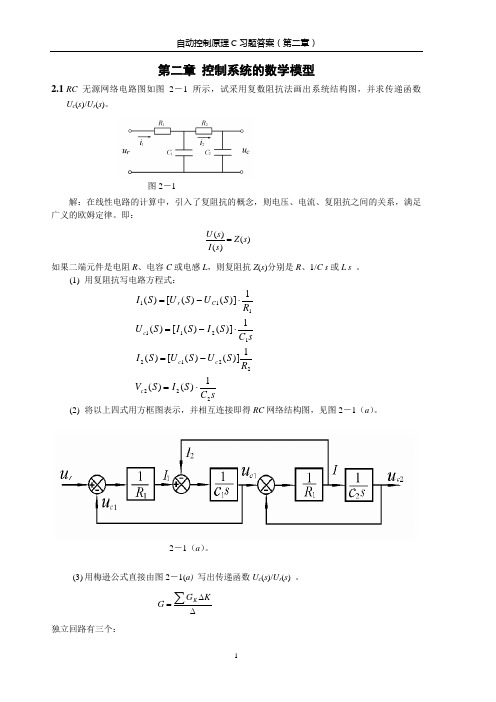
图 3-1 二阶控制系统的单位阶跃响应
解 在单位阶跃作用下响应的稳态值为 3,故此系统的增益不是 1,而是 3。系统模型为
(s)
s2
3
2 n
2n s
2 n
然后由响应的 p % 、 t p 及相应公式,即可换算出 、 n 。
p%
c(t p ) c() c()
4
3
3
33%
t p 0.1(s)
P1 G1G2
1 1
P2 G2G4
2 1
因此,传递函数为
C(s) P11 P2 2
R(s)
G2G1 G4G2 1 G1G2G3
3
自动控制原理 C 习题答案(第二章)
2.4 用梅森公式求系统传递函数。
R(S)
-
_
+ G1(s)
- _
G2(s)
+ C(S)
+
图 2-4 解: 单独回路 5 个,即
L1
1 R
1 C1S
1 R1C1S
11
1
L2
R2
C2S
R2C2 S
L3
1 C1S
1 R2
1 R2C1S
回路相互不接触的情况只有 L1 和 L2 两个回路。则
L12
L1L2
1 R1C1R2C2S 2
由上式可写出特征式为:
1
( L1
L2
L3 )
L1 L2
1
1 R1C1S
1 R2C2 S
1 R2C1S
1 R1C1R2C2S 2
益 K1 和速度反馈系数 Kt 。同时,确定在此 K1 和 Kt 数值下系统的延迟时间、上升时间和调节时间。
第二章 控制系统的数学模型习题及答案

第二章 控制系统的数学模型习题及答案2-1 试建立下图所示各系统的微分方程。
其中电压)(t u r 和位移)(t x 为输入量;电压)(t u c 和位移)(t y 为输出量;R (电阻),C (电容),k (弹性系数),和f (阻尼系数),均为常数。
解:(a )应用复数阻抗概念可写出)()(11)(11s U s I csR cs R s U c r ++= (1) 2)()(R s Uc s I =(2) 联立式(1)、(2),可解得:CsR R R R Cs R R s U s U r c 212112)1()()(+++=微分方程为:r r c c u CR dt du u R CR R R dt du 121211+=++ (b )如图解2-1(b)所示,取A,B 两点分别进行受力分析。
对A 点有 )()(111dtdydt dx f x x k -=- (1) 对B 点有 y k dtdydt dx f 21)(=- (2) 联立式(1)、(2)可得:dtdx k k k y k k f k k dt dy2112121)(+=++ 2-2 试证明下图所示的力学系统(a)和电路系统(b)是相似系统(即有相同形式的数学模型)。
解:(a) 取A 、B 两点分别进行受力分析,如图解所示。
对A 点有)()()(1122y y f y xf y x k -=-+- (1) 对B 点有1111)(y k y yf =- (2) 对式(1)、(2)分别取拉氏变换,消去中间变量1y ,整理后得)()(s X s Y = 21212121221212212121()1()1f f f fs s k k k k f f f f f s s k k k k k +++++++21221221221211221221k k s )k f k f k f (s f f k k s )k f k f (s f f +++++++= (b) 由图可写出sC R s U c 221)(+= sC R s C R sC R s U r 111112111)(+⋅++整理得)()(s U s U r c = 1)(1)(21221122121221122121+++++++s C R C R C R s C C R R s C R C R s C C R R 比较两系统的传递函数,如果设112211221,1,,,R k R k C f C f ====则两系统的传递函数相同,所以两系统是相似的。
第二章控制系统的数学模型

第二章控制系统的数学模型§2.1引言●数学模型(1)描述系统输入、输出变量及内部各变量关系的数学表达式。
I—O—内部变量(2)系统中各物理量之间相互作用的关系及各自的变化规律用数学形式表达出来。
(3)是舍弃了各种事物的具体特点而抽象出它们的共同性质(即运动)来加以研究的工具。
●控制理论研究的问题是:(1)一个给定的控制系统,它的运动有何性质和特性—分析* 运动:泛指一切物理量随时间的变化(2)怎样设计一个控制系统,使其运动具有给定的性质和特性—综合和设计●工程角度上:控制理论要解决的问题(进一步解释)(1)不满足于求解方程c(t)=f(r(t) )—数学课程已有(2)提出更深入的问题a.这些曲线有何共同性质;b.系统参数值波动对曲线有何影响?c.如何修改参数甚至结构才能改进这些曲线,使之满足工程要求。
—建立控制系统的数学模型,也是研究和解决这些问题的第一步,故建立描述控制系统运动的数学模型是控制理论的基础。
数学模型的形式不只一种:它们各有特长和最适合的场合;它们彼此之间也有紧密的联系;各种数学描述方法的共同基础是微分方程;一元高次微分方程多元一次微分方程(状态方程)Laplace变换为工具——传函传函阵§ 2.2 基本数学模型例 用数学模型表示下图的RC 无源网络给定r u 为输入量,c u 为输出量解:由克希霍夫定律 ⎰+⋅=idt i R u C r 1 r c c u u dtdu RC =+ ⎰=idt u C c 1 令T RC =(时间参数),则微分方程为:r c c u u dtdu T =+ 线性定常系统在初始条件为零时,传递函数为:£{c(t)}/£{r(t)})()()(s U s U s U s T r c c =+⋅⋅ 1.1)(/)()(+==→s T s U s U s G r c 其形式和参数由系统的结构和参数决定,与r(t)无关。
第二章控制系统数学模型

有极限存在。
终值定理在分析研究系统的稳态性能时(例如分析系统的稳态误差,求取系统
输出量的稳态值等)有着很多的应用。因此终值定理也是一个经常用到的运算
定理。
7.初值定理: lim f (t) lim sF (s)
18
2
例2-1:写出RLC串联电路的微分方程。
ui
L
R
i
C
uo
ui 输入
uo 输出
[解]:据基尔霍夫电路定理:
L di dt
Ri
1 C
idt
ui
①
uo
1 C
idt
②
由②: i C d,uo代入①得: dt
LC
d 2uo dt 2
RC
duo dt
uo
ui
这是一个线性定常二阶微分方程。
3
例2-2 设一弹簧、质量块、阻尼器组成的系统如图所示,当外力 F(t)作用于系统时,系统将产生运动。试写出外力F(t)与质量块的 位移y(t)之间的微分方程。
uR uc Us
把 uR i R
和
ic
C
duc dt
代入电路,可得到电路的
微分方程:
RC
duc dt
uc
Us
23
现在对于上面的微分方程,我们用Laplace变换求解。
首先,利用Laplace变换中的微分定理,将微分方程变换成如下形式:
RC
duc dt
uc
Us
RCsU c (s) Uc (s) Us R(s)
利用待定系数法可求得:
A 1 ARC B 0
F (s) L[ f (t)] f (t)e st dt 0
第二章 控制系统的数学模型

= Ur (s)
传递函数为: di + u ur= R · + L i c dt Uc (s) 1 = duc G (s) = i = C dt Ur (s) LCs2 + RCs + 1
电气系统三要素:电阻、电容、电感
+ ί(t) R –
u(t)= ί(t)· R
u (t )
ί(t) C
–
u(t) ί(t)= R
图2-9 速度控制系统
+
R1 R2 R2 R1 k2
ui
R1
k1 u 1
c
u2
功 ua 放
m
SM
ω
负 载
ut
TG
运算放大器
uu+ ii+
_ +
+
Add
uo
差模输入电压等于零
u+= u-
运放同相输入端与反向输入端两点的电压相等,如同该 两点短路一样,称为虚短。
i+=i-=0
运放同相输入端与反向输入端的电流都等于零,如同该 两点被断开一样,称为虚断。
Tm s m ( s ) m (t ) K1U a ( s )
Tm s 1 m ( s) K1U a ( s)
m ( s) K1 G ( s) U a ( s) Tm s 1
m ( s) K2 G ( s) M c ( s) Tm s 1
传递函数的性质(续)
(5)传递函数与微分方程有相通性;
b1s b2 C (s) G ( s) R( s ) a0 s 2 a1s a2
对角线相乘
a0 s 2 a1s a2 C ( s ) b1s b2 R ( s )
第2章 控制系统的数学模型 参考答案
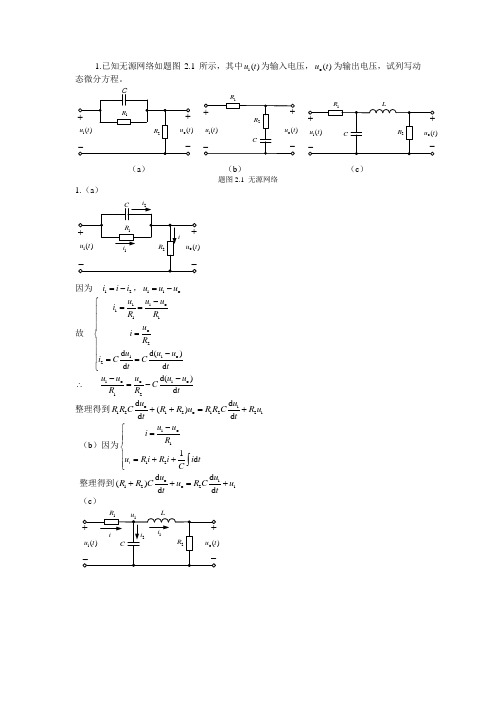
1.已知无源网络如题图2.1所示,其中i ()u t 为输入电压,o ()u t 为输出电压,试列写动态微分方程。
(a ) (b ) (c )题图2.1 无源网络1.(a )因为 12i i i =-,1i o u u u =-故 i o 1111o2i o 12d()d d d u u u i R R u i R u u ui C Ct t -⎧==⎪⎪⎪=⎨⎪⎪-==⎪⎩i o o i o 12d()d u u u u u CR R t--∴=- 整理得到o i 1212o 122i d d ()d d u uR R C R R u R R C R u t t++=+(b )因为i o 1121d i uu i R u R i R i i t C -⎧=⎪⎪⎨⎪=++⎪⎩⎰整理得到o i 12o 2i d d ()d d u uR R C u R C u t t++=+(c )因为i 1121o 1122o 1o 2()d d d d u u i i i i R u u i i C R t u L u u R t ⎧-=+=⎪⎪⎪⎪==⎨⎪⎪-=⎪⎪⎩得到oi 1112o 1o2()d d d d u u u u C R R t u L u u R t -⎧=+⎪⎪⎨⎪=+⎪⎩2o o oo o i 2111222d d d d d d u u u u u u L CL C R R R R t R t R t --=++ 整理得到2o o 11212o 2i 2d d ()()d d u uR LC R R C L R R u R u t t++++=2.试求题图2.2中各无源网络的传递函数。
)(a ) (b ))C(c ) (d )题图2.2 习题2的无源网络2. (a )因为111111R Z R Cs R Cs ==+ 所以o 2122i 121212()()()U s R R R Cs R G s U s Z R R R Cs R R +===+++ (b )因为11111111R Z R C s R C s ==+,22222211R C s Z R C s C s +=+= 所以o 211222i 121212112212()(1)(1)()()()1U s Z R C s R C s G s U s Z Z R R C C s R C R C R C s ++===+++++ (c )因为()()()22122221111R Ls R Ls Cs Z R Ls Cs LCs R Cs R Ls Cs++=+==++++ 所以o 122i 1111212()()()()U s Z Ls R G s U s R Z R LCs R R C L s R R +===+++++ (d )因为1212112111211()1R R C s R Z R R C s R C s R C s +=+=++,32232211R C s Z R C s C s+=+=所以2o 3121211213222i 121223131211212232()()()1()()()()1U s R R R C C s R C R C R C s Z G s U s Z Z R R R R R R C C s R C R C R C R C s +++++===++++++++ 3. 试求题图2.3中各有源网络的传递函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章控制系统的数学模型习题及答案2-1 试建立下图所示各系统的微分方程。
其中电压u r(t)和位移x(t)为输入量;电压u c(t)和位移y(t)为输出量;R (电阻),C (电容),k (弹性系数),和f (阻尼系数),均为解:(a)应用复数阻抗概念可写出R i丄U r(s) c il(s) U c (s)R i cs(i )I(s)Uc(s)R2(2)2-2 试证明下图所示的力学系统(a)和电路系统(b)是相似系统(即有相同形式的数学模型)联立式(I)、(2),可解得:U c(s) R2(i R i Cs)U r (s) R i R2 R i R2CS微分方程为du c R R2du r1"dT CRR2Uc IT cR1Ur(b)如图解2-1(b)所示,取A,B两点分别进行受力分析。
对A点有k i(x x i) dy) (i)对B点有k2y (2)联立式(1)、(2)可得:dy k i k? k i dxdt f (k i k2)y k i k2 dt上1(蛊_尙)A B解:(a)取A 、B 两点分别进行受力分析,如图解所示。
对A 点有k 2(x y)f 2(x y)f i (y y i ) (1)对B 点有f i ( y y i ) k i y i(2)对式(i )、(2)分别取拉氏变换,消去中间变量 y i ,整理后得(b)由图可写出U c (s)整理得如果设R i k i ,R 2 i k 2,C i f i ,C 2 f 2,则两系统的传递函数相同,所以两系统是相似的。
U c (s)。
U r (s)Y(s) 口2s 2 I f f " k i k ?k i k ?(一 -)s i f i f 2s 2(f i k 2 f 2k i)sk ikX(s)(f if k ik 2护1f 2k if 2k 2)s k ikU r (s)R 2iC 2sR ii C i S i C isU c (s) U r (s)R iR 2C iC 2s 2(R i C iR 2C 2)s i2R iR 2C iC 2s(R i CiR 2C 2R-i C 2)s i比较两系统的传递函数,2-3 求下图所示各有源网络的传递函数(f i k 2位脉冲响应和传递函数。
解: c(0) 1,c(0) 0时,由 c(t) 3c(t) 2c(t) 2r(t)得 2s C(s) sc(0)c(0) 3sC(s) 3c(0) 2C(s)2R(s) 代入初始条件得:2〜、2 s 3s142C(s)s(s 1)(s 2) s s 1 s 2c(t) /鼻t2t1 4e 2e解: U c (s) U?(s)(b ) U c (s) R 2 C 2s (1R 1 C 1s)(1 R 2C 2s)U r (s)R 1 R 11 C 1s 1 C 1sR 1 C 2s(a)根据运算放大器“虚地”概念,可写出 1 (c) U c (s) R 2 C ~Cs R 2 *Cs R 2U r (s)R 1&(1 R 2CS )2-4 已知在零初始条件下,系统的单位阶跃响应为 c(t) 1c 2t2ee t ,试求系统的单k(t) ■dc 也4e 2tdt(s)L[k(t)]3s 2 (s 1)(s 2)2-5系统传递函数C 廻 R(s) __ 2_s 23s试求初始条件为c(0) c(0) 0时系统在输入r(t)1(t)作用下的输出 c(t)。
2-6 飞机俯仰角控制系统结构图如图所示,试求闭环传递函数 Q c (S )Q,S )。
Q c (s)32Q r (s) s (0.90.7K)s (1.18 0.42K)s|亘]里曹叵]―叵]——-ri>—利用结构图等效化简或梅逊增益公式可求出系统的闭环传递函数为C(s)G22G 3G 4R(s) 1 G 2G 3G 6 G 3G 4G 5G 1G 2G 3G 4G 7 G 1G 2G 3G 4G 82-8试用结构图等效变换法化简下图所示系统,并求各系统的传递函数 解:(a )川:1 *G 毘 + 641 GSg皿G盹)|r-解: 经结构图等效变换可得闭环系统的传递函数0.7(s 0.6) 0.68 2-7 已知系统方程组如下,试绘制系统结构图,并求闭环传递函数X i (s) X 2(s) X 3(s) C(s)G i (s)R(s) G i (s)G(s) G 8(S )]C(S )G 2(S )[X"S ) G 6(S )X 3(S )][X 2(s) C(s)G 5(s)]G 3(s) G 4(s)X 3(s)C(s) ----- oR(s)解:系统结构图如下:C(s) R(s)°C(s) G22G 3G 4R (s) 1 G 1G 2 G 3 G 4 G 2G 3G 1G 2G 3G 4C (s)G 1G 2G 3所以:旦「R(s) 1 G 1G 2 G 2 G 3 G 1G 2G 32-9试用梅逊增益公式求下图中各系统的闭环传递函数。
解:(a )图中有1条前向通路,4个回路P 1 G 1G 2G 3G 4, 11L 1G 2G 3H 1, L 2 G 1G 2G 3H 3, L 3 G 1G 2G 3G 4HL 4G 3G 4H 2,1 (L 1 L2 L3 L 4)C(s) P 1 1G 1G 2G 3G 4R(s)1 G 2G 3 H 1 G 1G 2G 3H 3 G 1G2 G 3G 4 H 4 G 3G 4H 2(b )图中有4条前向通路,5个回路P 1G 1, P 2 G 1G 2, P 3G 2, P 4G 2G 1,L 1G -i ,L 2G 1G 2, L 3G 2,L 4G 2G 1, L 5G 1G 2,1 2341,1 (L 1 L2 L3 L 4),(b )=■1-<LM所以:C(s) G 1 G 2 R(s) 1 G 2H(c )=r-1 +口眄恥:,「aGf|U ;U 5 t — 4- C^j0^0-^所以:C(s) P1 1 P2 2 P3 3 P4 4G1G1G 2G 2G 2G12G1G 2G1G2 1 G1G1G 2G 2G 2G1G1G 2 1 G1G2 3G1G 2(c)图中有2条前向通路,3个回路,有1对互不接触回路P1 G1G2G3, 1 1, P2 G4G3 ,2 1L1,L1G1G 2H -i,L 2 G 3H 2,L 3G 2 H3 :1 1 (L1 L2 L3 ) L 1L 2,C(s)P1 1 P2 2 G1G 2G 3G 4G3 (1 G 1G2H1)R(s) 1 G1G 2H1G3H2 G2H3 G1G 2G3H1H2-10已知系统的结构图如下,图中R(s)为输入信号,N(s)为干扰信号,试求总输出C(s)。
令N(s) 0,求C©。
图中有2条前向通路,3个回路,有1对互不接触回路。
R(s)则有令R(s)P3C(s) N(s)C(s)2 1 L11 G2H,L1 G2H,L2G1G 2, L 3G1G 3,1 (L1 L2 L3) L1L3,C(s) P1 1 P2 2 G1G 2 G1G3 (1 G 2 H)R(s) 1 G 2H G1G 2G1G 3G1G 2G 3H0,求C(s) 。
有3条前向通路,回路不变。
N(s)P1 1, 1 1 L1,P2 G4G1G2, 2 1iP1 G1G2, 1 P2 G1G3,G 4G 1G3,P1 1L i,(L1 L2 L3) L1L3,P3 G 4G 1G 3(1 G 2 H)R( s)[G 1G 2 GG(11 G 2H G 4G1G 21 G 2H G1G 2G1G 3G1G 2G 3HG2H)] N(s)[ 1 G2H G 4G1G 2 G 4G 1G 3 (1 G 2H )] 1 G 2H G1G 2 G 1G 3 G 1G 2G 3H解:(a)(b )令 N,s)0 N 2(S ) 0,求C(s)。
图中有R(s)1条前向通路,1个回路。
P 1笃,11, L 12K(s s 21) 1 L 1,则有C(s)P 11KsR(S )(2K 1)s 2(K1)令 R(s) 0, N 2 (s),求 C(s)N 1(S ) 。
图中有 1条前向通路,回路不变。
P 1 s ,11,则有C(S ) P 1 1s(s 2)N 1(S )(2K 1)s 2(K1)令 R(s) 0, N 1 (S ),求-C(s) 。
图中有 1条前向通路,回路不变。
N 2(S )竺,11则有 3 L2K S 2N 2(S )(2K 1)S 2(K1)ksR(s) s(s 2)2 (s) 2kN 2(s)(2k 1)s 2(k1)(c ) 令 N(s)0,求C(s) R(S )。
图中有 3条前向通路,2个回路。
P 1G 2G 4,11 , P 2G 3G 4,21 ,P 3 G 1G 2G 4 ,31,L 1G 2G 4,L 2 G 3G4,1J L 2),则有C(s)P 1 1 P 22P 3 3G 2G 4G 3G 4G 1G 2G 4R(S )1 G 2G 4 G 3G 4令R(s) 0 ,求-C^。
有1条前向通路,回路不变。
N(S )11,则有匸廻日_二LN (S )1 G 2G 4 G 3G 4R (S )[G 2G 4 G 3G 4 G 1G 2G 4] N (S )G 42-1 1P 1 G 4,C(s)1 G 2G 4G 3G 4Y G l(1 6H3)G4G3H3H2HG R1 G1H1G3H3 G1G2G3H1H2H 3G1H1G3H3。
