第三章-基本波函数.docx
波函数

结论: 结论:3)波函数所代表的波是几率波. 波函数所代表的波是几率波. 微观粒子出现在|Ψ 大的地方, Ψ 微观粒子出现在 Ψ|2大的地方,|Ψ|2小的 地方粒子出现少;粒子受波数所引导, 地方粒子出现少;粒子受波数所引导, 波函数按波的形式去分配粒子的出现的 几率. 几率. 例)求一个能量为E,动量为 的自由粒子的几率 求一个能量为 ,动量为P的自由粒子的几率 i 密度. 密度. ( EtPr ) 解: 波函数为 Ψ = Ψ e 0
∞→∞
因为粒子在全空间出现是必然事件
例1: 设粒子在一维空间运动,其状态可用波函 : 设粒子在一维空间运动, 数描述为: 数描述为:
ψ ( x, t ) = 0
( x ≤ b / 2), x ≤ b / 2)
其中A为任意常数, 和 均为确定的常数. 均为确定的常数 其中 为任意常数,E和b均为确定的常数. 为任意常数 归一化的波函数;几率密度W? 求:归一化的波函数;几率密度W? 解:由归一化条件,有: 由归一化条件,
nπ 其最大值对应于 sin = ±1 4
L 2 2 nπ ω n = Ψ ( ) = sin 4 L 4
,于是有: 于是有:
∴ n = 2(2k + 1)
π nπ = ( 2k + 1) (k = 0,1,2, ) 4 2
(k = 0,1,2, )
�
cos (
2
πx
b
)dx = 1
b ∴ A =1 2
2
∴ A =
2 b
由此可求出归一化的波函数和几率密度 几率密度为: 几率密度为:
W ( x, t ) = ψ 2 ( x, t ) = 0 ( x ≤ b / 2), x ≤ b / 2) 2 2 π x 2 W ( x, t ) = ψ ( x, t ) = cos ( ) ( b / 2 ≤ x ≤ b / 2) b b
波函数公式
波函数公式:y=A0cos[w(t-x/u)+A)。
波函数是量子力学中描写微观系统状态的函数。
在经典力学中,用质点的位置和动量(或速度)来描写宏观质点的状态,这是质点状态的经典描述方式,它突出了质点的粒子性。
量子力学(Quantum Mechanics),为物理学理论,是研究物质世界微观粒子运动规律的物理学分支,主要研究原子、分子、凝聚态物质,以及原子核和基本粒子的结构、性质的基础理论。
它与相对论一起构成现代物理学的理论基础。
量子力学不仅是现代物理学的基础理论之一,而且在化学等学科和许多近代技术中得到广泛应用。
大学物理波函数

18
例1:已知描述粒子的归一化波函数为(t,x,y,z),求在t时刻、 在x到x+dx的无限大薄层内发现粒子的概率。
( t,x ,y ,z ) d x d y d z 解: 体积元内的概率为
Ψ
2
7
4.用电子双缝衍射实验说明概率波的含义 先看经典波: 声波的干涉
振幅矢量相加
i t A ( x ) e 通过上缝的声波用 描述 1 it )e 描述 2(x 通过下缝的声波用 A
A A ) e 双缝 齐开时的声波为 ( 1 2
i t
8
A A ) e 双缝 齐开时的声波为 ( 1 2
薛定谔方程
§15-1 §15-2 §15-3 §15-4 波函数及其统计诠释 薛定谔方程 力学量的算符表示和平均值 一维势阱和势垒问题
1
波函数的统计解释 一、波函数和概率波
二、物理对波函数的要求
三、自由粒子的波函数
2
一、波函数和概率波
1. 波函数
物质波波函数写成 ( r ,t )
2.玻恩(M.Born)假设 物质波不代表实在物理量的波动 而是刻划粒子在空间概率分布的概率波
10
•双缝齐开时 电子可通过上缝 也可通过下缝 通过上 下缝各有一定的概率 总概率幅
Ψ Ψ Ψ 12 1 2
2 12 2 2
21
| Ψ | | Ψ Ψ | 总概率密度 P 12 1
2 1 2 2
12
出现了干涉
干涉项
11
结论 1)干涉是概率波的干涉 是由于概率幅的线性叠加产生的 2)即使只有一个电子 当双缝齐开时
归一化条件
( r , t ) ( r , t ) d 1
波函数及薛定谔方程详解课件

03ቤተ መጻሕፍቲ ባይዱ
CATALOGUE
薛定谔方程在量子力学中的应用
无限深势阱
无限深势阱模型描述粒子被限 制在一定空间范围内运动的情 形,通常用于描述微观粒子在
势能无限高区域的行为。
在无限深势阱中,波函数具有 特定的边界条件,即在势阱边
界处波函数为零。
薛定谔方程在无限深势阱中的 解为分段函数,表示粒子在不 同势阱内的能量状态。
波函数及薛定 谔 方程详解课件
contents
目录
• 波函数简介 • 薛定谔方程概述 • 薛定谔方程在量子力学中的应用 • 波函数与薛定谔方程的关系 • 实验验证与实例分析 • 总结与展望
01
CATALOGUE
波函数简介
波函数的定 义
波函数是一种描述微观粒子状 态的函数,它包含了粒子在空 间中的位置和动量的信息。
06
CATALOGUE
总结与展望
波函数与薛定谔方程的意义
波函数
波函数是描述微观粒子状态的函数, 它包含了粒子在空间中的位置、动量 和自旋等所有信息。通过波函数,我 们可以计算出粒子在给定条件下的行 为和性质。
薛定谔方程
薛定谔方程是描述波函数随时间变化 的偏微分方程,它反映了微观粒子在 运动过程中所遵循的规律。通过求解 薛定谔方程,我们可以预测粒子在不 同条件下的行为和性质。
时间相关形式
在有限域中,薛定谔方程的形式为 ifrac{dpsi}{dt}=Hpsi,其中H为哈密 顿算子。
薛定谔方程的解
分离变量法
对于具有周期性势能的情况,可以将波函数分离为几个独立的函数,分别求解 后再组合得到原方程的解。
微扰法
对于势能存在微小扰动的情况,可以通过微扰法求解薛定谔方程,得到近似解。
大学物理波函数

P2
2 a
sin
2
2π a
x
3
E3 9E1
3
2 sin 3π x aa
P3
2 a
sin
2
3π a
x
46
一维无限深方势阱中粒子的波函数和概率密度
电子的相干性注意差别之处10电子的状态用波函数描述?只开上缝时电子有一定的概率通过上缝其状态用描述?只开下缝时电子有一定的概率通过下缝其状态用描述111212干涉项总概率密度电子可通过上缝也可通过下缝通过上下缝各有一定的概率121干涉是概率波的干涉是由于概率幅的线性叠加产生的2即使只有一个电子两部分概率幅的叠加就会产生干涉3微观粒子的波动性实质上就是概率幅的相干叠加性它的状态也要用来描述结论13经典声波干涉项干涉项物质波电子双缝齐开时总的概率幅为1212振幅概率幅14波函数统计诠释量子力学中描述微观粒子的波函数本身是没有直接物理意义的具有直接物理意义的是波函数的模的平方它代表了粒子出现的概率
概率密度为 (x, y, z, t) (x, y, z, t) (x, y, z, t)
波函数是单值的、连续的和有限的。
波函数 (r,t)和A (r,t) (A是常数)描述了同一个量子 态,对于空间任意两点 ri 和 rj 有
(ri ,t) 2
(rj
,
t
)
2
写成
i
t
2 2m
2 x 2
•令上述关系作用于波函数 (x,t)
•得到自由粒子满足的薛定谔方程
i (x,t) 2 2 (x, t)
t
2m x2
23
3. 有势场中粒子的薛定谔方程
第三章波动方程

2 t2V p 2 2 2 t2V p 2divg r(a t)d
▪ 将点震源用半径r=a的小球代替,小球体积为W。对上式 求体积分,并令r->0,其极限情况就是点震源的达朗贝 尔解。
lr i0m W2 t2 dW Vp2lr i0m Wdivgd raW dlr i0m W(t)dW
▪ 各种算子在球坐标系中的表达式为:
u 1u 1 u
gradru errersine
对于球面u只 纵存 波 r方在 , 向位 上 u只 移 , (是 r,t)的 即函数 u, u0 则
u rer u rrr
拉普拉斯算子:
2u
1 r2
r
(r2
ur )r
s1in(sin1r u
)r29;1(tV rp)rr
➢ 2、近震源的球面纵波( 1/r2 >> 1/r)
1
rr
up4r2Vp 2 1(tVp)r
26
3.3 地震波的动力学特点
▪ 在近震源区域,质点振动规律(波 函数)主要与震源函数 (t)有关;而 在远震源区域,质点振动主要与震 源函数的导数 '(t)有关。
2u
2
u u 0
1 r2
(2r
ur2 r
2u r2 )
2u 2
r2
r
u r
15
3.2 无限大、均匀各向同性介质中的球面波
将各种算子带入纵波的波动传播方程,得到著名的弦方程:
2 t21V P 2 2 r210
1r
可用达朗贝尔法 解r得:c(tr )c(tr )
1
第三章 基本波函数
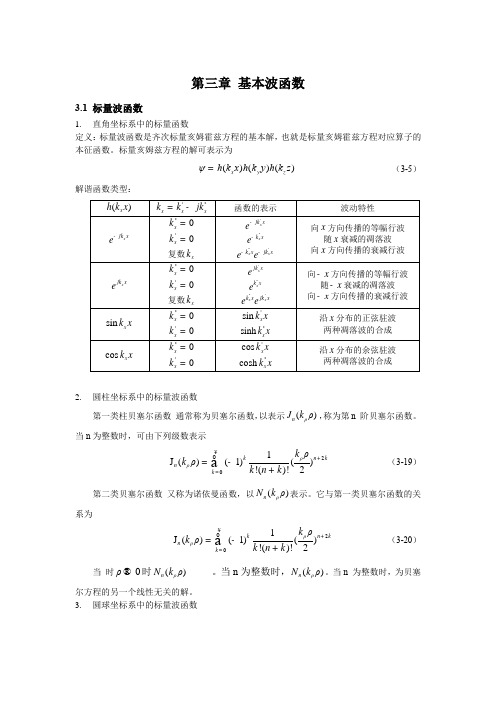
第三章基本波函数3.1 标量波函数1. 直角坐标系中的标量函数 定义:标量波函数是齐次标量亥姆霍兹方程的基本解,也就是标量亥姆霍兹方程对应算子的本征函数。
标量亥姆兹方程的解可表示为()()()x y z ψh k x h k y h k z =(3-5)解谐函数类型:2. 圆柱坐标系中的标量波函数第一类柱贝塞尔函数通常称为贝塞尔函数,以表示()n ρJ k ρ,称为第n 阶贝塞尔函数。
当n 为整数时,可由下列级数表示201J ()(1)()!()!2ρkn k n ρk k ρk ρk n k ¥+==-+å(3-19) 第二类贝塞尔函数又称为诺依曼函数,以()n ρN k ρ表示。
它与第一类贝塞尔函数的关系为201J ()(1)()!()!2ρkn k n ρk k ρk ρk n k ¥+==-+å(3-20)当时0ρ®时()n ρN k ρ 。
当n 为整数时,()n ρN k ρ。
当n 为整数时,为贝塞尔方程的另一个线性无关的解。
3. 圆球坐标系中的标量波函数21()(1)2!n n n n nd P x x n dx=-(3-37) 11111Q ()P ()(ln )P ()P ()21nn n k n k k xx x x x xk--=+=--å(3-38) 式(3-37)和式(3-38)分别称为第一类勒让德函数()n P x 和第二类勒让德函数Q ()n x 。
3.2平面波、柱面波和球面波用标量基本波函数展开及应用1. 平面波用圆柱面基本波函数展开向x 方向传播得平面波用柱面波基本波函数展开为()jkxn jn φn n ej J k ρe ¥--=-?=å(3-47)2. 柱面波用基本波函数展开利用贝塞尔函数的叠加定理,以'ρ为中心轴的柱面波可转变为以Z 轴中心轴的柱面波,即''(2)'()'(2)'0'(2)()'()();Ψ()44()();jn φφn n n jn φφn n n J k ρH k ρe ρρj j H k J k ρH k ρe ρρ ¥-=-?¥-=-?ìïï<ïïï=-=íïï>ïïïîååρρ(3-50) 3. 平面波用球面波基本波函数展开cos 0(21)()(cos )jkr θn n n n ej n j kr P θ¥--==+å(3-56)4. 球面波用基本波函数展开'(2)''0(2)'0''(2)'0(21)()()(cos );4()44(21)()()(cos );4jk r r n n nn n n n n jk n h kr j kr P θr r πe jk h k πjk πn j kr h kr P θr r π ¥--=¥=ì?ï+<ïï-ï=-=íï--ï+>ïïïîåår r r r 5. 点源场的平面波展开'''()()2Ψ8x y z y xj k x x k y y k z z x y zk k jedk dk πk 轾--+-+-犏臌=蝌(3-69)3.3 理想导电圆柱对平面波的散射(2)()()s jn n zn J ka E e H ka ϕ∞=-∞=∑(3-79) 上述散射场式(3-79)中级数的收敛快慢与理想导电圆柱半径的相对大小有关。
波函数及其统计解释

动量分布概率(1)
设子设有平出 动 面pr现 量波 px在的ixip点波的y函pjr概y数j附z率k为近p如,zk的何则为概表(|粒r率示)(子r。?) 的|2eip动|r /量(x,,y, z那) |2么表粒示子粒具
任意粒子的波函数可以按此平面波做傅立叶展开
(r )
1
(2)3
2
( p)eipr / d 3 p
*
(
p)
p
(
p)d
3
p
p
*
(r )
pˆ
(r )d
3r
,
pˆ
力学量用算符表示
A
*
(r )
Aˆ
(r )d
3r
20
三、力学量用算符表示(5)
力学量 A 的平均值为
A
*
(r )
Aˆ
(r )d
3r
其 问中 题,:Aˆ坐为标力r学的量平A均的值算符r 。
*
(r )r
(r )d
该如何理解波函数的物理意义?为此,人们
提出了波函数的统计诠释来作为对波函数物
理意义的一种理解。
4
量子力学的基本假定之一
基本假定Ⅰ:波函数假定 微观粒子的状态可以被一个波函数完全 描述,从这个波函数可以得出体系的所 有性质。波函数一般满足连续性、有限 性和单值性三个条件。 说明:波函数一般是粒子坐标和时间的 复函数,波函数的模方代表粒子空间分 布的概率密度。
量子力学
波函数及其统计解释 粒子的动量分布 不确定度关系——进一步讨论
1
简短回顾
1、自由粒子的波函数 既然粒子具有波动性,那么就应该用一
个反映波动的函数来加以描述。 由平面波公式 Asin(kxt)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章基本波函数
3.1标量波函数
1. 直角坐标系中的标量函数
定义:标量波函数是齐次标量亥姆霍兹方程的基本解,也就是标量亥姆霍兹方程对应算子的 本征函数。
标量亥姆兹方程的解可表示为
2. 圆柱坐标系中的标量波函数
笫一类柱贝塞尔函数通常称为贝塞尔函数,以表示Jgp),称为第n 阶贝塞尔函数。
当n 为整数时,可由下列级数表示
系为
(3-20)
当吋“® 0时N n (k /)P ) o 当n 为整数时,伙/)。
当n 为整数吋,为贝 塞尔方程的另一个线性无关的解。
3. 圆球坐标系中的标量波函数
h(k x x)
k
x = J jk x
函数的表示
波动特性
向X 方向传播的等幅行波
e z
e 心
随X 衰减的凋落波 复数忍
“・ k r x - ik..x e x e y
向X 方向传播的衰减行波
e jk 'xX 向・X 方向传播的等幅行波 e ikxX
£;= 0
e k 'xX
随・兀衰减的凋落波
复数任
向・X 方向传播的衰减行波 cm If v
Q=0 sin 心 沿X 分布的正弦驻波 人 < =0
sinh kx ■A 两种凋落波的合成 nnQ u v
£;= 0 cos kx 人 沿兀分布的余弦驻波 人
< =()
cosh kx
两种凋落波的合成
屮=h(k x x)h(k v y)h(k z z)
(3-5)
・ ••
解谐函数类熨:
JJV )= i (・ i)"
A=0
] (kpP 2k
(3-19)
第二类贝塞尔函数 又称为诺依曼函数, 以Ng)表示。
它与第一类贝塞尔函数的关
式(3-37)和式(3-38)分别称为第一类勒让徳函数鬥(x)和第二类勒让徳函数Q”(x)。
3・2平面波、柱面波和球面波用标量基本波函数展开及应用
1. 平面波用圆柱面基本波函数展开
向x 方向传播得平面波用柱面波基本波函数展开为
0曲=I 厂匕(切)严
(3-47)
斤―?
2. 柱面波用基本波函数展开
利用贝塞尔函数的叠加定理,以"为屮心轴的柱面波可转变为以Z 轴屮心轴的柱面波,即
_ a J©p)H 化kp)eiWp< p
a J©p )H,、kppw,p> p
1 w=- ?
平而波用球而波基木波函数展开
0 gs 〃=彳 厂0+1)人鮒比(cos 0)
n=0
1 d n Tn\dx n (3-37)
] 1+ x QQ)")(»卜
(叽⑴
k=l K
(3-38)
(3-50)
(3-56)
3. 4.
(2〃 + 1)皆)(kr')j n (kr)P n (cos 0)\r< (2〃 + l)y ;(加)皆)(kr)P n (cos
;
5.
点源场的平面波展开
屮=
-虜(•「)+©(片站)+札卜zj
----------------------------- dk dk v
k = x y
(3-69)
3.3理想导电圆柱对平面波的散射
g s
- ______ 2Z v 丿”血)严
2
族St 比珥肋)
上述散射场式(3・79)中级数的收敛快慢与理想导电圆柱半径的相对大小有关。
3.4理想导电圆柱对柱面波的散射
OO
(3-79)
球面波用基本波函数展开
3.9 矢量波函数
电磁场满足矢量亥姆崔兹方程,为了直接求解矢量亥姆崔兹方程,需要引入矢量波函数, 矢量波函数是3个独立的矢量函数,分别用帀及币表示,其定义为
3・6 3・7
AR 侥呼(如…
理想导电劈对柱面波的散射
E 严 2E 乞 j m/2J m/2(kp) 771 = 1
理想导电圆筒上的孔隙辐射
VLe~jk 「cos (耳 cos
&) E 厂
(3-88)
sin^sin^
m m
(3-98)
oo
y
曲 1 _(竺 cos &)2 ”一 H : (ka sin 0)
2
理想导体圆球对球面波的散射
=<
半丝 £ (2〃 +1)矿)(”)丿;(肝比(cos &); 4 兀
/?=o
兰如 £ (2〃 + l)y ;(加曲(kr)P n (cos &); 5粽
r<r
(3-134) r > r 1
分层媒质上的电偶极子
3.8
反射波及透射波均可看成垂直电偶极子产生的场:
&• = Ju, Il r R(kp )HWkpP 应耐E
%7l 」
—oo
kpdkp (3-139)
反射系数和透射系数:
式屮
jujl f T(kp)H»(kpP )叮
2
P
—k p dk p
(3-140)
6*2 G + £]巧
(3-144)
(3-145)
£
(3-146)
民-kp
(3-147)
E
;
R
5
r =(1
£ = V 屮 / (3-148a)
雨= Vx(利) (3-148b)
7V = lvxVx(^ 屮、J(3-148c) k
三个矢量波函数具有以下性质:
(1)Z为无旋场;
(2)雨及帀均为无散场;
(3)L.帀及币Z间两两正交。
可以看出性质(1)和(2)是显然的,性质(3)也容易证明。
于是Z、帀及帀构成正交
函数系,且可证明是完备的。
这样Z、帀及帀的线性组合可构成矢量亥姆崔兹方程的完备解。
