勾股定理练习
(完整版)勾股定理练习题(含答案)

希望教育 勾股定理练习题1. 下列说法正确的是( )A.若 a 、b 、c 是△ABC 的三边,则a 2+b 2=c 2;B.若 a 、b 、c 是Rt△ABC 的三边,则a 2+b 2=c 2;C.若 a 、b 、c 是Rt△ABC 的三边, 90=∠A ,则a 2+b 2=c 2;D.若 a 、b 、c 是Rt△ABC 的三边, 90=∠C ,则a 2+b 2=c 2.2. Rt△ABC 的三条边长分别是a 、b 、c ,则下列各式成立的是( )A .c b a =+ B. c b a >+ C. c b a <+ D. 222c b a =+3. 如果Rt△的两直角边长分别为k 2-1,2k (k >1),那么它的斜边长是( )A 、2kB 、k+1C 、k 2-1D 、k 2+14. 已知a ,b ,c 为△ABC 三边,且满足(a 2-b 2)(a 2+b 2-c 2)=0,则它的形状为( )A.直角三角形B.等腰三角形C.等腰直角三角形D.等腰三角形或直角三角形5. 直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )A .121B .120C .90D .不能确定6. △ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为( )A .42B .32C .42 或 32D .37 或 337.※直角三角形的面积为,斜边上的中线长为,则这个三角形周长为( )S d (A(B(C ) (D)2dd 2d +d+8、在平面直角坐标系中,已知点P 的坐标是(3,4),则OP 的长为( )A :3B :4C :5D :79.若△ABC 中,AB=25cm ,AC=26cm 高AD=24,则BC 的长为( )A .17 B.3 C.17或3 D.以上都不对10.已知a 、b 、c 是三角形的三边长,如果满足则三角形的形状是( 2(6)100a -+=)A :底与边不相等的等腰三角形B :等边三角形C :钝角三角形D :直角三角形11.斜边的边长为cm 17,一条直角边长为cm 8的直角三角形的面积是 .12. 等腰三角形的腰长为13,底边长为10,则顶角的平分线为__. 13. 一个直角三角形的三边长的平方和为200,则斜边长为14.一个三角形三边之比是6:8:10,则按角分类它是 三角形.15. 一个三角形的三边之比为5∶12∶13,它的周长为60,则它的面积是__. 16. 在Rt△ABC 中,斜边AB=4,则AB 2+BC 2+AC 2=_____.17.如图,已知ABC ∆中,︒=∠90C ,15=BA ,12=AC ,以直角边BBC 为直径作半圆,则这个半圆的面积是 .18.若三角形的三个内角的比是3:2:1,最短边长为cm 1,最长边长为cm 2,则这个三角形三个角度数分别是 ,另外一边的平方是 .19. 一长方形的一边长为cm 3,面积为212cm ,那么它的一条对角线长是 .20.如图,一个高4m 、宽3m 的大门,需要在对角线的顶点间加固一个木条,求木条的长.21、有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC 沿∠CAB 的角平分线AD 折叠,使它落在斜边AB 上,且与AE 重合,你能求出CD 的长吗? 22.一个三角形三条边的长分别为cm 15,cm 20,cm 25,这个三角形最长边上的高是多少?23.如图,要修建一个育苗棚,棚高h=3m ,棚宽a=4m ,棚的长为12m ,现要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?24.如图,有一只小鸟在一棵高13m 的大树树梢上捉虫子,它的伙伴在离该树12m ,高8m 的一棵小树树梢上发出友好的叫声,它立刻以2m/s 的速度飞向小树树梢,它最短要飞多远?这只小鸟至少几秒才可能到达小树和伙伴在一起?25.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30m 处,过了2s 后,测得小汽车与车速检测仪间距离为50m ,这辆小汽车超速了吗?AE答案:一、基础达标1. 解析:利用勾股定理正确书写三角形三边关系的关键是看清谁是直角.答案: D.2. 解析:本题考察三角形的三边关系和勾股定理.答案:B.3. 解析:设另一条直角边为x ,则斜边为(x+1)利用勾股定理可得方程,可以求出x .然后再求它的周长.答案:C .4.解析:解决本题关键是要画出图形来,作图时应注意高AD 是在三角形的内部还是在三角形的外部,有两种情况,分别求解.答案:C.5. 解析: 勾股定理得到:22215817=-,另一条直角边是15,所求直角三角形面积为21158602cm ⨯⨯=.答案: 260cm .6. 解析:本题目主要是强调直角三角形中直角对的边是最长边,反过来也是成立.答案:222c b a =+,c ,直角,斜,直角.7. 解析:本题由边长之比是6:8:10 可知满足勾股定理,即是直角三角形.答案:直角.8. 解析:由三角形的内角和定理知三个角的度数,断定是直角三角形.答案:︒30、︒60、︒90,3.9. 解析:由勾股定理知道:22222291215=-=-=AC AB BC ,所以以直角边9=BC 为直径的半圆面积为10.125π.答案:10.125π.10. 解析:长方形面积长×宽,即12长×3,长4=,所以一条对角线长为5.答案:cm 5.二、综合发展11. 解析:木条长的平方=门高长的平方+门宽长的平方.答案:5m .12解析:因为222252015=+,所以这三角形是直角三角形,设最长边(斜边)上的高为xcm ,由直角三角形面积关系,可得1115202522x ⨯⨯=⨯⋅,∴12=x .答案:12cm 13.解析:透阳光最大面积是塑料薄膜的面积,需要求出它的另一边的长是多少,可以借助勾股定理求出.答案:在直角三角形中,由勾股定理可得:直角三角形的斜边长为5m,所以矩形塑料薄膜的面积是:5×20=100(m 2) .14.解析:本题的关键是构造直角三角形,利用勾股定理求斜边的值是13m ,也就是两树树梢之间的距离是13m ,两再利用时间关系式求解.答案:6.5s .15.解析:本题和14题相似,可以求出BC 的值,再利用速度等于路程除以时间后比较.BC=40米,时间是2s ,可得速度是20m/s=72km/h >70km/h .答案:这辆小汽车超速了.A 观测点。
勾股定理典型练习题(含答案)

勾股定理典型练习题(含答案)1.勾股定理典型练题勾股定理是几何中的一个重要定理。
在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载。
如图1所示,由边长相等的小正方形和直角三角形构成,可以用其面积关系验证勾股定理。
图2是由图1放入矩形内,已知AC = 4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为多少?已知AB = 3,得到∠BAC = 90°。
根据勾股定理,BC = 5.所以矩形KLMJ的面积为 4 × 5 + 3 × 4 = 32.因此,答案为C。
2.勾股定理典型练题XXX所示,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形。
若正方形A,B,C,D的边长分别是3,5,2,3,则最大正方形E的面积是多少?根据图中所示,正方形E的边长为2,所以面积为2 × 2 = 4.因此,答案为C。
3.勾股定理典型练题如图所示,在边长为4的等边三角形ABC中,AD是BC边上的高,点E,F是AD上的两点。
则图中阴影部分的面积是多少?首先,根据勾股定理,AC = 4,BC = 4,AB = 4√2.因此,三角形ABC的面积为4√2 × 4 / 2 = 8√2.由于三角形ADE和三角形ABF相似,所以ADE的面积是ABF的面积的一半。
同理,三角形BDF和三角形BCE相似,所以BDF的面积是BCE的面积的一半。
因此,阴影部分的面积为8√2 - 2 × 2 - 2 ×1 = 8√2 - 6.因此,答案为C。
4.勾股定理典型练题如图所示,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为多少?根据图中所示,正方形a和正方形c的边长分别为√5和√11.因此,正方形b的边长为√11 - √5,所以面积为(√11 - √5)² = 6.因此,答案为C。
5.勾股定理典型练题如图所示,分别以直角△ABC的三边AB、BC、CA为直径向外作半圆,设直线AB左边阴影部分面积为S1,右边阴影部分面积为S2,则S1和S2的大小关系是什么?首先,根据勾股定理,AB = √(BC² + AC²) = 2√2.因此,半圆的面积为π × (2√2 / 2)² = 2π。
勾股定理--练习题
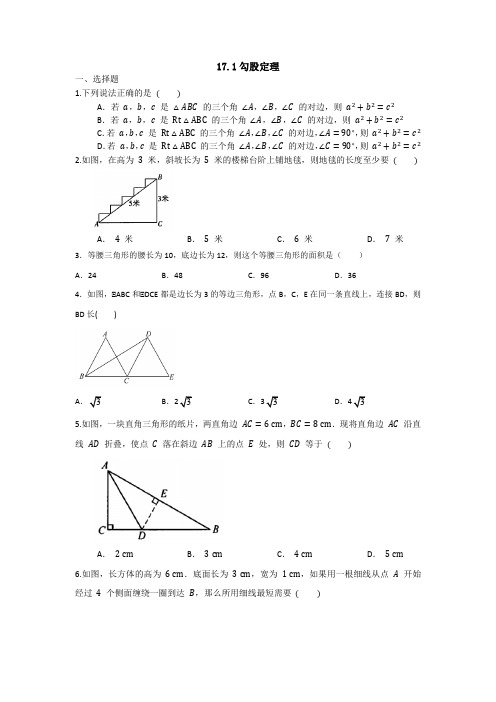
17.1勾股定理一、选择题1.下列说法正确的是( )A.若a,b,c是△ABC的三个角∠A,∠B,∠C的对边,则a2+b2=c2B.若a,b,c是Rt△ABC的三个角∠A,∠B,∠C的对边,则a2+b2=c2C.若a,b,c是Rt△ABC的三个角∠A,∠B,∠C的对边,∠A=90∘,则a2+b2=c2 D.若a,b,c是Rt△ABC的三个角∠A,∠B,∠C的对边,∠C=90∘,则a2+b2=c2 2.如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要( )A.4米B.5米C.6米D.7米3.等腰三角形的腰长为10,底边长为12,则这个等腰三角形的面积是()A.24B.48C.96D.364.如图,△ABC和△DCE都是边长为3的等边三角形,点B,C,E在同一条直线上,连接BD,则BD长()A B.C.3D.45.如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使点C落在斜边AB上的点E处,则CD等于( )A.2cm B.3cm C.4cm D.5cm6.如图,长方体的高为6cm.底面长为3cm,宽为1cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达B,那么所用细线最短需要( )A.12cm B.11cm C.10cm D.9cm7.如图,在平面直角坐标系中,点P的坐标为(-2,3),以点O为圆心,以OP为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于()A.-4和-3之间B.3和4之间C.-5和-4之间D.4和5之间二、填空题8.如图,一根竹子高10尺(3尺= 1米),折断后竹子顶端落在离竹子底端3尺处,则折断处离地面的高度是尺.9.在△ABC中,AB=AC=13,BC=10,则高AD的长是.10.如图,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD的中点,则EC=.11.如图,一架梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端的距离为0.7米;当梯子顶部A沿墙下移0.4米到Aʹ处时,梯子底部B将会外移0.8米到达Bʹ处,则梯子AB长为米.12.如图是一个三级台阶,它的每一级的长、宽、高分别为20dm,3dm,2dm.A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为dm.13.如图,△ABC中,△ACB=90°,分别以AC、BC为斜边作等腰直角三角形S1、S2,以AB为边作正方形S.若S1与S2的面积和为9,则正方形S的边长等于_______.三、解答题14.有一只小鸟在一棵高4m的小树最顶端抓虫子,它的伙伴在离该树12m、高20m的一棵大树的最顶端发出友好的叫声,它立刻以4m/s的速度飞向大树的顶端,那么这只小鸟至少几秒才可能到达大树最顶端和伙伴在一起?15.如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.(1) 求梯子底端B外移距离BD的长度;(2) 猜想CE与BE的大小关系,并证明你的结论.16.如图,A 市气象站测得台风中心在A 市正东方向 300 km 的 B 处,以 10√7 km/h 的速度向北偏西 60∘ 的 BF 方向移动,距台风中心 200 km 范围内是受台风影响的区域.(1) A 市是否会受到台风的影响?写出你的结论并给予说明;(2) 如果A 市受这次台风影响,那么受台风影响的时间有多长?17.如图,ACB △和ECD 都是等腰直角三角形,,,CA CB CD CE ACB ==△的顶点A 在ECD 的斜边DE 上,连接BD .(1)求证:BD AE =. (2)若3cm,6cm AE AD ==,求AC 的长。
勾股定理练习题及答案

勾股定理练习题及答案勾股定理练习题及答案勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。
下面小编给大家带来勾股定理练习题及答案,欢迎大家阅读。
勾股定理练习题:1、在Rt△ABC中,∠B=90°,BC=15,AC=17,以AB为直径作半圆,则此半圆的面积为__________2、已知直角三角形两边的长为3和4,则此三角形的周长为__________.3、某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要 __________元.4、如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3m.同时梯子的顶端B 下降至B′,那么BB′().A.小于1m B.大于1m C.等于1m D.小于或等于1m5、将一根24cm的.筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是().A.h≤17cm B.h≥8cmC.15cm≤h≤16cm D.7cm≤h≤16cm6、如图,某公园内有一棵大树,为测量树高,小明C处用侧角仪测得树顶端A的仰角为30°,已知侧角仪高DC=1。
4m,BC=30米,请帮助小明计算出树高AB.(取1。
732,结果保留三个有效数字)◆典例分析如图1,一个梯子AB长2。
5m,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1。
5m,梯子滑动后停在DE的位置上,如图2,测得BD长为0。
5m,求梯子顶端A下落了多少米.解法指导:直角三角形中,已知一直角边和斜边是勾股定理的重要应用之一.勾股定理:a2+b2=c2的各种变式:a2=c2-b2,b2=c2-a2.应牢固掌握,灵活应用.分析:先利用勾股定理求出AC与CE的长,则梯子顶端A下落的距离为AE=AC-CF.解:在Rt△ABC中,AB2=AC2+BC2∴2.52=AC2+1。
勾股定理经典例题(含答案)

勾股定理经典例题类型一:勾股定理的直接用法 1、在Rt △ABC 中,∠C=90°(1)已知a=6, c=10,求b , (2)已知a=40,b=9,求c; (3)已知c=25,b=15,求a.思路点拨: 写解的过程中,一定要先写上在哪个直角三角形中,注意勾股定理的变形使用。
举一反三【变式】:如图∠B =∠ACD =90°, AD =13,CD =12, BC =3,则AB 的长是多少?类型二:勾股定理的构造应用 2、如图,已知:在中,,,. 求:BC 的长。
1、某市在旧城改造中,计划在市内一块如图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a 元,则购买这种草皮至少需要( ) A 、450a 元 B 、225a 元C 、150a 元D 、300a 元举一反三【变式1】如图,已知:,,于P 。
求证:.150°20m30m【变式2】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2.求:四边形ABCD的面积。
类型三:勾股定理的实际应用(一)用勾股定理求两点之间的距离问题3、如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了到达B 点,然后再沿北偏西30°方向走了500m到达目的地C点.(1)求A、C两点之间的距离。
(2)确定目的地C在营地A的什么方向。
举一反三【变式】一辆装满货物的卡车,其外形高2。
5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?(二)用勾股定理求最短问题4、如图,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程.类型四:利用勾股定理作长为的线段5、作长为、、的线段.作法:如图所示举一反三【变式】在数轴上表示的点。
解析:可以把看作是直角三角形的斜边,,为了有利于画图让其他两边的长为整数,而10又是9和1这两个完全平方数的和,得另外两边分别是3和1.作法:如图所示在数轴上找到A点,使OA=3,作AC⊥OA且截取AC=1,以OC为半径,以O为圆心做弧,弧与数轴的交点B即为.类型五:逆命题与勾股定理逆定理6、写出下列原命题的逆命题并判断是否正确1.原命题:猫有四只脚.(正确)2.原命题:对顶角相等(正确)3.原命题:线段垂直平分线上的点,到这条线段两端距离相等.(正确)4.原命题:角平分线上的点,到这个角的两边距离相等.(正确)7、如果ΔABC的三边分别为a、b、c,且满足a2+b2+c2+50=6a+8b+10c,判断ΔABC的形状。
完整版)勾股定理培优专项练习

完整版)勾股定理培优专项练习勾股定理练(根据对称求最小值)基本模型:已知点A、B为直线m同侧的两个点,请在直线m上找一点M,使得AM+BM有最小值。
1、已知边长为4的正三角形ABC上一点E,AE=1,AD⊥BC于D,请在AD上找一点N,使得EN+BN有最小值,并求出最小值。
解:由于AE=1,所以DE=√3.连接BE,设∠EBN=x,则∠EBD=∠ABE-x=60°-x。
由正弦定理得:EN/ sinx = BN/sin(60°-x)。
=。
EN/BN = sinx/sin(60°-x)由于sinx/sin(60°-x)在[0,1]内单调递增,所以EN/BN最小值对应的x值也是最小值。
又由于XXX,所以问题转化为:在直线AD上找一点N,使得MN+EB最小。
连接AC,设交点为F,则∠ABF=∠FBD=30°,BF=AB/2=2.由于AF=AD-DF=√3-DF,所以MN+EB=BF+MN+EF=BF+FN。
由于FN=AF-AN=AF-AE=√3-1,所以MN+EB=2+MN+√3-1=MN+3+√3.因此,EN+BN的最小值为3+√3,此时x=30°。
2、已知边长为4的正方形ABCD上一点E,AE=1,请在对角线AC上找一点N,使得EN+BN有最小值,并求出最小值。
解:连接BE,设∠EBN=x,则∠EBD=∠ABE-x=45°-x。
由正弦定理得:EN/sinx = BN/sin(45°-x)。
=。
EN/BN = sinx/sin(45°-x)由于sinx/sin(45°-x)在[0,1]内单调递增,所以EN/BN最小值对应的x值也是最小值。
又由于XXX,所以问题转化为:在对角线AC上找一点N,使得MN+EB最小。
连接BD,设交点为F,则∠ABF=∠FBD=45°,BF=AB/√2=2√2.由于AF=AD-DF=4-DF,所以MN+EB=BF+MN+EF=BF+FN。
勾股定理练习题(含答案)
勾股定理练习题一、基础达标:1. 下列说法准确的是( )A.若 a 、b 、c 是△ABC 的三边,则a 2+b 2=c 2;B.若 a 、b 、c 是Rt△ABC 的三边,则a 2+b 2=c 2;C.若 a 、b 、c 是Rt△ABC 的三边, 90=∠A ,则a 2+b 2=c 2;D.若 a 、b 、c 是Rt△ABC 的三边, 90=∠C ,则a 2+b 2=c 2. 2. Rt △ABC 的三条边长分别是a 、b 、c ,则下列各式成立的是( )A .c b a =+ B. c b a >+ C. c b a <+ D. 222c b a =+ 3. 如果Rt △的两直角边长分别为k 2-1,2k (k >1),那么它的斜边长是( )A 、2kB 、k+1C 、k 2-1D 、k 2+1 4. 已知a ,b ,c 为△ABC 三边,且满足(a 2-b 2)(a 2+b 2-c 2)=0,则它的形状为( )A.直角三角形B.等腰三角形C.等腰直角三角形D.等腰三角形或直角三角形 5. 直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )A .121B .120C .90D .不能确定 6. △ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为( ) A .42 B .32 C .42 或 32 D .37 或 33 7.※直角三角形的面积为S ,斜边上的中线长为d ,则这个三角形周长为( )(A 2d (B d(C )2d (D )d8、在平面直角坐标系中,已知点P 的坐标是(3,4),则OP 的长为( )A :3B :4C :5D :79.若△ABC 中,AB=25cm ,AC=26cm 高AD=24,则BC 的长为( )A .17 B.3 C.17或3 D.以上都不对10.已知a 、b 、c 是三角形的三边长,如果满足2(6)100a c --=则三角形的形状是( )A :底与边不相等的等腰三角形B :等边三角形C :钝角三角形D :直角三角形 11.斜边的边长为cm 17,一条直角边长为cm 8的直角三角形的面积是 .12. 等腰三角形的腰长为13,底边长为10,则顶角的平分线为__. 13. 一个直角三角形的三边长的平方和为200,则斜边长为 14.一个三角形三边之比是6:8:10,则按角分类它是 三角形. 15. 一个三角形的三边之比为5∶12∶13,它的周长为60,则它的面积是___.16. 在Rt △ABC 中,斜边AB=4,则AB 2+BC 2+AC 2=_____.17.若三角形的三个内角的比是3:2:1,最短边长为cm 1,最长边长为cm 2,则这个三角形三个角度数分别是 ,另外一边的平方是 .18.如图,已知ABC ∆中,︒=∠90C ,15=BA ,12=AC ,以直角边BC 为直径作半圆,则这个半圆的面积是 .19. 一长方形的一边长为cm 3,面积为212cm ,那么它的一条对角线长是 .ACB二、综合发展:1.如图,一个高4m 、宽3m 的大门,需要在对角线的顶点间加固一个木条,求木条的长.2、有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC 沿∠CAB 的角平分线AD 折叠,使它落在斜边AB 上,且与AE 重合,你能求出CD 的长吗?3.一个三角形三条边的长分别为cm 15,cm 20,cm 25,这个三角形最长边上的高是多少?4.如图,要修建一个育苗棚,棚高h=3m ,棚宽a=4m ,棚的长为12m ,现要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?AECDB5.如图,有一只小鸟在一棵高13m 的大树树梢上捉虫子,它的伙伴在离该树12m ,高8m 的一棵小树树梢上发出友好的叫声,它立刻以2m/s 的速度飞向小树树梢,它最短要飞多远?这只小鸟至少几秒才可能到达小树和伙伴在一起?15.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30m 处,过了2s 后,测得小汽车与车速检测仪间距离为50m ,这辆小汽车超速了吗?A小汽车小汽车BC观测点答案:一、基础达标1. 解析:利用勾股定理准确书写三角形三边关系的关键是看清谁是直角.答案: D.2. 解析:本题考察三角形的三边关系和勾股定理.答案:B.3. 解析:设另一条直角边为x ,则斜边为(x+1)利用勾股定理可得方程,可以求出x .然后再求它的周长. 答案:C .4.解析:解决本题关键是要画出图形来,作图时应注意高AD 是在三角形的内部还是在三角形的外部,有两种情况,分别求解. 答案:C.5. 解析: 勾股定理得到:22215817=-,另一条直角边是15,所求直角三角形面积为21158602cm ⨯⨯=.答案: 260cm .6. 解析:本题目主要是强调直角三角形中直角对的边是最长边,反过来也是成立.答案:222c b a =+,c ,直角,斜,直角.7. 解析:本题由边长之比是6:8:10 可知满足勾股定理,即是直角三角形.答案:直角. 8. 解析:由三角形的内角和定理知三个角的度数,断定是直角三角形.答案:︒30、︒60、︒90,3. 9. 解析:由勾股定理知道:22222291215=-=-=AC AB BC ,所以以直角边9=BC 为直径的半圆面积为10.125π.答案:10.125π.10. 解析:长方形面积长×宽,即12长×3,长4=,所以一条对角线长为5. 答案:cm 5. 二、综合发展11. 解析:木条长的平方=门高长的平方+门宽长的平方.答案:5m .12解析:因为222252015=+,所以这三角形是直角三角形,设最长边(斜边)上的高为xcm ,由直角三角形面积关系,可得1115202522x ⨯⨯=⨯⋅,∴12=x .答案:12cm13.解析:透阳光最大面积是塑料薄膜的面积,需要求出它的另一边的长是多少,可以借助勾股定理求出.答案:在直角三角形中,由勾股定理可得:直角三角形的斜边长为5m,所以矩形塑料薄膜的面积是:5×20=100(m 2) .14.解析:本题的关键是构造直角三角形,利用勾股定理求斜边的值是13m ,也就是两树树梢之间的距离是13m ,两再利用时间关系式求解. 答案:6.5s . 15.解析:本题和14题相似,可以求出BC 的值,再利用速度等于路程除以时间后比较.BC=40米,时间是2s ,可得速度是20m/s=72km/h >70km/h . 答案:这辆小汽车超速了.。
勾股定理练习题及答案
勾股定理练习题及答案勾股定理是数学中的一条基本定理,被广泛应用于几何学和物理学等领域。
它的形式简单,但是应用广泛,可以解决很多实际问题。
在这篇文章中,我们将通过一些练习题来巩固和应用勾股定理。
练习题一:已知直角三角形的斜边长为10,一条直角边长为6,请计算另一条直角边的长度。
解答一:根据勾股定理,直角边的平方和等于斜边的平方。
设另一条直角边的长度为x,则有:x^2 + 6^2 = 10^2化简得:x^2 = 100 - 36x^2 = 64x = 8练习题二:已知一个直角三角形的两条直角边分别为3和4,请计算斜边的长度。
解答二:同样地,根据勾股定理,斜边的平方等于直角边的平方和。
设斜边的长度为y,则有:y^2 = 3^2 + 4^2y^2 = 9 + 16y = 5练习题三:已知一个直角三角形的斜边长为13,一条直角边长为5,请计算另一条直角边的长度。
解答三:同样地,根据勾股定理,直角边的平方和等于斜边的平方。
设另一条直角边的长度为z,则有:z^2 + 5^2 = 13^2z^2 + 25 = 169z^2 = 144z = 12通过以上的练习题,我们可以看到勾股定理在解决直角三角形问题时的应用。
它通过简单的数学关系,将三角形的边长联系起来,帮助我们求解未知边长。
这在实际生活中也有广泛的应用,比如测量建筑物的高度、计算斜坡的倾斜度等等。
除了直角三角形,勾股定理还可以应用于其他几何图形。
例如,我们可以利用勾股定理计算矩形的对角线长度。
设矩形的长为a,宽为b,则对角线的长度d 可以通过以下公式计算:d^2 = a^2 + b^2此外,勾股定理还可以用于解决一些物理问题。
例如,当我们知道一个物体在斜面上的高度差和斜面的倾斜角度时,可以利用勾股定理计算物体在斜面上的总之,勾股定理是一条简单而重要的数学定理,它的应用范围广泛,可以解决很多实际问题。
通过练习题的实践,我们可以更好地理解和应用这一定理。
希望本文对你有所帮助!。
勾股定理练习题及答案(共6套)
勾股定理课时练(1)的值是()1.在直角三角形ABC中,斜边AB=1,则AB2+眈2€AC2A.2B.4C.6D.82•有一个形状为直角梯形的零件ABCD,AD〃BC,斜腰DC的长为10cm,Z D=120°,则该零件另一腰AB的长是cm(结果不取近似值).3.__________________________________________________ 直角三角形两直角边长分别为5和12,则它斜边上的高为•4•一根旗杆于离地面12m处断裂,犹如装有铰链那样倒向地面,旗杆顶落于离旗杆地步16m,旗杆在断裂之前高多少m?5•如图,如下图,今年的冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在离树杆底部4米处,那么这棵树折断之前的高度是米.第5题图6.飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,求飞机每小时飞行多少千米?7.如图所示,无盖玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的容器的上口外侧距开口1cm的F处有一苍蝇,试求急于扑货苍蝇充饥的蜘蛛,所走的最短路线的长度.第7题图8.一个零件的形状如图所示,已知AC=3cm,AB=4cm,BD=12cm。
求CD的长.第8题图9.如图,在四边形ABCD中,ZA=60°,ZB=ZD=90°,BC=2,CD=3,求AB的长.n第9题图10.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家•他要完成这件事情所走的最短路程是多少?11如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯平方米18元请你帮助计算一下,铺完这个楼道至少需要多少元钱?5m12.甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?、选择题1•下列各组数据中,不能作为直角三角形三边长的是(2•满足下列条件的三角形中,不是直角三角形的是()C.三边之比为訂:2:驀D.三个内角比为1:2:33•已知三角形两边长为2和6,要使这个三角形为直角三角形,则第三边的长为()A 迈B.^10C.4-込或2颅D.以上都不对4. 五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是()CD25,则三角形的最大内角的度数是.其面积为. 7•已知三角形ABC 的三边长为a ,b ,c 满足.「,c=8,则此三角形为三角形.a +b 二10,ab=188. 在三角形ABC 中,AB=12cm ,AC=5cm ,BC=13cm ,则BC 边上的高为AD=cm . 三、解答题9. 如图,已知四边形ABCD 中,Z B =90°,AB =3,BC =4,CD =12,AD =13,求四边形ABCD 的面积.第9题图勾股定理的逆定理(2)A.9,12,15B.C.0.2,0.3,0.4D.40,41,9A.三个内角比为1:2:1B.三边之比为1:2:A B二、填空题5.△ABC 的三边分别是7、24、6•三边为9、12、15的三角(A)(B)(C)25 (D)110.如图,E、F分别是正方形ABCD中BC和CD边上的点,且AB=4,CE=4BC,F为CD的中点,连接AF、AE,问A AEF是什么三角形?请说明理由.11.如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处上爬到树顶A处,利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子所经路程都是15m,求树高AB.12.如图,为修通铁路凿通隧道AC,量出ZA=40°ZB=50°,AB=5公里,BC=4公里,若每天凿隧道0.3公里,问几天才能把隧道AB凿通?勾股定理的逆定理(3)一、基础•巩固1•满足下列条件的三角形中,不是直角三角形的是()A.三内角之比为1:2:3B.三边长的平方之比为1:2:3C.三边长之比为3:4:5D.三内角之比为3:4:5二、综合•应用9.如图18—2—9所示,在平面直角坐标系中,点A、B的坐标分别为A(3,1),B(2,4),△OAB是直角三角形吗?借助于网格,证明你的结论12.已知:如图18—2—10,四边形ABCD,AD〃BC,AB=4,BC=6,CD=5,AD=3.求:四边形ABCD勾股定理的应用(4)2.求知中学有一块四边形的空地ABCD,如下图所示,学校计划在空地上种植草皮,经测量ZA=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200天,问学校需要投入多少资金买草皮?3..(12分)如图所示,折叠矩形的一边AD,使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,求EC的长。
勾股定理练习(含答案)
勾股定理练习一、单选题(共12题;共24分)1.如图,长为8cm 的橡皮筋放置在x 轴上,固定两端A和B,然后把中点C向上拉升3cm 至D点,则橡皮筋被拉长了()A. 2cmB. 3cmC. 4cmD. 5cm2.如图,在Rt△ABC中,∠C=90°,如果AB=5,BC=3,那么AC等于()A. B. 3 C. 4 D. 53.在下列的线段中,能组成直角三角形的是( )A. 1,2,3B. 2,3,4C. 3,4,5D. 4,5,64.如果梯子的底端离建筑物5 米,13 米长的梯子可以达到该建筑物的高度是()A. 12 米B. 13 米C. 14 米D. 15 米5.一直角三角形两边分别为3和5,则第三边为()A. 4B.C. 4或D. 26.在△ABC中,∠C=90°,若AC=3,BC=4,则AB=()A. B. 5 C. D. 77.如图,一个梯子AB长2.5 米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.9米,则梯子顶端A下落了()A. 0.9米B. 1.3米C. 1.5米D. 2米8.若直角三角形的三边长分别为2、4、x,则x的可能值有()A. 1个B. 2个C. 3个D. 4个9.如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距()A. 25海里B. 30海里C. 40海里D. 50海里10.一个圆桶底面直径为24cm,高32cm,则桶内所能容下的最长木棒为()A. 20cmB. 50cmC. 40cmD. 45cm11.如图所示:某商场有一段楼梯,高BC=6m,斜边AC是10米,如果在楼梯上铺上地毯,那么需要地毯的长度是()A. 8mB. 10mC. 14mD. 24m12.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B 恰好碰到地面,经测量AB=2米,则树高为()A. 米B. 米C. (米D. 3 米二、填空题(共8题;共8分)13.在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为________cm2.14.若直角三角形两直角边长分别为6和8,则它的斜边长为________.15.直角三角形两直角边长分别为,,则斜边长为________.16.如图,作一个长方形,以数轴的原点为中心,长方形对角线为半径,交数轴于点A,则点A表示的数是________.17.如图,小华将升旗的绳子拉到竖直旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,此时绳子末端距离地面2m,则绳子的总长度为________ m.18.已知一个直角三角形的两条直角边的差为2,两条直角边的平方和为8,则这个直角三角形的面积是________19.已知Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,则Rt△ABC的面积等于________ cm2.20.学校有一块长方形的花圃如右图所示,有少数的同学为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了________步(假设1米=2步),却踩伤了花草,所谓“花草无辜,踩之何忍”!三、作图题(共1题;共5分)21.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫格点,以格点为顶点,①在图1中画出边长分别为:3,2 ,的三角形(不写画法);②在图2中画出边长分别为,4,,4的平行四边形(不写画法).四、计算题(共1题;共5分)22.已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.23.有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行多什么米?24.如图,梯形ABCD是由三个直角三角形拼成的,各直角边的长度如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
边长、周长
例一:如图,有一只小鸟在一棵高13m 的大树的树顶上捉虫子,它的伙伴在离该树12m ,高8m 的一棵小树上发出友好的叫声,它立刻以2m/s 的速度飞向小树树顶,它最短要飞多远?
1.在△ABC 中,∠C=90°。
(1)若c=61,b=60,则a= ______
(2)若a:b=3:4,c=10,则a=____ ,b=______ 。
2.如图,一架长2.5m 的梯子AB ,斜靠在一竖直的墙AC 上,这时梯足B 到墙底端C 的距离为0.7m ,若梯子的顶端沿墙下滑0.4m 。
那么梯足将外移多少米? 练习
1. 一个直角三角形的三边长的平方和为200,则斜边长为
2.直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为_____
C A A
B
B
3.等腰三角形的腰长为13,底边长为10,则顶角的平分线为__. 分类讨论
已知两边求第三边时,若没有明确已知的是什么边,则必须分类讨论。
1.已知6、8、a 是一个三角形的三边长,若该三角形为直角三角形,那么a 是多少?
2.已知△ABC 中,AB=17,AC=10.BC 上的高为8.求
BC.
练习1.若△ABC 中,AB=25cm ,AC=26cm 高AD=24,则BC 的长为()
A
B
C
D
A
B
C
D
1.在△ABC中,∠C=90°。
(1)若c=25,b=24,则a= ______
(2)若a:b=5:12,c=26,则a=____ ,b=_____ 。
2.若一个三角形的三边长为m+1,8,m+3,当m=______时,此三角形是直角三角形,且其中m+3是斜边。
3.如图,在△ABC中,∠ACB=90°,BC=5cm,AC=12cm,CD⊥AB,D
4. △ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为
面积
例一:如图,A,B,C 分别是以a 、b 、c 为边长 的正方形面积A=81,C=225.求B=___
1.如图所示,已知四边形ABCD 中,AD=3cm ,AB=4cm ,DC=12cm ,BC=13cm ,且AB ⊥AD 。
求四边形ABCD 的面积。
2.如图,已知ABC ∆中,︒=∠90C ,15=BA ,12=AC ,以直角边BC 为直径作半圆,则这个半圆的面积是 .
例二:如图,分别以直角三角形ABC 三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1,S2,S3之间的关系并加以证明;
1:如图,分别以直角三角形ABC 三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,S1、S2、S3的半径分别为r1,r2,r3.
(1)AC=6,CB=8.求S1=____
(2)S1=23,S2=144.求S1=_____
练习:1.如图,A,B,C 分别是以a 、b 、c 为边长 的正方形面积A=225,B=400.求C=___
2.如图,分别以直角三角形ABC 三边为边向外 作三个正三角形,其面积分别用S1、S2、S3表示 (1)AC=6,AB=10.求S2=____
(2)S1、S2、S3的半径分别为r1,r2,r3. S1=100,S2=64.求S3=_____
3.如图,已知ABC ∆中,︒=∠90C ,15=BA ,
12=AC ,以直角边BC 为直径作半圆,
则这个半圆的面积是 .
4.在Rt △ABC 中,斜边AB=4,则AB 2+BC 2+AC 2=_____
拱桥问题与台风问题
1、如图,某隧道的截面是一个半径为3.6米的半圆形,一辆高2.4米,宽3米的卡车能通过该隧道吗? 练习
1.如图,某隧道的截面是一个半径为5米的半圆 形,一辆高3米,宽3米的卡车能通过该隧 道吗?
2.如图,某隧道的截面是一个直径是为13米的半圆形,一辆高12米,
宽6米的卡车能通过该隧道吗?
3.如图,某沿海开放城市A 接到台风警报,在该市正南方向100km 的B 处有一台风中心,沿BC 方向以20km/h 的速度向D 移动,已知城市A 到BC 的距离AD=60km ,那么台风中心经过多长时间从B 点移到D 点?如果在距台风中心30km 的圆形区域内都将有受到台风的破坏的危险,正在D 点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?
A
B
D
C
题型四:最短路径问题(空间问题转化为平面问题)
例一:有一个圆柱,它的高等于8厘米,底面半径等于2厘米,在圆柱下底面上的A 点有一只蚂蚁,它想从点A 爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少? 圆周率π按3来计算
例二:长方体的高为3cm,长为4cm ,宽为2cm.现有一小虫从顶点A 出发,沿长方体表面到达顶点E,小虫走的路程最短为____厘米.
A
B
C
D
E
F G
H
A
B
H
G
E
C
A B
G H
E F
E
H
F
G
D
A
练习
1.有一个圆柱,它的高等于8厘米,底面半径等于1厘米,在圆柱下底面上的A 点有一只蚂蚁,它想从点A 爬到点B ,B 在高的中点, 蚂蚁沿着圆柱侧面爬行的最短路程是多少? 圆周率π按3来计算
2.一个无盖的长方体纸盒的高为3cm,长为4cm ,宽为2cm.现有一小虫从顶点A 出发,沿长方体表面到达顶点E,小虫走的路程最短为____厘米.
3.如图,正方体是由所有边长为1cm 的小正方形组成.蚂蚁从底而A 出沿着表面积而爬到右侧点B 处,至少要爬行
__________cm
4.如图圆柱形容器高1.2m ,底面周长1m ,在容器内壁离底部0.3m 的B 处有一只蚊子,此时一壁虎正好在容器外壁且离上沿0.3m 与蚊子相对的A 处,则壁虎捕捉蚊子的最短距离是多少?
A
B
5.长方体的高为3cm,底面是边长为2cm 的正方形.现有一小虫从顶点A 出发,沿长方体侧面到达顶点C,小虫走的路程最短为____厘米. .
C
A
A
C
B
B
A
难点
例一:如图,圆柱底面半径为2cm,高为9πcm,点A 、B 分别是圆柱两底面圆周上的点,且A 、B 在同一母线上,用一棉线从A 顺着圆柱侧面绕3圈到B,求棉线最短为
分析:
可以想象把圆柱形沿着AB 母线打开,成为长方形.红色的实线就是棉线的轨迹 AC 用勾股定理求出 AC 的平方=(4π)2+(3π)2=(5π)2 最短的距离即3*AC=3*5π=15π
练习
我国古代有这样一道数学问题,枯木一根直立在地上,高2丈,周3尺,有葛藤条自根缠绕而上,五周而达其顶,问葛藤之长几何?题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺底面周长为3尺,有葛藤自点A 处缠绕而上绕五周后其末端恰好到达点B 处,求问题中葛藤的最短长度是多少尺?
E
B
B
判定直角三角形
1、已知a、b、c是三角形的三边长,如果满足2
a b c
-+-+-=
(6)8100
则三角形的形状是()
A:底与边不相等的等腰三角形 B:等边三角形C:钝角三角形 D:直角三角形2、若(13-c)2+|a-12|+(b-5)2=0,则以a、b、c为三边的三角形是____________三角形
3、已知a,b,c为△ABC三边,且满足(a2-b2)(a2+b2-c2)=0,则它的形状为()
A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
练习
1.若(13-c)2+a2+(b-5)2+144=24a,则以a、b、c为三边的三角形是____________三角形
2.若c2+a2+b2+100=6a+8b+10c,则以a、b、c为三边的三角形是
____________三角形
3.若c2+a2+b2+200=12a+16b+20c,则以a、b、c为三边的三角形是____________三角形。
