数学实验(matlab)(矩阵创建与二元函数图形)教育技术作业
matlab实验指导2019-11-12

实验1 熟悉软件环境和基本的操作一、实验目的熟悉MATLAB运行环境和了解基本操作。
二、实验内容MATLAB的启动、操作界面组成1.熟悉MATLAB图形界面打开MATLAB,单击命令窗口菜单栏中的各个下拉菜单按钮,试使用各个按钮引出的选项;把光标移动到工具栏中各个图标上(不要按下),查看它们与菜单选项的对应情况。
2.熟悉MATLAB的基本命令。
在命令窗口中分别键入以下内容,以建立若干变量:A=[1 2;3 4;5 6]B=[7,8,9;10,11,12]C=[5 6 7;1 8 3];D=B+C问题1:如何输入一个矩阵变量的行元素和列元素?问题2:观察每行命令后是否加“;”,对显示执行结果有什么区别?键入以下命令或执行操作,查看效果,并体会命令功能:(1)工作空间管理。
whowhosclear A(2)路径编辑。
试用菜单File/Set Path将D盘根目录及其下的所有子目录和文件夹包含进来,设为搜索路径。
问题3:当前路径是什么?问题4:搜索路径是什么意思?(3)联机帮助help pausehelpwin(4)窗口清理。
先画出正弦函数在0-2π之间的图形,再用以下各种窗口清理命令,看每项命令都清除了什么。
figureplot(sin(0:0.1:6.28))claclfclose注意:figure为打开一幅图形图像窗口close为关闭当前图形图像窗口,而close all为关闭所有已打开的图形图像窗口。
(5)MATLAB基本矩阵操作演示playshow intro(6)MATLAB图形绘制演示playshow buckydem(7)MATLAB数学功能演示(快速傅氏变换)playshow fftdemo(8)MATLAB三维造型演示(茶壶演)playshow teapotdemo3.打开MATLAB命令窗口,键入demos,观看演示程序。
三、思考题1.将pi分别用15位数字格式、分数格式、十六进制格式、5位数字的科学计数法显示。
matlab矩阵实验报告

matlab矩阵实验报告《MATLAB矩阵实验报告》摘要:本实验报告利用MATLAB软件进行了矩阵实验,通过对矩阵的运算、转置、逆矩阵、特征值等操作进行了分析和讨论。
实验结果表明,MATLAB在矩阵运算方面具有高效、准确的特点,能够满足工程和科学计算的需求。
引言:矩阵是线性代数中的重要概念,广泛应用于工程、物理、经济等领域。
MATLAB是一种强大的数学软件,能够对矩阵进行各种运算和分析。
本实验旨在利用MATLAB软件对矩阵进行实验,探讨其在矩阵运算中的应用和优势。
实验方法:1. 创建矩阵:利用MATLAB软件创建不同大小的矩阵,包括方阵和非方阵。
2. 矩阵运算:进行矩阵的加法、减法、乘法等运算,比较不同大小矩阵的计算效率和结果准确性。
3. 矩阵转置:对矩阵进行转置操作,观察转置后矩阵的性质和应用。
4. 逆矩阵:求解矩阵的逆矩阵,并分析逆矩阵在实际问题中的应用。
5. 特征值和特征向量:利用MATLAB软件求解矩阵的特征值和特征向量,分析其在物理、工程等领域的应用。
实验结果与讨论:通过实验发现,MATLAB软件在矩阵运算中具有高效、准确的特点。
对于大规模矩阵的运算,MATLAB能够快速进行计算并给出准确的结果。
在矩阵转置和逆矩阵求解方面,MATLAB也能够满足工程和科学计算的需求。
此外,通过求解矩阵的特征值和特征向量,可以得到矩阵的重要性质,为实际问题的分析和求解提供了有力支持。
结论:本实验利用MATLAB软件进行了矩阵实验,通过对矩阵的运算、转置、逆矩阵、特征值等操作进行了分析和讨论。
实验结果表明,MATLAB在矩阵运算方面具有高效、准确的特点,能够满足工程和科学计算的需求。
希望本实验能够对矩阵运算和MATLAB软件的应用有所启发,为相关领域的研究和应用提供参考。
实验四 MATLAB 二维绘图的基本操作

实验四 MATLAB 二维绘图的基本操作一、实验目的通过图形可以从一堆杂乱的数据中观察数据间的内在关系,感受由图形所传递的内在本质。
本实验主要练习并掌握二维曲线绘图的基本操作。
Time(seconds)M a k e s p a n二、实验内容在了解了 MATLAB 的矩阵和向量概念与输入方法之后,MA TLAB 的二维绘图就再简单不过了。
假设有两个同长度的向量 x 和 y, 则用 plot(x,y) 就可以自动绘制画出二维图来。
如果打开过图形窗口,则在最近打开的图形窗口上绘制此图,如果未打开窗口,则开一个新的窗口绘图。
〖例〗正弦曲线绘制,在命令窗口依次输入如下指令:>> t=0:.1:2*pi; %生成横坐标向量,使其为 0,0.1,0.2,...,6.2>> y=sin(t); % 计算正弦向量>> plot(t,y) %绘制图形这样立即可以得出如下图所示的二维图:10.80.60.40.2-0.2-0.4-0.6-0.8-1plot 函数还可以同时绘制出多条曲线,其调用格式和前面不完全一致,但也好理解。
在命令窗口接着输入:>> y1=cos(t);>>plot(t,[y; y1]), 即输出为两个行向量组成的矩阵。
所得图形如下:10.80.60.40.2-0.2-0.4-0.6-0.8-1★plot 的基本调用格式:plot(x1,y1,选项1, x2,y2, 选项2, x3,y3, 选项3, ...),其中所有的选项如表4.1 所示。
一些选项可以连用,如'-r' 表示红色实线。
练习:>> plot(x,y,'--')>> plot(x,y,'b')>> plot(x,y,'r')>> plot(x,y,'o')由MA TLAB 绘制的二维图形可以由下面的一些命令简单地修饰。
实验二MATLAB绘制图形

grid on %在所画出的图形坐标中加入栅格
绘制图形如下
50
10
1
0.8
40
10
0.6
0.4
30
10
0.2
0
1020
-0.2
-0.4
1010
-0.6
-0.8
0
10
-1
-2
0
2
-2
0
2
10
10
10
10
10
10
如果在图中不加栅格
程序如下:
clear x=logspace(-1,2);%在10^(-1)到10^2之间产生50个 对数等分的行向量 subplot(121); loglog(x,10*exp(x),'-p') subplot(122); semilogx(x,cos(10.^x))
(2)plot(x,y): 基本格式,x和y可为向量或矩阵. 1. 如果x,y是同维向量,以x元素为横坐标,以y元素 为纵坐标绘图. 2. 如果x是向量,y是有一维与x元素数量相等的矩阵, 则以x为共同横坐标, y元素为纵坐标绘图,曲线数目 为y的另一维数. 3. 如果x,y是同维矩阵,则按列以x,y对应列元素为 横、纵坐标绘图,曲线数目等于矩阵列数.
y=2*exp(-0.5*x).*cos(4*pi*x);
2
plot(x,y)
1.5
1
0.5
0
-0.5
-1
-1.5
-2
0
1
2
3
4
5
6
7
例4 绘制曲线
t=(0:0.1:2*pi);
x=t.*sin(3*t);
y=t.*sin(t).*sin(t);
实训三 MATLAB 矩阵建立与运算

物理与工程技术学院实验报告班级: 17物理分组: 姓名:陈俊聪学号: 04同组人:日期:教师评分:实验名称:实训三矩阵建立与运算一、目的1.了解MATLAB基本运算对象,即矩阵:2.通过输入矩阵中每个元素的值来建立一个矩阵;3.矢量法创建矩阵,学会使用冒号和数字产生矢量:4.函数法创建矩阵,利用函数可以快速产生- -些特殊有用的矩阵;5.掌握矩阵的基本运算:矩阵与标量的运算,矩阵与矩阵的运算,提取子块,矩阵的展开,矩阵的线性变换。
二、仪器电脑显示器、电脑主机、键盘、鼠标、MATLAB 软件三、内容1.通过输入矩阵中每个元素的值来创立-一个矩阵,只需以左方括号,以逗号或空格为间隔输入元素值,行与行之间用分号或单击Enter键隔开,最后以右方括号结尾即可。
当矩阵中元素个数比较少是,这种方法非常适用。
另外,用单引号界定的字符或字符串可以创字符例【1-6】创建3X3数值矩阵A, B和字符矩阵C。
例【1-7】建立一个10以内的奇数矩阵。
例【1-8】建立空矩阵A、单位矩阵B、常数矩阵C、均匀分布随机矩阵D、正正态分布的随机矩阵E、零矩阵F。
例【1-9】已知矩阵A=[1 2 3;4 5 6],标量b=3,计算A+b、A*b、A/b和A.^b。
例【1-10】已知矩阵A=[1 2;3 4],矩阵B=[5 6;7 8],求A*B、A.*B、A\B、A/B和A./B的运算结果。
例【1-11】输入一个4×3的矩阵,选出前3行构成一个矩阵;选出前两列构成一个矩阵。
例【1-12】把矩阵A=[1 3 5;7 9 11]和矩阵B=[2 4 6]合并成一个矩阵,再转置后展开。
例【1-13】建立-一个3×3的魔方矩阵,提取其对角元素和下三角矩阵,并上下翻转。
例【1-14】例[1-14] 将矩阵转化为稀疏矩阵B,并察看;再将稀疏矩阵B转化为完全矩阵C。
例【1-15】已知矩阵A=[1,3,5,7,9],找出大于4的元素的位置。
数学建模实验报告(一)MATLAB中矩阵的基本操作

1.5270
j =
2 3 2 5 1 4
>> min(a,[],1)
ans =
Columns 1 through 5
-2.3299 -0.1303 -1.3617 -1.1176 -0.3031
Column 6
0.0230
>> min(a,[],2)
ans =
-0.4762
-0.0679
-2.3299 -0.1303 0.4550 -1.1176 -0.2176
-1.4491 0.1837 -0.8487 1.2607 -0.3031
Column 6
0.0230
0.0513
0.8261
1.5270
0.4669
>> size(a)
ans =
5 6
>> [i,j]=find(a==max(max(a)))
-1.0000 2.5000 1.0000
3.5000 5.5000 2.5000
>> X=D
X =
4.0000 1.5000 -1.0000
-1.0000 2.5000 1.0000
3.5000 5.5000 2.5000
5、利用randn(5,6)命令生成一个随机矩阵T,求T的矩阵大小,每一行、每一列的最大值和最小值,整个矩阵的最大值与最小值;然后将整个矩阵的最大值所在位置的元素换为100,将最小值所在位置的元素取为-100。
(2):>> a=[2 5 8;7 1 9]
a =
2 5 8
7 1 9
>> b=[4 2 1 3;0 7 6 2;-3 5 9 -1]
实验二用matlab绘制一元函数与二元函数的图象
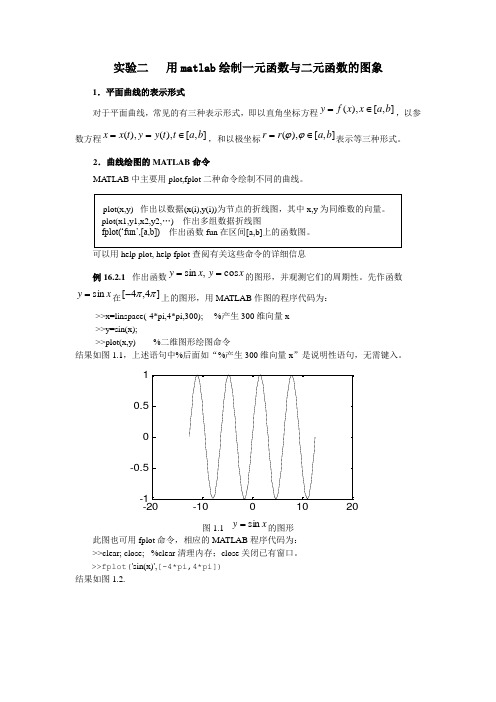
实验二 用matlab 绘制一元函数与二元函数的图象1.平面曲线的表示形式对于平面曲线,常见的有三种表示形式,即以直角坐标方程],[),(b a x x f y ∈=,以参数方程],[),(),(b a t t y y t x x ∈==,和以极坐标],[),(b a r r ∈=ϕϕ表示等三种形式。
2.曲线绘图的MATLAB 命令MATLAB 中主要用plot,fplot 二种命令绘制不同的曲线。
可以用help plot, help fplot 查阅有关这些命令的详细信息例16.2.1 作出函数x y x y cos ,sin ==的图形,并观测它们的周期性。
先作函数x y sin =在]4,4[ππ-上的图形,用MA TLAB 作图的程序代码为:>>x=linspace(-4*pi,4*pi,300); %产生300维向量x >>y=sin(x);>>plot(x,y) %二维图形绘图命令结果如图1.1,上述语句中%后面如“%产生300维向量x ”是说明性语句,无需键入。
图1.1 的图形此图也可用fplot 命令,相应的MATLAB 程序代码为: >>clear; close; %clear 清理内存;close 关闭已有窗口。
>>fplot('sin(x)',[-4*pi,4*pi]) 结果如图1.2.图1.2xy sin=的图形如果在同一坐标系下作出两条曲线xy sin=和xy cos=在]2,2[ππ-上的图形,相应的MA TLAB程序代码为:>>x=-2*pi:2*pi/30:2*pi; %产生向量x>>y1=sin(x); y2=cos(x);>>plot(x,y1,x,y2,’:’)%’:’表示绘出的图形是点线结果如图1.3其中实线是xy sin=的图形,点线是xy cos=的图形。
matlab--函数图形绘制实验报告1

实验报告课程名称: 数学实验学院名称: 数学与统计学院班级:姓名:学号:2012-2013 学年第学期数学与统计学院制(二)参数方程作图例2: 画出星形线{ 及旋轮线{ 的图形解: 输入以下命令:%星形线作图t=linspace(0,2*pi,5000);x=2*(cos(t)).^3;y=2*(sin(t)).^3;plot(x,y),grid;结果:%旋轮线作图t=linspace(0,4*pi,5000); x=2*(t-sin(t));y=2*(1-cos(t));plot(x,y),axis equal; axis(0,8*pi,0,5);grid;结果:(三)极坐标方程图形例3:画出四叶玫瑰线的图形。
知其极坐标方程: ρ=acos(2 )。
解: 取a=5做图。
在命令窗口输入下命令theta=linspace(0,2*pi);r=2*cos(2*theta);polar(theta,r)结果:(四)空间曲面(线)的绘制例4: 绘制双曲抛物面z= 。
解:将其化为参数方程:{ , 编写m文件运行以下命令r=linspace(-4,4,30);s=r;[u,v]=meshgrid(r,s);x=u;y=v;z=(u.^2-v.^2)./4;surf(x,y,z);bix on;结果:(五)空间曲线在坐标平面上的投影曲面和投影柱面例5: 画出螺旋线{ , 在xOz面上的正投影曲线的图形。
解:化为参数方程{ , 运行下列程序t=linspace(-2*pi,2*pi);x=10*cos(t);z=2*t;h=plot(x,z);grid;xlabel('x');ylabel('z');set(h,'linewidth',2);结果:(一)实验分析:(二)在本次实验中我们初步了解了matlab。
(三)学会了一些简单绘图。
(四)在编制中我们要很明确“点乘的重要性”。
