习题课2:压强分布图,压力体,平面板,曲面版总压力计算
流体力学课后习题答案第二章

第二章 流体静力学2-1 密闭容器测压管液面高于容器内液面h=1.8m,液体密度为850kg/m3, 求液面压强。
解:08509.8 1.814994Pa p gh ρ==⨯⨯=2-2 密闭水箱,压力表测得压强为4900Pa,压力表中心比A 点高0.4米,A 点在液面下1.5m ,液面压强。
解:0()490010009.8(0.4 1.5) 49009800 1.15880PaM B A p p g h h ρ=+-=+⨯⨯-=-⨯=-2-3 水箱形状如图,底部有4个支座。
试求底面上的总压力和四个支座的支座反力,并讨论总压力和支座反力不相等的原因。
解:底面上总压力(内力,与容器内的反作用力平衡)()10009.81333352.8KN P ghA ρ==⨯⨯+⨯⨯=支座反力支座反力(合外力)3312()10009.8(31)274.4KN G g V V ρ=+=⨯⨯+=2-4盛满水的容器顶口装有活塞A ,直径d=0.4m ,容器底直径D=1.0m ,高h=1.8m 。
如活塞上加力为2520N(包括活塞自重)。
求容器底的压强和总压力。
解:压强2252010009.8 1.837.7kPa (0.4)/4G p gh A ρπ=+=+⨯⨯= 总压力 237.71/429.6KN P p A π=⋅=⨯⋅=2-5多管水银测压计用来测水箱中的表面压强。
图中高程单位为m ,试求水面的绝对压强。
解:对1-1等压面02(3.0 1.4)(2.5 1.4)p g p g ρρ+-=+-汞对3-3等压面 2(2.5 1.2)(2.3 1.2)a p g p g ρρ+-=+-汞将两式相加后整理0(2.3 1.2)(2.5 1.4)(2.5 1.2)(3.0 1.4)264.8kPap g g g g ρρρρ=-+-----=汞汞绝对压强 0.0264.8+98=362.8kPa abs a p p p =+=2-6水管A 、B 两点高差h 1=0.2m ,U 形管压差计中水银液面高差h 2=0.2m 。
压强的计算 PPT

小结:
压强公式: p F
S
液体压强公式: p gh
解题口决 公式概念要劳记, 题目要求要分清。 书写格式按要求, 单位统一并带好。
谢谢大家!
结束
压强的计算 PPT
压强公式: p F
S
液体压强公式: pgh
一、求规则固体对水平面的压强
例、 有一密度为ρ固,高为h固的圆柱体放
在水平桌面上,如图所示,求圆柱体对 桌面的压强P是多少?(ρ固、h固、g均为 已知)
解:由F=G=mg=ρ固V g=ρ固h固Sg p=F/s=ρ固h固Sg/s=ρ固h固g
一、求不规则容器中液体对容器底的压力 和容器对水平面的压强.
例、如图所示,放在水平桌面上的容器重 为1N ,内装有5N的水,水面高为8cm, 容器高为10cm,容器底面积为50cm2。求:
(1)水对容器底的压力?
(2)容器对桌面的压强?
解:(1)水对容器底的压强为:
P =ρgh=1.0×103kg/m3×10N/kg×8×10-2m = 8×102Pa
(2) F = G1+G= 0.5kg×10N/kg+1kg×10N/kg =15N S = 100cm2 = 1×10-2m2 由压强公式P = F/S得 P = 15N/1×10-2m2= 1500Pa
点拨:本题习惯方法是先由水的质量和密度求出水的体积,再根 据水的体积和容器的底面积求容器中水的深度,最后运用液体压 强公式P =ρgh求出水对容器底的压强。由于本题中的容器是规 则的,且容器平放置,因此可以利用压强定义式P = F/S直接求 出水对容器底部的压强(同学们,想一想(2)问是否也能用上 述的方法算出呢?)
静水压强的特性

§2-1 静水压强及其特性 §2-2重力作用下静水压强的分布规律 §2-3压强的计算基准和量度单位 §2-4测量压强的仪器 §2-5静水压强分布图 §2-6 作用在平面上的静水总压力 §2-7 作用在曲面上的静水总压力 §2-8液体平衡微分方程 §2-9重力和惯性力同时作用下液体的相对平衡
A0
P A
图2-1
二、静水压强的特性
1.静水压强的方垂直指向受压面或沿受压面的内法线方 向
这一特性可由反证法给予证明,如下图所示。
p
作用力
F
α
切向应力
2.静止液体中作用于同一点各个方向的静水压强都 相等。 证明如下:在静止流体中任取一微元四面体,对其进行 受力分析.
作用在ACD面上 的流体静压强 px
p p0 gh 98 1 9.81 107.8kN / m 解:
2
p0=pa
h
p p pa 107.8 98 9.8kN / m2
例2:如图已知, p0=50kN/m2,h=1m, 求:该点的绝对压强及相对压强 解:p p0 gh 50 1 9.8 1 59.8kN / m2
Xdx 0
p X p Y p Z pn
上式说明,在静止液体中,任一点静水压强的大小与作用 面的方位无关,但液体中不同点上的静水压强可以不等, 因此,静水压强是空间坐标的标量函数,即:
p p p dp dx dy dz x y z (2-2)
p p( X , Y , Z )
表 压强的单位及其换算表
帕 (Pa) 1 9.8 × 10 10.13 × 10 10.00 × 10 0.686 × 10
第2章水静力学

第二章 水静力学
例题图示
第二章 水静力学
二、静水压强分布图
根据静水力学基本方程及静水压 强的两个特性,可用带箭头的直线表 示压强的方向,用直线的长度表示压 强的大小,将作用面上的静水压强分 布规律形象而直观地画出来。
w
FP pc w
w w
依力矩定理, P yD y dP y gy sin dw g sin y 2 dw
2 2 I I y y dw 其中 为平面对Ob轴的面积惯性矩,记为 x c c w
整理可得静水总压力的压心位置: yD yc
dP ghdw gy sin dw
P dP gy sin dw
w w
P dP
O (b) α h C dw M(x,y) C D YC
hc
D
g sin ydw
w
y
x
其中 为平面对Ox轴的面积矩 P g sin yc w ghc w 所以静水总压力的大小为
1 0.1 12h 6
得
4 h m 3
第二章 水静力学
【例题】一垂直放置的圆形平板闸
门如图所示,已知闸门半径R=1m, 形心在水下的淹没深度hc=8m,试用 解析法计算作用于闸门上的静水总压 力。 解:
R4pc w ghc R2 9.8 8 12 246kN
水静力学的主要内容
§2-1 静水压强 §2-2 静水压强的分布规律 §2-3 作用在平面上的静水总压力 §2-4 作用在曲面上的静水总压力
习题课2:压强分布图,压力体,平面板,曲面版总压力计算.ppt

h2
FP
b
(h2
h1) ( gh1
2
gh2 )
b
117.6kN
F
b
1 2
g(h1
h2 ) (h1
h2 ) b
39.2kN
方向向右
F b g(h1 h2 ) h2 b 78.4kN
依力矩定理:
FP e F
[h2
(h1
3
h2
)
]
F
h2 2
可解得:e=1.56m
答:略
压力体绘制
画出下图边壁上的静水压强分布图
(H h)
H
H
1
1 H
2
(H h)
H 1H
1
(H H )
1
2
(H h)
(H H H )
1
2
3
例题补充:
一垂直放置的圆形平板闸门如
图所示,已知闸门半径R=1m,形心 在水下的淹没深度hc=8m,试用解析
hD hc
法计算作用于闸门上的静水总压力。 FP
静水总压力。 解:闸门前水深为 h R sin 2 sin 45 1.414m
A
h D
O φ
ZD
αR
B
水平分力: 铅直分力:
FPx
FPz
pc Ax
gV
gghc(A1xR92.811.h421h4)b1.42124.344kN39.19kN
8
2
静水总压力的大小: FP FP2x FP2z 45.11kN
h1/3
该闸门上所受到的静水总压力。
e
h2/3 h2
解法一:首先分别求出两侧的水压力,然后求合力。
FP左
拓展资料:压强的计算(高中物理教学课件)完整版3
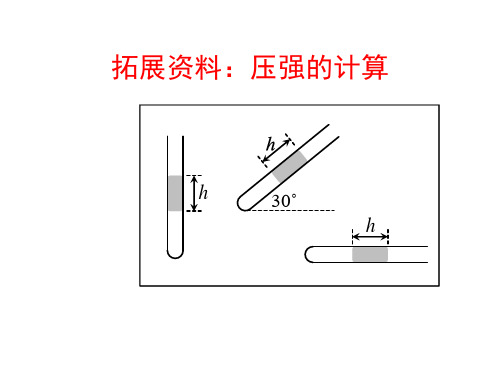
gh
注意: ①密封气体内部包括与液面接触外压强处处相同 ②上面压强单位是Pa,如果用cmHg表示压强有时也写成: p=p0+h或者p=p0-h的形式,比如60cmHg,甚至1.2atm
一.压强的计算 设外界大气压强为p0,玻璃管横截面积为S,求下 面几种情况下被密封气体的压强p。
h 等价
h
12
3
h 等价 3 h
答:pA=65cmHg, pB=60cmHg
典型例题
例3.求下列两种水银槽内被密封气体的压强,已 知外界大气压为p0=76cmHg。
a
10cm
b
5cm
答:pa=66cmHg, pb=81cmHg
典型例题
例4.将一根质量可以忽略的一端封闭的塑料管子 插入液体中,在力F的作用下保持平衡,如图所 示,图中H值的大小与下列各量无关的是 ( B ) A.管子的半径 B.大气压强 C.液体的密度 D.力F
12
1
利用连通器原理液体在同一深度处压强大小相同可知1位 置和2位置压强大小相等,等价于求3位置的压强。
p
p0
mg S
p0
gh
p
p0
mg S
p0
gh
一.压强的计算 设外界大气压强为p0,玻璃管横截面积为S,求下 面几种情况下被密封气体的压强p。
等价
1 h2
3h
等价
1 h2
2h
3
利用连通器原理液体在同一深度处压强大小相同可知1位 置和2位置压强大小相等,等价于求3位置的压强。
答:0.9l0
典型例题
例10.如图所示,一汽缸水平固定在静止的小车上,一质 量为m,面积为S的活塞将一定量的气体封闭在汽缸内, 平衡时活塞与汽缸底相距为L。现让小车以一较小的水平 恒定加速度向右运动,稳定时发现活塞相对于汽缸移动 了距离d。已知大气压强为p0,不计汽缸和活塞间的摩擦; 且小车运动时,大气对活塞的压强仍可视为p0;整个过 程温度保持不变。求小车加速度的大小。
工程流体力学1-5章习题解答

第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τ Pa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]1-6.为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。
压力压强(三)------对容器底部的压强压力与对桌面的压强压力计算

压力压强--两种压强压力的计算专题一:容器中液体对容器底部的压强压力计算。
解题思路:因为容器底部是被液体压着的,所以去求液体对容器底部的压强与压力时,应该用液体压强公式P=ρ液gh先算压强,再利用固体压强的变形公式F=PS去计算液体对容器底的压力。
步骤一:先求压强,利用公式P=ρ液gh步骤二:再求压力,利用公式F=PS专题二:容器对水平桌面的压强压力计算。
解题思路:容器放在水平桌面上,容器中的液体压在容器上,所以容器对水平桌面的压力求解对桌面的压强。
大小应该等于容器的重力加上液体的重力:F=G总=G液+G容。
再利用P=FS步骤一:先算压力,利用公式F=G液+G容步骤二:再算压强,利用公式P=FS练习题一.选择题1.(多选)小强将一只质量为1kg的平底水桶放在水平地面上,如图所示。
已知该水桶的底面积为5×10-2m2,桶内装有50cm深的水,水对桶底的压力比桶对地面的压力小40N,g取10N/kg。
下列判断中正确的是()A. 水对桶底的压强为5×105PaB. 水对桶底的压力为250NC. 桶对地面的压力为290ND. 桶内水的质量为28kg2.如图所示,玻璃杯里有3N的4℃的水(密度ρ水=1g/cm3),水的深度为10cm,玻璃杯重0.6N,玻璃杯底面积为20cm2(杯的厚度可以不计),g取10N/kg。
已知水在4℃时密度最大,不考虑玻璃杯的热胀冷缩,以及水的物态变化,则当水温从0℃逐渐升高到10℃的过程中()A. 水对杯底的压强可能是1001PaB. 杯子对桌面的压强始终是1500PaC. 杯子对水面的高度可能是9.9cmD. 水对杯底的压力一定先增大后减小3.如图所示,盛有水的平底紫砂壶静止在水平桌面上。
壶重1N ,高9cm ,底面积为30cm 2;壶内水重2N ,水深6cm ,水的密度为331.010kg/m ⨯ ,g 取10N/kg 。
下列选项中正确的是( )A. 水对壶底的压力为2NB. 水对壶底的压强为900PaC. 紫砂壶对桌面的压力为2.8ND. 紫砂壶对桌面的压强为1000Pa4.如图11所示,盛有水的杯子静止在水平桌面上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3
h2
)
]
FX
h2 2
可解得:e=1.56m
答:略
压力体绘制
A
B
C D
A
B C
D
❖ 压力体的绘制(一):
❖ 压力体的绘制(二):
压力体
压力体绘制
FPz
C
A
FPx
压强计算
FPx
D
FPz
B
请注意区分:压强分布图和压力体的画法和应用
压强分布图
压强分布图
相互抵消 Px=0
压力体:
例题补充: 一弧形闸门如图所示,闸门宽度b=4m,圆心角φ=45°,
宽b=2m,一侧水深h1=4m,另 h1
一侧水深h2=2m,试用图解法求
h1/3
该闸门上所受到的静水总压力。
e
h2/3 h2
解法一:首先分别求出两侧的水压力,然后求合力。
FP左
左b
1 2
gh1h1b
1 2
10009.8 4
42
156800N
156.8kN
FP右 合 力右对b 任 12一轴gh的2h力2b矩等12 于1各00分0力9对.8 2 2 2 39200N 39.2kN
解:静水压力的计算
H R sin 30 10 0.5 5m
水平分力的计算
Px
hc
Ax
(4
H 2
) (bH )
9.8 (4 5)58 2548KN 2
静水总压力的铅直分力的计算 ab R Rcos30o 10 100.866 1.34m
Pz V Aabcdeb (A矩形abve A扇形eod A三角形cod) b
h1
e
h2
FP
b
(h2
h1) ( gh1
2
gh2 )
b
117.6kN
FV
Vb
1 2
g (h1
h2
)
(h1
h2 )
b
39.2kN
方向向右
FX Xb g(h1 h2 ) h2 b 78.4kN
依力矩定理:
FP
e
FV
[h2
(h1
画出下图边壁上的静水压强分布图
Hale Waihona Puke (H h)HH
1
1 H
2
(H h)
H 1H
1
(H H )
1
2
(H h)
(H H H )
1
2
3
例题补充:
一垂直放置的圆形平板闸门如
图所示,已知闸门半径R=1m,形心 在水下的淹没深度hc=8m,试用解析
hD hc
半径R=2m,闸门旋转轴恰与水面齐平。求水对闸门的
静水总压力。 解:闸门前水深为 h R sin 2 sin 45 1.414m
A
h D
O φ
ZD
αR
B
水平分力: 铅直分力:
FPx
FPz
pc Ax
gV
gghc(A1xR92.811.h421h4)b1.42124.344kN39.19kN
法计算作用于闸门上的静水总压力。 FP
解: FP pc A ghc R2 246kN
R4
LD
LC
IC LC
A
hC
4 hC
A
8.03m
答:该闸门上所受静水总压力的大小为246kN,方向向右, 在水面下8.03m处。
例题补充:
如图所示,某挡水矩形闸门,门
压力中心D
h D 4 10 sin16.91 6.91m
静水总压力为2663KN;合力作用线与水平 方向的夹角为16.91°,合力与闸门的交点到 水面的距离6.91米。
FP 该F轴P左力矩FP的右 代 1数5和6.8。 39.2 117.6kN 方向向右→
依力矩定理:
FP
e
FP左
h1 3
FP右
h2 3
可解得:e=1.56m
答:该闸门上所受的静水总压力大小为117.6kN,方向向右,作
用点距门底1.56m处。
解法二:首先将两侧的压强
分布图叠加,直接求总压力
(4
1.34
30 360
102
1 2
5
8.66)
9.8
8
774.6KN
静水总压力
P Px2 Py2 25482 774.12 2663KN
合力与水平线的夹角
tg 1( pz ) tg 1( 774.6) 16.91o
px
2548
8
2
静水总压力的大小: FP FP2x FP2z 45.11kN
静水总压力与水平方向的夹角:
arctan
FPz FPx
29.68
静水总压力的作用点:ZD R sin 2 sin 29.68 1m
答:略。
例题4: 如图所示为一溢流坝上的弧形门。已 知:R=10m,门宽b=8m,α=30ο,试求:作用 在弧形闸门上的静水总压力及其作用线位置。
