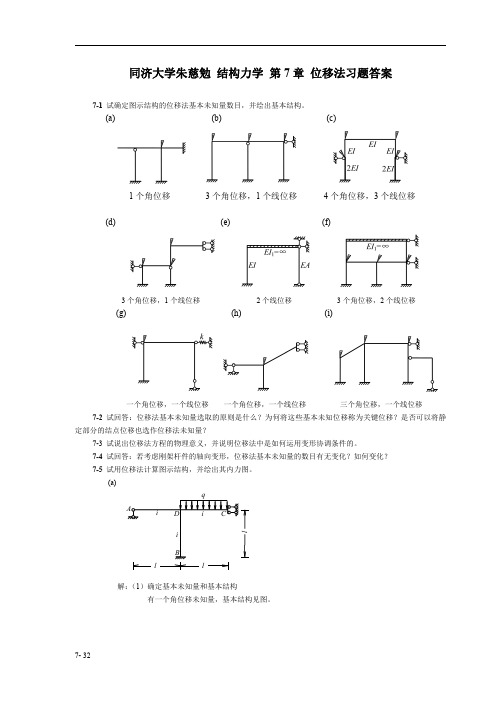
第七章位移法(选择填空题)
第七章位移法复习材料

第七章位移法【练习题】7-1是非题:1、位移法未知量的数目与结构的超静定次数有关。
2、位移法的基本结构可以是静定的,也可以是超静定的。
3、位移法典型方程的物理意义反映了原结构的位移协调条件。
4、结构按位移法计算时,其典型方程的数目与结点位移数目相等。
5、位移法求解结构内力时如果M P图为零,则自由项R IP一定为零。
6、超静定结构中杆端弯矩只取决于杆端位移。
7、位移法可解超静定结构,也可解静定结构。
8、图示梁之EI =常数,当两端发生图示角位移时引起梁中点C之竖直位移为(3/8)1 (向下)。
l /2l /29、图示梁之EI=常数,固定端A发生顺时针方向之角位移,由此引起铰支端B之转角(以顺时针方向为正)是-/210、用位移法可求得图示梁B端的竖向位移为ql3/24EI。
| H I八H M H仏A ELB -11、图示超静定结构,D为D点转角(顺时针为正),杆长均为I , i为常数。
此结构.. 2可写出位移法方程11i D ql /12 0 。
7-2选择题:1、位移法中,将铰接端的角位移、滑动支承端的线位移作为基本未知量:A、绝对不可;B、必须;C、可以,但不必;D、一定条件下可以。
2、AB杆变形如图中虚线所示,则A端的杆端弯矩为:A. M AB 4i A 2i B 6i AB/I ;B. M AB 4i A 2i B 6i AB /1 ;C.M AB 4i A 2i B 6i AB / | ;D. M AB 4i A 2i B 6i AB /1。
A3、图示连续梁,已知P ,l, B , C ,贝U:A M BC4i B4i C;B M BC4i B2i C・C . M BC4i B PI / 8;D . M BC4i B PI /8 。
4、图示刚架,各杆线刚度i相同,则结点A的转角大小为:A . m o /(9i ) ;B . m °/(8i );C . m )/(11 i ) ;D . m o /(4 i ) o5、图示结构,其弯矩大小为:A . M AC ==Ph /4, M BD = =Ph /4 ;B . M AC = :Ph /2, M BD =Ph /4 ;C . M AC ==Ph /4, M BD = =Ph /2 ; D . M AC : =Ph /2, M BD = = Ph /2。
结构力学-第7章-位移法习题答案
1 2
ql
1 12
ql 2
/ l
7 12
ql
由位移法方程得出:
r11Z1
R1 p
0
Z1
7ql 4 348EI
作出最终 M 图
7-9 试不经计算迅速画出图示结构的弯矩图形。
(a)
B
θA A
(b)
C B
yB
B′
A
C
题 7-9 图 7-10 试计算图示有剪力静定杆的刚架,并绘出 M 图。
13EI l
, r12
r21
3EI l2
r22
18EI l2
R1 p
1 16
ql 2 , R2 p
ql
代入,解得
Z1
66 3600
ql3 EI
,
Z2
211 3600
ql 4 EI
(4)求最终弯矩图
(e)
50kN·m
80kN·m 10kN·m 20kN
A 2EI B EI C
EI
(b)
B
3EI
C
EI
EI
A
D
Δ l
l
解:(1)求 M1, M 2 , M 3, M p 图。
(2)由图可知:
r11
16i, r12
r21
6i, r23
r32
6i l
, r22
16i, r33
24i l
R1 p
0, R2 p
位置位移练习题

位置位移练习题一、选择题1. 位移是描述物体位置变化的物理量,其方向是由起点指向终点。
以下哪个选项正确描述了位移的特点?A. 位移是标量,只有大小没有方向B. 位移是矢量,有大小和方向C. 位移的大小等于物体运动的路程D. 位移的大小等于物体运动的时间2. 物体从A点移动到B点,再从B点返回A点,其位移大小为:A. 0B. 从A到B的距离C. 从B到A的距离D. 从A到B再从B到A的总距离3. 以下哪个选项正确描述了路程和位移的区别?A. 路程是物体实际走过的路径长度,位移是物体位置变化的物理量B. 路程和位移是同一个概念C. 路程是矢量,位移是标量D. 路程是标量,位移是矢量二、填空题4. 位移的大小等于首末位置的距离,用公式表示为:\( \text{位移} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \),其中 \( x_1, y_1 \) 是起始位置的坐标,\( x_2, y_2 \) 是末位置的坐标。
5. 如果物体沿直线从A点到B点,再从B点到C点,那么物体的总位移是\( \text{AB} + \text{BC} \),但总路程是\( \text{AC} \)。
三、计算题6. 一个物体从坐标原点出发,先向东移动了3米,然后向北移动了4米。
求物体的位移大小和方向。
7. 物体从A点出发,先向西移动了5米到达B点,再向南移动了6米到达C点。
如果物体最终返回到A点,求物体的总位移大小。
四、简答题8. 解释为什么位移和路程在某些情况下可以不同,并给出一个实际的例子。
9. 描述在二维平面上,如果物体沿直线从一点移动到另一点,其位移和路程是否相等,并解释原因。
五、应用题10. 一个运动员在田径场的跑道上跑了一个400米的圈,求运动员的总路程和位移大小。
11. 假设有一个点光源,一个物体从光源的正东方向移动到正西方向,移动了10米,然后从正西方向返回到正东方向,再移动了5米。
结构力学习题集-矩阵位移法习题及答案
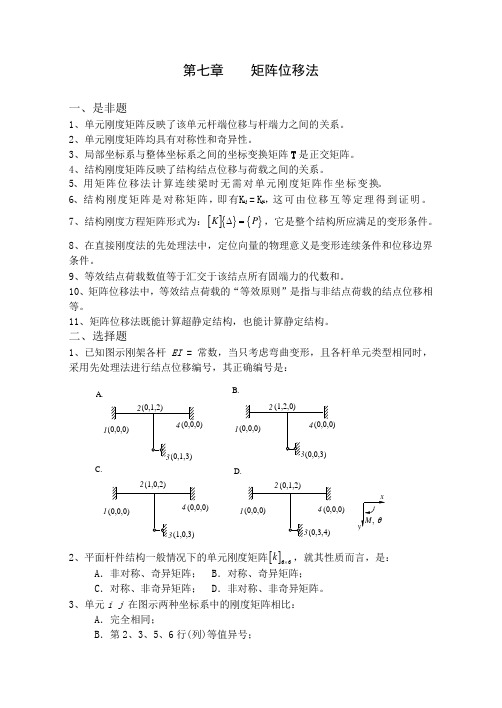
第七章 矩阵位移法一、是非题1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。
2、单元刚度矩阵均具有对称性和奇异性。
3、局部坐标系与整体坐标系之间的坐标变换矩阵T 是正交矩阵。
4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。
5、用 矩 阵 位 移 法 计 算 连 续 梁 时 无 需 对 单 元 刚 度 矩 阵 作 坐 标 变 换。
6、结 构 刚 度 矩 阵 是 对 称 矩 阵 ,即 有K i j = K j i ,这 可 由 位 移 互 等 定 理 得 到 证 明 。
7、结构刚度方程矩阵形式为:[]{}{}K P ∆=,它是整个结构所应满足的变形条件。
8、在直接刚度法的先处理法中,定位向量的物理意义是变形连续条件和位移边界条件。
9、等效结点荷载数值等于汇交于该结点所有固端力的代数和。
10、矩阵位移法中,等效结点荷载的“等效原则”是指与非结点荷载的结点位移相等。
11、矩阵位移法既能计算超静定结构,也能计算静定结构。
二、选择题1、已知图示刚架各杆EI = 常数,当只考虑弯曲变形,且各杆单元类型相同时,采用先处理法进行结点位移编号,其正确编号是:(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.21341234123412342、平面杆件结构一般情况下的单元刚度矩阵[]k 66⨯,就其性质而言,是: A .非对称、奇异矩阵; B .对称、奇异矩阵; C .对称、非奇异矩阵; D .非对称、非奇异矩阵。
3、单元i j 在图示两种坐标系中的刚度矩阵相比:A .完全相同;B .第2、3、5、6行(列)等值异号;C .第2、5行(列)等值异号;D .第3、6行(列)等值异号。
xi4、矩阵位移法中,结构的原始刚度方程是表示下列两组量值之间的相互关系: A .杆端力与结点位移; B .杆端力与结点力; C .结点力与结点位移; D .结点位移与杆端力 。
《结构力学习题集》(下)-矩阵位移法习题及答案 (2)

第七章 矩阵位移法一、就是非题1、单元刚度矩阵反映了该单元杆端位移与杆端力之间得关系。
2、单元刚度矩阵均具有对称性与奇异性。
3、局部坐标系与整体坐标系之间得坐标变换矩阵T 就是正交矩阵。
4、结构刚度矩阵反映了结构结点位移与荷载之间得关系。
5、用 矩 阵 位 移 法 计 算 连 续 梁 时 无 需 对 单 元 刚 度 矩 阵 作 坐 标 变 换。
6、结 构 刚 度 矩 阵 就是 对 称 矩 阵 ,即 有K i j = K j i ,这 可 由 位 移 互 等 定 理 得 到 证 明 。
7、结构刚度方程矩阵形式为:,它就是整个结构所应满足得变形条件。
8、在直接刚度法得先处理法中,定位向量得物理意义就是变形连续条件与位移边界条件。
9、等效结点荷载数值等于汇交于该结点所有固端力得代数与。
10、矩阵位移法中,等效结点荷载得“等效原则”就是指与非结点荷载得结点位移相等。
11、矩阵位移法既能计算超静定结构,也能计算静定结构。
二、选择题1、已知图示刚架各杆EI = 常数,当只考虑弯曲变形,且各杆单元类型相同时,采用先处理法进行结点位移编号,其正确编号就是:(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.21341234123412342、平面杆件结构一般情况下得单元刚度矩阵,就其性质而言,就是:A.非对称、奇异矩阵;B.对称、奇异矩阵;C.对称、非奇异矩阵;D.非对称、非奇异矩阵。
3、单元i j 在图示两种坐标系中得刚度矩阵相比:A.完全相同;B.第2、3、5、6行(列)等值异号;C.第2、5行(列)等值异号;D.第3、6行(列)等值异号。
4、矩阵位移法中,结构得原始刚度方程就是表示下列两组量值之间得相互关系:A.杆端力与结点位移;B.杆端力与结点力;C.结点力与结点位移;D.结点位移与杆端力。
位移 位移定理练习题

位移位移定理练习题位移定理练题位移定理是力学中的一个重要原理,在求解物体运动时经常会用到。
下面是一些位移定理的练题,以帮助你加深对该原理的理解。
题目一一辆汽车以匀速行驶,速度为25 m/s。
如果它在10秒内行驶的距离为多少?根据位移定理,位移(s)等于速度(v)乘以时间(t)。
因此,s = v × t = 25 × 10 = 250m。
答案:位移为250米。
题目二一架飞机以加速度2 m/s²匀加速起飞。
如果飞机起飞所经过的距离为800米,求起飞所用的时间。
根据位移定理,位移(s)等于初速度(v₀)乘以时间(t)加上加速度(a)的一半乘以时间的平方。
因此,s = v₀t + (1/2)at²。
已知v₀ = 0(起始速度为0),a = 2 m/s²,s = 800米。
代入上述公式,800 = 0 × t + (1/2) * 2 * t²。
化简得到2t² = 800,解得t = √(800/2) ≈ 20。
答案:起飞所用的时间为20秒。
题目三一个物体从静止开始匀加速运动,经过4秒钟位移为40米。
求该物体的加速度。
根据位移定理,位移(s)等于初速度(v₀)乘以时间(t)加上加速度(a)的一半乘以时间的平方。
因此,s = v₀t + (1/2)at²。
已知v₀ = 0(起始速度为0),s = 40米,t = 4秒。
代入上述公式,40 = 0 × 4 + (1/2) * a * 4²。
化简得到4a = 40,解得a = 40/4 = 10。
答案:物体的加速度为10 m/s²。
题目四一个物体以初速度10 m/s匀减速运动,经过5秒钟位移为30米。
求该物体的加速度。
根据位移定理,位移(s)等于初速度(v₀)乘以时间(t)减去加速度(a)的一半乘以时间的平方。
因此,s = v₀t - (1/2)at²。
位移法复习题

位移法复习题位移法复习题位移法是力学中的一种重要方法,用于求解物体在受力作用下的运动情况。
它通过分析物体的位移来推导出物体的速度和加速度等运动参数。
在学习位移法时,我们需要掌握一些基本的概念和方法,并通过练习题来加深理解。
下面,我们将通过一些典型的位移法复习题来巩固知识。
1. 一辆汽车以20 m/s的速度匀速行驶了5秒钟,求汽车的位移。
解析:根据位移的定义,位移等于速度乘以时间。
所以汽车的位移等于20 m/s × 5 s = 100 m。
2. 一个物体以2 m/s²的加速度匀加速运动了10秒钟,求物体的位移。
解析:根据匀加速运动的位移公式,位移等于初速度乘以时间加上加速度乘以时间的平方的一半。
所以物体的位移等于0 m/s × 10 s + 2 m/s² × (10 s)² / 2 = 100 m。
3. 一个自由落体物体从静止开始下落,求物体下落5秒钟后的位移。
解析:自由落体物体的加速度等于重力加速度,即9.8 m/s²。
根据自由落体运动的位移公式,位移等于初速度乘以时间加上加速度乘以时间的平方的一半。
由于物体从静止开始下落,所以初速度为0 m/s。
所以物体的位移等于0 m/s × 5 s + 9.8 m/s² × (5 s)² / 2 = 122.5 m。
4. 一个物体以10 m/s的速度向上抛出,求物体到达最高点时的位移。
解析:当物体到达最高点时,它的速度为0 m/s。
根据物体的运动规律,物体到达最高点时的位移等于它的初速度乘以时间。
所以物体到达最高点时的位移等于10 m/s × (10 m/s / 9.8 m/s²) = 10.2 m。
5. 一个物体以5 m/s的速度向上抛出,求物体落地时的位移。
解析:当物体落地时,它的位移等于它的初速度乘以时间加上加速度乘以时间的平方的一半。
第7章位移法

φA P q MAB A φA βAB QAB QBA l t1˚C βAB EI t2˚C φB B ΔAB
B'
MBA
EI EI EI f M AB 4 A 2 B 6 2 Δ M AB l l l M 2 EI 4 EI 6 EI Δ M f A b BA BA l l l2 Q 6EI 6EI 12EI Δ Q f a b AB AB l2 l2 l3 6EI 6EI 12EI f Q AB 2 a 2 b 3 Δ QBA l l l
EI 4EI (2i)
E
2kN/m
C
ø B
B
ø B
所以: k11 △ 1 +F1P=0
△ 1= ø B
△ 1=- F1P/ k11
C A C
△ 1= 1
(c)
A
ø B
F11 ø B B F1P q
ø B
k11
B
ø B
C
(d)
A
B
观察3位移法基本思路
q
↓↓↓↓↓↓↓↓↓↓
↓↓↓↓↓↓↓↓↓↓
F1
q
↓↓↓↓↓↓↓↓↓↓ ql2/12
第7章
4、解方程,求得
8i1 2i 2 22 .5 0 2i1 7i 2 45 0
1 4.76i 2 7.79i
5、按M=M1X1+ M2X2+ MP绘弯矩图
例7-2 用位移法求图示刚架的M图,各杆EI 相同。 解: 8kN/m B
i
D
i
E
点击左键,一步步播放。结束播放请点“后退”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
17、位移法典型方程中的系数是:( )
A.单位位移引起的杆端力或杆端弯矩;
B.单位位移引起的附加联系的反力或反力矩;
C.单位荷载引起的杆端力或杆端弯矩;
D.单位荷载引起的附加联系的反力或反力矩。
18、在位移法中,将铰接端的角位移、滑动支承端的线位移作为基本未知量:
()A. 绝对Biblioteka 可;B. 一定条件下可以;
P
AB
CD
i
i
i
l/2 l/2 l
l
12、 位移法的适用范围:( ) A. 不能解静定结构; B.只能解超静定结构; C. 只能解平面刚架; D.可解任意结构。
13、位移法解图a所示的结构内力时,若取图b为基本结构,则主系数r11的值为: ()
A. 4i ; B. 6i ; C. i ; D. 10i 。
120
M A
23、图示结构(EI=常数)用位移法求解的基本未知量数目为___个。
M
P3
24、图示各结构 E I,E A 为常数,用位移法求解时,基本未知量数目最少为:角位
移
___个, 线位移
个。
121
A.9EI/l; B. 10EI/l; C. 11EI/l; D. 7EI/l。
q
EI A
2EI
l
EI
l
l
4、 图示结构,MBA为:( ) A.0.5pl; B. 0.75pl; C.0.25pl; D. -0.25pl。
117
EI=∞
A
P
EI
EI
l
l
B
5、在位移法典型方程中。系数γi j(i≠j )的物理意义可叙述为: ( ) A. 附加约束i发生Zi=1 在附加约束i上产生的反力或反力矩; B. 附加约束i发生Zi=1 时在附加约束j上产生的反力或反力矩; C. 附加约束j发生Zi=1 时在附加约束i上产生的反力或反力矩; D.附加约束j发生Zi=1 时在附加约束j上产生的反力或反力矩。( )
第七章 位移法
(选择、填空题)
1、图示结构各杆 EI 为常数,其结点位移基本未知量为_______ A.1; B. 2; C.3; D.4。
2、图示结构位移法基本方程的系数k11= __________EI/l 。 A.18; B. 16; C.15; D.17。
l
l
2EI 2EI
2EI
l
3、图示结构用位移法计算时,若取结点 A 的转角为Z1,γ11为( )
6、在位移法典型方程的系数和自由项中,数值范围可为正、负实数的有:
()
A.主系数;
B.主系数和副系数;
C.主系数和自由项;
D.副系数和自由项。
7、 用位移法计算刚架,常引入轴向刚度条件,即“受弯直杆在变形后两端距离保
持不变”。此结论是由下述假定导出的: ( )
A. 忽略受弯直杆的轴向变形和剪切变形;
Pl/4
Pl/4
l
20、表示杆件杆端力和杆端位移之间关系的方程为杆件的______方程。 21、系数ki j =kj i 是由________定理得到的结果。 22、图示结构各杆的长度 l 和 EI 相同,若在结点 A 施加的力矩 M=______________ 时,结点 A 将产生单位顺时针之角位移。
C. 可以,但不必;
D. 必须。
19、 图 b 是图 a 所示结构位移法所作图的条件是: ( )
A. i1=i2=i3 ,为有限值; B. i1≠i2, i1=i3 ,为有限值; C. i1≠i2≠i3 ,为有限值; D. i2=∞ ,i1=i3,为有限值。
(a) i2
(b) Pl/4
Pl/4
i1
i3 l
B. 弯曲变形是微小的;
C.变形后杆件截面仍与变形曲线相垂直;
D. 假定 A 与 B 同时成立。
8、用位移法计算图示结构的基本未知数数目是:( )
A. 4 ; B.5 ;C. 6 ; D. 7 。
9、计算刚架时,位移法的基本结构是: ( )
A.超静定铰结体系;
B. 单跨超静定梁的集合体;
C.单跨静定梁的集合体; D. 静定刚架。
Z1 i1
2i
14、用位移法计算图示结构内力时,基本未知量数目为:( ) A. 1 ; B. 2 ; C.3 ; D.4 。
A
15、用位移法计算图示结构内力时,基本未知量数目为 : ( ) A. 1 ; B. 2 ; C.3 ; D.4 。
P AB
119
16、用位移法计算图示结构内力时,基本未知量数目为:( ) A.1 ; B. 2 ; C.3 ; D. 4 。
10、位移法典型方程中主系数r11一定为: ( )
A. 等于零; B.大于零; C.小于零; D.大于等于零。
11、图示连续梁,已知P , l,ϕBB , ϕC,则:( )
118
A.MBC= 4iϕBB +4iϕC ; C. MBC= 4iϕBB +Pl/8 ;
B. MBC= 4iϕBB +2iϕC ; D. MBC= 4iϕBB -Pl/8 。
