矩阵乘积的逆(高等代数课件)
合集下载
线性代数之——矩阵乘法和逆矩阵
线性代数之——矩阵乘法和逆矩阵1. 矩阵乘法如果矩阵 B 的列为 b 1,b 2,b 3，那么 EB 的列就是 Eb 1,Eb 2,Eb 3。
EB =E [b 1b 2b 3]=[Eb 1Eb 2Eb 3]E (B 的第 j 列)=EB 的第 j 列置换矩阵（permutation matrix ）在消元的过程中，如果遇到了某⼀⾏主元的位置为 0，⽽其下⾯⼀⾏对应的位置不为 0，我们就可以通过⾏交换来继续进⾏消元。
如下的矩阵 P 23 可以实现将向量或者矩阵的第 2 、 3 ⾏进⾏交换。
P 23=10000101100001010135=15310000101241003065=24106503置换矩阵 P ij 就是将单位矩阵的第 i ⾏和第 j ⾏进⾏互换，当交换矩阵乘以另⼀个矩阵时，它的作⽤就是交换那个矩阵的第 i ⾏和第 j ⾏。
增⼴矩阵（augmented matrix ）在消元的过程中，⽅程两边的系数 A 和 b 都要进⾏同样的变换，这样，我们可以把 b 作为矩阵 A 的额外的⼀列，然后，就可以⽤消元矩阵E 乘以这个增⼴的矩阵⼀次性完成左右两边的变换。
E [A b ]=[EA E b ]100−2100124−2249−38−2−3710=24−220114−2−3710矩阵乘法的四种理解如果矩阵 A 有 n 列， B 有n ⾏，那么我们可以进⾏矩阵乘法 AB 。
假设矩阵 A 有 m ⾏ n 列，矩阵 B 有 n ⾏ p 列，那么 AB 是 m ⾏ p 列的。
(m ×n )(n ×p )(m ×p )m ⾏n 列n ⾏p 列m ⾏p 列矩阵乘法的第⼀种理解⽅式就是⼀个⼀个求取矩阵 AB 位于 (i ,j ) 处的元素(AB )ij =A 的第 i ⾏与 B 的第 j 列的内积=∑a ik b kj第⼆种理解，矩阵 AB 的列是 A 的列的线性组合AB =A [b 1b 2⋯b p ]=[Ab 1Ab 2⋯Ab p ]第三种理解，矩阵 AB 的⾏是 B 的⾏的线性组合[][][][][][][][][][][][][]AB=a1a2⋮a mB=a1Ba2B⋮a m B第四种理解，矩阵AB是所有A的列与B的⾏的乘积的和AB=[a1a2⋯a n]b1b2⋮b n=n∑i=1a i b i其中，⼀列乘以⼀⾏称为外积（outer product），(n×1)(1×n)=(n, n)，结果为⼀个 n×n 的矩阵。
高等数学第四章课件-矩阵的逆
( AB ) B −1 = EB −1 ,
例1 判断矩阵A是否可逆，若可逆，求其逆 . ⎛ 1 2 3⎞ (1) A = ⎜ 2 2 1 ⎟ ⎜ 3 4 3⎟ ⎝ ⎠ 1 2 3 −1 ∴ A 存在. 解: ∵ A = 2 2 1 = 2 ≠ 0, 3 4 3 2 1 2 1 2 2 A11 = = 2, A12 = − = −3, A13 = = 2, 3 3 3 4 4 3 同理可得, A21 = 6, A22 = −6, A23 = 2,
2 A − 3 A − 10 E = 0 相矛盾. 这与
所以, A + 2 E 与 A − 5 E 不同时可逆.
例2’’ 设方阵 A 满足 A2 − 3 A − 10 E = 0, 若 A ≠ 5 E , 证明: A + 2 E 不可逆. 证： （反证法） 假设A+2E可逆,
−1 2 ( A + 2 E ) ( A − 3 A − 10 E ) = 0 则 −1 即( A + 2 E ) ( A + 2 E )( A − 5 E ) = 0
⎛ A1 (3) 设 A1 , A2 是 n1 , n2 级可逆矩阵, A = ⎜ ⎝ A3 解: 因为 A1 , A2可逆
0⎞ ⎟. A2 ⎠
A1 ∴| A |= A3
0 =| A1 || A2 |≠ 0. A2
故A可逆. ⎛ X 11 −1 设A =⎜ ⎝ X 21 ⎛ A1 则 ⎜ ⎝ A3
⇒ B = 6( A − E ) .
−1 −1
B = 6( A − E )
−1
−1
⎡⎛ 2 ⎜ ⎢ = 6 ⎜0 ⎢ ⎜0 ⎢ ⎣⎝
0 4 0
ห้องสมุดไป่ตู้
高等数学逆矩阵ppt课件
268.
例7: 设方阵A满足矩阵方程 A2–A–2E = O, 证明: A, A+2E 都可逆, 并求它们的逆矩阵.
证明: 由 A2–A–2E=O, 得 A(A–E)=2E,
则
A
1
(
A
E
)
A1 E,
故A可逆, 且A-1 = 1 ( A E ).
2
2
又由 A2–A–2E=O, 得 (A+2E)(A–3E)+4E=O,
1 3
2, A12
2 3
1 3
3, A13
2 3
2 4
2,
同理可得 A21 6, A22 6, A23 2,
A31 4, A32 5, A33 2. 所以,
A
2 3
2
6 6
2
4 5
,
2
故
A1
|
1 A A|
1 3
1
2
3 3
1
5
122.
7
例3: 下列矩阵A,B是否可逆? 若可逆, 求其逆矩阵.
由伴随矩阵的性质: AA*= A*A = | A | E, 知
当| A | 0时,
A 1 A 1 A A E, | A| | A|
按逆矩阵的定义得, A1
1
A .
| A|
当| A | = 0 时, 称A为奇异矩阵, 否则称A为非奇异
矩阵.
4
由此可得, A是可逆矩阵的充分必要条件是A为非 奇异矩阵.
§2.3 逆 矩 阵
一、逆矩阵的概念和性质
在数的运算中, 当数 a 0 时, 有 aa-1 = a-1a = 1.
其中 a1 1 为a 的倒数, 或称a的逆(元). a
高等代数3-3矩阵的逆
... 0 A En ... A
A A
*
A11 A12 A 1n
A21 A22 A2 n
... An1 a11 ... An 2 a 21 ... Ann a n1
a12 a 22 an2
即矩阵A的逆矩阵是唯一的 .
B1 B1 E B1 ( AB2 ) ( B1 A )B2 EB2 B2
由于A的逆矩阵是唯一的，将A的唯一的逆矩阵记为 A1
则有
AA1 A1 A E
3. 单位矩阵E是可逆矩阵,且E 1 E .
4. 零矩阵O不是可逆矩阵.
a1 0 ... 0 0 a2 ... 0 例A 0 0 ... a n 其中 a1a2 ...an 0 a1 0 0 a2 0 0
可逆
1 0 3 0 1 A 1 2 3 1 2 3 3
1
1 3 A 2 6
A 0
不可逆
用公式法求二阶矩阵的 逆矩阵非常方便 .
a b 1 d d 1 若A , 且 A 0, 则 A . A c a c d
已知方阵A满足A3 A2 4 A 5 E O ,则( A 2 E )1 ________.
A2 A 2 E
1 2 0 已知AB B A , 其中B 2 1 0 ,则( A E )1 __________. 0 0 2
( A E )( B E ) E ( A E )1 B E
1 ( A 2E ) 2 1 例5 已知方阵A满足A A 4 E O ,则( A E ) __________. 2
高等代数课件PPT之第4章矩阵
策中甲的得分矩阵，规定胜者得1分，败者得-1分， 平手各得零分
0
1
–1
–1
0
1
1
–1
0
石头 剪子 布
乙方
石头 甲
剪子 方
布
0 1 1 答案 : 1 0 1 .
1 1 0
2.矩阵的线性运算（矩阵加法、 数乘） （1）矩阵相等
定义 设有两个m×n矩阵
a11
A
a21
am1
a12 a22
am2
总利润:862.5元
C矩其(1阵中)定AA义c与Baaij 12B设11的a矩i1乘baa阵 1积12j22是a一Ai 2b个2 jmaaa×i 12j ssnm矩sa阵,bbiBs12b11sCj bbbi12sj22ascinki b.j kjmbbn12nn,
a m1 i
a1m,22,, m; aj ms1,2,bs,1n
矩阵,也就是一个数.
4 1 0
例8
求
矩
阵A
1 2
0 1
3 0
21与B
1
2
1
1 0 3
3的 1
乘 积AB.
4
解
4 1 0
C AB
1 2
0 1
3 0
1
2
1
2
1
1 0 3
3 1 4
14 01 32 11 11 01 30 13 10 0 3 31 14
24 11 0 2 21
30
32
34
利润矩阵
由已知得
B
15
17.5
20
1220.5
总3.问A利B题2333润80241W:10521的这2L18330销一C售天31560F8利内7B1106.润，O5 总最0322B2和A小5711是号1.22这275500..多55牛里 设9少仔为7A.？裤5A23915872778.05..65521432.5（
0
1
–1
–1
0
1
1
–1
0
石头 剪子 布
乙方
石头 甲
剪子 方
布
0 1 1 答案 : 1 0 1 .
1 1 0
2.矩阵的线性运算（矩阵加法、 数乘） （1）矩阵相等
定义 设有两个m×n矩阵
a11
A
a21
am1
a12 a22
am2
总利润:862.5元
C矩其(1阵中)定AA义c与Baaij 12B设11的a矩i1乘baa阵 1积12j22是a一Ai 2b个2 jmaaa×i 12j ssnm矩sa阵,bbiBs12b11sCj bbbi12sj22ascinki b.j kjmbbn12nn,
a m1 i
a1m,22,, m; aj ms1,2,bs,1n
矩阵,也就是一个数.
4 1 0
例8
求
矩
阵A
1 2
0 1
3 0
21与B
1
2
1
1 0 3
3的 1
乘 积AB.
4
解
4 1 0
C AB
1 2
0 1
3 0
1
2
1
2
1
1 0 3
3 1 4
14 01 32 11 11 01 30 13 10 0 3 31 14
24 11 0 2 21
30
32
34
利润矩阵
由已知得
B
15
17.5
20
1220.5
总3.问A利B题2333润80241W:10521的这2L18330销一C售天31560F8利内7B1106.润，O5 总最0322B2和A小5711是号1.22这275500..多55牛里 设9少仔为7A.？裤5A23915872778.05..65521432.5（
高等代数课件--第四章 矩阵§4.4 矩阵的逆
１．伴随矩阵 定义： 设Aij矩阵A=(aij)nn中元素aij的 代数余子式，矩阵
A11 A 12 A* A1 n A21 A22 A2 n An1 An 2 adj A Ann
称为A的伴随矩阵．
性质 若A为n级方阵，则AA*=A*A=|A|En。
§4.4
矩阵的逆
一、可逆矩阵的定义：
设A为n级方阵，若有n级方阵B，使
AB=BA=En B为A的逆矩阵. 则称A为一个可逆矩阵，
注：
① 对于n级矩阵A，如果存在n级矩阵B， 使得AB=E，则A是可逆矩阵吗？
1=E
．
二、可逆矩阵的判定、求法
且(AB) 1=B 1A1.
问题：3）能否推广到有限个的情况?
4) 若A可逆，则A可逆,且(A ) 1=(A1).
5) 若A可逆, 则A*可逆且(A*) 1 =A/|A
6) 若A可逆, 则Ak可逆，且(Ak) 1 =(A1)k. 注：当|A|0时，定义A0=E，Ak =( A1)k。 当A, B可逆时，A+B不一定可逆。
的 逆 矩 阵 , an
其 中 a i 0, i 1, 2, ..., n .
推论
设A,B为n级方阵, 若AB=E，则A, B都 可逆，且 A1=B， B1= A．
三、逆矩阵的性质
1) 若A可逆，则A1可逆，且(A1) 1=A,
2) 若A可逆,0,则A可逆,且(A) 1= 1A1. 3) 若A,B为n级可逆方阵,则AB可逆,
例3
设方阵A满足A2 3A 10E=0，证明：
A，A 4E都可逆,并求它们的逆矩阵． 解：因为A(A3E)=10E, 所以A可逆,且 A1=(A-3E)/10 又(A+E)(A4E)=6E ,所以A4E可逆,且 (A4E)1=(A+E)/6
A11 A 12 A* A1 n A21 A22 A2 n An1 An 2 adj A Ann
称为A的伴随矩阵．
性质 若A为n级方阵，则AA*=A*A=|A|En。
§4.4
矩阵的逆
一、可逆矩阵的定义：
设A为n级方阵，若有n级方阵B，使
AB=BA=En B为A的逆矩阵. 则称A为一个可逆矩阵，
注：
① 对于n级矩阵A，如果存在n级矩阵B， 使得AB=E，则A是可逆矩阵吗？
1=E
．
二、可逆矩阵的判定、求法
且(AB) 1=B 1A1.
问题：3）能否推广到有限个的情况?
4) 若A可逆，则A可逆,且(A ) 1=(A1).
5) 若A可逆, 则A*可逆且(A*) 1 =A/|A
6) 若A可逆, 则Ak可逆，且(Ak) 1 =(A1)k. 注：当|A|0时，定义A0=E，Ak =( A1)k。 当A, B可逆时，A+B不一定可逆。
的 逆 矩 阵 , an
其 中 a i 0, i 1, 2, ..., n .
推论
设A,B为n级方阵, 若AB=E，则A, B都 可逆，且 A1=B， B1= A．
三、逆矩阵的性质
1) 若A可逆，则A1可逆，且(A1) 1=A,
2) 若A可逆,0,则A可逆,且(A) 1= 1A1. 3) 若A,B为n级可逆方阵,则AB可逆,
例3
设方阵A满足A2 3A 10E=0，证明：
A，A 4E都可逆,并求它们的逆矩阵． 解：因为A(A3E)=10E, 所以A可逆,且 A1=(A-3E)/10 又(A+E)(A4E)=6E ,所以A4E可逆,且 (A4E)1=(A+E)/6
5.6矩阵乘积的行列式及矩阵的逆
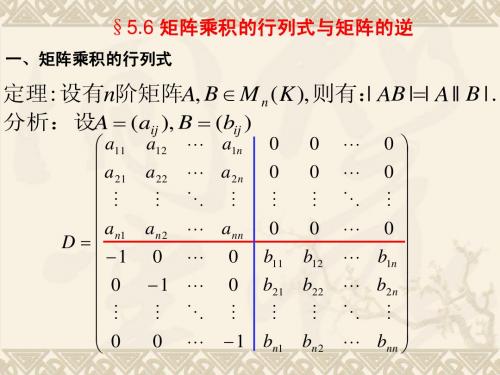
例4 解
1 求方阵 A 2 3
1 2 2 4 3 3 A 2 3 1
2 2 4
3 1 的逆矩阵. 3
2
A1存在.
又
6 4 2 A 3 6 5 , 2 2 2
3 2 6 4 1 2 1 1 故 A 1 A 3 6 5 3 2 3 5 2 . A 2 1 1 1 2 2 2
a a 解： A 11 12 , A* a22 a12 , a a a22 21 21 a11
A
1
1 1 * A a11a22 a12a21 | A|
a22 a 21
a12 . a11
例2: 单位矩阵E:
解 A =2, 11
A12 = 3 , A22 = 6 ,
A13 = 2 , A23 = 2 , A33 = 2 ,
所以:
6 4 2 A* 3 6 5 . 2 2 2
A21 = 6 ,
A31 = 4 , A32 = 5 ,
(2).用伴随矩阵求逆矩阵:
1 0 (A C) 2 0 1
1
例1：设 B
2
1 证明: A 可逆且 A 3E A . 1 3 2 1 2 证 A 3E A A A 2 2 2 3 1 2 E B E B 2 2
1
a 0, b 1, c 1, d 2.
a b B c d
BA
2 1 0 1 0 1 2 1 1 0 , 1 0 1 2 1 2 1 0 0 1
逆矩阵ppt课件
例 5 利用逆矩阵求解线性方程组
32xx11x22
x2
x3 3, 5x3 2,
3x1 2x2 3x3 1.
解
2 2 1
令
Hale Waihona Puke A3 31 2
53 ,
x1 3
则
A
x2
2
.
x3 1
7 4 9
由例2知，A1
6
3
3
7
,
2 4
x1
3 7 4 9 3 4
则
A21 A22 A23
A31
A32
A33
M11 M21 M31 7 4 9
M12
M 22
M 32
6
3
7
M13 M23 M33 3 2 4 10
例3
设
P
2 0
2
1
,
B
1 0
1 1
，且 AP PB, 求 An.
解：因| P | = 2，，则 P 可逆，且
A1
ad
1
bc
d c
b
a
9
2 2 1
例2
求3阶方阵
A
3
1
5
的逆矩阵.
3 2 3
解：| A | = 1， M11 7, M12 6, M13 3, M21 4, M22 3, M23 2, M31 9, M32 7, M33 4,
则
A1
|
1 A|
A*
A*
A11 A12 A13
证明： A2 3A 5E 0 ( A E)( A 4E) 9E 所以A + E 可逆，且
( A E)1 1 ( A 4E) 9
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§4.4 矩阵的逆
2. 逆矩阵的唯一性
若方阵 A 可逆，则其逆矩阵唯一 .
证明
有 于是
设 B 和 C 都是 A 的逆矩阵，则由定义
AB = BA = E，AC = CA = E，
B = BE = B( AC ) = ( BA )C = EC = C .
所以逆矩阵唯一.
证毕
§4.4 矩阵的逆
三、矩阵可逆的条件
d A.
立即可得,
a11 a12 a21 a22 * AA a a n1 n 2
a1n A11 A21 a2 n A12 A22 ann A1n A2 n
An1 An 2 Ann
§4.4
d 0 0 d 0 0 矩阵的逆
一、引例
引例 1 矩阵与复数
引例 2 坐标旋转变换 复数可以用二维有序数组来表示，如复数 a+bi
可表示为 (a , b) ，因此，从结构上看复数是矩阵的 引例 3 线性变换的逆变换 特殊情形 . 在第二节我们也看到，矩阵与复数相 在平面直角坐标系 xOy 中，将两个坐标轴同 仿，有加法、减法、乘法三种运算 . 我们知道，复 时绕原点旋转 角 ( 逆时针为正，顺时针为负 )， 设给定一个线性变换 数的乘法运算有逆运算，那么矩阵的乘法运算是否 就得到一个新的直角坐标系 (见图 3) ． 平面上 4 a– x , y1 a11 x1 a12 x2 1n n 也有逆运算呢？ 如果有的话，这种运算如何定义， Ｐ 任何一点 a21 x1 a22 x2 a2 n xn , y2 在两个坐标系中的坐标分别记为
称为A的伴随矩阵.
An1 An 2 Ann
性质： AA* A* A A E
§4.4 矩阵的逆
证：由行列式按一行（列）展开公式
ak 1 Ai 1 ak 2 Ai 2 a1l A1 j a2 l A2 j akn Ain d , k i 0, k i anl Anj d , l j 0, l j
. 1 an
§4.4 矩阵的逆
三、逆矩阵的运算规律
1 若A可逆, 则A 亦可逆, 且A
1 1 1
A.
2 若A可逆, 数 0, 则A可逆, 且
A A1 .
1
1
3 若A, B为同阶方阵且均可逆 , 则AB亦可逆, 且
A B 1 B 1 A 1
一、可逆矩阵的概念
定义 设A为n级方阵，如果存在n级方阵B，使得
AB＝BA＝E 则称A为可逆矩阵，称B为A的逆矩阵.
1 A . 注： ① 可逆矩阵A的逆矩阵是唯一的，记作
1 A ② 可逆矩阵A的逆矩阵 也是可逆矩阵，且
A
1
1
A.
1
③ 单位矩阵 E 可逆，且 E E .
§4.4 矩阵的逆
3、推论：设A、B为 n 级方阵，若 AB E ,
1 1 A B , B A. 则A、B皆为可逆矩阵，且
证： 从而
AB E
A 0, B 0.
AB A B E 1
由定理知，A、B皆为可逆矩阵. 再由
A1 ( AB) A1 E ,
( AB)B1 EB1 ,
推广
A1 A2 Am A A A .
1
1 m
1 2
1 1
§4.4 矩阵的逆
4 若A可逆, 则A 亦可逆 , 且 A
T
T 1
A .
1 T
1
(5) 若A可逆，则 A 亦 可逆，且 A (6) 若A可逆，则 A 亦 可逆，且 A
k
k
A . A
再由
A11 2, A21 6, A31 4, A12 3, A22 6, A32 5, A13 2, A23 2, A33 2.
* 2 6 4 A 1 有 A 1 3 6 5 . A 2 2 2 2
§4.4 矩阵的逆
2)
A a1a2
an ,
∴当 ai 0 ( i 1,2, 且由于
, n) 时，A可逆.
a1 a2
1 a 1 1 a2 an
1 an
1 1
E 1
1 a1 1 1 a 2 A
0 0 dE . d
同理, A* A dE .
2、定理：矩阵A可逆当且仅当 A 0, （即A
非退化的），且
* A 1 A . A
证：若 A 0, 由 AA* A* A A E A* A* A E 得 A A A * A 1 . 所以，A可逆，且 A A 反过来，若A可逆，则有 AA1 E , 两边取行列式，得 A A1 E 1. A 0.
1
A
1
k
.
注： 当 A 0 时，定义
A E, A
0 k
(A )
1 k
则有
A A A
,
A
A , , Z
§4.4 矩阵的逆
2 A 3 A 10 E 0, 例2 设方阵 A 满足
现在的问题是：在什么条件下矩阵 A 是可逆 的？ 如果 A 可逆，怎样求 A-1 ？ 为此先引入伴随
矩阵的概念.
§4.4 矩阵的逆
二、矩阵可逆的判定及逆矩阵的求法
1、伴随矩阵 定义 设 Aij 是矩阵 A (aij )nn 中元素 aij 的代数
余子式，矩阵
A11 A21 A12 A22 * A A A 1n 2 n
即有， A1 B, B1 A.
§4.4 矩阵的逆
例1 判断矩阵A是否可逆，若可逆，求其逆.
1 2 3 1) A 2 2 1 3 4 3
a1 a2 2) A an
§4.4 矩阵的逆
解：1） ∴ A可逆.
1 2 3 2 2 1 2, 3 4 3
2. 逆矩阵的唯一性
若方阵 A 可逆，则其逆矩阵唯一 .
证明
有 于是
设 B 和 C 都是 A 的逆矩阵，则由定义
AB = BA = E，AC = CA = E，
B = BE = B( AC ) = ( BA )C = EC = C .
所以逆矩阵唯一.
证毕
§4.4 矩阵的逆
三、矩阵可逆的条件
d A.
立即可得,
a11 a12 a21 a22 * AA a a n1 n 2
a1n A11 A21 a2 n A12 A22 ann A1n A2 n
An1 An 2 Ann
§4.4
d 0 0 d 0 0 矩阵的逆
一、引例
引例 1 矩阵与复数
引例 2 坐标旋转变换 复数可以用二维有序数组来表示，如复数 a+bi
可表示为 (a , b) ，因此，从结构上看复数是矩阵的 引例 3 线性变换的逆变换 特殊情形 . 在第二节我们也看到，矩阵与复数相 在平面直角坐标系 xOy 中，将两个坐标轴同 仿，有加法、减法、乘法三种运算 . 我们知道，复 时绕原点旋转 角 ( 逆时针为正，顺时针为负 )， 设给定一个线性变换 数的乘法运算有逆运算，那么矩阵的乘法运算是否 就得到一个新的直角坐标系 (见图 3) ． 平面上 4 a– x , y1 a11 x1 a12 x2 1n n 也有逆运算呢？ 如果有的话，这种运算如何定义， Ｐ 任何一点 a21 x1 a22 x2 a2 n xn , y2 在两个坐标系中的坐标分别记为
称为A的伴随矩阵.
An1 An 2 Ann
性质： AA* A* A A E
§4.4 矩阵的逆
证：由行列式按一行（列）展开公式
ak 1 Ai 1 ak 2 Ai 2 a1l A1 j a2 l A2 j akn Ain d , k i 0, k i anl Anj d , l j 0, l j
. 1 an
§4.4 矩阵的逆
三、逆矩阵的运算规律
1 若A可逆, 则A 亦可逆, 且A
1 1 1
A.
2 若A可逆, 数 0, 则A可逆, 且
A A1 .
1
1
3 若A, B为同阶方阵且均可逆 , 则AB亦可逆, 且
A B 1 B 1 A 1
一、可逆矩阵的概念
定义 设A为n级方阵，如果存在n级方阵B，使得
AB＝BA＝E 则称A为可逆矩阵，称B为A的逆矩阵.
1 A . 注： ① 可逆矩阵A的逆矩阵是唯一的，记作
1 A ② 可逆矩阵A的逆矩阵 也是可逆矩阵，且
A
1
1
A.
1
③ 单位矩阵 E 可逆，且 E E .
§4.4 矩阵的逆
3、推论：设A、B为 n 级方阵，若 AB E ,
1 1 A B , B A. 则A、B皆为可逆矩阵，且
证： 从而
AB E
A 0, B 0.
AB A B E 1
由定理知，A、B皆为可逆矩阵. 再由
A1 ( AB) A1 E ,
( AB)B1 EB1 ,
推广
A1 A2 Am A A A .
1
1 m
1 2
1 1
§4.4 矩阵的逆
4 若A可逆, 则A 亦可逆 , 且 A
T
T 1
A .
1 T
1
(5) 若A可逆，则 A 亦 可逆，且 A (6) 若A可逆，则 A 亦 可逆，且 A
k
k
A . A
再由
A11 2, A21 6, A31 4, A12 3, A22 6, A32 5, A13 2, A23 2, A33 2.
* 2 6 4 A 1 有 A 1 3 6 5 . A 2 2 2 2
§4.4 矩阵的逆
2)
A a1a2
an ,
∴当 ai 0 ( i 1,2, 且由于
, n) 时，A可逆.
a1 a2
1 a 1 1 a2 an
1 an
1 1
E 1
1 a1 1 1 a 2 A
0 0 dE . d
同理, A* A dE .
2、定理：矩阵A可逆当且仅当 A 0, （即A
非退化的），且
* A 1 A . A
证：若 A 0, 由 AA* A* A A E A* A* A E 得 A A A * A 1 . 所以，A可逆，且 A A 反过来，若A可逆，则有 AA1 E , 两边取行列式，得 A A1 E 1. A 0.
1
A
1
k
.
注： 当 A 0 时，定义
A E, A
0 k
(A )
1 k
则有
A A A
,
A
A , , Z
§4.4 矩阵的逆
2 A 3 A 10 E 0, 例2 设方阵 A 满足
现在的问题是：在什么条件下矩阵 A 是可逆 的？ 如果 A 可逆，怎样求 A-1 ？ 为此先引入伴随
矩阵的概念.
§4.4 矩阵的逆
二、矩阵可逆的判定及逆矩阵的求法
1、伴随矩阵 定义 设 Aij 是矩阵 A (aij )nn 中元素 aij 的代数
余子式，矩阵
A11 A21 A12 A22 * A A A 1n 2 n
即有， A1 B, B1 A.
§4.4 矩阵的逆
例1 判断矩阵A是否可逆，若可逆，求其逆.
1 2 3 1) A 2 2 1 3 4 3
a1 a2 2) A an
§4.4 矩阵的逆
解：1） ∴ A可逆.
1 2 3 2 2 1 2, 3 4 3