标准粒子群算法(PSO)及其Matlab程序和常见改进算法
matlab粒子群优化算法

matlab粒子群优化算法Matlab粒子群优化算法(Particle Swarm Optimization,简称PSO)是一种模拟鸟群觅食行为的优化算法,它通过模拟粒子在解空间中搜索最优解的过程,来解决各种优化问题。
本文将介绍PSO 算法的原理和应用,以及如何在Matlab中实现PSO算法。
PSO算法的原理基于群体智能的思想,它模拟了鸟群觅食的行为。
在PSO算法中,解空间被表示为一群粒子,每个粒子代表一个解,其位置和速度决定了粒子在解空间中的搜索行为。
每个粒子通过与当前最优解和全局最优解的比较,来更新自己的速度和位置,从而逐渐靠近最优解。
PSO算法的基本流程如下:1. 初始化粒子群的位置和速度;2. 计算每个粒子的适应度值;3. 更新每个粒子的速度和位置,同时更新当前最优解和全局最优解;4. 判断终止条件是否满足,如果满足则结束,否则返回步骤2。
PSO算法的核心是速度和位置的更新。
速度的更新公式为:v_i(t+1) = w * v_i(t) + c1 * rand() * (pbest_i - x_i(t)) + c2 * rand() * (gbest - x_i(t))其中,v_i(t+1)是粒子i在时间t+1时的速度,w是惯性权重,c1和c2分别是个体和社会学习因子,rand()是一个0-1之间的随机数,pbest_i是粒子i的个体最优解,x_i(t)是粒子i在时间t时的位置,gbest是全局最优解。
位置的更新公式为:x_i(t+1) = x_i(t) + v_i(t+1)PSO算法的优点是简单易用、全局搜索能力强、收敛速度快等。
它广泛应用于函数优化、神经网络训练、机器学习等领域。
在Matlab 中,可以使用内置的pso函数来实现PSO算法。
下面以一个函数优化问题为例,演示如何在Matlab中使用PSO算法。
假设我们要优化的目标函数是f(x) = x^2,其中x的取值范围是[-5, 5]。
粒子群改进算法 matlab

粒子群改进算法matlab-概述说明以及解释1.引言概述部分的内容可如下编写:1.1 概述粒子群算法(Particle Swarm Optimization, PSO)是一种基于群体智能的优化算法,通过模拟鸟群或鱼群等自然界中群体行为的方式,来寻找最优解。
它最初由Russell Eberhart和James Kennedy于1995年提出,并在之后的发展中得到了广泛应用。
PSO算法的核心思想是将待求解问题的可能解看作是群体中的粒子,并通过模拟粒子间的交流和协作来不断优化解空间,在寻找最优解的过程中逐步收敛。
每个粒子通过记忆自己的历史最优解和整个群体中的全局最优解来进行自我调整和更新。
在每一次迭代中,粒子根据自身的记忆和全局信息进行位置的更新,直到达到预设的停止条件。
PSO算法具有简单、易于实现和快速收敛等特点,广泛应用于函数优化、组合优化、机器学习等领域。
然而,传统的PSO算法也存在着较为明显的局限性,如易陷入局部最优解、对参数设置较为敏感等问题。
为了克服传统PSO算法的局限性,研究者们提出了各种改进的方法,从算法思想到参数设置进行了深入研究。
本文旨在介绍粒子群改进算法在Matlab环境下的实现。
首先对传统的粒子群算法进行了详细的介绍,包括其原理、算法步骤、优缺点以及应用领域。
然后,进一步介绍了粒子群改进算法的各种改进方法,其中包括改进方法1、改进方法2、改进方法3和改进方法4等。
最后,通过Matlab环境的配置和实验结果与分析来展示粒子群改进算法在实际应用中的性能和效果。
本文的结论部分总结了主要发现、研究的局限性,并展望了未来的研究方向。
综上所述,本文将全面介绍粒子群改进算法的原理、算法步骤、实现过程和实验结果,旨在为读者提供一个详细的了解和研究该算法的指南。
1.2文章结构1.2 文章结构:本文主要包括以下几个部分的内容:第一部分为引言,介绍了本文的背景和目的,概述了即将介绍的粒子群改进算法的原理和优缺点。
pso算法matlab代码

pso算法matlab代码pso算法是一种优化算法,全称为粒子群优化算法(Particle Swarm Optimization)。
它模拟了鸟群或者鱼群的行为,通过不断地迭代寻找最优解。
在许多优化问题中,pso算法都有着良好的表现,特别是在连续空间的优化问题中。
在matlab中实现pso算法并不复杂,以下是一个简单的例子:```matlabfunction [best_pos, best_val] = pso_algorithm(fitness_func,num_particles, num_iterations, range)% 初始化粒子的位置和速度positions = rand(num_particles, length(range)) .* (range(2) - range(1)) + range(1);velocities = rand(num_particles, length(range)) .* (range(2) - range(1)) + range(1);% 初始化每个粒子的最佳位置和适应度值personal_best_pos = positions;personal_best_val = arrayfun(fitness_func, personal_best_pos);% 初始化全局最佳位置和适应度值[global_best_val, global_best_idx] = min(personal_best_val);global_best_pos = personal_best_pos(global_best_idx, :);% 开始迭代for iter = 1:num_iterations% 更新粒子的速度和位置inertia_weight = 0.9 - iter * (0.5 / num_iterations); % 慢慢减小惯性权重cognitive_weight = 2;social_weight = 2;r1 = rand(num_particles, length(range));r2 = rand(num_particles, length(range));velocities = inertia_weight .* velocities + ...cognitive_weight .* r1 .* (personal_best_pos - positions) + ...social_weight .* r2 .* (global_best_pos - positions);positions = positions + velocities;% 更新每个粒子的最佳位置和适应度值new_vals = arrayfun(fitness_func, positions);update_idx = new_vals < personal_best_val;personal_best_pos(update_idx, :) = positions(update_idx, :);personal_best_val(update_idx) = new_vals(update_idx);% 更新全局最佳位置和适应度值[min_val, min_idx] = min(personal_best_val);if min_val < global_best_valglobal_best_val = min_val;global_best_pos = personal_best_pos(min_idx, :);endendbest_pos = global_best_pos;best_val = global_best_val;end```上面的代码实现了一个简单的pso算法,其中`fitness_func`是待优化的目标函数,`num_particles`是粒子数量,`num_iterations`是迭代次数,`range`是变量的范围。
pso粒子群优化算法matlab程序

clear all; clc; format long; %------给定初始化条件--------------------------------------------- c1=1.4962; %学习因子学习因子 1 c2=1.4962; %学习因子学习因子 2 w=0.7298; %惯性权重惯性权重MaxDT=1000; %最大迭代次数最大迭代次数D=10; %搜索空间维数(未知数个数)搜索空间维数(未知数个数)N=40; %初始化群体个体数目初始化群体个体数目eps=10^(-6); %设置精度(在已知最小值时候用) %------初始化种群的个体(可以在这里限定位置和速度的范围)----------- for i=1:N for j=1:D x(i,j)=randn; %随机初始化位置随机初始化位置v(i,j)=randn; %随机初始化速度随机初始化速度end end %------先计算各个粒子的适应度,并初始化先计算各个粒子的适应度,并初始化 Pi 和Pg--------------------- for i=1:N p(i)=fitness(x(i,:),D); y(i,:)=x(i,:); end pg=x(1,:); %Pg 为全局最优为全局最优for i=2:N if fitness(x(i,:),D)<fitness(pg,D) pg=x(i,:); end end %------进入主要循环,按照公式依次迭代,直到满足精度要求----------- for t=1:MaxDT for i=1:N v(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:)); x(i,:)=x(i,:)+v(i,:); if fitness(x(i,:),D)<p(i) p(i)=fitness(x(i,:),D); y(i,:)=x(i,:); end if p(i)<fitness(pg,D) pg=y(i,:); end end Pbest(t)=fitness(pg,D); end %------最后给出计算结果最后给出计算结果disp('*************************************************************') disp('函数的全局最优位置为:') Solu on=pg' disp('最后得到的优化极值为:') Result=fitness(pg,D) disp('*************************************************************') %------算法结束---DreamSun GL & HF---------------------------------- 适应度函数源程序(fitness.m)func on result=fitness(x,D) sum=0; for i=1:D sum=sum+x(i)^2; end result=sum; 。
粒子群优化算法介绍及matlab程序
粒子群优化算法(1)—粒子群优化算法简介PSO算法就是模拟一群鸟寻找食物的过程,每个鸟就是PSO中的粒子,也就是我们需要求解问题的可能解,这些鸟在寻找食物的过程中,不停改变自己在空中飞行的位置与速度。
大家也可以观察一下,鸟群在寻找食物的过程中,开始鸟群比较分散,逐渐这些鸟就会聚成一群,这个群忽高忽低、忽左忽右,直到最后找到食物。
这个过程我们转化为一个数学问题。
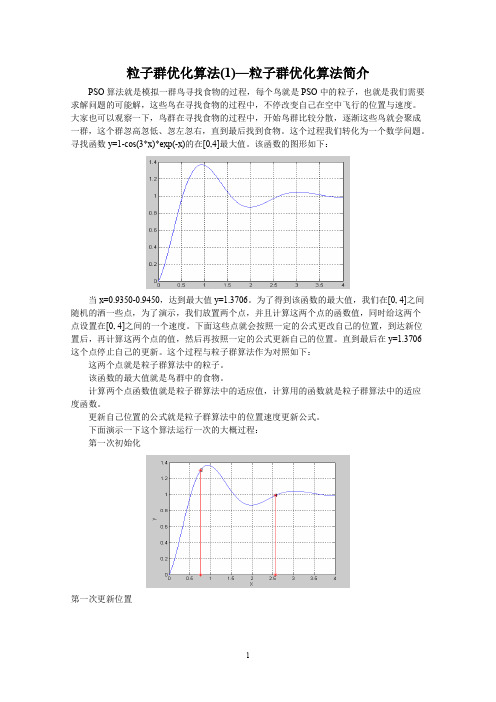
寻找函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
该函数的图形如下:当x=0.9350-0.9450,达到最大值y=1.3706。
为了得到该函数的最大值,我们在[0, 4]之间随机的洒一些点,为了演示,我们放置两个点,并且计算这两个点的函数值,同时给这两个点设置在[0, 4]之间的一个速度。
下面这些点就会按照一定的公式更改自己的位置,到达新位置后,再计算这两个点的值,然后再按照一定的公式更新自己的位置。
直到最后在y=1.3706这个点停止自己的更新。
这个过程与粒子群算法作为对照如下:这两个点就是粒子群算法中的粒子。
该函数的最大值就是鸟群中的食物。
计算两个点函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。
更新自己位置的公式就是粒子群算法中的位置速度更新公式。
下面演示一下这个算法运行一次的大概过程:第一次初始化第一次更新位置第二次更新位置第21次更新最后的结果(30次迭代)最后所有的点都集中在最大值的地方。
粒子群优化算法(2)—标准粒子群优化算法在上一节的叙述中,唯一没有给大家介绍的就是函数的这些随机的点(粒子)是如何运动的,只是说按照一定的公式更新。
这个公式就是粒子群算法中的位置速度更新公式。
下面就介绍这个公式是什么。
在上一节中我们求取函数y=1-cos(3*x)*exp(-x)的在[0, 4]最大值。
并在[0,4]之间放置了两个随机的点,这些点的坐标假设为x1=1.5,x2=2.5;这里的点是一个标量,但是我们经常遇到的问题可能是更一般的情况—x 为一个矢量的情况,比如二维z=2*x1+3*x22的情况。
(完整word版)用MATLAB编写PSO算法及实例

用MATLAB 编写PSO 算法及实例1.1 粒子群算法PSO 从这种模型中得到启示并用于解决优化问题。
PSO 中,每个优化问题的潜在解都是搜索空间中的一只鸟,称之为粒子。
所有的粒子都有一个由被优化的函数决定的适值( fitness value) ,每个粒子还有一个速度决定它们飞翔的方向和距离。
然后粒子们就追随当前的最优粒子在解空间中搜索。
PSO 初始化为一群随机粒子(随机解),然后通过迭代找到最优解。
在每一次迭代中,粒子通过跟踪两个极值来更新自己;第一个就是粒子本身所找到的最优解,这个解称为个体极值;另一个极值是整个种群目前找到的最优解,这个极值是全局极值。
另外也可以不用整个种群而只是用其中一部分作为粒子的邻居,那么在所有邻居中的极值就是局部极值。
假设在一个维的目标搜索空间中,有个粒子组成一个群落,其中第个粒子表示为一个维的向量,。
第个粒子的“飞行 ”速度也是一个维的向量,记为,。
第个粒子迄今为止搜索到的最优位置称为个体极值,记为,。
整个粒子群迄今为止搜索到的最优位置为全局极值,记为在找到这两个最优值时,粒子根据如下的公式(1.1)和( 1.2)来更新自己的速度和位置:(1.1) (1. 2)其中:和为学习因子,也称加速常数(acceleration constant),和为[0,1]范围内的均匀随机数。
式(1.1)右边由三部分组成,第一部分为“惯性(inertia)”或“动量(momentum)”部分,反映了粒子的运动“习惯(habit)”,代表粒子有维持自己D N i D ),,,(21iD i i i x x x X N i ,,2,1 i D ),,21i iD i i v v v V ,( 3,2,1 i i ),,,(21iD i i best p p p p N i ,,2,1 ),,,(21gD g g best p p p g )(2211id gd id id id id x p r c x p r c v w v id id id v x x 1c 2c 1r 2r先前速度的趋势;第二部分为“认知(cognition)”部分,反映了粒子对自身历史经验的记忆(memory)或回忆(remembrance),代表粒子有向自身历史最佳位置逼近的趋势;第三部分为“社会(social)”部分,反映了粒子间协同合作与知识共享的群体历史经验。
pso算法matlab程序

pso算法matlab程序PSO(粒子群优化)算法是一种启发式优化算法,用于解决各种优化问题。
在Matlab中实现PSO算法可以通过以下步骤进行:1. 初始化粒子群:首先,定义需要优化的目标函数,然后确定粒子群的规模、搜索空间的范围、最大迭代次数等参数。
在Matlab中可以使用数组或矩阵来表示粒子群的位置和速度。
2. 计算适应度:根据目标函数,计算每个粒子的适应度值,以便评估其在搜索空间中的位置的好坏程度。
3. 更新粒子的速度和位置:根据PSO算法的公式,更新每个粒子的速度和位置。
这个过程涉及到调整粒子的速度和位置,使其朝着适应度更高的方向移动。
4. 更新全局最优解:在整个粒子群中找到最优的粒子,即具有最佳适应度值的粒子,然后更新全局最优解。
5. 循环迭代:重复步骤3和步骤4,直到满足停止迭代的条件(如达到最大迭代次数或达到精度要求)。
在Matlab中,可以使用循环结构和数组操作来实现上述步骤。
以下是一个简单的PSO算法的Matlab程序示例:matlab.% 定义目标函数。
function z = objective_function(x)。
z = x(1)^2 + x(2)^2; % 以x1和x2为变量的目标函数示例(可根据实际情况修改)。
% 初始化粒子群。
n = 30; % 粒子数量。
max_iter = 100; % 最大迭代次数。
c1 = 2; % 学习因子。
c2 = 2; % 学习因子。
w = 0.7; %惯性权重。
x = rand(n, 2); % 随机初始化粒子的位置。
v = rand(n, 2); % 随机初始化粒子的速度。
pbest = x; % 个体最佳位置。
pbest_val = zeros(n, 1); % 个体最佳适应度值。
gbest = zeros(1, 2); % 全局最佳位置。
gbest_val = inf; % 全局最佳适应度值。
% 迭代优化。
for iter = 1:max_iter.for i = 1:n.% 计算适应度。
Matlab中的粒子群优化算法详解

Matlab中的粒子群优化算法详解引言:粒子群优化算法(Particle Swarm Optimization, PSO)是一种模拟鸟群觅食行为的优化算法,具有简单易实现、无需求导和全局搜索能力强等特点。
该算法在解决多种问题中得到广泛应用,特别是在机器学习、智能优化等领域。
本文将详细介绍Matlab中粒子群优化算法的实现过程及应用。
一、粒子群优化算法原理粒子群优化算法源自于对鸟群觅食行为的模拟。
假设一个鸟群中的每个个体被称为粒子,所有粒子共同组成了一个搜索空间,每个粒子会根据自身的当前位置和历史最佳位置进行搜索,并且受到其邻近粒子的信息影响。
通过不断的迭代运算,粒子们逐渐收敛到全局最优解或局部最优解。
具体算法流程如下:1. 初始化粒子群的位置和速度。
2. 计算每个粒子的适应度值,并更新个体最优位置。
3. 根据全局最优位置调整粒子的速度和位置。
4. 重复执行第2步和第3步,直到满足终止条件。
二、Matlab中粒子群优化算法实现步骤在Matlab中,可以通过以下步骤来实现粒子群优化算法:1. 初始化粒子群的位置和速度。
首先需要确定粒子群的大小,即粒子的个数。
对于每个粒子,需要随机生成一个初始位置和速度。
可以使用Matlab中的rand函数来生成指定范围内的随机数。
问题优劣的指标,因此需要根据具体问题来确定。
对于更新个体最优位置,可以通过比较当前适应度值和历史最佳适应度值的大小,选择适应度更优的位置进行更新。
3. 根据全局最优位置调整粒子的速度和位置。
粒子的速度和位置的更新是通过以下公式实现的:V(i,j) = w * V(i,j) + c1 * rand() * (P(i,j) - X(i,j)) + c2 * rand() * (G(j) - X(i,j))X(i,j) = X(i,j) + V(i,j)其中,V(i,j)表示第i个粒子在第j个维度上的速度,X(i,j)表示第i个粒子在第j个维度上的位置,P(i,j)表示第i个粒子的历史最佳位置,G(j)表示全局最佳位置,w、c1和c2分别表示惯性权重、个体学习因子和社会学习因子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、粒子群算法概述
粒子群优化算法(PSO)是一种进化计算技术(evolutionary computation),1995 年由Eberhart 博士和kennedy 博士提出,源于对鸟群捕食的行为研究。
该算法最初是受到飞鸟集群活动的规律性启发,进而利用群体智能建立的一个简化模型。
粒子群算法在对动物集群活动行为观察基础上,利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得最优解。
PSO中,每个优化问题的解都是搜索空间中的一只鸟。
我们称之为“粒子”。
所有的粒子都有一个由被优化的函数决定的适应值(fitness value),每个粒子还有一个速度决定他们飞翔的方向和距离。
然后粒子们就追随当前的最优粒子在解空间中搜索。
PSO 初始化为一群随机粒子(随机解)。
然后通过迭代找到最优解。
在每一次迭代中,粒子通过跟踪两个”极值”来更新自己。
第一个就是粒子本身所找到的最优解,这个解叫做个体极值pBest。
另一个极值是整个种群目前找到的最优解,这个极值是全局极值gBest。
另外也可以不用整个种群而只是用其中一部分作为粒子的邻居,那么在所有邻居中的极值就是局部极值。
二、算法原理
粒子群算法采用常数学习因子,及惯性权重,粒子根据如下的公式更新自己的速度和位置。
V ki=ωk V i−1i+c1r1(Q bi−Q k−1i)+c2r2(Q bg−Q k−1i)Q ki=Q k−1i+V ki
三、算法步骤
1、随机初始化种群中各微粒的位置和速度;
2、评价个粒子的适应度,将各粒子的位置和适应度储存在各微粒的pbest(Q bi)中,将所有pbest中适应度最优的个体的位置和适应度存储在gbest(Q bg)中。
3、更新粒子的速度和位移。
V ki=ωk V i−1i+c1r1(Q bi−Q k−1i)+c2r2(Q bg−Q k−1i)Q ki=Q k−1i+V ki
4、对每个微粒,与其前一个最优位置比较,如果较好,则将其作为当前的最优位置。
5、比较当前所有的pbest和上一迭代周期的gbest,更新gbest。
6、若满足停止条件(达到要求精度或迭代次数),搜索停止,输出结果,否则,返回2。
四、算法改进
1、带压缩因子的粒子群算法。
主要是限定学习因子,粒子的更新公式变为为:
V ki=ϕ[V i−1i+c1r1(Q bi−Q k−1i)+c2r2(Q bg−Q k−1i)]Q ki=Q k−1i+V ki
其中,ϕ=22−C−C2−4C√,其中C=c1+c2
2、权重改进的粒子群算法。
随着迭代次数的增加,惯性权重从最大变化到最小。
变化的公式是:
ω=ωmax−t∗(ωmax−ωmin)t max
3、自适应权重法。
主要是为了平衡全局搜索和局部搜索能力。
权重的表达式为:
ω=⎧⎩⎨ωmin−(ωmax−ωmin)∗(f−f m in)f avg−f minωmax,f≤f avg,f>f avg
4、随机权重法。
{ω=μ+σ∗N(0,1)μ=μmin+(μmax−μmin)∗rang(0,1)
5、变学习因子的粒子群算法。
(1)、c1=c2=c max−t∗(c max−c min)t max
(2)、{c1=c1,ini+c1,fin−c1,ini t max c2=c2,ini+c2,fin−c2,ini t max
6、二阶粒子群算法。
V ki=ϕ[V i−1i+c1r1(Q bi−2Q ki+Q k−1i)+c2r2(Q bg−2Q ki+Q k−1i)]Q ki=Q k−1i+V ki
五、粒子群算法参数介绍
标准粒子群算法中,有以下几个参数:
1、fitness,待优化的目标函数
2、粒子数目:N
3、学习因子1:c1
4、学习因子2:c2
5、惯性权重:w
6、最大迭代系数:M
7、自变量的个数:D
1、finess 是待优化的目标函数,如何构造函数是用粒子群算法的前提,构造函数的结构直接决定了计算结果的好坏,特别是在多目标优化的问题中。
2、学习因子一般取2,c1决定着其局部搜寻能力,c2决定着其全局搜寻能力。
3、惯性权重大,便于全局搜索,惯性权重小,便于局部搜索。
4、最大迭代系数一般取1000—10000,具体看精度要求。
5、自变量的个数有目标函数决定。
学习因子、惯性权重是改进粒子群算法的关键
更新函数决定了粒子群算法的本质能力。
function[ xm,fv ]= PSO( fitness,N,c1,c2,w,M,D )
% fitness,待优化的目标函数
% 粒子数目:N
% 学习因子1:c1,一般取2
% 学习因子2:c2,一般取2
% 惯性权重:w
% 最大迭代系数:M
% 自变量的个数:D
% 目标函数取最大值是的自变量值:xm
% 目标函数的最小值:fv
format long;
vmax=0.2*2*pi;
vmin=-0.2*2*pi;
xmax=1*pi;
xmin=-1*pi;
for i=1:N
for j=1:D
x(i,j)=randn;
v(i,j)=randn;
end
end
for i=1:N
p(i)=fitness(x(i,:));
y(i,:)=x(i,:);
end
pg=x(N,:);
for i=1:N-1
if fitness(x(i,:)) < fitness(pg)
pg=x(i,:);
end
end
for t=1:M
for i=1:N
v(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:));
x(i,:)=x(i,:)+v(i,:);
if fitness(x(i,:)) < p(i)
p(i)=fitness(x(i,:));
y(i,:)=x(i,:);
end
if p(i) < fitness(pg)
pg=y(i,:);
end
end
end
xm=pg';
fv=fitness(pg);
format short;
end。
