脉冲响应 状态空间方程
《现代控制理论》(刘豹_唐万生)
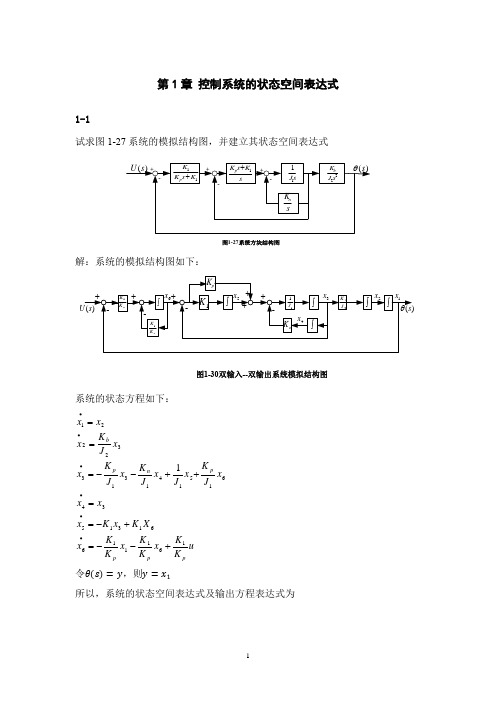
第1章 控制系统的状态空间表达式1-1试求图1-27系统的模拟结构图,并建立其状态空间表达式图1-27系统方块结构图解:系统的模拟结构图如下:图1-30双输入--双输出系统模拟结构图系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===••••••令θ(s)=y ,则y =x 1所以,系统的状态空间表达式及输出方程表达式为[ x 1•x 2•x 3•x 4•x 5•x 6•]=[ 01000000K b J 200000−K p J 1−K n J 11J K p J 100100000−K 100K 1−K 1p−K 1p ][ x 1x 2x 3x4x 5x 6]+[ 00000K 1K p ]uy =[100000][ x 1x 2x 3x 4x 5x 6]1-2有电路如图1-28所示。
以电压u(t)为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻R 2上的电压作为输出量的输出方程。
L1L2U图1-28 电路图解:由图,令i 1=x 1,i 2=x 2,u c =x 3,输出量y =R 2x 2 有电路原理可知:R 1x 1+L 1x 1•+x 3=uL 2x •2+R 2x 2=x 3x 1=x 2+Cx 3•既得 x 1•=−R1L 1x 1−1L 1x 3+1L 1ux •2=−R 2L 2x 2+1L 2x 3 x 3•=−1C x 1+1C x 2y =R 2x 2写成矢量矩阵形式为:[ x 1。
x 2。
x 3。
] =[−R 1L 10−1L 10−R 2L 21L 21C−1C 0][x 1x 2x 3]+[1L 100]u y =[0R 20][x 1x 2x 3] 1-3有机械系统如图1.29所示,M1和M2分别受外力f1和f2的作用.求以M1和M2的运动速度为输出的状态空间表达式.解:以弹簧的伸长度y 1,y 2 质量块M 1, M 2的速率c 1,c 2作为状态变量 即 x 1=y 1,x 2=y 2,x 3=c 1,x 4=c 2根据牛顿定律,对M 1有:M 1dc1dt =f 1-k 1(y 1-y 2)-B 1(c 1-c 2) 对M 2有:M 2dc2dt =f 2+k 1(y 1-y 2)+B 1(c 1-c 2)-k 2y 2-B 2c 2将x 1,x 2,x 3,x 4代入上面两个式子,得 M 1ẋ3=f 1-k 1(x 1-x 2)-B 1(x 3-x 4) M 2ẋ4=f 2+k 1(x 1-x 2)+B 1(x 3-x 4)-k 2x 2-B 2x 4B 1\y 2 c 2 y 1 c 1f 2(t)M 2M 1f 1(t) B 2 K 2K 1整理得 ẋ1=x 3ẋ2=x 4ẋ3=1M 1f 1-k 1M 1x 1+k 1M 1x 2-B 1M 1x 3+B1M 1x 4ẋ4=1M 2f 2+k1M 2x 1-k 1+k 2M 2x 2+B1M 2x 3-B 1+B 2M 2x 4输出状态空间表达式为 y 1=c 1=x 3 y 2=c 2=x 4 1-4两输入u 1,u 2,两输出y 1,y 2的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
第四讲线性动态方程和脉冲响应矩阵

始条件
Ψ i (t0 ) = ei (i=1,2,…,n)
时方程 x = A(t )x 的解。要证明,Ψ1,Ψ2, ,Ψn
是线性无关的n个解。
北京理工大学
线性系统理论 第四章 线性动态方程和脉冲响应矩阵
4.2 线性动态方程的解
状态转移矩阵具有下列重要性质:
(1). Φ (t ,t ) = I
(2). Φ −1 (t ,t0 ) = Ψ (t0 )Ψ −1 (t ) = Φ (t0 ,t ) (3). Φ (t2 ,t0 ) = Φ (t2 ,t1 ) Φ (t1,t0 )
北京理工大学
线性系统理论 第四章 线性动态方程和脉冲响应矩阵
明 确 起 见 , 用 Φ(t;t0,x0,0) 表 示 由 初 始 条 件 x(t0)=x0引起的 x=A(t )x 在时刻t的解。Φ的第四个 自变量表示了u≡0这一事实。x=A(t )x及
x(t0)=x0之解为:
x(t) Φ (t;t0 , x0 , 0) =Φ (t, t0 ) x0
北京理工大学
4.1 引言
本章主要研究动态方程的解,并以状 态转移矩阵来表示动态方程的解。然后提 出等价动态方程的概念并证明一个时不变 动态方程均具有矩阵为常值的等价动态方 程,给出动态方程和脉冲响应矩阵之间的 关系,最后对离散时间线性系统进行了运 动分析。
北京理工大学
线性系统理论 第四章 线性动态方程和脉冲响应矩阵
4.2 线性动态方程的解
根据定义,基本矩阵具有如下性质: Ψ = A (t )Ψ Ψ (t 0 ) = H
其中: H为某个非奇异常量矩阵。
北京理工大学
第二章现代控制理论状态空间表达式
即
(2-11)
(3) 列出状态空间描述iL 1 − ( R + R )C 1 2 R1 L( R1 + R2 ) − R1 1 ( R1 + R2 )C uC ( R1 + R2 )C (2-12) + e(t ) R1 R2 iL R2 − L( R + R ) L( R1 + R2 ) 1 2
§2.1 状态空间描述的概念 2.1.2 控制系统的状态空间描述举例
例2-1 R-L-C系统,求其状态空间描述
R
u
L i
C
uC
解 (1) 确定状态变量 选择电容两端电压 uC (t )、电感通过的电流 i (t ) (2) 列写微分方程并化为一阶微分方程组 基尔霍夫(Kirchhoff)电压定律,
(2-13)
令
1 − ( R + R )C 1 2 A= R1 L( R + R ) 1 2
1 ( R + R )C 2 b= 1 R2 L( R + R ) 1 2
−
R1 ( R1 + R2 )C R1 R2 − L( R1 + R2 )
n 维列向量,状态向量
a12 a1n a22 a2 n an 2 ann
n×n方阵,系统矩阵(或状态矩阵), 反映系统状态的内在联系
§2.1 状态空间描述的概念
状态方程和输出方程

状态方程和输出方程状态方程和输出方程是系统理论中的重要概念,用于描述动态系统的行为。
状态方程描述了系统的状态如何随时间变化,而输出方程则描述了系统的输出如何由状态决定。
在这篇文章中,我们将详细介绍状态方程和输出方程的概念、推导方法和应用。
一、状态方程状态方程又称为状态空间方程或系统方程,用数学表示为:x(t)=A·x(t-1)+B·u(t)其中,x(t)为系统的状态向量,表示系统在其中一时刻的状态;A为状态转移矩阵,描述了系统的状态如何随时间变化;x(t-1)为系统在上一时刻的状态;B为输入矩阵,描述了外部输入信号如何影响系统的状态;u(t)为外部输入信号,表示系统在其中一时刻的输入。
状态方程的物理意义是描述系统的动态行为。
通过状态方程,我们可以了解系统的状态如何由前一时刻的状态和当前的输入决定。
状态方程是描述系统动态行为的基础,可以用于系统的建模、分析和控制。
推导状态方程的方法有两种:物理建模和数学建模。
物理建模是通过系统的物理原理和方程来推导状态方程;数学建模是通过对系统的输入输出进行数学分析,从而推导出状态方程。
物理建模适用于具有物理背景的系统,如机械系统、电路系统等;数学建模适用于所有类型的系统。
二、输出方程输出方程又称为观测方程或测量方程,用数学表示为:y(t)=C·x(t)其中,y(t)为系统的输出向量,表示系统在其中一时刻的输出;C为观测矩阵,描述了系统的输出如何由状态决定;x(t)为系统在其中一时刻的状态。
输出方程的物理意义是描述系统的输出如何由状态决定。
通过输出方程,我们可以了解系统的输出如何与系统的状态相关。
输出方程是描述系统的输出特性的关键,可以帮助我们理解系统的性能和行为。
推导输出方程的方法有直接测量和模型匹配。
直接测量是通过对系统的输出进行实际测量,从而得到输出方程;模型匹配是通过对系统进行数学建模,从而推导出输出方程。
直接测量适用于系统的输出直接可测量的情况;模型匹配适用于系统的输出无法直接测量或想要通过模型进行预测的情况。
脉冲响应函数

脉冲响应函数注意VAR模型过程中的格兰杰检验与变量间的格兰杰检验不是一回事啊!变量间的格兰杰因果是前提是同阶单整Var模型后的格兰杰前提是非同阶单整后差分平稳做VAR模型是非结构化的,且模型形式已被确定为线性形式,需要确定哪些变量间有相互作用及反应变量彼此之间相互影响的最大可能滞后阶数。
因为经济问题中长出现伪回归问题,即经济意义表明几乎没有联系的序列可能出项较大的相关系数。
因此格兰杰检验是做VAR模型必须的。
var的前提是系统稳定(并不一定是各个变量都是稳定的)例如对于3变量的var若有2个水平不平稳有1个水平平稳但是他们3个都是一阶平稳则需要做协整判断用水平的还是用一阶差分的变量进行var若水平的存在协整关系且做单位圆检验系统稳定则可以直接用水平变量做var但是若不存在协整或则系统不稳定则就得用一阶差分变量来做若3个变量都是水平的则直接var就好了用s-plus进行多元VAR-GARCH估计时,是用的MGARCH命令,比如var.bekk=mgarch(It.St.getreturns[,c("interestrate","stockindex")]~ar( 2),~bekk(1,1),armaType="full")。
这时var.bekk的类型是mgarch,即class(var.bekk)="mgarch"。
能不能将模型估计的var部分提取出来,形成一个var对象?这样就可以进行脉冲响应分析了。
请高人指点啊。
建议看一下Nakatani,T.and T.Terasvirta(2009)."Testing for volatilityinteractions in the Constant Conditional Correlation GARCH model."Econometrics Journal 12(1):147-163.Impulse Response Function for Conditional Volatility in GARCH Models Wen-Ling Lin Journal of Business&Economic Statistics,Vol.15,No.1(Jan.,1997),pp.15-25 VAR模型中方程的特征根的倒数要在单位圆内,否则VAR模型不稳定,不能做脉冲响应脉冲响应分析很多时候是根据既定的条件进行的,比如经济意义。
脉冲响应函数

从上式可以看出,g(t)是系统的脉冲响应函数,它等于系统传递函数的拉氏 反变换。g(t)与G(s)有一一对应的关系。g(t)也是线性控制系统的数学模型。
[例2-16]:设系统的脉冲响应函数是
1t
,g求(tG)(s)。4e 2
[解]:
1t
Friday, June 05, 2020
8
1(t)的作用下的输出响应h(t).
0,t 0 x(t) 1(t) 1,t 0 X (s) L[x(t)] L[1(t)] 1
s 1 则输出: y(s) G(s), 单位阶跃响应函数:s h(t) L1[Y (s)] L1[1 G(s)]
s
Friday, June 05, 2020
Friday, June 05, 2020
7
பைடு நூலகம்
基本要求:
会列写控制系统中常用元件的数学模型以及根据系统的组成列写系统的微分方程; 根据微分方程求传递函数的方法; 熟悉绘制结构图和信号流图的方法; 熟悉由结构图和信号流图求取传递函数的方法 -结构图和信号流图的等效变换 -在结构图和信号流图上,用列方程的方法求传递函数 -梅逊公式
5
小结
脉冲响应函数; 脉冲响应函数与传递函数之间的关系; 单位阶跃响应函数; 脉冲响应函数和单位阶跃响应函数之间的关系。
Friday, June 05, 2020
6
本章总结
本章讨论了控制系统数学模型问题,数学模型是实际系统 与控制理论联系的桥梁,建立系统的数学模型是对系统进 行分析的第一步。 本章介绍了时域和频域的数学模型:系统的微分方程,传 递函数,结构图,信号流图,脉冲响应函数等。请注意各 种数学模型之间的联系。 本章研究的数学模型是基于线性定常控制系统的,是研究 输入输出之间的关系,不涉及系统内部状态的变化,故称 为输入输出模型。
2-3 脉冲响应及离散系统

1 x (k ) 0.4 0.3
10 / 13 10 / 13 z 0.8 z 0.5 8 / 13 5 / 13 z 0.8 z 0.5
解
(k ) G k Z
1
{[ zI G]1 z}
10 10 k (0.8) (0.5) k 13 13 8 5 k k (0.8) (0.5) 13 13
u(t ) u(τ )δ(t τ ) d τ
t0
t
(53)
将(53)式代入(28)式
y(t ) C e Ce
A(t t0 ) A( பைடு நூலகம் t0 )
x(t0 ) C e
t0 t t0 t
t
A(t τ )
Bu(τ ) d τ D u(τ )δ(t τ ) d τ
2.5 线性系统的脉冲响应矩阵
0 假设系统初始条件为零, x(t0 ) x(0) 0 输入为单位脉冲函数,即 u(t ) ei δ(t τ ) 0 ei 1 其中,τ为加入单位脉冲的时刻。而 0 ei δ (t τ ) 就表示在 t τ时刻,仅在第i 0 个输入端施加一个单位脉冲。系统的 输出为:
k 0 x(1) Gx(0) k 1 x(2) Gx(1) G 2 x(0) k 2 x(3) Gx(2) G 3 x(0)
k k 1 x(k ) Gx(k 1) G k x(0) (k ) x(0)
其中 系统的输出为
(k ) G k
t0
(56)
(57)
令 t (k 1)T , t0 k0T ,则
x[(k 1)T ] [(k 1)T , k0T ] x(k0T )
现代控制理论--3控制系统的状态方程求解

7
小结:
1.齐次状态方程的解表示了系统在初始条件作用 下的自由运动,又称为零输入解;
2.系统状态的变化实质上是从初始状态开始的状
态转移,而转移规律取决于 eAt ,eA(t-t0) 故称其
为状态转移矩阵.一般用
x
(t) eAt (t t0) eA(tt0)
来表示。 x 0
2 ! 3 !
AA2t1A3t2L 2!
A(I At 1 A2t2 L ) 2!
AeAt eAt A
13
所以当 Φ(t)=eAt时, &(t)A(t) 又因为 Φ(t)=eAt (t=0时) eA0 =I+A0+...=I 所以 Φ(0)=I 故 eAt 是状态转移矩阵Φ(t)
(2)状态转移矩阵Φ(t)是A阵同阶的方阵,其元 素均为时间函数.
sX(s)-x0=AX(s)+BU(s)
即
X(s)=(sI-A)-1[x0+BU(s)]
其中X(s)和U(s)分别为x(t)和u(t)的拉氏变换。
对上式两边取拉氏反变换,并利用卷积分公式,则有
x ( t ) L 1 ( s A ) I 1 x 0 L 1 ( s A ) I 1 B ( s )U
1 0 3x1u
试求:x(0)=0,u(t)=1(t) 时的状态解。
解:1.求 eAt : 由前例得:
eAt
2et 2et
e2t 2e2t
et e2t et 2e2t
25
2. 求x(t)
x(t)eA tx00 teA (t )B u ()d
t2 e (t )e 2 (t ) e (t ) e 2 (t ) 0
由于状态空间表达式由两部分组成,即 x& Ax Bu y Cx Du
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
脉冲响应状态空间方程
脉冲响应是一种常见的信号分析方法,用于描述系统对于单位脉冲输入的响应。
在控制系统和信号处理领域中,脉冲响应经常和状态空间方程一起使用,用于分析和设计系统。
脉冲响应可以看作是系统的加权和,其中加权系数是系统对于单位脉冲输入的响应。
单位脉冲(或者称为单位冲激)是一种理想化的信号,其幅度为1,持续时间极短(可以看作瞬时的),在时间域上表示为一个非常窄的脉冲。
单位脉冲的数学表示为δ(t)。
在连续时间域中,系统的脉冲响应可以通过线性时不变(LTI)系统的冲激响应来描述。
冲激响应(也称为单位冲激响应)是指系统对于单位冲激信号的响应。
对于连续时间域中的脉冲响应h(t),系统的响应可以表示为输入信号与冲激响应的卷积运算。
h(t) = x(t) * δ(t)
其中,*表示卷积运算。
类似地,在离散时间域中,系统的脉冲响应可以通过系统的单位脉冲响应来描述。
单位脉冲响应是指系统对于单位脉冲输入的响应。
对于离散时间域中的脉冲响应h[n],系统的响应可以表示为输入信号与单位脉冲响应的离散卷积运算。
h[n] = x[n] * δ[n]
其中,*表示离散卷积运算。
状态空间方程是一种常用的描述系统动态特性的数学模型。
它是由多个线性微分方程组成的,其中每个方程都描述了系统的一个状态变量的变化率。
状态空间方程通常由状态方程和输出方程组成。
对于线性时不变系统,状态空间方程可以表示为:
x' = Ax + Bu
y = Cx + Du
其中,x是系统的状态向量,表示系统的各个状态变量的值。
x'是状态向量的变化率。
A、B、C和D是系统的系数矩阵,表示系统的结构和特性。
u是系统的输入向量,表示系统的输入信号。
y是系统的输出向量,表示系统的输出信号。
状态空间方程使用线性代数的方法来描述系统,并且具有较好的数学性质。
它可以用于系统分析、控制器设计和系统仿真。
通过状态空间方程,可以计算系统的响应、稳定性、控制输入和输出之间的关系等。
脉冲响应和状态空间方程在信号分析和控制系统设计中经常一起使用。
通过脉冲响应,可以求解系统的频率响应、冲击响应和阶跃响应等。
而状态空间方程可以提供系统的动态特性和控制器设计所需的参数。
两者共同提供了对系统行为的全面认识,有助于分析和设计复杂的系统。
总结来说,脉冲响应和状态空间方程是信号分析和控制系统中常用的数学工具。
脉冲响应用于描述系统对于单位脉冲输入的响应,状态空间方程用于描述系统的动态特性和控制器设计所需的参数。
它们的结合可以提供对系统行为的全面认识,并且在系统分析和设计中起着重要的作用。
