第2章_薄透镜系统的初级像差方程组
合集下载
第2章薄透镜系统的初级像差方程组
南京理工大学紫金学院
像质评价技术
下面由 P ，W 求P，W：
由于实际物平面位在无限远，不需要对物距进行规化，
因此
P ，P W，W只要对
得：P P
(h )3
W W
(h )2
规h,化，由公式
P P (h)32 .2(1 8) 0 3 1 .7 7 1 5 0
4000
h 放大到1，即 h 1
A
u1
h
F
u
A’
F’
f 1
l
f 1
u 1 u
l h
u 1 u
l h
P
P
(h )3
W W
(h )2
南京理工大学紫金学院
像质评价技术
(3) P ，W 对物距的规化
u1 0
f 1
A
u1 h 1
u A’
根据公式 S I I 2 n u K S h z P J W ，并假定入瞳
与透镜重合 hz 0 ，有：
KS
JWWy 2nu 2
由公式 SC lim KS
y0 y
SC K S W 1.1 4 1 4 0 5.7 1 5 0
lF C h 2 C n u 2
(6)
y F C h zh C n u
(7)
南京理工大学紫金学院
像质评价技术
SI 2nu2L hP
(1)
S I I 2 n u K S h z P JW
(2)
S II I n u 2 x ts
W W (h)2 0 .2(8 84 )0 2 1 .1 1 4 4 0 4000
薄透镜教距的测定及像差的观察
x始 10 10 10
x左 21.9 21.8 22.2
d 46.4 46.3 46.0
x右 68.3 68.1 68.2 80 80 80
x末
L 70 70 70
f’ 9.811 9.844 9.943
f’的平均值为 9.866. 【实验结果与分析】 ： 1. 分析本实验的系统误差，对于物距像距法，主要是测量物屏，透镜及像位置时，滑座上的读数准线和被测平 面是否重合，如果不重合将带来误差。对于位移法测凸透镜焦距，不存在这一问题。通过上述两种方法测透镜焦 距符合程度来确定系统误差对结果的影响。 本实验的偶然误差主要是人眼观察，成像清晰度引起的误差，由于人眼对成像的清晰分辨能力有限，所以观察到 的像在一定范围内都清晰，加之其他因素的影响，清晰成像位置会偏离真实像。
广东第二师范学院学生实验报告院系名称物理与信息工程系班别物理与信息工程系班别姓名专业名称学号实验课程名称普通物理实验实验项目名称薄透镜焦距的测定及像差的观察实验时间2016年年4月月30日实验地点物理实验室实验成绩指导老师签名内容包含
广东第二师范学院学生实验报告
院（系）名称 物理与信息工程系 班 姓名 别 专业名称 学号 实验课程名称 普通物理实验 实验项目名称 薄透镜焦距的测定及像差的观察 实验时间 2016 年 4 月 30 日 实验地点 物理实验室 实验成绩 指导老师签名
4
5
由公式（1）与图中的几何关系可得：
1 1 1 u1 D u1 f 1 1 1 u1 d D u1 d f
由上两式右边相等得：
u1
D d
2
将（5）式代入（3）式得：
f
D 2 d 2 D d D d 4D 4D
大学物理 几何光学 薄透镜 (2).ppt
n0 ni 1
i
ff
ni
(nL
1 1)( 1
r1
1) r2
O i
Qp
nL
d 0
d
p1 Q2 Q1 p2
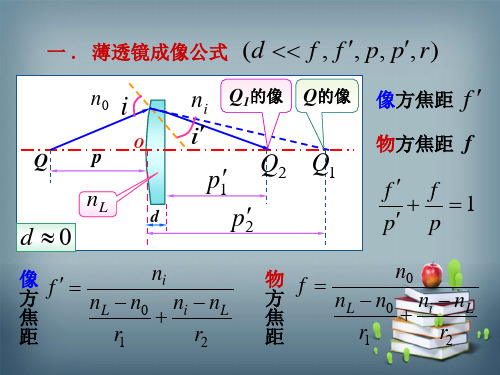
薄透镜成像公式
1 1 1 p p f
➢ 符号规则：以薄透镜光心为分界点，入射光线方向 为正向，如入射光线自左向右，则当物点、像点、焦点 和薄透镜两面的曲率中心在光心右侧时，物距、像距、 焦距和曲率半径均为正；反之，在左侧则为负 .
r1 0, r2 0 r1 r2
r2 r1 0
r1 0, r2 0 r2 0 r1
r1 0,r2 0 r1 r2
➢ 凹、凸透镜成像图
1
1
h0
hi
2
F
p
2
1
h0
2 3
f
F
F
hi 3
p 1 2
➢ 焦平面 过焦点且垂直于主
光轴的平面，平行光线 （近轴）会聚于焦平面.
焦平面
各种形状的透镜 凸透镜（会聚） 凹凸透镜 平凸透镜 双凸透镜 平凸透镜 凹凸透镜
r1 0, r2 0 r1 r2
r1 r2 0
r1 0, r2 0
r1 0 r2
r1 0, r2 0 r1 r2
各种形状的透镜 凹透镜（发散） 凹凸透镜 平凹透镜 双凹透镜 平凹透镜 凹凸透镜
一 . 薄透镜成像公式 (d f , f , p, p, r)
n0 i
O
Qp
nL
d
d 0
ni Q1的像 Q的像
i
p1 Q2 Q1 p2
像方焦距 f
物方焦距 f
f f 1 p p
像 方 焦
工程光学设计 第2章 第二讲
B
垂轴色差 yF C yZF yZC
垂轴色差
A
C
D
y Z C
F yZF yZD
B
垂轴色差
yF C yZF yZC
❖ 3 二级光谱
d(sini sin m ) m
第二章 像差理论
2.3 薄透镜的初级像差理 论
2.3 薄透镜的初级像差理论
一. 薄透镜的初级像差普遍公式
球差和数 S hni(i u)(i i)
四 畸变
无畸变
正畸变
负畸变
负畸变
（a） 光阑位于透镜之前产生负畸变
正畸变
（a） 光阑位于透镜之后产生正畸变
❖ 线畸
yz yz y
q yz 100 %
y
五 色差
1 轴向色差
O1 O2
1 23
兰（F） 绿（D） 红（C）
l
′
F
AF′
AC′
-△l
′
FC
l
′
C
2 垂轴色差
A
F
D
C yZ C yZD yZF
四 反射光学系统和平面光学系统的像 差理论
❖ 1 平面反射镜像差
- i′ -i
-u
u′
2 加工或装配误差产生像差
仪器的主光轴
五 球面反射镜的像差
像点
球心
u=0
-i
- i′ - u′
h
r
光阑在反射镜球心
l
lp
球心
阑
光阑在反射镜顶点
l 球心 ip
lp 阑
六 棱镜或平面平行板的像差
光阑
- i1
正透镜
A
A0′ A′
负透镜
薄透镜的成像公式和放大率
解:
f1 20cm, f 2 5cm, d 16cm
H 2 16cm F1F2 1cm, d H1
f1d 20 16 xH H1 H 320cm 1 f 2d 5 16 x 80cm H H2H 1
拉格朗日—亥姆霍兹恒等式
h1 1 n2h2 2 nk hk k n1h11 n1
例：惠更斯目镜 由两个凸透镜 L1 L2组成，用逐次成像 法求像位置。
已知： f1 3a, f 2 a, d 2a 物点 Q 位于L1前a处 解： - P1= a ，代入第一个透镜的高斯公式
透镜制造者公式（lens-maker，s formula）
ff 1 (nL 1)(1 / r1 1 / r 2)
1 1 1 1 (nL 1)d (nL 1)[ ] f f r1 r 2 nr1r 2 1 1 1 f f 薄透镜的高斯公式： 1 P P f P P
3a 3a 1 得 P a 1
P 1 3 a 1.5a 2
同理对于第二个透镜，有
a a 1 P2 (3 / 2)a 2a
P2 7a / 5 1.4a
例题：凸透镜焦距为10厘米，凹透镜焦距 为4厘米，两个透镜相距12厘米。已知物在凸 透镜左方20厘米处，计算像的位置和横向放大 率并作图。
f1f 2 3a a f HF 3a / 2 (2a)
对于物点 Q ，P =HQ= - 4 a 由高斯公式
f f 1 P P 3a / 2 3a / 2 1 P 4a
得 P H Q 2.4a
即像点位于第二个透镜后1.4 a
第二章_像差
精选可编辑ppt
29
子午平面：轴外物点的主光线与光学系统主轴所构成的平 面，称为光学系统成像的子午面。位于子午面内的那部分 光线，统称为子午光束。子午光束所结成的影像，称为子 午像点(t)。子午像点所在的像平面，称为子午像面。
弧矢像面：过轴外物点的主光线，并与子午面垂直的平面， 称为光学系统成像的弧矢面。位于弧矢面内的那部分光线， 统称为弧矢光束。弧矢光束所结成的影像，称为弧矢像点 (s)。弧矢像点所在的像平面，称为弧矢像面。
辅轴：轴外点和球心的连线称为该折射球面的辅轴
上光线：轴外点发出通过某孔径带上边缘的光线称某孔径
带的上光线
下光线：轴外点发出通过某孔径带下边缘的光线称某孔径
带的下光线
前光线：轴外点发出通过某孔径带前边缘的光线称某孔径
带的前光线
后光线：轴外点发出通过某孔径带后边缘的光线称某孔径
带的后光线
精选可编辑ppt
第二部分：初级像差简介 （Aberration）
精选可编辑ppt
1
高斯光学
光是电磁波
麦克斯韦方程
（原则上） 零波长近似 （实际上）
难以求解
光的所有传播定律 几何光学或光线光学
光线——波面的法线，其方向是在波长趋于零时的光能传播的方向。
几何光学的基础——四大定律
光的直线传播定律 光的独立传播定律 光的反射定律 光的折射定律
薄透镜是最简单的光学系统，它的球差可以写成结构参数的函数即：
当光焦度、物距一定时，也可写成
这里
正透镜恒产生负球差，负透镜 恒产生正球差，当入、出射光 线关于透镜对称时，球差取得 极值（绝对值最小），此时的 透镜形状为最小球差形状。
精选可编辑ppt
24
球差校正方法
第2章_薄透镜系统的初级像差方程组讲解
彗差与光阑位置有关。但球差为零时，彗差即与 光瞳位置无关。
南京理工大学紫金学院
像质评价技术
(3) 像散
SIII nu2 xts
hz2 P 2J h
hz W J 2
h
像散与光阑位置有关，但球差、彗差都为零时，
像散与光瞳位置无关。
(4) 光阑和薄透镜组重合时 hz 0
hz2 W J 2 h2
hz (3 )
h
(5)
SIC nu2lFC h2C
(6)
SIIC nuyFC hzhC
(7)
南京理工大学紫金学院
像质评价技术
像差方程组的用途：
1. 可以得到薄透镜组的像差性质。 2. 已知像差的数值，反求结构参数。
南薄透镜组像差的普遍性质
2.3.1 薄透镜组的单色像差性质 1．一个薄透镜组只能校正 两 种初级单色像差
SI hP hP
SII hz P J W hz P JW
S III
hz2 h
P 2J
hz h
W
J 2
SIV J 2 J 2
SV
hz2 h
P 3J
hz2 W h2
J2
hz (3 )
h
南京理工大学紫金学院
像质评价技术
2．光阑位置对像差的影响
(1) 球差
SI 2nu2L hP
与 h无z 关，所以光阑位置对球差没有影响。
(2) 彗差
SII 2nuKS hz P J W
(7)
南京理工大学紫金学院
像质评价技术
其中的参数：
J nuy nuy
南京理工大学紫金学院
像质评价技术
(3) 像散
SIII nu2 xts
hz2 P 2J h
hz W J 2
h
像散与光阑位置有关，但球差、彗差都为零时，
像散与光瞳位置无关。
(4) 光阑和薄透镜组重合时 hz 0
hz2 W J 2 h2
hz (3 )
h
(5)
SIC nu2lFC h2C
(6)
SIIC nuyFC hzhC
(7)
南京理工大学紫金学院
像质评价技术
像差方程组的用途：
1. 可以得到薄透镜组的像差性质。 2. 已知像差的数值，反求结构参数。
南薄透镜组像差的普遍性质
2.3.1 薄透镜组的单色像差性质 1．一个薄透镜组只能校正 两 种初级单色像差
SI hP hP
SII hz P J W hz P JW
S III
hz2 h
P 2J
hz h
W
J 2
SIV J 2 J 2
SV
hz2 h
P 3J
hz2 W h2
J2
hz (3 )
h
南京理工大学紫金学院
像质评价技术
2．光阑位置对像差的影响
(1) 球差
SI 2nu2L hP
与 h无z 关，所以光阑位置对球差没有影响。
(2) 彗差
SII 2nuKS hz P J W
(7)
南京理工大学紫金学院
像质评价技术
其中的参数：
J nuy nuy
薄透镜系统的初级像差理论
1.6.3薄透镜系统的初级像差理论[2]1.6.3.1初级像差理论在像差理论中，把各项像差和物高y （或视场角ω）、光束孔径h （或孔径角u ）的关系用幂级数的形式表示出来。
把最低次幂对应的像差量称为初级像差，而把较高次幂对应的像差量称为高级像差。
初级像差理论忽略了y 及h 的高次项，在y 及h 均不大的情况下，初级像差理论能够很好的近似代表光学系统的像差性质，为研究和设计工作带来极大的方便。
1.6.3.2薄透镜系统的初级像差方程组如果一个透镜组的厚度和它的焦距比较可以忽略，这样的透镜组称为薄透镜组。
由若干个薄透镜组组成的系统，称为薄透镜系统（透镜组间的间隔是可以任意的）。
对这样的系统在初级像差的范围内，可以建立像差和系统结构参数之间的直接函数关系。
如图1-16为一个简单的薄透镜系统示意图。
我们取两条辅助光线：第一辅助光线是由轴上点发出的经过孔径边缘的光线，它在第i 个透镜上的投射高为i h ；第二辅助光线是轴外点发出的经过孔径中心的光线，它在第i 个透镜上的投射高为zi h 。
而且第i 个透镜的光焦度也是已知的为i ϕ。
每个透镜组的i h 、zi h 和i ϕ叫做透镜组的外部参数，都是已知的，和薄透镜组的具体结构无关；对应的，每个透镜组的i r 、i d 、i n 称为透镜组的内部结构参数。
像差既和外部结构参数有关也和内部结构参数有关。
薄透镜系统初级像差方程组的作用是把系统中各个薄透镜组已知的完部参数和未知的内部结构参数与像差的关系分离开来，便于研究。
下面是各像差和数公式：球差和数''2'2[]i i iS nu L h p δI =-=∑（1-17）弧矢彗差和数'''2[]S zi i i iiS n u K h p J W II =-=-∑∑（1-18）像散和数2''2'2[2]zi zi tsi i i i i ii ih hS n u x p J W Jh h ϕIII =-=-+∑∑∑（1-19）像弯和数 2''2'22[2(1)]z i z iV Pi ii i i i iii h h S n u x p J W J h h ϕμI =-=-++∑∑∑ （1-20）畸变和数 32'''2222[3(3)]ziziziV zi i i i i i i iiih h h S n u y p JW J h h h δϕμ=-=-++∑∑∑ （1-21）轴向色差和数''2'2[]C FC i i iS n u L h C I =-∆=∑（1-22）垂轴色差和数'''[]C FC zi i i iS n u y h hC II =-∆=∑ （1-23）其中，'n 、'u 为系统最后像空间的折射率和孔径角，'''J nu y =是系统的拉格朗日不变量，他们以及每个透镜组的外部参数i h 、zi h 和i ϕ可以当成已知常数，在方括号里的求和式∑中，每个透镜组对应一项。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
南京理工大学紫金学院
像质评价技术
第二章 薄透镜系统的初级像差理论
2.1 概述 2.2 薄透镜系统的初级像差方程组 2.3 薄透镜组像差的普遍性质 2.4 像差特性参数的P，W，C的规化 C 和结构参数的关系 W 2.5 单透镜的 P 、 、 2.6 双胶合透镜组结构参数的求解 2.7 平行玻璃板的初级像差公式 2.8 光学系统消场曲的条件——petzval条件
u
A’
f 1
f 1
l
南京理工大学紫金学院
像质评价技术
（2）保持焦距 f 1 和物距 l 不变，把入射高 h 放大到1，即 h 1
A
u1
h
F F’
u
A’
f 1
f 1
l
1 u u l h 1 u u l h
P
P (h ) 3
W W (h ) 2
南京理工大学紫金学院
像质评价技术
(3) P ， W 对物距的规化
u1 0
A
f 1
h 1
u1
u
F’
A’
l
P P 4u1 (4W 1) u12 (5 2 )
W W u1 (2 )
南京理工大学紫金学院
像质评价技术
(4) C的规化
W 1.67(Q Q0 ) 0.15
P 2.05 2.35(1 1.26) 2 2.21
W 1.67(1 1.26) 0.15 0.284
南京理工大学紫金学院
W 求P，W： 下面由 P ，
像质评价技术
由于实际物平面位在无限远，不需要对物距进行规化，
系统（透镜组之间的间隔可以是任意的）。
南京理工大学紫金学院
像质评价技术
2.2 薄透镜系统的初级像差方程组
B
1
孔径光阑
2
nyA源自uhz1h1
O
h2
hz 2
u
A’
y’
B’
d1
，d1， 2 ， u u， 已知：1 ， h2 第一辅助光线：h1 ， hz 2 第二辅助光线：hz1，
外部参数（与具体结构 参数（r,d,n）无关）
z
(2) (3) (4) (5) (6) (7)
hz2 hz 2 xts P 2 J W J nu 2 h h
xp J 2 2nu 2
hz3 hz2 hz 2 y P 3 J W J ( 3 ) h2 h z h 2 2nu
南京理工大学紫金学院
像质评价技术
2.1 概述
1.初级像差和y、h的关系：
(1) 初级球差
L a1h2
a2 h 2 y KS
3K S KT
(2) 初级彗差
(3) 初级子午场曲(细光束场曲) (4) 初级弧矢场曲
xt a3 y 2
2 x a y s 4
3 y a y z 5
南京理工大学紫金学院
薄透镜系统的初级像差方程组
L
KS
像质评价技术
2 hP 2 n u
对薄透镜组求和
2nu KT 3
(1) (2) (3) (4) (5) (6) (7)
h P J W
z
hz2 hz 2 xts P 2 J W J nu 2 h h
南京理工大学紫金学院
(3) 像散
S III
2 h h z P 2 J z W J 2 nu 2 xts h h
像质评价技术
像散与光阑位置有关，但球差、彗差都为零时， 像散与光瞳位置无关。
(4) 光阑和薄透镜组重合时 hz 0
像散与透镜组的结构无关，无法校正。 (5) 光阑和薄透镜组重合时
南京理工大学紫金学院
像质评价技术
2.4 像差特性参数P，W，C的规化 什么是规化？
任意物距 任意焦距 任意入射高
保持透镜组的几何形状相似
1
1
南京理工大学紫金学院
像质评价技术
A
u1
h F F’
u
A’
f
f
l
南京理工大学紫金学院
像质评价技术
(1) P、W对f’的规化
A
u1
h
F F’
得：
1 0.0156 64.1
实际的C值为：
C 0.0156 C 3.9 106 f 4000
2 2 S n u l h 代入公式 IC C FC
得：
h 2C 802 3.9 106 l FC 62.5 2 2 nu (80 / 4000 )
lFC
h C nu
2
z
2
y FC
h hC nu
南京理工大学紫金学院 其中的参数：
J nuy nu y
像质评价技术
i
i
ni
对单透镜求和
i C i
u i u i P (1 / n ) n i i
hz2 hz 2 x s P 2 J W J (1 ) 2nu 2 h h
hz3 hz2 hz 2 y P 3 J W J ( 3 ) h2 h z h 2 2nu
(5) 初级畸变
(6) 初级轴向色差
C1 （跟材料的色散系数 l FC
有关，与y、h无关）
(7) 初级垂轴色差
y FC C2 y
南京理工大学紫金学院
像质评价技术
2. 薄透镜的概念
如果一个透镜组的厚度和它的焦距比较可以 忽略，这样的透镜组称为薄透镜组。
由若干个薄透镜组构成的系统，称为薄透镜
因此
得： P
， P P
P (h ) 3
W ，只要对 W
规化，由公式 h,
W W (h ) 2
3
80 3 P P (h ) 2.21( ) 1.77 10 5 4000
80 2 W W (h ) 0.284 ( ) 1.14 10 4 4000
hz3 hz2 hz 2 SV 2nuy P 3 J W J h2 h2 h (3 ) z
畸变为零。
南京理工大学紫金学院 (6) 单薄透镜的petzval场曲 xp
S IV 2nu 2 xp J 2
像质评价技术
对单薄透镜组来说，x p 与结构无关。
JW W y 2n u 2 KS 由公式 SC lim y 0 y W 1.14 104 KS SC 5.7 105 y 2 2 KS
南京理工大学紫金学院 下面求色差，由公式
C 1
C 1
像质评价技术
S I hP hP
S II hz P J W hz P JW
S III hz2 hz P 2 J W J 2 h h
S IV J 2 J 2
hz2 hz2 2 hz SV P 3J 2 W J (3 ) h h h
W 1.67(Q Q0 ) 0.15
P P0 0.85(W 0.15) 2
南京理工大学紫金学院
像质评价技术
例：有一平凸透镜，焦距f’＝4000mm，玻璃材料 为K9（n=1.5163, =64.1）用作平行光管物镜， 如下图。通光口径 D ＝ 160mm ，求该透镜的初级 球差、彗差和轴向色差。
南京理工大学紫金学院
2．光阑位置对像差的影响 (1) 球差
S I 2nu 2L hP
像质评价技术
与 hz 无关，所以光阑位置对球差没有影响。
(2) 彗差
hz P J W S II 2nuK S
彗差与光阑位置有关。但球差为零时，彗差即 与光瞳位置无关。
南京理工大学紫金学院
像质评价技术
已知 P W C , 找出玻璃材料和求出结构参数：
南京理工大学紫金学院
像质评价技术
南京理工大学紫金学院
2
南京理工大学紫金学院
根据公式 S I 2nu2L hP ，得：
hP 80 1.77 105 L 1.77 2 2 2nu 2 (80 / 4000 )
像质评价技术
hz P J W ，并假定入瞳 根据公式 S II 2nuK S 与透镜重合 hz 0 ，有：
2
像质评价技术 (1) (2) (3) (4) (5) (6) (7)
S IV 2nu 2 xp J 2
hz3 hz2 hz 2 SV 2nuy P 3 J W J h2 h2 h (3 ) z
h 2C S IC nu 2 l FC
像质评价技术
根据对系统的像差要求，列出初级像差方程组 求解方程组得到系统中每个薄透镜组 的像差特性参数P，W，C 经过规化，求出 P , W , C
求出每个透镜组的结构参数
南京理工大学紫金学院
像质评价技术
2.5 单透镜的 P、W、 C 和结构参数的关系
P P0 2.35(Q Q0 ) 2
D 160
F’
f’＝4000
南京理工大学紫金学院
像质评价技术
Q 由表3－1用插值法得到n=1.5163时的 P 0 ， 0 值为：
P 0 2.05
Q0 1.26
由于透镜为平凸形，并且凸面向前，所以 c2 代入公式 Q c2 1 ，得：
像质评价技术
第二章 薄透镜系统的初级像差理论
2.1 概述 2.2 薄透镜系统的初级像差方程组 2.3 薄透镜组像差的普遍性质 2.4 像差特性参数的P，W，C的规化 C 和结构参数的关系 W 2.5 单透镜的 P 、 、 2.6 双胶合透镜组结构参数的求解 2.7 平行玻璃板的初级像差公式 2.8 光学系统消场曲的条件——petzval条件
u
A’
f 1
f 1
l
南京理工大学紫金学院
像质评价技术
（2）保持焦距 f 1 和物距 l 不变，把入射高 h 放大到1，即 h 1
A
u1
h
F F’
u
A’
f 1
f 1
l
1 u u l h 1 u u l h
P
P (h ) 3
W W (h ) 2
南京理工大学紫金学院
像质评价技术
(3) P ， W 对物距的规化
u1 0
A
f 1
h 1
u1
u
F’
A’
l
P P 4u1 (4W 1) u12 (5 2 )
W W u1 (2 )
南京理工大学紫金学院
像质评价技术
(4) C的规化
W 1.67(Q Q0 ) 0.15
P 2.05 2.35(1 1.26) 2 2.21
W 1.67(1 1.26) 0.15 0.284
南京理工大学紫金学院
W 求P，W： 下面由 P ，
像质评价技术
由于实际物平面位在无限远，不需要对物距进行规化，
系统（透镜组之间的间隔可以是任意的）。
南京理工大学紫金学院
像质评价技术
2.2 薄透镜系统的初级像差方程组
B
1
孔径光阑
2
nyA源自uhz1h1
O
h2
hz 2
u
A’
y’
B’
d1
，d1， 2 ， u u， 已知：1 ， h2 第一辅助光线：h1 ， hz 2 第二辅助光线：hz1，
外部参数（与具体结构 参数（r,d,n）无关）
z
(2) (3) (4) (5) (6) (7)
hz2 hz 2 xts P 2 J W J nu 2 h h
xp J 2 2nu 2
hz3 hz2 hz 2 y P 3 J W J ( 3 ) h2 h z h 2 2nu
南京理工大学紫金学院
像质评价技术
2.1 概述
1.初级像差和y、h的关系：
(1) 初级球差
L a1h2
a2 h 2 y KS
3K S KT
(2) 初级彗差
(3) 初级子午场曲(细光束场曲) (4) 初级弧矢场曲
xt a3 y 2
2 x a y s 4
3 y a y z 5
南京理工大学紫金学院
薄透镜系统的初级像差方程组
L
KS
像质评价技术
2 hP 2 n u
对薄透镜组求和
2nu KT 3
(1) (2) (3) (4) (5) (6) (7)
h P J W
z
hz2 hz 2 xts P 2 J W J nu 2 h h
南京理工大学紫金学院
(3) 像散
S III
2 h h z P 2 J z W J 2 nu 2 xts h h
像质评价技术
像散与光阑位置有关，但球差、彗差都为零时， 像散与光瞳位置无关。
(4) 光阑和薄透镜组重合时 hz 0
像散与透镜组的结构无关，无法校正。 (5) 光阑和薄透镜组重合时
南京理工大学紫金学院
像质评价技术
2.4 像差特性参数P，W，C的规化 什么是规化？
任意物距 任意焦距 任意入射高
保持透镜组的几何形状相似
1
1
南京理工大学紫金学院
像质评价技术
A
u1
h F F’
u
A’
f
f
l
南京理工大学紫金学院
像质评价技术
(1) P、W对f’的规化
A
u1
h
F F’
得：
1 0.0156 64.1
实际的C值为：
C 0.0156 C 3.9 106 f 4000
2 2 S n u l h 代入公式 IC C FC
得：
h 2C 802 3.9 106 l FC 62.5 2 2 nu (80 / 4000 )
lFC
h C nu
2
z
2
y FC
h hC nu
南京理工大学紫金学院 其中的参数：
J nuy nu y
像质评价技术
i
i
ni
对单透镜求和
i C i
u i u i P (1 / n ) n i i
hz2 hz 2 x s P 2 J W J (1 ) 2nu 2 h h
hz3 hz2 hz 2 y P 3 J W J ( 3 ) h2 h z h 2 2nu
(5) 初级畸变
(6) 初级轴向色差
C1 （跟材料的色散系数 l FC
有关，与y、h无关）
(7) 初级垂轴色差
y FC C2 y
南京理工大学紫金学院
像质评价技术
2. 薄透镜的概念
如果一个透镜组的厚度和它的焦距比较可以 忽略，这样的透镜组称为薄透镜组。
由若干个薄透镜组构成的系统，称为薄透镜
因此
得： P
， P P
P (h ) 3
W ，只要对 W
规化，由公式 h,
W W (h ) 2
3
80 3 P P (h ) 2.21( ) 1.77 10 5 4000
80 2 W W (h ) 0.284 ( ) 1.14 10 4 4000
hz3 hz2 hz 2 SV 2nuy P 3 J W J h2 h2 h (3 ) z
畸变为零。
南京理工大学紫金学院 (6) 单薄透镜的petzval场曲 xp
S IV 2nu 2 xp J 2
像质评价技术
对单薄透镜组来说，x p 与结构无关。
JW W y 2n u 2 KS 由公式 SC lim y 0 y W 1.14 104 KS SC 5.7 105 y 2 2 KS
南京理工大学紫金学院 下面求色差，由公式
C 1
C 1
像质评价技术
S I hP hP
S II hz P J W hz P JW
S III hz2 hz P 2 J W J 2 h h
S IV J 2 J 2
hz2 hz2 2 hz SV P 3J 2 W J (3 ) h h h
W 1.67(Q Q0 ) 0.15
P P0 0.85(W 0.15) 2
南京理工大学紫金学院
像质评价技术
例：有一平凸透镜，焦距f’＝4000mm，玻璃材料 为K9（n=1.5163, =64.1）用作平行光管物镜， 如下图。通光口径 D ＝ 160mm ，求该透镜的初级 球差、彗差和轴向色差。
南京理工大学紫金学院
2．光阑位置对像差的影响 (1) 球差
S I 2nu 2L hP
像质评价技术
与 hz 无关，所以光阑位置对球差没有影响。
(2) 彗差
hz P J W S II 2nuK S
彗差与光阑位置有关。但球差为零时，彗差即 与光瞳位置无关。
南京理工大学紫金学院
像质评价技术
已知 P W C , 找出玻璃材料和求出结构参数：
南京理工大学紫金学院
像质评价技术
南京理工大学紫金学院
2
南京理工大学紫金学院
根据公式 S I 2nu2L hP ，得：
hP 80 1.77 105 L 1.77 2 2 2nu 2 (80 / 4000 )
像质评价技术
hz P J W ，并假定入瞳 根据公式 S II 2nuK S 与透镜重合 hz 0 ，有：
2
像质评价技术 (1) (2) (3) (4) (5) (6) (7)
S IV 2nu 2 xp J 2
hz3 hz2 hz 2 SV 2nuy P 3 J W J h2 h2 h (3 ) z
h 2C S IC nu 2 l FC
像质评价技术
根据对系统的像差要求，列出初级像差方程组 求解方程组得到系统中每个薄透镜组 的像差特性参数P，W，C 经过规化，求出 P , W , C
求出每个透镜组的结构参数
南京理工大学紫金学院
像质评价技术
2.5 单透镜的 P、W、 C 和结构参数的关系
P P0 2.35(Q Q0 ) 2
D 160
F’
f’＝4000
南京理工大学紫金学院
像质评价技术
Q 由表3－1用插值法得到n=1.5163时的 P 0 ， 0 值为：
P 0 2.05
Q0 1.26
由于透镜为平凸形，并且凸面向前，所以 c2 代入公式 Q c2 1 ，得：