生产要素的最佳适组合及其计算方法
生产要素的最佳(适)组合及其计算方法

组合方式 a b c d
L(劳动) 1 2 3 6
K(资本) 6 3 2 1
Q(产量) Q0 Q0 Q0 Q0
现有 L 和 K 两种生产要素,有 a 、 b 、 c 、 d 四种组合方式 可以生产出相同的产量Q0 。其等产量线见下图:
1. 等产量线的特征 (1) 等产量线在要素的有效替代范围内是一条向右下方 倾斜的曲线,即存在: K <0。
§4--3 生产要素的最佳(适)组合
在相交点F、G两点的生产要素组合,其购买支出即成本 为C,产量为Q3<Q0; 在切点E点的生产要素组合,其购买支出即成本仍为C, 产量为Q2=Q0。 由于在既定成本C的条件下,得到的产量Q2=Q0>Q3, 所以E点所决定的生产要素组合是最佳要素组合,其组合使 厂商获得利润最大化。 1. 规模经济的确定问题 这里要解决的问题是在不同的成本数量条件下生产要素 组合的投入问题。见下图:
K b K a Lb>La,存在ΔKb<ΔKa,即: < 。 L L
§4--3 生产要素的最佳(适)组合
(3)在同一坐标平面上,可有无数条等产量线且任意两条等产 量线决不会相交。等产量离原点越远表示等产量线代表的 产量越大。见下图:
§4--3 生产要素的最佳(适)组合
生产要素的最佳(适) 组合及其计算方法
生产要素的最佳(适)组合
生产要素的最佳组合目标是利润最大化, 即:在既定的成本条件下,产量(或收益)最大; 或在既定的产量(或收益)条件下,成本最低。 一、生产要素最佳组合原则 所购买的各种生产要素的边际产量与价格的比例相等。即:
MPL MPK PL PK
4.6-4.7最优生产要素组合

F(K,L) (K) L) 2K L F(K,L) 2 (
所以,该企业规模收益不变。
1 2
1 2
1 2
1 2
• (2)企业利润最大时,企业处于均衡状态,满足均衡 MPL 条件
MRTS LK MPK
1
1
r
1 1
所以:
1 1 2 2 2 2 MPL K L ,MPK K L 2 2 MPL K MPK L r
练习题
1、若厂商总成本为24元,由AB 可知L、K的价格为何? 2、生产20单位的产量的最低成 本是多少? 3、其最优要素组合是什么? 4、等成本线由AB平行移到CD, 表明总成本由24元增至多少? 5、如果有效使用32元成本,则 产量应为多少?(大约) 6、在E点上,MRTSLK是多少? 7、是规模递增、递减或不变? 8、这个函数一定是固定比例生 产函数吗? K
1、等斜线——S线
等斜线是一组等产量线中两种要素的边际技术替代
率相等的点的轨迹。
K
C B A
S
Q3 Q2 Q1
L
O
2、扩展线 在生产要素价格、生产技术不变的条件下,当生产成本或者 产量变化时,会形成一系列不同的生产均衡点,这些均衡点的 轨迹就是扩展线。
-----扩展线一定是等斜线。 ----扩展线表示的是企业进行长期生产计划时必须遵循的路线。 K
C3 C2 C1
C
B
N
Q3 Q2 Q1
0
L
练习
• 已知某企业的生产函数为Q=L2/3 K1/3,劳动的价 格W=2,资本的价格r=1,求: (1)当成本C=3000时,企业实现最大产量时的L、 K和Q的均衡值? (2)当产量Q=800时,企业实现最小成本时的L、K 和C的均衡值?
生产要素最优组合

生产要素最优组合生产要素是指用于生产货物和服务的资源,包括劳动力、资本、土地与自然资源等。
对于任何企业来说,选择适当的生产要素的组合是实现最佳生产效果和最大利润的关键。
要素组合是指在一定的资源约束下,将不同的生产要素结合在一起使用,以实现生产目标。
寻找最优的要素组合是一个复杂的经济问题,需要考虑到多种因素,如生产技术、成本、市场需求、资源限制等。
为了寻找最优的要素组合,企业可以运用生产函数和成本函数来分析和决策。
生产函数描述了生产要素与产出之间的关系,它可以帮助企业确定不同要素的边际贡献并做出相应的调整。
成本函数则可以帮助企业评估使用不同要素组合的成本,并选择成本最低的要素组合。
在做出最优要素组合的决策时,企业还需考虑到以下因素:1.产出与要素比例:不同要素的效率和边际贡献不同,在选择要素组合时需要考虑产出与要素的比例。
例如,当劳动力成本较低时,可以多使用劳动力以增加产出;而当资本投入较低时,可以选择增加资本投入以提高效率。
2.要素市场的供求:不同要素的市场供求关系也会影响最优要素组合的选择。
当其中一种要素市场供应充足,价格相对较低时,企业可以选择多使用该要素以降低成本;而当其中一种要素市场供应紧张,价格较高时,企业应考虑调整要素组合以减少成本。
3.产业特性与技术进步:不同产业的特性和技术水平也会影响最优要素组合的选择。
一些产业可能更依赖于劳动力,如服务行业;而一些产业则更依赖于资本和技术,如制造业。
此外,技术的进步也可以改变最优要素组合的选择,例如引入自动化设备可以减少对劳动力的依赖。
4.环境与可持续发展:在选择最优要素组合时,企业还需考虑到环境和可持续发展的因素。
合理利用自然资源、减少环境污染以及提高资源利用效率是企业在决策时应考虑的因素。
总之,寻找最优要素组合是一个复杂的经济问题,需要综合考虑多种因素。
企业可以通过运用生产函数、成本函数和市场供求关系等经济分析工具,并结合实际情况和目标进行合理的决策。
全要素生产率的测算方法及公式

全要素生产率的测算方法及公式全要素生产率(Total Factor Productivity,TFP)是衡量一个经济体在使用全部生产要素(劳动力、资本、技术等)进行生产时,所获得的产出与投入之间的效率关系。
它是指对全部生产要素的综合利用程度,衡量经济体在总体上对资源的综合利用效果。
计算全要素生产率需要考虑到产出、劳动和资本这三个要素,同时,由于技术进步对生产过程的影响,也需要考虑技术因素。
以下是TFP的几种常见的计算方法及公式:1. 准则式法(Index number method)准则式法是衡量不同时期间生产要素的变动程度,通过比较各个时期生产要素的投入与产出的变化来计算TFP。
这种方法的公式可以表示为:TFP=(产出指数)/(劳动力指数x资本指数x技术进步指数)2. 产出剩余法(Output residual method)产出剩余法是通过分析产出与生产要素之间的关系,计算未能通过投入生产要素解释的产出增长率,来衡量技术进步对产出的贡献。
这种方法的公式可以表示为:TFP=ΔY-αΔK-βΔL其中,TFP代表全要素生产率的增长率;ΔY代表产出的增长率;ΔK 代表资本投入的增长率;ΔL代表劳动投入的增长率;α与β分别是资本和劳动的产出弹性系数。
3. 混合生产函数法(Cobb-Douglas production function)混合生产函数法是基于Cobb-Douglas生产函数的框架,通过分析产出、劳动和资本之间的关系,来计算TFP。
这种方法的公式可以表示为:Y=A*f(L,K)其中,Y代表产出;L代表劳动力;K代表资本;A代表技术进步。
4. 修正的Cobb-Douglas生产函数法(Malmquist指数)修正的Cobb-Douglas生产函数法通过计算不同时间点两个生产函数之间的距离,来衡量技术进步对TFP的影响。
这种方法的公式可以表示为:Malmquist指数 = 距离指数 x 效率指数其中,距离指数代表两个生产函数之间的技术进步指数;效率指数代表同一时间点内的生产效率。
两种可变生产要素的最适组合刘艳霞讲解

两种可变生产要素的最适组合刘艳霞讲解【最新版】目录一、引言二、什么是可变生产要素三、最适组合的概念和影响因素四、如何实现最适组合五、结论正文【引言】在经济学中,生产要素是指用于生产商品或服务的资源。
其中,可变生产要素是指在短期内可以调整数量的生产要素,如劳动力和资本。
本文将探讨如何找到这两种可变生产要素的最适组合,以实现最大化的生产效益。
【什么是可变生产要素】可变生产要素主要包括劳动力和资本。
劳动力是指工人的数量和技能水平,资本则包括生产设备、原材料等。
这两种要素在生产过程中是可变的,也就是说,在短期内,我们可以调整它们的数量来满足生产需求。
【最适组合的概念和影响因素】最适组合是指在一定的生产条件下,劳动力和资本的组合可以使得生产效益最大化。
这个组合取决于多种因素,如劳动力和资本的相对价格、生产技术、市场需求等。
在生产过程中,我们需要通过调整劳动力和资本的投入,来找到这个最适组合。
【如何实现最适组合】要实现最适组合,我们需要关注以下几个方面:1.合理配置劳动力:根据生产需要和劳动力的供给情况,合理调整劳动力的投入。
在短期内,我们可以通过加班、招聘等方式来调整劳动力的投入。
2.优化资本结构:合理配置生产设备、原材料等资本,以提高生产效率。
这需要我们关注资本的价格、使用寿命等因素,以实现资本的最优使用。
3.提高生产技术:生产技术的提高可以降低生产要素的投入,从而实现生产效益的提高。
我们需要关注新技术的研发和应用,以提高生产效率。
4.关注市场需求:根据市场需求来调整生产,以实现生产的最大化。
我们需要关注市场的变化,及时调整生产策略。
【结论】通过合理配置劳动力和资本,提高生产技术,关注市场需求,我们可以找到两种可变生产要素的最适组合,从而实现生产效益的最大化。
(完整版)生产要素最优组合
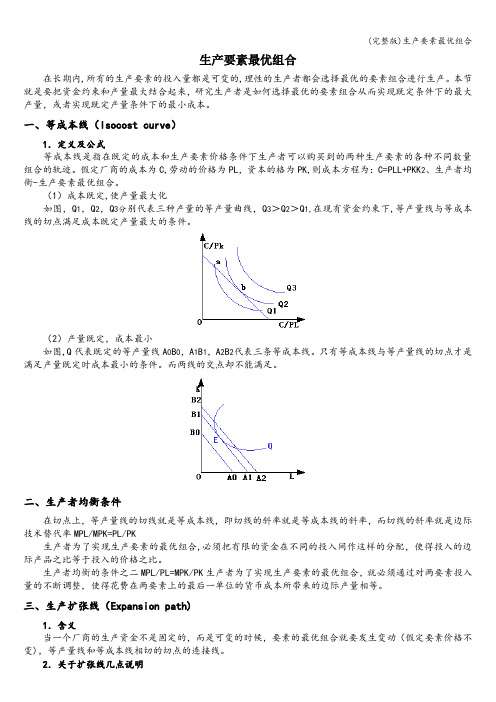
生产要素最优组合在长期内,所有的生产要素的投入量都是可变的,理性的生产者都会选择最优的要素组合进行生产。
本节就是要把资金约束和产量最大结合起来,研究生产者是如何选择最优的要素组合从而实现既定条件下的最大产量,或者实现既定产量条件下的最小成本。
一、等成本线(Isocost curve)1.定义及公式等成本线是指在既定的成本和生产要素价格条件下生产者可以购买到的两种生产要素的各种不同数量组合的轨迹。
假定厂商的成本为C,劳动的价格为PL,资本的格为PK,则成本方程为:C=PLL+PKK2、生产者均衡-生产要素最优组合。
(1)成本既定,使产量最大化如图,Q1,Q2,Q3分别代表三种产量的等产量曲线,Q3>Q2>Q1,在现有资金约束下,等产量线与等成本线的切点满足成本既定产量最大的条件。
(2)产量既定,成本最小如图,Q代表既定的等产量线A0B0,A1B1,A2B2代表三条等成本线。
只有等成本线与等产量线的切点才是满足产量既定时成本最小的条件。
而两线的交点却不能满足。
二、生产者均衡条件在切点上,等产量线的切线就是等成本线,即切线的斜率就是等成本线的斜率,而切线的斜率就是边际技术替代率MPL/MPK=PL/PK生产者为了实现生产要素的最优组合,必须把有限的资金在不同的投入间作这样的分配,使得投入的边际产品之比等于投入的价格之比。
生产者均衡的条件之二MPL/PL=MPK/PK生产者为了实现生产要素的最优组合,就必须通过对两要素投入量的不断调整,使得花费在两要素上的最后一单位的货币成本所带来的边际产量相等。
三、生产扩张线(Expansion path)1.含义当一个厂商的生产资金不是固定的,而是可变的时候,要素的最优组合就要发生变动(假定要素价格不变),等产量线和等成本线相切的切点的连接线。
2.关于扩张线几点说明(1)扩张线是最优要素组合的轨迹,或者说是资金约束下的最大产量或最小成本的轨迹。
(2)扩张线可以描述短期生产行为和长期生产行为。
生产要素最优组合条件

生产要素最优组合条件最优组合是指企业面临资源有限的条件, 选择有效的投资组合,以最大限度地提高经济效益的组织活动称为最佳组合。
一、最优组合要素包括:1、生产要素的分配。
在生产要素的有效分配中,应考虑到最佳投入组合,最佳价格和最佳数量,以确保投资的最高效益。
2、资源的运用。
基本资源的运作,应综合考虑工业因素、限制性文件和社会资源,以优化资源利用效率,实现资源最佳分配和经济效益.3、技术研究与开发。
企业研发的目的是实现有效的开发和创新,以及有效控制生产成本,进而提高企业的竞争力.4、生产计划及管理策略。
企业面临资源有限的条件,要有充分的计划及合理的管理,以确保最佳投资组合.1、合理配置资源。
企业资源包括生产要素和技术、设备、土地、财力和人力等要素,要利用测度技术,合理配置有限的资源,最大程度提高产业经济效益.2、科学变通企业管理。
科学的企业管理是企业走向发展的重要保证,从培训、组织及经营管理三个方面实行科学变通,以确保有效控制企业生产活动,进而提高经济效益.3、突出关键环节和细节处理。
在企业组织管理中,要突出关键环节,把握最核心问题,同时要注重细节,全面深入地实施管理,以确保有效实施企业组织各项行动.4、竞争性投入优化组合。
要根据企业和产业的发展布局,针对当前的实际情况进行经济模型的可行性分析,优化企业的投资组合,避免企业扩张无序,实现最佳投资分配.最佳生产要素组合,必须建立在合理的资源配置、科学的企业管理、突出关键环节和细节处理以及竞争性投入组合优化等原则之上,以达到经济效益最大化的目的。
只有落实这些原则,才能确保最佳组合实施的有效性,从而达到企业发展的最大效益。
长期生产函数之两种生产要素的最适组合

长期生产函数之两种生产要素的最适组合引言在经济学中,生产函数是用来描述一个企业、行业或整个经济体生产的输出与生产要素之间的关系的数学表达式。
长期生产函数则是在长期内稳定的条件下,描述生产要素的最佳组合对产出的影响。
在本文中,我们将讨论长期生产函数中的两种生产要素的最适组合问题。
这两种生产要素可以是任意组合,但在实际应用中,最常见的是劳动力和资本这两种要素。
我们将探讨如何确定这两种生产要素的最佳比例,以实现最大化的产出。
理论背景长期生产函数将输出(产出)表示为劳动力(L)和资本(K)两个生产要素的函数。
通常用数学形式表示如下:Y = F(L,K)其中,Y表示产出(输出),F表示生产函数,L表示劳动力,K表示资本。
因此,我们的目标是找到最佳的L和K的组合,以最大化产出Y。
为了简化讨论,我们假设生产函数具有某些特定的性质,如递增的边际产出、递减的边际产入和规模报酬递增等。
这些假设使得我们可以通过微积分方法来解决最优化问题。
最适组合的确定约束条件在确定最优的L和K的组合之前,我们首先需要确定一些约束条件。
这些约束条件可能是资源的限制、技术的限制、市场条件等。
根据不同的情况,我们可以设定不同的约束条件。
以资源限制为例,我们可以设定总成本不超过某个固定的金额,即:C = wL + rK其中,C表示成本,w表示单位劳动力的工资,r表示单位资本的租金。
在这个约束条件下,我们需要找到L和K的组合,以最大化产出Y。
最优化问题现在,我们可以将长期生产函数的最适组合问题转化为一个最优化问题。
我们的目标是找到最大化产出的L和K的组合,满足成本约束条件。
为了求解最优化问题,可以使用一些常见的最优化算法,如拉格朗日乘子法、等式约束法等。
这些方法可以帮助我们找到最佳的L和K的组合。
实际应用长期生产函数的最适组合问题在实际的经济环境中具有重要的应用价值。
通过确定最佳的L和K的组合,企业可以实现资源的最优利用,从而提高生产效率和竞争力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PLLn + PKKn < C
PLLh + PKKh = C
4. 生产要素最佳组合的图形说明
等产量线与等成本线位于在一个坐标系中,存在三种位 置关系:相切、相离和相交,见下图:
§4-产要素组合,其购买支出即成本 为C,产量为Q3<Q0;
在切点E点的生产要素组合,其购买支出即成本仍为C, 产量为Q2=Q0。
TP=f(L,K)
TP=Q0 为常数
二、等产量线与生产要素最适组合的确定
1.等产量线
等产量线定义:表示某一固定数量的产量(既定产量)可 以用所需的各种生产要素的不同数量的组合生产出来,由这 种不同数量的最大组合所确定的曲线即为等产量线。
等产量线图形表示
见下表:
组合方式 a b c d
L(劳动) 1 2 3 6
——利润最大化条件
式中: MLPT(PL L,K) 劳动L的边际产量;
T(PL,K) MKP K
资本K的边际产量。
1. 满足“在既定的成本条件下,产量(或收益)最大”的 利润最大化的生产要素最佳组合的约束条件:
PLL+PKK=C
2.满足“在既定的产量(或收益)条件下,成本最低”的
利润最大化的生产要素最佳组合的约束条件:
生产要素的最佳(适) 组合及其计算方法
生产要素的最佳(适)组合
生产要素的最佳组合目标是利润最大化, 即:在既定的成本条件下,产量(或收益)最大;
或在既定的产量(或收益)条件下,成本最低。
一、生产要素最佳组合原则 所购买的各种生产要素的边际产量与价格的比例相等。即:
MPL MPK
PL
PK
由于在既定成本C的条件下,得到的产量Q2=Q0>Q3, 所以E点所决定的生产要素组合是最佳要素组合,其组合使 厂商获得利润最大化。
1. 规模经济的确定问题
这里要解决的问题是在不同的成本数量条件下生产要素
组合的投入问题。见下图:
§4--3 生产要素的最佳(适)组合
实现扩大生产规模(Q3→Q2→Q1)的生产要素的最佳 组合是沿着C线的组合,即:(L3,K3)、(L2,K2)、 (L1,K1)。
K(资本) 6 3 2 1
Q(产量) Q0 Q0 Q0 Q0
现有L和K两种生产要素,有a、b、c、d四种组合方式 可以生产出相同的产量Q0 。其等产量线见下图:
1. 等产量线的特征
(1) 等产量线在要素的有效替代范围内是一条向右下方
倾斜的曲线,即存在: K
<0。
L
有效替代范围是指在产量既定的条件下,某一生产要素
§4--3 生产要素的最佳(适)组合
3. 等成本线
表示在PL、PK已知的条件下,用既定的成本C可以购买 各种生产要素数量的最大组合所决定的曲线。
即: PLL + PKK = C
式中C为常数
由上式决定的图形如下:
§4--3 生产要素的最佳(适)组合
图中三种购买组合M、N、H存在:
PLLm + PKKm > C
L
术替代率是递减的。边际技术替代率递减规律是指随着生产 要素L投入量的增加,每增加一单位L所减少的生产要素K的 数量是下降的。
见下图:
Lb>La,存在ΔKb<ΔKa,即:
Kb < L
K a L
。
§4--3 生产要素的最佳(适)组合
(3)在同一坐标平面上,可有无数条等产量线且任意两条等产 量线决不会相交。等产量离原点越远表示等产量线代表的 产量越大。见下图:
的增加,可使另一生产要素减少的范围。有效替代范围常用
脊线规定其范围,见下图:
脊线范围以外, K >0,表明在产量既定的条件下,增加
L
某一生产要素的投入,也必须增加另一生产要素的投入,方 能维持原有的产量Q0,替代是不可能的。
(1) 等产量线是上凹的,说明生产要素之间的替代递减 的。
令MRTS = K ,MRTS称为边际技术替代率,即边际技
