连续时间系统状态方程的离散化
现代控制理论知识点汇总

现代控制理论知识点汇总Revised at 2 pm on December 25, 2020.第一章 控制系统的状态空间表达式1. 状态空间表达式 n 阶DuCx y Bu Ax x+=+= 1:⨯r u 1:⨯m y n n A ⨯: r n B ⨯: n m C ⨯:r m D ⨯:A 称为系统矩阵,描述系统内部状态之间的联系;B为输入(或控制)矩阵,表示输入对每个状态变量的作用情况;C 输出矩阵,表示输出与每个状态变量间的组成关系,D直接传递矩阵,表示输入对输出的直接传递关系。
2. 状态空间描述的特点①考虑了“输入-状态-输出”这一过程,它揭示了问题的本质,即输入引起了状态的变化,而状态决定了输出。
②状态方程和输出方程都是运动方程。
③状态变量个数等于系统包含的独立贮能元件的个数,n 阶系统有n 个状态变量可以选择。
④状态变量的选择不唯一。
⑤从便于控制系统的构成来说,把状态变量选为可测量或可观察的量更为合适。
⑥建立状态空间描述的步骤:a 选择状态变量;b 列写微分方程并化为状态变量的一阶微分方程组;c 将一阶微分方程组化为向量矩阵形式,即为状态空间描述。
⑦状态空间分析法是时域内的一种矩阵运算方法,特别适合于用计算机计算。
3. 模拟结构图(积分器 加法器 比例器)已知状态空间描述,绘制模拟结构图的步骤:积分器的数目应等于状态变量数,将他们画在适当的位置,每个积分器的输出表示相应的某个状态变量,然后根据状态空间表达式画出相应的加法器和比例器,最后用箭头将这些元件连接起来。
4. 状态空间表达式的建立① 由系统框图建立状态空间表达式:a 将各个环节(放大、积分、惯性等)变成相应的模拟结构图;b 每个积分器的输出选作i x ,输入则为i x;c 由模拟图写出状态方程和输出方程。
② 由系统的机理出发建立状态空间表达式:如电路系统。
通常选电容上的电压和电感上的电流作为状态变量。
利用KVL 和KCL 列微分方程,整理。
离散化的状态方程
T ∫0
I ⋅ B ⋅ dt = BT
结论:上式为近似计算方法 例2.6 已知时变系统
0 5(1 − e −5t ) 5 5e −5t u ɺ x= x + −5t −5t 0 5(e − 1) 0 5(1 − e )
试将它离散化,并求出输入和初始条件分别为
0, x(0) = 0时,方程在采样时刻的近似解 u (t ) = 0 1
1 (3)H(T) = ∫ 0 0
T T 1/ 2(1−e )0 1 dt= ∫0 −2t e 1 0 −2t −2t
x 1 [( k + 1)T] x 1 (kT ) (4) = [G (T)] x (kT ) + [H (kT) U (kT)] x 2 [( k + 1)T] 2
归纳:将连续状态方程离散化步骤
1、求Φ(t )=e = L [ SI − A] 2、G(T ) = Φ(T ) = Φ(t ) t = T T At 3、求H (T ) = ∫0 e Bdt 4、求x[(k + 1)T ] = G(T ) x(kT ) + H (T )u (kT )
At
−1
−1
例2.5已知控制对象满足 1 x + 0u,求其离散化方程 ɺ = 0 x 0 1 −2
系统离散状态方程(T=0.1) 可见T较小时, x1[(k + 1)T ] 0.9 0.1 x1(kT ) 0 = + r (kT ) 两种方法得 x2[(k + 1)T ] − 0.1 0.9 x2 (kT ) 0.1 状态空间表 x1(kT ) 达式近似相 输出y(kT ) = [1 0] 等。 x2 (kT ) 离散方程求解可按2.3递推法或Z变换求解
状态方程 离散化 前向欧拉法

状态方程、离散化与前向欧拉法1. 状态方程状态方程是描述动态系统行为的数学模型,可以用来描述物理、生物、经济等各种系统。
在控制论、系统论和动力学中,状态方程常常以微分方程的形式出现,用来描述系统的状态随时间的变化规律。
一般而言,状态方程可以表示为:dx/dt = f(x, u)其中,x表示系统的状态向量,u表示系统的输入向量,f(x, u)表示状态向量x和输入向量u的函数关系。
这个方程可以理解为状态向量x在时间上的导数等于状态向量和输入向量的函数关系。
2. 离散化离散化是将连续时间的系统转换为离散时间的系统的过程。
在实际控制系统中,往往需要将连续时间的状态方程转换为离散时间的状态方程,以便于数字计算机进行处理和控制。
离散化的过程可以通过采样和量化来实现。
采样是指在固定的时间间隔内对系统的状态进行测量,量化是指将连续的状态值映射为离散的数值。
离散化后的状态方程可以表示为:x(k+1) = F(x(k), u(k))其中,k表示离散时间步数,x(k)表示第k个时间步的状态向量,u(k)表示第k个时间步的输入向量,F(x(k), u(k))表示离散时间步之间状态向量和输入向量的函数关系。
3. 前向欧拉法前向欧拉法是一种常用的离散化方法,通过使用离散时间步的导数来近似连续时间的导数。
它的基本思想是将连续时间的状态方程在每个时间步上进行线性化,然后通过计算斜率来估计下一个时间步的状态。
前向欧拉法的离散化过程可以表示为:x(k+1) = x(k) + h * f(x(k), u(k))其中,h表示离散时间步长,f(x(k), u(k))表示在第k个时间步上的状态向量和输入向量的导数。
前向欧拉法的优点是简单易实现,计算量小。
然而,它的精度相对较低,容易积累误差,并且在处理非线性系统时可能出现不稳定的情况。
4. 总结状态方程是描述动态系统行为的数学模型,离散化是将连续时间的系统转换为离散时间的系统的过程,而前向欧拉法是一种常用的离散化方法。
2.3线性连续时间状态空间表达式的离散化

§2.3 线性连续时间状态空间表达式的离散化如果用数字计算机对连续时间状态方程求解,或者对连续受控对象采用数字计算机进行在线控制,都要碰到一个将连续时间系统化为离散时间系统的问题。
本节将讨论线性连续时间状态空间表达式的离散化方法。
一、线性时变系统的离散化 设原线性系统的状态空间表达式为:).()t (u )t (D )t (X )t (C Y )t (u )t (B )t (X )t (A X612⎩⎨⎧+=+=离散化后状态空间表达式为:[]).()kT (u )kT (D )kT (X )kT (C )kT (Y )kT (u )kT (H )kT (X )kT (G T )k (X 6221⎩⎨⎧⋅+⋅=+=+式(2.61)、(2.62)之间的系数关系如下[][]).()t (D )kT (D )t (C )kT (C d )(B ,T )k ()kT (H kT ,T )k ()kT (G kTt kT t T)k (kT632111==+==+=+=⎰τττφφ式中[]kT ,T )k (1+φ表示)t ,t (0φ在kT t T )k (≤≤+1区段内的状态转移矩阵,而)t ,t (0φ则表示原连续系统(2.61)式的状态转移矩阵。
证明:由上节(2.60)式可知(2.61)式的解为:).(d )(u )(B ),t (X )t ,t ()t (X t t 642000ττττφφ⎰+=对上式离散化,令hT t ,T )k (t =+=01,T 为采样周期,则得[][][]).(d )(u )(B ,T )k (X hT ,T )k (T )k (X T )k (hT65211110ττττφφ+++=+⎰+再以hT t ,kT t ==0代入(2.64)式,则得 ).(d )(u )(B ),kT (X )hT ,kT ()kT (X kT hT 6620ττττφφ⎰+=将(2.66)式两边同左乘[]kT ,T )k (1+φ,得[][][][][]).(d )(u )(B ,T )k (X hT ,T )k (d )(u )(B ),kT (kT ,T )k (X )hT ,kT (kT ,T )k ()kT (X kT ,T )k (kT hT kT hT 6721111100ττττφφττττφφφφφ+++=++⋅+=+⎰⎰将(2.65)式减去(2.67)式得:[][][]).(d )(u )(B ,T )k ()kT (X kT ,T )k (T )k (X T )k (kT 6821111ττττφφ+++=+⎰+上式中,令[][]τττφφd )(B ,T )k ()kT (H kT ,T )k ()kT (G T)k (kT⎰+=+=+111设在区间[]T )k (,kT 1+内,)kT (u )(u =τ,则(2.68)式可简写成: [])kT (u )kT (H )kT (X )kT (G T )k (X ⋅+⋅=+1 同时,对(2.61)式输出方程离散化,则证明了)kT (u )kT (D )kT (X )kT (C )kT (Y ⋅+=二、线性时不变系统的离散化 对于线性时不变系统).(uD X C Y u B X A X692⎩⎨⎧+=+=离散化状态空间表达式为).()kT (u D )kT (X C )kT (Y )kT (u )T (H )kT (X )T (G T )k (X 7021⎩⎨⎧+=+=+其中D ,C ),T (H ),T (G 均为常数阵,且).(B)d e ()T (H e)T (G A T AT 7120⎪⎩⎪⎨⎧==⎰ττ证明:由于时不变系统是时变系统的一种特殊情况,所以只需要证明式(2.71)成立即可。
控制系统仿真及MATLAB语言-连续系统的离散化方法

第四章 连续系统的离散化方法
2021/4/10
1
ba12
a2
a2
1 12
a2b1 1 2
三个方程,四个未知数,解不唯一
2各021/个4/10系数的几种取法——见书上。
12
3) r=4时,四阶龙格库塔公式-最常用:
h
xk 1
xk
( 6
K1
2K2
2K3
K4
)
K1 f tk ,xk
K2
K3
f f
tk
tk
h 2
,
xk
h 2 , xk
2 病态系统中绝对值最小的特征值对应于系统动态性能 解中瞬态分量衰减最慢的部分,它决定了整个系统的动 态过渡过程时间的长短。一般与系统中具有最小时间常 数Tmax的环节有关,要求计算步长h取得很大。
3 对于病态问题的仿真需要寻求更加合理的算法,以解 决病态系统带来的选取计算步长与计算精度,计算时间 之间的矛盾。
在仿真中,对于n阶系统,状态方程可以写成一阶微分方程
xi ai1x1 ai2 x2 ain xn biu fi (t, x1, x2, x3, , xn )(i 1, 2, , n)
2021/4/10
14
根据四阶龙格-库塔公式,有
T=tk+h时刻的xi值
T=tk时刻的xi值
xk 1 i
2021/4/10 K3 [k13
连续系统的状态变量方程求解

连续系统的状态变量方程求解连续系统的状态变量方程求解通常采用数值方法,例如龙格-库塔法(Runge-Kutta)等。
在这个过程中,需要将连续系统的状态方程离散化,即将连续时间步长的微分方程转化为离散时间步长的离散方程。
求解离散方程可采用递推的方式,根据系统的初始条件和上一时刻的状态变量值,计算出当前时刻的状态变量值。
以下是一个求解连续系统状态变量方程的步骤:1. 确定连续系统的状态变量方程。
例如,给定线性定常系统dx/dt = Ax + Bu,其中x为状态变量,A和B为系统矩阵。
2. 离散化。
将状态变量方程转化为离散方程。
常见的离散化方法有前项差分变换、后项差分变换和Tustin变换。
具体变换方法取决于系统的特性以及所需的数值稳定性和精度。
例如,使用Tustin变换将连续系统离散化,得到离散状态方程x[k+1] = A*x[k] + B*u[k]。
3. 初始化。
给定初始条件,如x[0] 和u[0],初始化状态变量值。
4. 数值求解。
使用数值方法(如龙格-库塔法)递推计算离散方程,得到一系列状态变量值x[1], x[2], ...,以及对应的输出值y[1], y[2], ...。
5. 分析结果。
根据求解得到的状态变量值和输出值,分析系统的性能,如稳定性、收敛速度等。
在MATLAB中,可以使用ode45等函数求解连续系统的状态变量方程。
以下是一个简单的示例:```MATLAB定义系统矩阵A、B和输入信号uA = [1 0; -1 1];B = [0 1];u = [1; 0.5];定义初始条件x0 = [1; 2];设置求解参数tspan = [0, 10];options = odeset('RelTol', 1e-6, 'AbsTol', 1e-6);求解状态变量方程[x, u] = ode45(@(t, x) A*x + B*u, tspan, x0, options);绘制状态变量曲线figure;plot(t, x(:, 1), 'b', 'LineWidth', 2);hold on;plot(t, x(:, 2), 'r', 'LineWidth', 2);xlabel('Time');ylabel('State Variables');legend('x1', 'x2');```这个示例中,我们使用ode45函数求解了一个线性定常系统在给定输入信号下的状态变量演化。
现代控制理论知识点汇总

1.状态空间表达式n 阶DuCx y Bu Ax x+=+= 1:⨯r u 1:⨯m y n n A ⨯:r n B ⨯:n m C ⨯:rm D ⨯:A 称为系统矩阵,描述系统内部状态之间的联系;B为输入(或控制)矩阵,表示输入对每个状态变量的作用情况;C 输出矩阵,表示输出与每个状态变量间的组成关系,D直接传递矩阵,表示输入对输出的直接传递关系。
2.状态空间描述的特点①考虑了“输入-状态-输出”这一过程,它揭示了问题的本质,即输入引起了状态的变化,而状态决定了输出。
②状态方程和输出方程都是运动方程。
③状态变量个数等于系统包含的独立贮能元件的个数,n 阶系统有n 个状态变量可以选择。
④状态变量的选择不唯一。
⑤从便于控制系统的构成来说,把状态变量选为可测量或可观察的量更为合适。
⑥建立状态空间描述的步骤:a 选择状态变量;b 列写微分方程并化为状态变量的一阶微分方程组;c 将一阶微分方程组化为向量矩阵形式,即为状态空间描述。
⑦状态空间分析法是时域内的一种矩阵运算方法,特别适合于用计算机计算。
3.模拟结构图(积分器加法器比例器)已知状态空间描述,绘制模拟结构图的步骤:积分器的数目应等于状态变量数,将他们画在适当的位置,每个积分器的输出表示相应的某个状态变量,然后根据状态空间表达式画出相应的加法器和比例器,最后用箭头将这些元件连接起来。
4.状态空间表达式的建立1由系统框图建立状态空间表达式:a 将各个环节(放大、积分、惯性等)变成相应的模拟结构图;b 每个积分器的输出选作i x ,输入则为i x;c 由模拟图写出状态方程和输出方程。
2由系统的机理出发建立状态空间表达式:如电路系统。
通常选电容上的电压和电感上的电流作为状态变量。
利用KVL 和KCL 列微分方程,整理。
③由描述系统的输入输出动态方程式(微分方程)或传递函数,建立系统的状态空间表达式,即实现问题。
实现是非唯一的。
方法:微分方程→系统函数→模拟结构图→状态空间表达式。
现代控制理论(第二章)讲解

sI
A 1
s 2
s3
1 1 s 3
(s
1)(s 2
2)
(s 1)(s 2)
1
(s
1)(s s
2)
(s 1)(s 2)
s3
e At
L1
(s
1)( s 2
2)
(s 1)(s 2)
EAST CHINA INSTITUTE OF TECHNOLOgy
第二章 控制系统状态空间表达式的解
2.1 线性定常齐次状态方程的解(自由解) 2.2 矩阵指数函数——状态转移矩阵 2.3 线性定常系统非齐次方程的解 2.4 * 线性时变系统的解 2.5 * 离散时间系统状态方程的解 2.6* 连续时间状态空间表达式的离散化
(s
1)( s 2
2)
(s 1)(s 2)
1
(s
1)( s s
2)
(s 1)(s 2)
eAt L1
sI A 1
2et e2t 2et 2e2t
et e2t
et
2e2t
et
2e2t
例2-6,利用凯莱-哈密顿定理— -----------------自学! 例2-3与例2-7也请注意自学!
EAST CHINA INSTITUTE OF TECHNOLOgy
2.3 线性定常系统非齐次方程的解
现在讨论线性定常系统在控制作用 方程为非齐次矩阵微分方程:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x1[(k
x2[(k
1)] 1)]
1 0
1
e
eT
T
x1 x2
(kT) (kT)
T
eT 1 eT
1u(k
T
)
系令统 T=输20出e.1TT方秒程,e1T得系1e统yeT(离TkT散)xx化12((kk状xTT1)态)(k空T)间T1表1ee达TT0式1xxr12(k((kTkT)T))
x
0
0
5(1 e5t )
5(e5t
1)
x
5 0
5e5t 5(1 e5t
)u
试将它离散化,并求出输入和初始条件分别为
u(t) 10, x(0) 00时,方程在采样时刻的 近似解
解:(1)离散化,取T 0.2秒,t kT 0.2k
G(KT
)
I
TA(kT
)
1 0
0 1
0.20 0
5(1 ek )
k 1
x(k) (k)x(0) (k j 1)Hu( j)
j 1
二、线性时变系统状态方程的离散化 --按导数定义近似求出,也称近似计算方法
假设T很小T≤0.1Tmin(最小时间常数),精度要 求不高时,可用差商代替微商。
t kT:
x(t) lim x(t t) x(t)
t 0
t
求取[kT , (k 1)T ]区间的导数
5(ek
1)
1 0
1 ek
ek
H (kT ) TB(kT ) 0.205
5ek 5(1 ek )
1 0
ek
1
ek
代入x[(k 1)T ] G(kT )x(kT ) H (kT )u(kT ) 得:离散化方程为
x1[(k x2[(k
1)T 1)T
] ]
1 0
1
ek ek
1 0
0.631 0.370
1 0
0.370 0.631
1.37 0.63
递推求下去
x1(0.6) x2 (0.6)
1 0
0.8651.37 0.1350.63
1 0
0.1350 0.8651
2.05 0.95
三、计算机控制系统的状态空间表达式 (一)计算机控制系统的组成
连续部分:保持和被控对象串联 离散部分:数字计算机
y(k T) x1 (k T) 1
0
x1 x2
(k T) (k T)
x1 (k
x2
(k
1)T 1)T
0.995 0.095
0.095 x1 (k T)
0.905
x2
(k
T
)
0.005 0.095r(k T)
y(kT) 1
0
x1 x2
(k T) (k T)
方法2、近似离散化 A(kT)=A定常 B(kT)=B
0.9 0.1
0.1 0.9
x1(kT x2 (kT
) )
00.1r
(kT
)
两种方法得 状态空间表
输出y(kT ) 1
0
x1(kT x2 (kT
) )
达式近似相 等。
离散方程求解可按2.3递推法或Z变换求解
一、线性定常系统状态方程的离散化
-(按非齐次状态方程解,求出)
线性定常系统状态方程的解为:
t
x(t) (t t0 )x(t0 )
(t )Bu ()d
t0
取t0 kT, t (k 1)T, u() u(kT) 常数
x([(k 1)T ] (T )x(kt) k(Tk1)T [(k 1)T ]Bu(kT )d
令G(T ) (T ) e AT
H (T ) 设t
(k
k(Tk 1)T e A[(k 1)T ]
1)T , dt d
Bd
下限 kT ,相当于t T
上限=(k+1)T ,相当于t 0
则:H (T ) 0T e AT Bdt 0T (t)Bdt
得连续离散化方程 :
x([(k 1)T ] G(T )x(kT ) H (T )u(kT )
x(t) lim x[(k 1)T ] x(kT )
T 0
T
x(kT ) x[(k 1)T ] x(kT ) A(kT )x(kT ) B(kT )u(kT ) T
x[(k 1)T ] [I TA(kT )]X (kT ) TB(kT )u(kT ) x[(k 1)T ] G(kT )x(kT ) H (kT )u(kT ) G(kT ) I TA(kT ) H (kT ) TB(kT )
)
例2.5已知控制对象满足
x
0 0
解:
1 2
x
10u,求其离散化方程
(1)(t)
L1[SI
A]1
1
0
1 / 2(1 e2t )
e2t
1
1 / 2(1 e2t )
(2)G(T)
(t)
tT
0
e2t
T 1
(3)H(T)
0
0
1/ 2(1 e2t )0 T 1
e2t
1dt
0
0
1/ 2(1 e2t
x1 x2
0 0
1 1
x1 x2
0 1u
y x1 1
0
x1 x2
说明:
u(t)是零阶保持器的输出,即u(kT)=常数
满足假设,可离散化
方法1、线性定常系统离散化
(1)a、e At
L1[sI
A]1
1 0
1 et
et
b、G(t)
eAT
1 0
1 eT
eT
c、H
(T
)0T
e
AT
(二)连续部分离散化,求被控对象离散化状 态方程。
(三)系统的离散化状态空间表达式:
根据系统结构确定系统的离散状态方程和输出 方程。特点u(kT)=r(kT)-y(kT)=r(kT)-Cx(kT), 例2.7 求如图所示的计算机控制系统的状态方程
解:对象 1 的状态方程和输出方程为
s(s 1)
比较:
当 G(kT ) (T ) eAT I AT 1 (AT )2 I AT
2!
T的值越小,近似程度越高
又
H( kT)
0T
eAT Bdt
0T [I
At
1 ( At)2 2!
]Bdt
T很小,t就很小,将包含t的各式略去
0T I B dt BT
结论:上式为近似计算方法
例2.6 已知时变系统
即t kT时刻,y(kT ) Cx(kT ) Du(kT )
离散后C与D不改变
归纳:将连续状态方程离散化步骤
1、求(t)=eAt L1[SI A]1
2、G(T ) (T ) (t) t T
3、求H (T 4、求x[(k
) 0T eAtBdt
1)T ] G(T
)x(kT
)
H
(T
)u(kT
e2t
) dt
1 4
(2T e2T 1 (1 e2T )
1)
2
(4)xx12[[((kk
1)T] 1)T]
G(T)xx12
(kT) (kT)
H(.5秒)G(t)和
H(t)都是确定的系数矩阵
(2)离散化后得状态方程,可按递推法或
Z变换法求出解
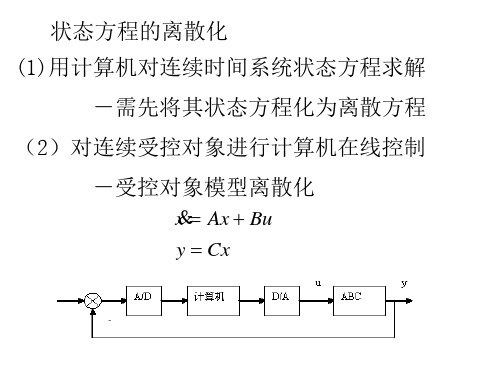
2.6 连续时间系统状态方程的离散化 (1)用计算机对连续时间系统状态方程求解
-需先将其状态方程化为离散方程 (2)对连续受控对象进行计算机在线控制
-受控对象模型离散化
x Ax Bu y Cx
假设:(1)t=kT,T为采样周期,且很 小,k=0,1,2…为一正整数
(2)u(t)只在采样时离散化,即在 kt≤t≤(k+1)T,u(t)=u(kT)=常数,0阶保持
a、G(kT
)
I
TA
1 0
T 1 T
b、H
(kT
)
TB
0 T
x1[(k x2[(k
1)T ] 1)T ]
1 0
T 1
t
x1(kT x2 (kT
) )
0 T
u(kT
)
u(kT ) r(kT ) x1(kT )
系统离散状态方程(T=0.1)
可见T较小时,
x1[(k x2[(k
1)T ] 1)T ]
Bdt
0T
1 0
1
et et
10dt
T
eT 1 eT
1
d、x[(k 1)T ] G(T )x(kT ) H(T )u(kT )
1 0
1
eT eT
x1(kT x2 (kT
) )
T
eT 1 eT
1u(kT
)
(2)由u(kT)=r(kT)-y(kT)=r(kT)-x1 (kT),代入,得系统的离散化 状态方程。
x1(kT x2 (kT
) )
1 0
1
ek ek
u1(kT u2 (kT
) )
(2)用递推法求离散方程的近似解:
取k=0,1,2…T=0.2秒,并代入输入函数和 初始条件可得近似解:
x1(0.2) x2 (0.2)
1 0
00 10
1 0
10 01
1 0
x1(0.4) x2 (0.4)
