试验一谐波分析试验File
实验一谐波分析实验

实验一--谐波分析实验- 1 -实验一 谐波分析实验(波形分解、合成不失真条件研究)一、实验目的1.了解分解、合成非正弦周期信号的物理过程。
2.观察合成某一确定的周期信号时,所必须保持的合理的频率结构,正确的幅值比例和初始相位关系。
二、实验原理对某一个非正弦周期信号X (t ),若其周期为T 、频率为f ,则可以分解为无穷项谐波之和。
即∑∞=++=10)2sin()(n n n t TnA a t x φπ ∑∞=++=100)2sin(n n n t nf A a φπ (1-1)上式表明,各次谐波的频率分别是基波频率0f 的整数倍。
如果f (t )是一个锯齿波,其波形如图1.1所示,则其数学表达式为:)21()()(0,2)(-=+≤≤-=t x nT t x Tt E t T E t x对f (t )进行谐波分析可知 πφπ===n n nEA a ,2,00 所以- 2 -∑∑∞=∞=+=+=101)2sin(2)2sin(2)(n n t nf n Et Tn n E t x ππππππ)31(,...])2(2sin[21)2sin(200-⎭⎬⎫⎩⎨⎧++++=πππππt f t f E即锯齿波可以分解成为基波的一次、二次…n 次…无数项谐波之和,其幅值分别为基波幅值的n 1,且各次谐波之间初始相角差为零(基波幅值为π2E)。
反过来,用上述这些谐波可以合成为一个锯齿波。
同理,只要选择符合要求的不同频率成份和相应的幅值比例及相位关系的谐波,便可近似地合成相应的方波、三角波等非正弦周期波形。
三、实验内容及操作步骤利用计算机及Excel 、Matlab 或其它应用软件完成下面的工作: 1.合成方波① 观察基波与三次谐波幅值分别为1、1/3,相位差为零时的合成波波形; ② 再分别将5次、7次、9次…谐波叠加进去(各次谐波的幅值为1/n ,注意各次谐波与基波间的相位关系),观察并记录合成波的波形,找出合成波的形状与谐波次数之间有何关系。
示波器谐波分析实验报告

(1)从信号发生器输出一个正弦信号到CH1,设好信号的输出幅度及频率,调节示波器Time/div按钮,使波形显示幅度合适、显示一两个稳定的正弦波,记下频率f和峰值电压Vp-p.
(2)利用网格线测出正弦波的波峰到波谷的垂直距离dy,并记录Vol/div的值
(3)计算Vp-p=a*dy
五、数据处理:
次数
dy
V/div
Vpp
1
5.2cm
0.2V/cm
1.04V
2
2.1cm
0.5V/cm
1.05V
次数
dx
T/div
T
1
1.9cm
5ms/cm
9.5ms
2
3.8cm
2.5ms/cm
9.5ms
fx(Hz)
fy(Hz)
图形
nx
ny
fx:fy
nx:ny
1
100
100
1
1
1:1
1:1
2
100
200
2、双踪示波器的原理:电子开关使两个待测电压信号YCH1和YCH2周期性地轮流作用在Y偏转板,这样在荧光屏上忽而显示YCH1信号波形,忽而显示YCH2信号波形。由于荧光屏荧光物质的余辉及人眼视觉滞留效应,荧光屏上看到的是两个波形。当扫描信号的周期与被测信号的周期一致或是整数倍,屏上一般会显示出完整周期的正弦波形。
3.将两信号分别接入CH1和CH2,对应做好记录。将示波器的屏幕显示波形,选择列表里,选中CH1,CH2下的X-Y。
4.不能;同步旋钮是使每次扫描都扫描同一个起始相位,使一个示波器内只有一个稳定的图形,但从李萨如图形的形成原理来看,调同步旋钮式不能使它稳定下来的。应该是调频率。
新能源汽车教学实验系列:谐波分析实验及习题思考

文库资料 ©2016 Guangzhou ZHIYUAN Electronics Stock Co., Ltd.文章源自ZLG 致远电子,转载或引用请注明出处1 谐波分析实验及习题思考一、实验目的1、检测电机在不同负载运行状态下的50次谐波畸变率及各次谐波幅值2、分析电机控制器输出电力的品质。
二、实验步骤1、检查系统。
检查系统接线,电源电压是否正常,插座是否已经插好,如无异常,开启控制柜电源,打开电机测试软件,查看控制柜绿灯是否点亮,完成后系统准备就绪。
2、进入测试界面。
查看配置信息,是否和实际的信息一致,如果一致即可进入测试阶段。
打开,进入开放测试界面,点击按钮启动开放测试。
这时,如果有勾选更新数据选项,数据显示栏将会有部分数据显示跳动;如无,只需要将更新数据选项勾选上,即可在数据显示栏里显示数据。
图19.1 勾选使能与更新数据3、点击使能负载和使能被测,在负载转速和油门比例输入栏里边输入数据,在“负载转速(rpm )”输入栏里边输入“600”,然后“回车”,速度稳定后后在“油门比例(%)”的输入栏里边输入“20”然后“回车”。
4、通过功率分析仪,查看并记录驱动器输出的谐波畸变率,谐波幅值等相应的数据(具体操作请查看功率分析仪的使用手册)。
5、改变运行状态,测试不同运行状态下的谐波畸变率和相关参数。
注意:调节油门时,避免调节跨度太大,以免PID 过程中损坏设备。
如果发生电机运行状态异常,请立即结束测试,有必要时请按下红色急停开关。
6、根据已有的数据分析电机控制器的输出电力品质。
三、实验总结和思考1、驱动器输出的谐波畸变率,谐波幅值等相应数据和电机的运行状态有什么关系?2、驱动器输出为什么会存在谐波,跟驱动器驱动的算法有什么关系?查找资料是否有办法降低谐波畸变率?。
谐波检测方法分析

的时频局部化分析方法。这就是说在高频部分具有较低的频率 分辨率和较高的时间分辨率 ,在低频部分具有较低的时间分辨 率和较高 的频率分辨率 ,不但可 以应用于平稳信号 ,而且可 以 应 用于分析非平稳信号。利用离散小波变换可 以将信号分解到
学术研讨 l 1 1 5
信号 分解 的结果 ,使用多分辨率 的概念 ,低频段 的结果不含谐 波的基波分量 。利用该算法可以使用软件进行谐波检测 ,该方
法 计 算速 度 快 ,可 以快 速 跟 踪谐 波 的 变 化 。 但它 也 有 固 有 的缺
陷 ,反映在窗 口能量不集中 ,有频率重叠现 象 ,需要找到能量 集 中、分 频严格 的小波函 数。 目前 ,尚未 出现理 想的小波 函 数。多分辨率分析是小波变化 的一个特点 ,并且在时域和频域
用。
谐 波 检 测 方 法 分 析
◇ 陕西铁 路 工程 职业技 术 学 院 王语 园
随着 电力 电子器件 的大量使 用 ,电力系统 谐波污染 日益
利用神经网络进行谐波测量 ,即使 用神经元来代替带通或
带 阻 滤 波 器检 测 法 中 的带 通 滤 波 器 和检 波 器 。待 测 量信 号 作 为 神 经 网络 的 输 入 ,相 当于 放 大 器 的 输 出信 号 。检 波器 的输 出信 号 对 应 神 经 网 络 的输 出 。通 过 这 种 方 法可 以得 到 所 要 测量 的各 次 谐 波 信 号 的 幅值 ,输 出为 零 就 可 以 判 断为 被 测 信号 中不 含 某 次谐波。
构建三相 电路 。这一方法主要优 点是 当电网 电压对称且无畸变
时 ,各电流分量的测量电路比较简单 ,并且延时少。 在这种方法 中,需要用到与瑚 电网 电压 e 同相位的余弦 信号一 c o s t 0 t  ̄ ' l l 对应的正弦信号s i n t o t ,它们可以由一个正 、余弦 信号发生器和一个锁相环得到。根据定义可以计算得 出 、 , 再经过低通滤波器 ( L P F) 滤波得出 f 、 。 的直流分量 z 、 。
谐波实验报告

实验一 谐波分析实验一、实验目的1)了解分解、合成非正弦周期信号的物理过程2)观察合成某一确定的周期信号时,所必须保持的合理的频率结构,正确的幅值比例和初始相位关系。
二、实验原理本实验主要运用傅立叶分解的方式对方波、锯齿波以及三角波进行分解与合成。
下面就对这三种波形的傅立叶分解原理进行介绍。
傅立叶分解原理对某一个非正弦周期信号X(t)(在有限区间上满足狄里赫利条件的函数),若其周期为T 、频率为f ,则可以分解为无穷项谐波之和。
即010100122()(cos sin )22sin()2sin(2)2n n n n n n n n n a n n x t a t b t T T a n A t T a A f t πππφπφ∞=∞=∞==++ =++ =++∑∑∑ 上式表明,各次谐波的频率分别是基波频率0f 的整数倍。
只要选择符合要求的不同频率成分和相应幅值比例及相位关系的谐波,便可近似地合成相应的方波、三角波等非正弦周期波形,以及任何在有限区间上满足狄里赫利条件的函数。
三、实验内容(一)方波1)方波的谐波分析,右图的一个方波(),022()0,2()()E T x t t T x t t T x t nT x t ⎧=≤≤⎪⎪⎪= ≤≤ ⎨⎪+=⎪⎪⎩进行谐波分析可知:00n a a ==/20/22()sin (1cos )2,1,3,5...0,2,4,6...T n T b x t n tdt T En n En n n ωπππ-= =-⎧ =⎪ =⎨⎪ =⎩⎰ 所以 000211()(sin sin 3sin 5...)35Ex t t t t ωωωπ=+++ 根据实验要求取基波的幅值为1,即212E E ππ=⇒=为了方便,可以取01ω=即方波可以展开成傅立叶级数为:11()(sin sin 3sin 5...)35x t t t t =+++2)合成方波根据讲义的讲解,编写以下程序实现功能要求 a 、一次谐波、三次谐波合成 x=0:4*pi/100:4*pi; y1=sin(x); y2=sin(3*x)/3;plot(x,y1,x,y2,x,y1+y2); grid onb 、一次谐波、三次谐波、五次谐波合成 x=0:4*pi/100:4*pi;y1=sin(x);y2=sin(3*x)/3;y3=sin(5*x)/5;plot(x,y1,x,y2,x,y3,x,y1+y2+y3);grid on之后的谐波合成类似,省略程序,得到的合成方波分别如图所示一次谐波、三次谐波、五次谐波、七次谐波合成方波一次谐波、三次谐波、五次谐波、七次谐波、九次谐波合成方波总结:方波可以通过谐波的叠加得到,叠加的谐波级次越高,方波的失真越小。
谐波测试报告范文

谐波测试报告范文一、引言谐波是指在周期性信号中出现的频率高于基波频率的分量。
对于电力系统而言,谐波是一种很常见的问题,它可能引起电力设备的故障、损坏,甚至对用户造成干扰。
因此,对电力系统中的谐波进行检测与分析是非常重要的。
本报告将对一些电力系统进行谐波测试,并对测试结果进行详细分析,以期帮助用户了解该电力系统中的谐波情况,并制定相应的解决方案。
二、测试内容本次谐波测试主要包含以下内容:1.测试环境:测试电力系统的主要参数和拓扑结构。
2.测试设备:使用的仪器设备,包括谐波测试仪、电能质量分析仪等。
3.测试方法:测试仪器的使用方法以及测试过程中的注意事项。
4.谐波测试结果:对测试数据进行分析和总结,包括谐波程度、谐波频率和谐波含量等。
5.结果分析:根据测试结果对电力系统谐波问题的原因进行分析,并提出相应的改进方案。
三、测试环境测试对象电力系统,该电力系统为三相四线制,供电电源为220V/380V,50Hz。
其中,谐波测试点包括发电机、变压器、配电线路等。
四、测试设备本次测试使用了谐波测试仪和电能质量分析仪两种设备。
谐波测试仪用于对电力系统中的谐波进行定量分析,电能质量分析仪则可以对谐波进行定性分析。
五、测试方法1.连接测试仪器:首先,将谐波测试仪和电能质量分析仪与电力系统相应部位进行连接,确保测试仪器可以获取准确的数据。
2.预热与校准:打开测试仪器的电源,进行预热和校准,确保测试结果的准确性。
3.测量参数:根据测试需求,设置测试仪器的相应参数,例如测试频率范围、采样率等。
4.进行测试:根据测试计划,对电力系统中的关键部位进行测试,并记录测试数据。
5.数据分析:将测试数据导入电脑,使用专业软件对数据进行分析,包括谐波程度、谐波频率和谐波含量等。
6.结果总结:根据数据分析结果,对电力系统中的谐波问题进行总结,并提出相应的改进方案。
六、谐波测试结果经过对电力系统中的谐波进行测试和数据分析,我们得到了以下结果:1.谐波程度:对电力系统的各个测试点进行谐波分析,发现谐波程度较高的有变压器和一些配电线路。
谐波分析报告

谐波分析报告报告编号:HA-2021-001报告时间:2021年5月10日报告人:XXX公司电力设计研究院摘要:本报告主要对XXX变电站进行了谐波分析,通过测量数据和分析,发现变电站内存在谐波扰动,且谐波含量较高。
我们提出了相应的措施,以减轻谐波扰动对电力质量带来的影响。
一、谐波分析1.1 测点布置本次谐波分析以XXX变电站为研究对象,共设立4个测点,分别布置于主变、母线、电容器组和主变出线。
如下图所示:[插入布置图]1.2 测量数据通过谐波分析仪进行谐波测试,得到测量数据如下表所示:[插入数据表]1.3 谐波分析根据测量数据,我们对变电站的谐波情况进行了分析。
测试结果显示,变电站内谐波含量较高,其中3、5、7次谐波含量占比较大,分别为15.24%、26.98%、33.76%。
此外,还存在较多的9次、11次、13次等高次谐波,占比分别为7.09%、6.62%、5.34%。
这些谐波扰动将会对电力质量产生一定影响。
二、措施建议2.1 添加滤波器针对电容器组及其电抗器,我们建议添加谐波滤波器。
通过滤波器来控制电容器组及其电抗器的谐波电流,减少谐波扰动。
2.2 替换谐波产生源变电站内谐波扰动的主要产生源为电容器组、逆变器及大功率电子设备。
建议对这些设备进行替换,选择质量更好的设备,以减少谐波的产生。
2.3 增加接地电阻适当增加接地电阻,以减少谐波在地网中的扩散。
三、结论本次谐波分析显示,XXX变电站内存在较高的谐波含量,将对电力质量产生一定影响。
建议采取上述措施,减轻谐波扰动对电力质量的影响。
同时,在以后的运营中,应定期对变电站进行谐波监测,及时发现故障并进行处理。
谐波分析实验报告
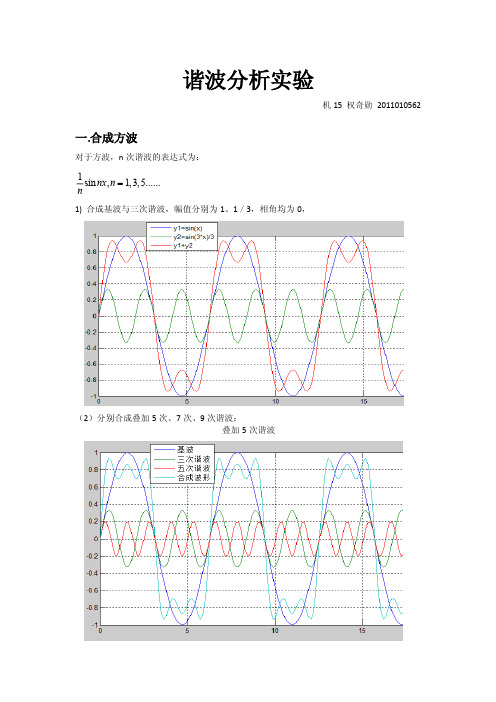
谐波分析实验机15 权奇勋2011010562一.合成方波对于方波,n次谐波的表达式为:1sin nx,n=1,3,5......n1) 合成基波与三次谐波,幅值分别为1、1/3,相角均为0,(2)分别合成叠加5次、7次、9次谐波:叠加5次谐波叠加7次谐波叠加9次谐波通过观察波形,发现:叠加谐波次数越高,合成波形越趋近于方波。
(3)分别改变3、5次谐波与基波间的相角,研究谐波间相角改变对合成波形的影响将3次谐波的初相角改为-π/2将5次谐波的初相角改为-π/2分析结论:改变谐波与基波间的相角,会使合成波形与方波相比有较大的失真。
且改变相角的谐波次数越低,失真越大。
(4)分别改变3、5次谐波与基波间的幅值比例关系,研究谐波间幅值比例改变对合成波形的影响3次谐波幅值改为(1/3)×2=2/35次谐波幅值改为(1/5)×2=2/5分析结论:改变谐波的幅值,会使合成波形与方波相比产生失真;且幅值改变的倍率相同的情况下,改变谐波的次数越低,失真越大。
二.合成锯齿波(最高谐波次数选为9)对于锯齿波,n次谐波的表达式为:π1nx+p),n=1,2,3......1)合成波的形状与谐波次数的关系叠加2次谐波叠加4次谐波叠加9次谐波通过观察波形,发现:叠加谐波次数越高,合成波形越趋近于锯齿波。
(2)分别改变2、4次谐波与基波间的幅值比例关系2次谐波的幅值改为(1/2)×2=14次谐波的幅值改为(1/4×2)=1/2分析结论:改变谐波的幅值,会使合成波形与锯齿波相比产生失真;且幅值改变的倍率相同的情况下,改变谐波的次数越低,失真越大。
(3)分别改变2、4次谐波与基波间的相角2次谐波的初相角改为pi+pi/2=3pi/24次谐波的初相角改为pi+pi/2=3pi/2分析结论:改变谐波与基波间的相角,会使合成波形与锯齿波相比有较大的失真。
且改变相角的谐波次数越低,失真越大。
三.合成三角波(最高谐波次数选为9)对于三角波,n次谐波的表达式为:π×π1nx,n=1,3,5......1)合成波的形状与谐波次数的关系叠加3次谐波叠加5次谐波叠加9次谐波通过观察波形,发现:叠加谐波次数越高,合成波形越趋近于三角波。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 谐波分析实验
(波形分解、合成不失真条件研究)
一、实验目的
1.了解分解、合成非正弦周期信号的物理过程。
2.观察合成某一确定的周期信号时,所必须保持的合理的频率结构,正确的幅值比例和初始相位关系。
二、实验原理
对某一个非正弦周期信号X (t ),若其周期为T 、频率为f ,则可以分解为无穷项谐波之和。
即
∑∞=++=10)2sin(
)(n n n t T
n A a t x φπ ∑∞
=++=100)2s i n (n n n t nf A a φπ (1-1)
上式表明,各次谐波的频率分别是基波频率0f 的整数倍。
如果f (t )是一个锯齿波,其波形如图1.1
)21()()(0,2)(-=+≤≤-=t x nT t x T t E t T E t x 对f (t )进行谐波分析可知 πφπ===n n n E A a ,2,00 所以 ∑∑∞=∞=+=+=1
01)2s i n (2)2s i n (2)(n n t nf n E t T n n E t x ππππππ
)31(,...])2(2sin[21)2sin(200-⎭⎬⎫⎩⎨⎧++++=πππππt f t f E
即锯齿波可以分解成为基波的一次、二次…n 次…无数项谐波之和,其幅值分别为基波幅
值的n 1,且各次谐波之间初始相角差为零(基波幅值为
2E )。
反过来,用上述这些谐波可以合成为一个锯齿波。
同理,只要选择符合要求的不同频率成份和相应的幅值比例及相位关系的谐波,便可近似地合成相应的方波、三角波等非正弦周期波形。
三、实验内容及操作步骤
利用计算机及Excel 、Matlab 或其它应用软件完成下面的工作:
1.合成方波
① 观察基波与三次谐波幅值分别为1、1/3,相位差为零时的合成波
波形;
② 再分别将5次、7次、9次…谐波叠加进去(各次谐波的幅值为1/n ,注意各次谐波与基波间的相位关系),观察并记录合成波的波形,找出合成波的形状与谐波次数之间有何关系。
③ 分别改变3次、5次谐波与基波间的相角,研究谐波间相角改变对合成波形的影响,并记录波形。
④ 分别改变3次、5次谐波与基波间的幅值比例关系,研究谐波间幅值比
例改变对合成波形的影响,并记录波形。
2.合成锯齿波
参照合成方波的步骤(选择最高次谐波数不得低于9),研究各谐波间的幅值、相位关系,并与方波做比较,记录波形。
3.合成三角波
参照合成方波的步骤(选择最高次谐波数不得低于9),研究各谐波间的幅值、相位关系,并与方波、锯齿波做比较,记录波形。
四、实验报告要求
1.记录下每一步骤下的不同波形,将谐波与合成波形用不同色彩绘在同一图上,并加以说明。
2.讨论以下问题
① 在合成波形时,各次谐波间的相角关系与幅值比例关系,哪一个对合成波形的影响大?
② 如果用正弦波去合成波形,在合成三角波时,三次谐波的相位与合成方波、锯齿波时的相位是否一样?
③ 在一般的常规应用中,对于100HZ 的方波、锯齿波及三角波信号,你认为所应考虑的频段范围各应为多少?
3.回答下列思考题。
(1)如果将图1.1 所示的锯齿波仅把坐标移
一下使之成为图1.3
并比较二者同异之处。
(2
如何保证?用什么方法观察调节?
(3)当锯齿波合成后,如果将1、3、5
是什么样,该信号的频率为多少?。
