电子测量技术(第二版)林占江课后答案
电子测量技术课后习题答案
2．4 有一个100V 的被测电压，假设用0.5级、量程为0-300V 和1.0级、量程为0-100V的两只电压表测量，问哪只电压表测得更准些？为什么？答： 要判断哪块电压表测得更准确，即判断哪块表的测量准确度更高。
〔1〕对量程为0-300V 、±0.5级电压表，根据公式有%100%%1001⨯•≤⨯∆=xs x x xm x γ %5.1%100100%5.0300=⨯⨯=〔2〕对量程为0-100V 、±1.0级电压表，同样根据公式有%100%%1002⨯•≤⨯∆=xs x x xm x γ %0.1%100100%0.1100=⨯⨯=从计算结果可以看出，用量程为0-100V 、±1.0级电压表测量所产生的示值相对误差小，所以选用量程为0-100V 、±1.0级电压表测量更准确。
2．9 测量上限为500V 的电压表，在示值450V 处的实际值为445V ，求该示值的： 〔1〕绝对误差〔2〕相对误差〔3〕引用误差〔4〕修正值 答：〔1〕绝对误差V V V A x x 5450445-=-=-=∆ 〔2〕相对误差%12.1%1004455%100-=⨯-=⨯∆=x x x γ 〔3〕引用误差%0.1%1005005%100-=⨯-=⨯∆=m m x x γ 〔4〕修正值V x c 5=∆-=2．10 对某电阻进行等精度测量10次，数据如下〔单位k Ω〕：0.992、0.993、 0.992、 0.991、 0.993、 0.994、 0.997、 0.994、 0.991 、0.998。
试给出包含误差值的测量结果表达式。
答：1〕．将测量数据按先后次序列表。
2〕．用公式∑=nii x n x 1求算术平均值。
9935.010998.0993.0992.0)(11011021=+++=+++=∑ V V V n x3〕．用公式x x i i -=ν求每一次测量值的剩余误差，并填入上表中。
电子测量技术-课后答案(教育类别)
fx
Tfc fc
校园类
22
第四章 习题
校园类
23
4-1 示波器荧光屏观测到峰值均为1V的正弦波、方波 和三角波。分别采用峰值、有效值及平均值方式， 按正弦波有效值刻度的电压表测量，测量结果是？
解（1）峰值表读数
三种波形在峰值表上的读数均为 1/ 2 0.707V
（2）均值表的读数
均值表以正弦波有效值刻度时，其读数a K f V
v
10
可见，选用15V、1.5级电压表测量更合适
校园类
2
2-8 用电压表和电流表测量电阻值可用下图电路
(a)
(b)
设电压表内阻为Rv，电流表内阻为RA，求 被测电阻R的绝对误差和相对误差？这两 种电路分别适用于测量什么范围的内阻？
校园类
3
解：设被测电阻真值为 Rxo 对于图（a）
V
V
给出值： Rx I V V
解：（1）用第一种方法，求得
R1 100.33 (R1) 0.0054
( R1 )
( R1 ) 8
0.0160
校园类
13
用第二种方法，求得 R2 100.31
(R2 ) 0.0261
(R2
)
(R2 6
)
0.0106
由计算结果可见第二种方法可靠
校园类
11
（1）用莱布准则判别：
3 (x) 95.5656 v0 没判别出异常数据
（2）用格拉布斯准则判别：
n=8，查表得P=99%时，g=2.32
《测试技术》(第二版)课后习题标准答案--
解：（1） 瞬变信号－指数衰减振荡信号，其频谱具有连续性和衰减性。
（2） 准周期信号，因为各简谐成分的频率比为无理数，其频谱仍具有离散性。
（3） 周期信号，因为各简谐成分的频率比为无理数，其频谱具有离散性、谐波性和收敛性。
解：x(t)=sin2t f 0π的有效值（均方根值）：2/1)4sin 41(21)4sin 41(21)4cos 1(212sin 1)(10000000000000202000=-=-=-===⎰⎰⎰T f f T T tf f T T dt t f T dt t f T dt t x T x T T T T rms ππππππ 解：周期三角波的时域数学描述如下：（1）傅里叶级数的三角函数展开：，式中由于x(t)是偶函数，t n 0sin ω是奇函数，则t n t x 0sin )(ω也是奇函数，而奇函数在上下限对称区间上的积分等于0。
故=n b 0。
因此，其三角函数展开式如下：其频谱如下图所示：T 0/2-T 0/21x (t ) t. . . . . .⎪⎪⎪⎩⎪⎪⎪⎨⎧+≤≤-≤≤-+=)(202022)(00000nT t x T t t T AA t T t T A A t x 21)21(2)(12/0002/2/00000=-==⎰⎰-T T T dt t T T dt t x T a ⎰⎰-==-2/00002/2/00000cos )21(4cos )(2T T T n dt t n t T T dtt n t x T a ωω⎪⎩⎪⎨⎧==== ,6,4,20,5,3,142sin 422222n n n n n πππ⎰-=2/2/0000sin )(2T T n dtt n t x T b ω∑∞=+=1022cos 1421)(n t n nt x ωπ∑∞=++=1022)2sin(1421n t n nπωπ(n =1, 3, 5, …）（2）复指数展开式复指数与三角函数展开式之间的关系如下：故有)( 21=212121n 22000=-===+====nn n e n m n n n n n a barctg C R C I arctg a A b a C a A C φ 0ωA (ω)ω0 3ω0 5ω0 0ωω0 3ω0 5ω0 ϕ (ω)24π294π2254π 21 2π C 0 =a 0C N =(a n -jb n )/2 C -N =(a n +jb n )/2 R e C N =a n /2 I m C N =-b n /2)(212122000n n n e n m n n n n n a barctg C R C I arctg A b a C a A C -===+===φ R e C N =a n /2⎪⎩⎪⎨⎧====,6,4,20,5,3,122sin 222222n n n n n πππI m C N =-b n /2 ＝0单边幅频谱 单边相频谱0 ωn φω0 3ω0 5ω0 -ω0 -3ω0 -5ω0 0 ωω0 3ω0 22π 21 292π2252π5ω0 -ω0 -3ω0 292π2252π-5ω0 22πnC0 ωI m C nω0 3ω0 5ω0 -ω0 -3ω0 -5ω0 0 ωR e C nω03ω0 22π21 292π2252π 5ω0 -ω0 -3ω0 292π 2252π-5ω0 22π虚频谱双边相频谱实频谱双边幅频谱解：该三角形窗函数是一非周期函数，其时域数学描述如下：用傅里叶变换求频谱。
电子测量技术 作业答案
作业1. 现代数字化测量系统的基本构成环节有: (传感器) 、(调理电路) 、(数据采集系统)、CPU 和显示部分。
2. 测量系统的静态特性可以用（函数解析式）、（表格）和（曲线）方式来表示。
表征测量系统静态特性的主要指标有（灵敏度）、（非线性度）、（回程误差）等。
3．一阶测量系统的动态特性主要由时间常数 τ来决定。
当输入信号角频率ω=1/τ时，一阶测量系统的幅值下降（ 3 ）dB ，此时的输入频率称为（ 转折频率）。
1 根据误差的性质和特点不同，可以将测量误差分（系统误差）、（随机误差）和（粗大误差）。
2 随机误差的统计学特性有(有界性)、(单峰性)、(对称性)、和(补偿性)。
3 检定2.5级（即最大引用误差为2.5%）的全量程为100V 的电压表，发现50V 刻度点的示值误差2V 为最大误差，问该电表是否合格？ 答: 合格 %5.2%2%1001002<=⨯1. 直接测量方法和间接测量方法有何不同？答: 直接测量: 被测量可以通过测量仪表给出的测量示值直接得到;间接测量: 被测量与可测量量之间存在已知的某种确定数学关系, 通过计算得到.2.什么是测量系统的动态特性？表征测量系统动态特性的主要指标有哪些？它们是如何定义的？答: 动态特性反映的是测量系统对变化输入信号的快速响应的能力, 如可以用响应时间, 上升时间等来定量描述. 3. 一阶系统的时间常数是如何定义的？答: 给一阶系统施加一个阶越输入, 一阶系统的输出从零状态上升到稳态的63.2%所需时间.1.用量程为10A 的电流表，测量实际值为8A 的电流，若读数为8.1A ，求测量的绝对误差和相对误差。
若所求得的绝对误差被视为最大绝对误差，该电流表的准确度等级可定为哪一级？ 答: 绝对误差: 8.1-8.0=0.1A相对误差：%2.1%25.1%1000.80.81.8≈=⨯-（偶数法则）最大引用误差：%0.1%10010.81.8=⨯- 1.0级2. 进行下述计算，并给出适当的有效数字。
电子测量技术课后习题答案林占江版-17页文档资料
4.14 P144
4.15 0.05%, 20%
4.16 0.056% 4.17 100kHz, 40μs, 10
4.18 9.4ns 4.19 用外触发方式 4.20 滞后电源电压 45°
超前 45°
第5章 时域测量
5.1,5.2 参阅本间相关内容 5.3 李沙育图形，是圆形。 5.4 李沙育图形（1）椭圆形（2）“8”字形 5.5 被测信号频率与扫描信号频率不成整数倍，图形向左“跑动”。 5.6 被测信号频率与扫描信号频率不成整数倍，波形紊乱。 5.7 前沿有上冲，前沿弯曲。 5.8 最小周期T=0.2μs×10×10=20μs, 频率50k 5.9 最高工作频率是20MHz 5.10 最低工作频率是0.4Hz
2.14 正态分布,1215.01±6.11,
2.15 86.4, 3.18, 0.00312, 5.84E4
2.16 3.3, 38 2.17 mγA+n γB, ±9.5% 2.18 ±4% 2.19 160±0.16%, 9.4±1.0%, 2.20 ±5%, ±5% 2.21 2级
第3章模拟测量方法
第6章 频域测量
7.1 P236 7.2 P237 7.3 P238 7.4 P241 7.5 P243 7.6 P246 7.7 P249 7.8 P265
第7章 逻辑分析仪
8.1 P270 8.2 P272 8.3 P272 8.4 P274 8.5 P275 8.6 P276 8.7 P277
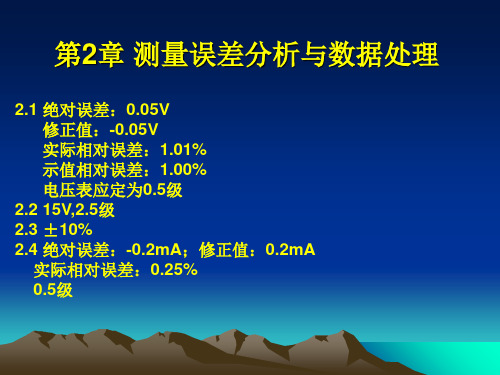
第2章 测量误差分析与数据处理
2.1 绝对误差：0.05V 修正值：-0.05V 实际相对误差：1.01% 示值相对误差：1.00% 电压表应定为0.5级
2.2 15V,2.5级 2.3 ±10% 2.4 绝对误差：-0.2mA；修正值：0.2mA
电子测量技术课后题答案
④判断： 测量次数为 9 次，置信概率 99%，查表可得 G=2.32
GS (V ) = 2.32 × 0.13 = 0.30
比较可得无残差大于 0.30 的数据 1.4 解： ①平均值
∴测得数据无异常
1 n 1 X i = (52.953 + 52.959 + 52.961 + 52.950 + 52.955 + 52.950 + 52.949 + 52.954 + 52.955) ∑ n i =1 9 = 52.954 X =
计算扩展不确定度. 参考答案: A 类评定: u1=0.084KΩ B 类评定: u2=0.019KΩ 合成标准不确定度为: uc = u12 + u2 2 = 0.086 K Ω
v=u4/( u14/v1+ u24/v2) ≈ 9 扩展不确定度评定,按 t 分布处理, 概率可取 95%, 查 t 分布表得到包含因子 扩展不确定度评定 U95=K95 uc =2.26x0.086=0.19 KΩ 完整的测量结果为:R=(13.40±0.19) KΩ (K95=2.26,P=95%) Veff=9 1.11 解：y= x1 x2 ⋅ x 3 3 =x 1 ⋅ x 2
20ns / div ~ 0.5s / div 10 20ns / div 显示一个周期波形时，被测信号的周期范围为 × 10div ~ 0.5s / div × 10div 10 即20ns ~ 5s 1 1 ~ ，即50 MHz ~ 0.2 Hz 则被测信号的频率范围为 20ns 5s 带有扫描扩展“×10”功能的示波器，其Dt的总范围为 2.17 解：
《测试技术》(第二版)课后习题答案
解：（1） 瞬变信号－指数衰减振荡信号，其频谱具有连续性和衰减性。
（2） 准周期信号，因为各简谐成分的频率比为无理数，其频谱仍具有离散性。
（3） 周期信号，因为各简谐成分的频率比为无理数，其频谱具有离散性、谐波性和收敛性。
解：x(t)=sin2t f 0π的有效值（均方根值）：2/1)4sin 41(21)4sin 41(21)4cos 1(212sin 1)(10000000000000202000=-=-=-===⎰⎰⎰T f f T T tf f T T dt t f T dt t f T dt t x T x T T T T rms ππππππ 解：周期三角波的时域数学描述如下：（1）傅里叶级数的三角函数展开：，式中由于x(t)是偶函数，t n 0sin ω是奇函数，则t n t x 0sin )(ω也是奇函数，而奇函数在上下限对称区间上的积分等于0。
故=n b 0。
因此，其三角函数展开式如下：其频谱如下图所示：⎪⎪⎪⎩⎪⎪⎪⎨⎧+≤≤-≤≤-+=)(202022)(00000nT t x T t t T AA t T t T A A t x 21)21(2)(12/0002/2/00000=-==⎰⎰-T T T dt t T T dt t x T a ⎰⎰-==-2/00002/2/00000cos )21(4cos )(2T T T n dt t n t T T dtt n t x T a ωω⎪⎩⎪⎨⎧==== ,6,4,20,5,3,142sin 422222n n n n n πππ⎰-=2/2/0000sin )(2T T n dtt n t x T b ω∑∞=+=1022cos 1421)(n t n nt x ωπ∑∞=++=1022)2sin(1421n t n nπωπ(n =1, 3, 5, …）（2）复指数展开式复指数与三角函数展开式之间的关系如下：)( 21=212121n 22000=-===+====nn n e n m n n n n n a barctg C R C I arctg a A b a C a A C φ A ϕ单边幅频谱 单边相频谱0 ωn φω0 3ω0 5ω0 -ω0 -3ω0 -5ω00 ωI m C nω0 3ω0 5ω0 -ω0 -3ω0 -5ω0虚频谱双边相频谱解：该三角形窗函数是一非周期函数，其时域数学描述如下：用傅里叶变换求频谱。
电子测量与仪器(第二版)习题答案
5
（2）0.2 级 10mA 量程的绝对误差为 0.2％×10mA＝0.02mA （3）0.2 级 15mA 量程的绝对误差为 0.2％×15mA＝0.03mA （4）0.1 级 100mA 量程的绝对误差为 0.1％×100mA＝0.1mA 由以上结果可知（1） ， （2） ， （3）都可以用来作为标准表，而（4）的绝对误差太大， 其中（1） ， （2）量程相同，而（3）的量程比（1） ， （2）大，在绝对误差满足要求的情况下， 应尽量选择量程接近被检定表量程，但（2） ， （3）准确度级别高，较贵，所以最适合用作 标准表的是 0.2 级 10mA 量程的。 2.14 检定某一信号源的功率输出，信号源刻度盘读数为 90μW，其允许误差为±30％，检 定时用标准功率计去测量信号源的输出功率，正好为 75μW。问此信号源是否合格? 解：信号源频率的测量绝对误差为 75μW－90μW＝－15μW 相对误差为
3
在 RI 一定时，被测电阻 RX 越大.其相对误差越小,故当 RX 相对 RI 很大时,选此方法测 量。 2.11 用一内阻为 RI 的万用表测量下图所示电路 A、 B 两点间电压， 设 E＝12V， R1＝5kΩ ， R2＝20kΩ，求： （1）如 E、R1、R2 都是标准的，不接万用表时 A、B 两点间的电压实际值 UA 为多大? （2） 如果万用表内阻 RI＝20kΩ， 则电压 UA 的示值相对误差和实际相对误差各为多大？ （3） 如果万用表内阻 RI＝lMΩ， 则电压 UA 的示值相对误差和实际相对误差各为多大？ R1 5KΩ E R2 12V 20KΩ B 解： （1）A、B 两点间的电压实际值 U A A RI V
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
电子测量原理
林占江
课后习题答案
第1章绪论
1.1 答：电子测量是以电子技术理论为依据，以电子测量仪器和设备为手段，以电量和非电量为测量对象的测量过程。
属于电子测量的是（2）、（3）。
1.2 答：见1.2节与1.3节。
1.3 答：主基准、副基准和工作基准。
第2章测量误差分析与数据处理
2.1 绝对误差：0.05V
修正值：-0.05V
实际相对误差：1.01%
示值相对误差：1.00%
电压表应定为0.5级
2.2 15V,2.5级
2.3 ±10%
2.4 绝对误差：-0.2mA；修正值：0.2mA
实际相对误差：0.25%
0.5级
2.5 14.8V,40.8%
2.6 1.15V,0.99V;23%,19.8%
2.7 5%,0.42dB
2.8 200k,266.7k,25%
2.9 200k,199.973k,0.014%
2.10 微差法、替代法、零示法
2.11 2.5级
2.12 1000.82125, 0.047
2.13 0.9926 ±0.0008
2.14 正态分布,1215.01±6.11,
2.15 86.4,
3.18, 0.00312, 5.84E4 2.16 3.3, 38
2.17 mγA+n γB, ±9.5% 2.18 ±4%
2.19 160±0.16%, 9.4±1.0%,
2.20 ±5%, ±5%
2.21 2级
第3章模拟测量方法
3.1 20%,
4.8%, 4V, 4.76
3.2 1.414, 1.11, 1; 1, 1, 1; 1.73, 1.15, 1
3.3 7.07, 10, 5.78
3.4 2格
3.5 输入已知参数的方波、三角波
3.6 不同，波形系数不同
3.7 平均值表,波形系数更接近1
3.8 见P89
3.9见P108
3.10 0.5%, 2%, 5%
3.11 27.4%, 23.1%, 20.2%
第4章数字测量方法
4.1见P115
4.2见P119
4.3见P115
4.4 4位，4位半，3位半，3位半，0.01mV 4.5 0.005%,
4.6 0.0008V, 8个字
4.7 0.000058V, 0.0032%,0.0000418,0.023%
4.8见P135
4.9见P143
4.10 0.00002%, 0.0002%, 0.002%
4.11 1.01s
4.12 100kHz
4.13 75μs
4.1见P115
4.2见P119
4.3见P115
4.4 4位，4位半，3位半，3位半，0.01mV 4.5 0.005%,
4.6 0.0008V, 8个字
4.7 0.000058V, 0.0032%,0.0000418,0.023%
4.8见P135
4.9见P143
4.10 0.00002%, 0.0002%, 0.002%
4.11 1.01s
4.12 100kHz
4.13 75μs
4.14 P144
4.15 0.05%, 20%
4.16 0.056%
4.17 100kHz, 40μs, 10
4.18 9.4ns
4.19 用外触发方式
4.20 滞后电源电压 45°
超前 45°
第5章时域测量
5.1,5.2 参阅本间相关内容
5.3 李沙育图形，是圆形。
5.4 李沙育图形（1）椭圆形（2）“8”字形5.5 被测信号频率与扫描信号频率不成整数倍，图形向左“跑动”。
5.6 被测信号频率与扫描信号频率不成整数倍，波形紊乱。
5.7 前沿有上冲，前沿弯曲。
5.8 最小周期T=0.2μs×10×10=20μs, 频率50k
5.9 最高工作频率是20MHz
5.10 最低工作频率是0.4Hz
5.11 0.02μs/cm 5.12 40ms，3ms，29ms
5.13 （1）聚焦不良（2）回扫消隐失效5.14 引入50Hz交流电源的干扰
5.15 参阅本章相关内容
第6章频域测量
6.1 P204
6.2 P205
6.3 P208
6.4 P208
6.5 P212
6.6 P214
6.7 P223
6.8 P221
6.9 P224
6.10 P223
6.11 P226
6.12 P233
第7章逻辑分析仪
7.1 P236
7.2 P237
7.3 P238
7.4 P241
7.5 P243
7.6 P246
7.7 P249
7.8 P265
8.1 P270 8.2 P272 8.3 P272 8.4 P274 8.5 P275 8.6 P276
8.7 P277
9.1 P279 9.2 P280 9.3 P281 9.4 P282 9.5 P282 9.6 P285 9.7 P286 9.8 P287
9.9 P291
10.1 P295 10.2 P297 10.3 P298 10.4 P299 10.5 P305 10.6 P308
10.7 P307
11.1 P310 11.2 P311 11.3 P314
11.4 P316
12.1 P319 12.2 P321 12.3 P325 12.4 P333 12.5 P336
12.6 P338
13.1 P339 13.2 P341 13.3 P342 13.4 P346 13.5 P347 13.6 P349。