广东省石门实验中学2019-2020学年八年级下学期第一次月考数学试题(word无答案)
广东省2019-2020学年八年级数学下学期期中测试卷一(含答案)

广东省 2019-2020学年下学期期中测试卷八年级数学一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.下列四个式子中,x的取值范围为x≥2的是( )A. B. C. D.2.一直角三角形的两直角边长为12和16,则斜边长为( )A.12 B.16 C.18 D.203.如图,在□ ABC D中,已知AD=5 cm,AB=3 cm,AE平分∠BAD交BC边于点E,则EC 等于( )A.1 cm B.2 cm C.3 cm D.4 cm4.用配方法解方程x2-4x-7=0,原方程应变形为()A. (x+2)2=11B. (x-2)2=11C.(x+4)2=23D.(x-4)2=235.如图,点P是平面坐标系中一点,则点P到原点的距离是( )A.3 B. 2 C.7 D.536.下列根式中,是最简二次根式的是( )A.0.2bB.12a-12bC.x2-y2D.5ab27.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( ) A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形8.已知菱形ABC D中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )A.16 3 B.16 C.8 3 D.89.如图,在四边形ABC D中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD 的面积为8,则BE=( )A.2 B.3 C.2 2 D.2 310.如图所示,A(-3,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )A.74B. 2C. 3 D.2二、填空题(本大题共7小题,每小题4分,共28分)11.已知(x-y+3)2+2-y=0,则x+y=________.12.已知最简二次根式4a+3b与可以合并,则ab=________.13.下面四组数:①4,5,6;②6,8,10;③8,15,17;④9,40,41,其中有一组与其他三组规律不同的是________.14.如图,已知△AB C中,AB=5 cm,BC=12 cm,AC=13 cm,那么AC边上的中线BD的长为________cm.15.如图,在矩形ABC D中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的点F上,则DF的长为________.16.如图,已知在Rt△AB C中,∠ACB=90°,AB=4,分别以AC、BC为直径作半圆,面积分别记为S1、S2,则S1+S2等于________.17.如图所示,直线a经过正方形ABCD的顶点A,分别过顶点B、D作DE⊥a于点E、BF⊥a 于点F,若DE=4,BF=3,则EF的长为________.三、解答题(本大题共8小题,共62分.解答应写出文字说明、证明过程或演算步骤) 18.(6分)计算: (1) 212+3113-513-2348; (2)48-54÷2+(3-3)(1+13).19.(6分)已知x 、y 为实数,且y +1,求(-y )x的值20.(6分)在解答“判断由长为65、2、85的线段组成的三角形是不是直角三角形”一题中,小明是这样做的:解:设a =65,b =2,c =85.又因为a 2+b 2=(65)2+22=13625≠6425=c 2,所以由a 、b 、c 组成的三角形不是直角三角形,你认为小明的解答正确吗?请说明理由.21.(8分)如图,铁路上A、B两点相距25 km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在离A站多少km处?22.(8分)如图,E、F、G、H分别是边AB、BC、CD、DA的中点.(1)判断四边形EFGH的形状,并证明你的结论;(2)当BD、AC满足什么条件时,四边形EFGH是正方形.(不要求证明)23.(8分)如图,四边形ABCD是一个菱形绿地,其周长为40 2 m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2,请问需投资金多少元?(结果保留整数)24.(10分)如图,在平行四边形ABC D中,E为BC的中点,连接AE并延长交DC的延长线于点F.(1)求证:AB=CF;(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.25.(10分)如图,在Rt△AB C中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(1)求证:AE=DF;(2) 四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;(3)当t为何值时,△DEF为直角三角形?请说明理由.广东省2019-2020学年八年级数学下学期期中测试卷(解析版)一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.下列四个式子中,x的取值范围为x≥2的是( )A. B. C. D.【答案】C【解析】A、x-2≥0,且x-2≠0,解得:x>2,故此选项错误;B、x-2>0,解得:x>2,故此选项错误;C、x-2≥0,解得x≥2,故此选项正确;D、2-x≥0,解得x≤2,故此选项错误;2.一直角三角形的两直角边长为12和16,则斜边长为( )A.12 B.16 C.18 D.20【答案】D【解析】因为知道两个直角边长,根据勾股定理可求出斜边长.∵三角形的两直角边长为12和16,∴斜边长为:162+122=20.故选D3.如图,在□ ABC D中,已知AD=5 cm,AB=3 cm,AE平分∠BAD交BC边于点E,则EC 等于( )A.1 cm B.2 cm C.3 cm D.4 cm【答案】B【解析】本题难度中等,考查平行四边形中的计算.根据平行四边形的性质,可得AD∥BC,AD=BC=5,再根据AE平分∠BAD,可得△ABE是等腰三角形,BE=AB=3.所以EC=BC-BE =5-3=2,答案选择B.一般情况下,在几何图形中有平行线和角平分线就会得出等腰三角形.4.用配方法解方程x2-4x-7=0,原方程应变形为()A. (x+2)2=11B. (x-2)2=11C.(x+4)2=23D.(x-4)2=23【答案】B【解析】解:x2-4x=7,x2-4x+4=11,所以(x-2)2=11.故选B.5.如图,点P是平面坐标系中一点,则点P到原点的距离是( ) A.3 B. 2 C.7 D.53【答案】A【解析】连接PO,∵点P的坐标是(,),∴点P到原点的距离= =3故选A.6.下列根式中,是最简二次根式的是( )A.0.2bB.12a-12bC.x2-y2D.5ab2【答案】C【解析】因为:A、 =;B、 =2D、 = |b|;所以这三项都可化简,不是最简二次根式.故选C.7.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( ) A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形【答案】D【解析】A:正确,一组邻边相等的平行四边形是菱形;B:正确,对角线互相垂直的平行四边形是菱形;C:正确,有一专个角为90°的平行四边形是矩形;D:不正确,对角线相等的平行四边形是矩形而不属是正方形;故选D.8.已知菱形ABC D中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )A.16 3 B.16 C.8 3 D.8【答案】C【解析】∵四边形ABCD是菱形,∴AC⊥BD,OA=OC=AC= ×4=2,∠BAC= ∠BAD= ×120°=60°,∴AC=4,∠AOB=90°,∴∠ABO=30°,∴AB=2,OA=4,OB=2,∴BD=2OB=4,∴该菱形的面积是:AC•BD=×4×4 =8,故选C.9.如图,在四边形ABC D中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD 的面积为8,则BE=( )A.2 B.3 C.2 2 D.2 3【答案】C【解析】解:过B点作BF⊥CD,与DC的延长线交于F点,∵∠FBC+∠CBE=90°,∠ABE+∠EBC=90°,∴∠FBC=∠ABE,在△BCF和△BE A中∴△BCF≌△BEA(AAS),则BE=BF,S四边形ABCD=S正方形BEDF=8,∴BE==2.故答案为2.10.如图所示,A(-3,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )A.74B. 2C. 3 D.2【答案】C【解析】解:过P点作PD⊥x轴,垂足为D,由A(-,0)、B(0,1),得OA=,OB=1,∵△ABC为等边三角形,由勾股定理,得AB==2,∴S△ABC=×2×=,又∵S△ABP=S△AOB+S梯形BODP-S△ADP=××1+ ×(1+a)×3- ×(+3)×a= ,由2S△ABP=S△ABC,得 +3- a=,∴a=.故选C.二、填空题(本大题共7小题,每小题4分,共28分)11.已知(x-y+3)2+2-y=0,则x+y=________.【答案】1【解析】∵(x-y+3)2+ =0,∴x-y+3=02-y=0 ,解得x=-1y=2 ,则x+y=-1+2=1,故答案为1.12.已知最简二次根式4a+3b与可以合并,则ab=________.【答案】1【解析】∵最简二次根式与可是同类二次根式,∴b+1=2 , 4a+3b=2a-b+6 ,解得:a=1,b=1,故=1.13.下面四组数:①4,5,6;②6,8,10;③8,15,17;④9,40,41,其中有一组与其他三组规律不同的是________.【答案】③【解析】第三组.因为第三组无法构成三角形14.如图,已知△AB C中,AB=5 cm,BC=12 cm,AC=13 cm,那么AC边上的中线BD的长为________cm.【答案】【解析】∵AB=5cm,BC=12cm,AC=13cm,由勾股定理的逆定理得,△ABC是直角三角形,∴BD= AC= cm.15.如图,在矩形ABC D中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的点F上,则DF的长为________.【答案】6【解析】解:∵四边形ABCD是矩形,∴AB=DC=8,∠D=90°,∵将矩形ABCD沿CE折叠后,点B落在AD边的F点上,∴CF=BC=10,在Rt△CDF中,由勾股定理得:DF= = =617.如图,已知在Rt△AB C中,∠ACB=90°,AB=4,分别以AC、BC为直径作半圆,面积分别记为S1、S2,则S1+S2等于________.【答案】2π【解析】S1= πAC2,S2= πBC2,所以S1+S2= π(AC2+BC2)= πAB2=2π.故答案为:2π.17.如图所示,直线a经过正方形ABCD的顶点A,分别过顶点B、D作DE⊥a于点E、BF⊥a 于点F,若DE=4,BF=3,则EF的长为________.【答案】7【解析】解:∵ABCD 是正方形 ∴AB =AD ,∠B =∠A =90° ∵∠B +∠ABF =∠A +∠DAE ∴∠ABF =∠DAE在△权AFB 和△AE D 中,∠ABF =∠DAE ,∠AFB =∠AED ,AB =AD ∴△AFB ≌△AED ∴AF =DE =4,BF =AE =3 ∴EF =AF +AE =4+3=7.三、解答题(本大题共8小题,共62分.解答应写出文字说明、证明过程或演算步骤) 18.(6分)计算: (1) 212+3113-513-2348; (2)48-54÷2+(3-3)(1+13). 【解析】(1)原式=4+2 -- =2 (2)原式= 4-+(1-)=4- -219.(6分)已知x 、y 为实数,且y 2014x -2014x - +1,求(-y )x的值【解析】x -2014≥0,2014-x ≥0; 解得:x =2014y =1(-y ) x = (-1)2014=120.(6分)在解答“判断由长为65、2、85的线段组成的三角形是不是直角三角形”一题中,小明是这样做的:解:设a =65,b =2,c =85.又因为a 2+b 2=(65)2+22=13625≠6425=c 2, 所以由a 、b 、c 组成的三角形不是直角三角形,你认为小明的解答正确吗?请说明理由.【解析】设a =,b =2,c =.∵a 2+b 2=()2+22 =,c 2=()2 = ,∴a 2+b 2≠c 2,∴这三条线段组成的三角形不是直角三角形.21.(8分)如图,铁路上A 、B 两点相距25 km ,C 、D 为两村庄,DA ⊥AB 于A ,CB ⊥AB 于B ,已知DA =15 km ,CB =10 km ,现在要在铁路AB 上建一个土特产品收购站E ,使得C 、D 两村到E 站的距离相等,则E 站应建在离A 站多少km 处?【解析】解:∵使得C ,D 两村到E 站的距离相等.∴DE =CE ,∵ DA ⊥AB 于A ,CB ⊥AB 于B ,∴∠A =∠B =90°,∴=,=∴=,设AE=x,则BE=AB-AE=(25-x),∵DA=15km,CB=10km,∴x2+152=(25-x)2+102,解得:x=10,∴AE=10km;22.(8分)如图,E、F、G、H分别是边AB、BC、CD、DA的中点.(1)判断四边形EFGH的形状,并证明你的结论;(2)当BD、AC满足什么条件时,四边形EFGH是正方形.(不要求证明) 【解析】(1)在△AB C中,E、F分别是边AB、B C中点,所以EF∥AC,且EF=AC,同理有GH∥AC,且GH=AC,∴EF∥GH且EF=GH,故四边形EFGH是平行四边形.(2)EH∥BD且EH= BD,若AC=BD,则有EH=EF,又因为四边形EFGH是平行四边形,∴四边形EFGH是菱形,∵AC⊥BD,∴∠EHG=90°,即:当AC=BD且AC⊥BD时,四边形EFGH是正方形.23.(8分)如图,四边形ABCD是一个菱形绿地,其周长为40 2 m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2,请问需投资金多少元?(结果保留整数)【解析】连接BD,AC,∵菱形ABCD的周长为40m,∴菱形ABCD的边长为10m,∵∠ABC=120°,∴△ABD,△BCD是等边三角形,∴对角线BD=10m,AC=10m,∵E,F,G,H是菱形ABCD各边的中点,∴四边形EFGH是矩形,矩形的边长分别为5m,5m,∴矩形EFGH的面积为5×5=50(m2),即需投资金为50×10=500≈866(元).答:需投资金为866元.24.(10分)如图,在平行四边形ABC D中,E为BC的中点,连接AE并延长交DC的延长线于点F.(1)求证:AB=CF;(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.【解析】证明:(1)∵四边形ABCD是平行四边形,∴AB∥CD,∵点F为DC的延长线上的一点,∴AB∥DF,∴∠BAE=∠CFE,∠ECF=∠EBA,∵E为B C中点,∴BE=CE,则在△BAE和△CFE中,∠BAE=∠CFE∠ECF=∠EBABE=CE∴△BAE≌△CFE,∴AB=CF.(2)当BC=AF时,四边形ABFC是矩形.理由如下:∵AB∥CF,AB=CF,∴四边形ABFC是平行四边形,∵BC=AF,∴四边形ABFC是矩形.25.(10分)如图,在Rt△AB C中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(1)求证:AE=DF;(2) 四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;(3)当t为何值时,△DEF为直角三角形?请说明理由.【解析】证明:(1)∵在Rt△AB C中,∠B=90°,AC=60cm,∠A=60°,∴∠C=90°-∠A=30°.∵CD=4t cm,AE=2t cm,又∵在直角CDF中,∠C=30°,∴DF=CD=2t cm,∴DF=AE;(2)能,∵DF∥AB,DF=AE,∴四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,即60-4t=2t,解得:t=10,即当t=10时,□AEFD是菱形(3)①当∠DEF=90°时,由(1)知四边形AEFD为平行四边形,∴EF∥AD,∴∠ADE=∠DEF=90°,∵∠A=60°,∴∠AED=30°,∴AD=AE=t,又AD=60-4t,即60-4t=t,解得t=12;②当∠EDF=90°时,四边形EBFD为矩形,在Rt△AE D中∠A=60°,则∠ADE=30°,∴AD=2AE,即60-4t=4t,解得t=;③若∠EFD=90°,则E与B重合,D与A重合,此种情况不存在.综上所述,当t=s或12s时,△DEF为直角三角形。
广东省2020年八年级下第一次段考数学月考试卷
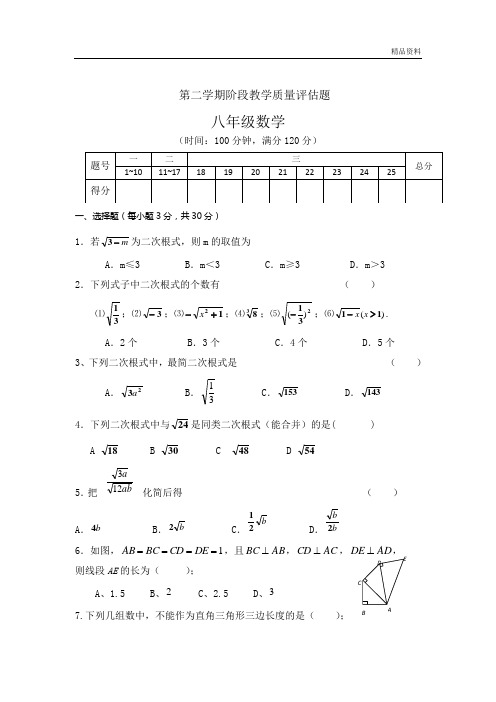
第二学期阶段教学质量评估题八年级数学(时间:100分钟,满分120分)一、选择题(每小题3分,共30分)1.若m -3为二次根式,则m 的取值为A .m ≤3B .m <3C .m ≥3D .m >3 2.下列式子中二次根式的个数有 ( ) ⑴31;⑵3-;⑶12+-x ;⑷38;⑸231)(-;⑹)(11>-x x .A .2个B .3个C .4个D .5个 3、下列二次根式中,最简二次根式是 ( )A .23aB .31C .153D .143 4.下列二次根式中与24是同类二次根式(能合并)的是( ) A 18 B 30 C 48 D 54 5.把化简后得 ( )A .b 4B .b 2C .b21 D .b b 26.如图,1====DE CD BC AB ,且AB BC ⊥,AC CD ⊥,AD DE ⊥,则线段AE 的长为( );A 、1.5B 、2C 、2.5D 、37.下列几组数中,不能作为直角三角形三边长度的是( );aba123ABCDEA、1.5,2,2.5B、3,4,5C、5,12,13D、20,30,408、已知直角三角形两边的长为3和4,则此三角形的周长为().A.12 B.7+7C.12或7+7D.以上都不对9、三角形的三边长a,b,c满足()222ab a b c=+-则此三角形是 ().A、钝角三角形B、锐角三角形C、直角三角形D、等边三角形10、n 的值是()A.0 B.1 C.2 D.5二、填空题(每小题4分,共11.化简12.计算:2)82(⨯+13.最简二次根式b a a-+12与3+a可以合并,则a+b=14. 在直角三角形ABC中,∠C = 90°,BC = 12,AC = 9,则AB=.15.如上图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为___________cm2.16.写出命题“同位角相等,两直线平行”的逆命题是。
2019-2020年八年级数学下学期第一次月考试题及答案

2019-2020年八年级数学下学期第一次月考试题及答案
说明:本答案仅供参考,若考生答案与本答案不一致,只要正确,同样得分.
参考答案:
三、19.解:(1)小莉所调查的样本缺乏代表性;
(2)会在每包的每打中随机抽取一套当做样本.(答案不唯一,正确即可)
20.解:如图.
21.解:(1)如图;点B的坐标为(-1,1),点C的坐标为
(-4,0),点E的坐标为(0,-4),点F的坐标为(1,
-1),点G的坐标为(4,0),点H的坐标为(1,1);
(2)点A与点E,点B与点D,点H与点F.
22.解:(1)2014年5月到12月该市共有122天的空气质
量达到良好以上;
圆心角的度数为225°,C部分扇形的圆心角的度数为
90°.
23.解:(1)八年级(2)班共有50名学生;
(2)B所在扇形的圆心角的度数为72°;如图;
(3)这顿午饭八年级(2)班的学生浪费了150克米饭.
24.解:(1)数据中的最大值和最小值各为4.1和2.2;
(2)如图;如图;
(3)台湾该医院8月份出生的32名新生婴儿中,正常
体重儿占总新生婴儿的78.125%,低体重儿占总新生
婴儿的9.375%,巨大儿占总新生婴儿的12.5%.。
实验中学2019-2020学年八年级(下)第一次月考数学试卷(含答案解析)

实验中学2019-2020学年八年级(下)第一次月考数学试卷一、选择题(本大题共10小题,共30.0分)1. 不等式3x ≤2(x −1)的解集为( )A. x ≤−1B. x ≥−1C. x ≤−2D. x ≥−22. 如图,在△ABC 中,AB =AC ,点D 在BC 上,且AD =BD ,∠1=30°,则∠DAC 的度数为( )A. 80°B. 90°C. 100°D. 110°3. 不等式组{x +2≥12(x +3)−3≥3x的解集在数轴上表示正确的是( ) A.B. C. D.4. 角的平分线是到角两边距离相等的点的集合。
( )A. 正确B. 错误5. 已知a >b ,则下列不等式的变形不正确的是( )A. a −8>b −8B. 7a >7bC. −4a >−4bD. a 3>b3 6. 两个锐角分别相等的两个直角三角形( )全等.A. 不一定B. 一定不C. 一定D. 以上都不对7. 某次知识竞赛共有30道题,每一题答对得5分,答错或不答都扣3分,小亮得分要超过70分,他至少要答对多少道题?如果设小亮答对了x 道题,根据题意列式得( )A. 5x −3(30−x)>70B. 5x +3(30−x)≤70C. 5x −3(30+x)≥70D. 5x +3(30−x)>708. 如图,在△ABC 中,D 在BC 上,若AD =BD ,AB =AC =CD ,则∠ABC的度数是( )A. 30°B. 35°C. 36°D. 60°9.已知点(−2,y1),(1,0),(3,y2)都在一次函数y=kx−2的图象上,则y1,y2,0的大小关系是()A. 0<y1<y2B. y1<0<y2C. y1<y2<0D. y2<0<y110.如图,已知△ABC是等腰三角形,AC=BC=5,AB=8,D为底边AB上的一个动点(不与A、B重合),DE⊥AC,DF⊥BC,垂足分别为E、F,则DE+DF的值为()A. 3B. 4C. 185D. 245二、填空题(本大题共5小题,共15.0分)11.不等式12x−5≤1−32x的正整数解是______ .12.已知等腰三角形一边的长是4cm,另一边的长是7cm,则这个三角形的周长是____________;13.解不等式15−3x2≥7−x,并把它的解集在数轴上表示出来.以下是小明的解答过程:解:第一步去分母,得15−3x≥2(7−x),第二步去括号,得15−3x≥14−2x,第三步移项,得−3x+2x≥14−15,第四步合并同类项,得−x≥−1,第五步系数化为1,得x≥1.第六步把它的解集在数轴上表示为:请指出小明从第几步开始出现了错误,并说明判断依据.答:__________________________________________________________________.14.如图,在△ABC中,AD垂直平分BC,交BC于点E,CD⊥AC,若AB=6,CD=3,则BE=_______.15.如图,平面直角坐标系中,△OPQ为等腰三角形,点Q位于x轴上,则满足条件点Q的有_____个.三、解答题(本大题共8小题,共64.0分)16.解不等式,并在数轴上表示解集.17.解不等式组{x−3>1−7x1+4x≥5x−2,并在数轴上将解集表示出来18.如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,(1)请画出平移后的图形△A′B′C′(2)并写出△A′B′C′各顶点的坐标.19.如图,E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD交OE于点F,若∠AOB=60°.(1)求证:△OCD是等边三角形;(2)若EF=5,求线段OE的长.20.已知关于x的不等式4x+a3>1的解都是不等式2x+13>0的解,求a的取值范围.21.如图,△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE//AC,交AB于E,若AB=6,求线段DE的长.22.学校准备购进一批篮球和足球,买1个篮球和2个足球共需170元,买2个篮球和1个足球共需190元.(1)求一个篮球和一个足球的售价各是多少元?(2)学校欲购进篮球和足球共100个,且足球数量不多于篮球数量的2倍,求出最多购买足球多少个?23.如图,在平面直角坐标系中,矩形OABC的顶点A在y轴上,顶点C在x轴上,顶点B的坐标为(8,4).直线y=−35x+295与矩形OABC的边AB,BC分别交于点D、点E,连接OD、OE.(1)求点D和点E的坐标.(2)求△ODE的面积.(3)点P在线段OA上,且不与点O和点A重合,点Q(m,0)在x轴上,是否存在m的值使∠OQP=∠DPA?若存在,请直接写出m的取值范围;若不存在,请说明理由.【答案与解析】1.答案:C解析:解:去括号得,3x ≤2x −2,移项、合并同类项得,x ≤−2,故选:C .根据解一元一次不等式的步骤:去括号、移项、合并同类项计算,即可得到答案.本题考查的是一元一次不等式的解法,掌握解一元一次不等式的一般步骤是解题的关键. 2.答案:B解析:本题考查了等腰三角形的性质,三角形的内角和定理,属于基础题.根据等边对等角可得∠B =∠1,∠B =∠C ,再根据三角形的内角和等于180°列式计算即可得解. 解:∵AD =BD ,∴∠B =∠1=30°,∵AB =AC ,∴∠B =∠C =30°,在△ABC 中,∠DAC =180°−30°×3=90°.故选B .3.答案:B解析:解:{x +2≥1…①2(x +3)−3≥3x …②, 解①得x ≥−1,解②得x ≤3.则表示为:故选B .首先解每个不等式,然后把每个不等式的解集在数轴上表示即可.本题考查了不等式组的解法以及用数轴表示不等式的解集,要注意“两定”:一是定界点,一般在数轴上只标出原点和界点即可.定边界点时要注意,点是实心还是空心,若边界点含于解集为实心点,不含于解集即为空心点;二是定方向,定方向的原则是:“小于向左,大于向右”.4.答案:A解析:本题考查了角平分线的性质,即到角的两边距离相等的点在角的平分线上.解:由角平分线的性质即到角的两边距离相等的点在角的平分线上,故选A.5.答案:C解析:此题考查了不等式的性质,熟练掌握不等式的性质是解本题的关键.根据不等式的性质:不等式左右两边都加上或减去同一个数或整式,不等号方向不变;不等式左右两边都乘以或除以同一个正数,不等号方向不变;不等式左右两边都乘以或除以同一个负数,不等号方向改变,即可做出判断.解:A.∵a>b,∴a−8>b−8,本选项不合题意;B.∵a>b,∴7a>7b,本选项不合题意;C.∵a>b,∴−4a<−4b,本选项符合题意;D.∵a>b,∴a3>b3,本选项不合题意,故选C.6.答案:A解析:解:由三个角分别相等的两个三角形不一定全等,得两个锐角分别相等的两个直角三角形不一定全等,故选:A.根据全等三角形的判定,可得答案.本题考查了直角三角形全等的判定,熟记三角形的判定定理是解题关键.7.答案:A解析:解:根据题意,得5x−3(30−x)>70.故选:A.小明答对题的得分:5x;小明答错题的得分:−3(30−x).不等关系:小明得分要超过70分.此题主要考查了由实际问题抽象出一元一次不等式,抓住关键词语,找到不等关系是解题的关键.8.答案:C解析:解:∵AB=AC,∴∠B=∠C,∵AD=BD,∴∠B=∠DAB,∵AC=CD,∴∠DAC=∠ADC=2∠B=2∠C,又∵∠C+∠ADC+∠DAC=180°,∴∠B+2∠B+2∠B=180°∴5∠B=180°,∴∠B=36°,故选:C.AB=AC可得∠B=∠C,AD=BD可得∠B=DAB,由AC=CD,可得∠ADC=∠DAC=2∠B,在△ACD 中利用三角形内角和定理可求出∠B.本题主要考查等腰三角形的性质,掌握等边对等角是解题的关键,注意三角形内角和定理和方程思想的应用.9.答案:B解析:本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.也考查了一次函数的性质.先根据点(1,0)在一次函数y=kx−2的图象上,求出k=2>0,再利用一次函数的性质判断出函数的增减性,然后根据三点横坐标的大小得出结论.解:∵点(1,0)在一次函数y=kx−2的图象上,∴k−2=0,∴k=2>0,∴y随x的增大而增大,∵−2<1<3,∴y1<0<y2.故选:B.10.答案:D解析:本题考查的是等腰三角形的性质、勾股定理及三角形的面积,熟知等腰三角形三线合一的性质是解答此题的关键.连接CD,过点C作CE⊥AB于点E,根据勾股定理求出CE的长,再由三角形的面积公式即可得出结论.解:连接CD,过点C作CE⊥AB于点E,如图,∵AC=BC=5,AB=8,∴AE=4,∴CE=√52−42=3,∴S△ABC=12AB⋅CE=12×8×3=12.∵DE⊥AC,DF⊥BC,∴S△ABC=S△ACD+S△BDC=12AC⋅DE+12BC⋅DF=12×5×(DE+DF)=12,∴DE+DF=245.故选D.11.答案:1,2,3解析:解:移项,得:12x+32x≤1+5,合并同类项,得:2x≤6,系数化成1得:x≤3.则正整数解是:1,2,3.故答案是:1,2,3.首先移项、合并同类项、系数化成1,求得不等式的解集,然后确定正整数解即可.本题考查了一元一次不等式的解法,正确解不等式,求出解集是解答本题的关键.解不等式应根据不等式的基本性质.12.答案:15cm或18cm解析:本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.题目给出等腰三角形有两条边长为4cm和7cm,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.解:①当腰长为4cm时,等腰三角形三边长为4cm、4cm、7cm,符合三角形三边关系,则三角形的周长为:4+4+7=15cm;②当腰长为7cm时,等腰三角形三边长为4cm、7cm、7cm,符合三角形三边关系,则三角形的周长为:4+7+7=18cm.因此这个三角形的周长为15或18cm.故填15cm或18cm.13.答案:第五步,不等式两边同除以一个负数,不等号方向应改变解析:本题考查解一元一次不等式,以及在数轴上表示不等式的解集,正确根据不等式的性质求解是解题关键.注意去分母和系数化为1时不等号的变化即可得解.解:根据题意可得系数化为1时,不等式两边同除以−1,则不等号方向改变,∴第五步出现了错误.故答案为第五步,不等式两边同除以一个负数,不等号方向应改变.14.答案:65√5解析:本题考查了勾股定理、线段垂直平分线的性质等知识;熟练掌握勾股定理和线段垂直平分线的性质是解题的关键.由线段垂直平分线的性质得出AC=AB=6,由勾股定理求出AD,再由三角形面积即可得出答案.解:∵AD垂直平分BC,∴AC=AB=6,BE=CE,∵CD⊥AC,∴AD=√AC2+CD2=3√5∵△ACD的面积=12AD·CE=12AC·CD∴CE=AC·CDAD =6√55,∴BE=65√5.故答案为65√5.15.答案:4解析:本题考查等腰三角形的判定和点的坐标的确定,根据等腰三角形的定义,可知有四种情况,先求出OP是关键.解:如图,∵点P(X,Y),∴OP=√x2+y2,,①OP 是底边时,点Q 1的坐标为(x,0);②OP 是腰时,点Q 2的坐标为(√x 2+y 2,0)或Q 4(−√x 2+y 2,0)或Q 3(2x,0);综上所述,满足条件的Q 坐标为(x,0),(√x 2+y 2,0),(−√x 2+y 2,0)和(2x,0).故答案为4.16.答案:解:,4x −1−3x >3,4x −3x >3+1,x >4,将不等式的解集表示在数轴上如下:解析:本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.根据解一元一次不等式基本步骤:去分母、移项、合并同类项可得.17.答案:解:{x −3>1−7x①1+4x ⩾5x −2②由①得:8x >4x >0.5由②得:x ≤3则不等式的解集为0.5<x ≤3,在数轴上表示如下:解析:本题考查了解一元一次不等式组以及在数轴上表示不等式的解集,解题的关键是求出不等式组的解集.分别解不等式①②,由此即可得出不等式组的解集,再将其在数轴上表示出来即可.18.答案:解:(1)如图,△A′B′C′即为所求;;(2)由图可知,A′(4,0),B′(1,3),C′(2,−2).解析:本题考查的是作图−平移变换,熟知图形平移的性质是解答此题的关键.(1)根据图形平移的性质画出△A′B′C′;(2)根据图像写出△A′B′C′各顶点的坐标.19.答案:解:(1)∵点E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,垂足分别是C,D,∴DE=CE,在Rt△ODE与Rt△OCE中,{DE=CEOE=OE,∴Rt△ODE≌Rt△OCE(HL),∴OD=OC,∵∠AOB=60°,∴△OCD是等边三角形;(2)∵△OCD是等边三角形,OF是∠COD的平分线,∴OE⊥DC,∵∠AOB=60°,∴∠AOE=∠BOE=30°,∵∠ODF=60°,ED⊥OA,∴∠EDF=30°,∴DE=2EF=10,∴OE=2DE=20.解析:本题考查了等边三角形的判定和性质,角平分线的性质,三角形全等的判定和性质,30°的直角三角形的性质等,熟练掌握性质和定理是解题的关键.(1)根据角平分线的性质得出DE=CE,然后根据HL证得Rt△ODE≌Rt△OCE,得出OD=OC,由∠AOB=60°,证得△OCD是等边三角形;(2)根据三线合一的性质得出∠AOE=∠BOE=30°,OE⊥DC,进而证得∠EDF=30°,然后根据30°的直角三角形的性质即可求得OE的长.20.答案:解:由4x+a3>1,得:x>3−a4,由2x+13>0,得:x>−12,∵关于x的不等式4x+a3>1的解都是不等式2x+13>0的解,∴3−a4≥−12,解得a≤ 5.答:a的取值范围是a≤ 5.解析:本题考查了解一元一次不等式,分别求出两个不等式的解集,再根据同大取大列出关于a的不等式是解题的关键.先把a看作常数求出两个不等式的解集,再根据同大取大列出不等式求解即可.21.答案:解:∵AD 平分∠BAC ,∴∠EAD =∠CAD ,∵DE//AC ,∴∠EDA =∠CAD ,∴∠EAD =∠EDA ,∴AE =DE ,∵BD ⊥AD ,∴∠EBD +∠EAD =∠BDE +∠EDA =90°,∴∠EBD =∠BDE ,∴DE =BE ,∴DE =12AB =3.解析:本题考查了角平分线的定义,平行线的性质,等腰三角形的判定与性质及直角三角形的性质,解决本题的关键是证明出AE =DE .根据角平分线的定义可得∠EAD =∠CAD ,根据平行线的性质可得∠EDA =∠CAD ,得到∠EAD =∠EDA ,进而得到AE =DE ,再根据等角的余角相等得到∠EBD =∠BDE ,从而得到DE =BE ,即可得到结论.22.答案:解:(1)设一个篮球和一个足球的售价各是x 元、y 元,{x +2y =1702x +y =190,得{x =70y =50, 答:一个篮球和一个足球的售价各是70元、50元;(2)设购进足球a 个,a ≤2(100−a),解得,a ≤6623,∴最多购买足球66个,答:最多购买足球66个.解析:(1)根据题意可以列出相应的二元一次方程组,从而可以解答本题;(2)根据题意可以列出相应的不等式,从而可以解答本题.本题考查一元一次不等式的应用、二元一次方程组的应用,解答本题的关键是明确题意,列出相应的方程组和不等式,利用方程的思想和不等式的性质解答.23.答案:解:(1)直线y=−35x+295,当y=4时,4=−35x+295,解得:x=3,故点D的坐标为(3,4),同理可得点E的坐标为(8,1);(2)S△ODE=S矩形ABCO −S△OEC−S△BDE−S△AOD=4×8−12×4×3−12×8×1−12×3×5=292;(3)存在,理由:设OP=a,则:AP=4−a,OQ=m,AD=3,∵∠OQP=∠DPA,∴tan∠OQP=tan∠DPA,a 3=m4−a,m=−13a2+43a,当a=2时,m取得最大值为43,故:m的取值范围为:0<m≤43.解析:本题为一次函数综合题,考查了解直角三角形、面积的计算方法、二次函数的基本性质等,其中(3),利用二次函数性质求m的取值范围是本题的难点.(1)直线y=−35x+295,当y=4时,4=−35x+295,即可求解;(2)S△ODE=S矩形ABCO−S△OEC−S△BDE−S△AOD,即可求解;(3)∠OQP=∠DPA,则tan∠OQP=tan∠DPA,则m=−13a2+43a,利用二次函数性质即可求解.。
广东省2020年八年级下学期第一次月考数学试题 (2)

初中部第一次月考 八年级 数学科试卷 共 4 页 1 13{x x ≥≤广东省 八年级下学期第一次月考数学试题一. 选择题(每小题3分,共36分)题 号 1 2 3 4 5 6 7 8 9 10 11 12 答 案1.以下各组数为三角形的三条边长,其中能作成直角三角形的是 ( )A .2,3,4B .4,5,6C .2,3,5D .2,2,4 2.下列各式从左到右的变形中,是因式分解的是( )A 、()()2339a a a +-=-B 、()()22a b a b a b -=+-C 、()24545a a a a --=--D 、23232m m m m m ⎛⎫--=-- ⎪⎝⎭3.下列条件中能判定△ABC ≌△DEF 的是 ( )A .AB =DE ,BC =EF ,∠A =∠D B .∠A =∠D ,∠B =∠E ,∠C =∠F C .AC =DF ,∠B =∠F ,AB =DE D .∠B =∠E ,∠C =∠F ,AC =DF 4.下列命题中正确的是 ( )A .有两条边相等的两个等腰三角形全等B .两腰对应相等的两个等腰三角形全等C .两角对应相等的两个等腰三角形全等D .一边对应相等的两个等边三角形全等5.至少有两边相等的三角形是( )A .等边三角形B .等腰三角形C .等腰直角三角形D .锐角三角形6.函数y =kx +b (k 、b 为常数,k ≠0)的图象如图所示, 则关于x 的不等式kx +b >0的解集为( ).A .x >0B .x <0C .x <2D .x >27.已知x y >,则下列不等式不成立的是 ( ).A .66x y ->-B .33x y >C .22x y -<-D .3636x y -+>-+8.将不等式组 的解集在数轴上表示出来,应是( ).A9.下列各式分解因式错误的是( )A CBD10.如果不等式组⎩⎨⎧>-<+mx x x 148的解集是3>x ,那么m 的取值范围是( )A .3≥mB .3≤mC .3=mD .3<m11.已知,如图,在△ABC 中,OB 和OC 分别平分∠ABC 和∠ACB ,过O 作DE ∥BC ,分别交AB 、AC 于点D 、E ,若BD +CE =5,则线段DE 的长为 ( )A .5B .6C .7D .812.若多项式()281nx -能分解成()()()2492323x x x ++-,那么n =( )A 、2B 、4C 、6D 、8 二、填空题(每小题3分,共12分)13.等腰三角形的一个角为45°,则顶角是 . 14.不等式930x ->的非负整数解是 . 15.若5,6x y xy -==则22x y xy -=_________。
广东省南海区石门实验中学2019-2020学年中考数学模拟检测试题

广东省南海区石门实验中学2019-2020学年中考数学模拟检测试题一、选择题1.如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B (﹣1,0),则①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣1<x<3,其中正确的个数是()A.1B.2C.3D.42.如图,已知直线y=334x ,与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB,则△PAB面积的最小值是()A.6B.5.5C.5D.4.53.不透明布袋中装有除颜色外没有其他区别的1个红球和2个白球,搅匀后从中摸出一个球,放回搅匀,再摸出第二个球,两次都摸出白球的概率是()A.29B.13C.49D.594.如图,是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是()A.矩形B.菱形C.正方形D.无法确定5.如图,在等腰直角三角形ABC 中,AB =AC =2,∠BAC =90°,点D 是AC 的中点,点P 是BC 边上的动点,连接PA 、PD .则PA+PD 的最小值为( )1 D.36.如图,,,AB AC BD 是O 的切线,切点分别是,,P C D .若5,3AC BD ==,则AB 的长是( )A .2B .4C .6D .8 7.已知|a|=3,b 2=16,且|a+b|≠a+b,则代数式a ﹣b 的值为( ) A .1或7B .1或﹣7C .﹣1或﹣7D .±1或±7 8.如图,点I 和O 分别是△ABC 的内心和外心,则∠AIB 和∠AOB 的关系为( )A.∠AIB =∠AOBB.∠AIB≠∠AOBC.2∠AIB ﹣12∠AOB =180°D.2∠AOB ﹣12∠AIB =180° 9.如图,平行四边形ABCD 中,对角线AC 、BD 相交于O ,BD=2AD ,E 、F 、G 分别是OC 、OD 、AB 的中点,下列结论:①BE ⊥AC ;②EG=GF ;③△EFG ≌△GBE ;④EA 平分∠GEF ;⑤四边形BEFG 是菱形.其中正确的是( )A .①②③B .①③④C .①②⑤D .②③⑤10.二次函数y =ax 2﹣4ax+2(a≠0)的图象与y 轴交于点A ,且过点B (3,6)若点B 关于二次函数对称轴的对称点为点C ,那么tan ∠CBA 的值是( )A .23B .43C .2D .3411.已知边长为4的等边△ABC ,D 、E 、F 分别为边AB 、BC 、AC 的中点,P 为线段DE 上一动点,则PF+PC 的最小值为( )A .4B .C .D .212.某机构调查了某小区部分居民当天行走的步数(单位:千步),并将数据整理绘制成如下不完整的频数直方图和扇形统计图.根据统计图,得出下面四个结论:①此次一共调查了200位小区居民;②行走步数为8~12千步的人数超过调查总人数的一半;③行走步数为4~8千步的人数为50人;④扇形图中,表示行走步数为12~16千步的扇形圆心角是72°.其中正确的结论有( )A .①②③B .①②④C .②③④D .①③④ 二、填空题13.已知反比例函数的图像经过点,A B ,点A 的坐标为(1,3),点B 的纵坐标为1,则点B 的横坐标为__________.14.为了了解一批圆珠笔芯的使用寿命,宜采用________方式进行调查;为了了解某班同学的身高,宜采用________方式进行调查.(填“抽样调查”或“普查”)15.正比例函数的图像与反比例函数的图象相交于A 、B 两点,其中点A(2,n),且n>0,当时,的取值范围是___________________.16.(2017云南省)如图,在△ABC 中,D 、E 分别为AB 、AC 上的点,若DE ∥BC ,AD AB =13,则AD DE AE AB BC AC++++=______.17x 的取值范围为_____. 18.已知梯形的上底长为5厘米,下底长为9厘米,那么这个梯形的中位线长等于_____厘米.三、解答题19.如图,△ABC 中,AB =AC ,AD 是△ABC 的角平分线,点F 为AC 的中点,连接FD 并延长到点E ,使FD =DE ,连接BF ,CE 和BE .(1)求证:BE =FC ;(2)判断并证明四边形BECF 的形状;(3)为△ABC 添加一个条件,则四边形BECF 是矩形(填空即可,不必说明理由)20.如图所示,△ABC 中,AB =AC ,AD 平分∠BAC ,点G 是BA 延长线上一点,点F 是AC 上一点,AG =AF ,连接GF 并延长交BC 于E .(1)若AB =8,BC =6,求AD 的长;(2)求证:GE ⊥BC .21.如图,在一条不完整的数轴上从左到右有点A ,B .将线段AB 沿数轴向右移动,移动后的线段记为A′B′,按要求完成下列各小题(1)若点A 为数轴原点,点B 表示的数是4,当点A′恰好是AB 的中点时,数轴上点B′表示的数为 .(2)设点A 表示的数为m ,点A′表示的数为n ,当原点在线段A′B 之间时,化简|m|+|n|+|m ﹣n|.22.如图,某校准备给长12米,宽8米的矩形ABCD 室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形PQFG ),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点O 为矩形和菱形的对称中心,OP AB ,2OQ OP =,12AE PM =,为了美观,要求区域Ⅱ的面积不超过矩形ABCD 面积的18,若设OP x =米.x=时,求区域Ⅱ的面积.(1)当3(2)计划在区域Ⅰ,Ⅱ分别铺设甲,乙两款不同的深色瓷砖,区域Ⅲ铺设丙款白色瓷砖,①在相同光照条件下,当场地内白色区域的面积越大,室内光线亮度越好.当x为多少时,室内光线亮度最好,并求此时白色区域的面积.x=米时,购买三款瓷砖的总费用最少,且最少②三种瓷砖的单价列表如下,,m n均为正整数,若当2费用为7200元,此时m=__________,n=__________.23.某厂为新型号电视机上市举办促销活动,顾客每买一台该型号电视机,可获得一次抽奖机会,该厂拟按10%设大奖,其余90%为小奖。
广东省佛山市南海区石门实验中学2019-2020学年八年级下学期第一次阶段检测

石门实验中学2019-2020学年第二学期英语学科第一次教学检测班级_________ 姓名_________ 学号_________全卷共6页,考试用时为50分钟,满分100分一、语法选择(本大题有10小题,每小题2分,共20分)在每小题四个选项中,选出可以填入空白处的最佳答案,将其字母编号填在题号前的括号内。
There are many optimistic(乐观的)people around us. 1 person I have ever seen is my dad!He is so positive that I have never heard 2 single word from him which is related to hopelessness!Unlike most mums and dads,my dad never says things that 3 make me feel sad. He is always there to give 4 encouragement and help. When I do something wrong,he always tells me 5 I should do next time in a positive way. For example,if I am 6 trouble,he often tells me to open the books he has bought for me. Then he asks me 7 the stories that can help me with the problems I'm facing. After that,we will have a discussion together. If it's useless,he 8__ me calm down firstly and think about what happened to me by myself.9_ I'm not always a good kid because of my naughty character,my dad never shouts at or gets angry with me. I know that he's waiting for the day when I grow up and understand some important things in my life.I can see the reason why he is so positive is that he believes in himself,and also I __ 10 __ by him. He believes that whatever happens,it is under control. So we have nothing to worry about. Be positive!Sunshine will be in your life forever.( )1.A.Most optimistic B. Optimistic C. More optimistic D. The most optimistic ( )2.A.the B./ C. an D. a( )3.A.should B. need C. must D. may( )4.A.my B. me C.I D. myself( )5.A.which B. what C. why D. when( )6.A.in B. of C. at D. with( )7.A.to read B. read C. reads D. reading( )8.A.let B. letting C. has let D. will let( )9.A.Although B. Unless C. Whether D. Since( )10.A.trust B. am trusted C. trusted D. was trusted二、完形填空(本大题有10小题,每小题2分,共20分)通读下面短文,掌握其大意,然后在各小题所给的四个选项中,选出一个最佳答案,将其字母编号填写在题号前的括号内。
广东佛山南海区石门实验学校2019—2020学年度第一学期第一次质量检测八年级(PDF版,无答案)

12、比较大小:2.5
13、如图为某楼梯,测得楼梯的长为 5 米,高 3 米,计划在楼梯表面铺地毯,地毯的长度至
少需要
米。
14、若规定结果精确到 1,那么 的估算值为
15、已知△ABC 的三边长分别是 6,8,10,则△ABC 的面积是 16、如图,有一连串直角三角形,已知第一个直角三角形 OAA1 是 等腰直角三角形,且且 OA1=A1A2=A2A3=A3A4=……=A8A9=1, 则 OA9=
(1) 的整数部分是
;小数部分是
。
(2)1+ 的整数部分是
,小数部分是
。
(3)若设 2+ 整数部分为 x,小数部分为 y,求 y—xy 的值。
B
23、(1)列方程解几何题是常用解题方法: 如图 1,Rt△ABC 中,∠C=90°,AB 比 AC 长 1,BC=3,求 AC 的长。
解:设 AC 为 x,则 AB=x+1. 在 Rt△ABC 中,AC2+ BC2= AB2
1
石门实验学校 2019—2020 学年度第一学期第一次质量检测
17、观察下列运算过程:
=
=
=
+
+(
) ()
=
+
+(
请运用上面的运算方法计算:
= ) ()
当 n=99 时,
+
+
+
+
+
+…+
=
++
= ()
三、解决问题(一) 18、计算:(1)
(2)( + )×
19、计算:( + )× +( +1)(
C. 与
D.-5 与∣-5∣
6、下列说法正确的是(
)
A.无限小数是无理数 B.只有整数才有平方根 C. -2 是 4 的平方根
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东省石门实验中学2019-2020学年八年级下学期第一次月考数学
试题(word无答案)
一、单选题
(★) 1 . 式子:①2>0;②4x+y≤1;③x+3=0;④y-7;⑤m-2.5>3.其中不等式有( )
A.1个B.2个C.3个D.4个
(★) 2 . 在代数式,,,a+ 中,分式的个数是()
A.2B.3C.4D.5
(★) 3 . 下列方程:① ;② ;③ ;④ ;⑤ .其中是分式方程的是( )
A.①②B.②③C.③④D.②③④
(★★) 4 . 下列等式从左边到右边的变形,属于因式分解的是( )
A.2ab(a-b)=2a2b-2ab2B.x2+1=x(x+)
C.x2-4x+3=(x-2)2-1D.a2-b2=(a+b)(a-b)
(★★) 5 . 不等式的解集在数轴上表示正确的是()
A.B.C.D.
(★) 6 . 今年四月份,李大叔收获洋葱30吨,黄瓜13吨.现计划租用甲、乙两种货车共10辆将这两种蔬菜全部运往外地销售,已知一辆甲种货车可装洋葱4吨和黄瓜1吨,一辆乙种货车可装洋葱和黄瓜各2吨.李大叔租用甲、乙两种货车时有()种方案.( )
A.1B.2C.3D.4
(★★) 7 . 不等式组的解集在数轴上表示正确的是()
A.B.
C.D.
(★★) 8 . 下列变形从左到右一定正确的是()
A.B.C.D.
(★★) 9 . 如图,函数和的图象相交于A(m,3),则不等式的解集为()
A.B.C.D.
(★) 10 . 已知关于 x的不等式的解集为,则 a的取值范围是( )
A.a>4B.a<4C.a≠4D.a≥4
二、填空题
(★) 11 . 分解因式: ________ .
(★) 12 . 不等式3 x-7≥2的最小整数解是____________.
(★) 13 . 如图,一次函数y=kx+b的图像经过A、B两点,那么关于x的不等式kx+b>0的解集是_____.
(★) 14 . 若 a> b,且,则 b_______0.(填“>”或“<”)
(★) 15 . 化简:= ________ .
(★) 16 . 方程的解是_______.
(★) 17 . 若分式的值为零 , 则 .
(★) 18 . 如图,直线经过两点,则不等式的解集为
_______________。
(★) 19 . 已知,则的值为_______.
(★★) 20 . 计算:的结果是(结果化为最简形式) _____ .
三、解答题
(★) 21 . 先化简,再求值:,在﹣2,0,1,2四个数中选一个合适的代
入求值.
(★) 22 . 某公司准备把240吨白砂糖运往 A, B两地,用大、小两种货车共20辆,恰好能一次性装完这批白砂糖,相关数据见下表:
载重量运往A地的费用运往B地的费用
大车15吨/辆630元/辆750元/辆
小车10吨/辆420元/辆550元/辆
(1)求大、小两种货车各用多少辆?(2)如果安排10辆货车前往A地,其中大车有m辆,其余货车前往B地,且运往A地的白砂糖不少于115吨,
①求m的取值范围;
②求当 m=7时,总运费是多少?。
