二次根式第一课时-史春雷(1)
16.1二次根式第1课时课件

呢?
5
形如 a (a≥0)的式子叫做二次根式
(1)表示a的算术平方根; (2)a可以是数,也可以是代数式; (3)从形式上看,含有二次根号; (4)a≥0, a ≥0.
例:下列各式中,哪些是二次根式?并指出二 次根式中的被开方数.
7, 22 , 4 10, x 3(x 3), y 1 y 1, x 12 , x2 3, y xy 0
解:由a+1≥0,得a≥-1. ∴字母a的取值范围是大于或等于-1的实数.
2 1
1 2a
解:由
1 1 2a
>0,得1-2a>0,即a
<
1 2
∴字母a的取值
范围是小于
1 2
的实数.
3 a - 32
解:因为无论a取何值,都有(a-3)2≥0,所以字母a 的取值范围是全体实数.
4 a 1
解:因为无论a取何值,都有|a|+1>0,所以字母a的 取值范围是全体实数.
在分母上,因此 2x 1 解得x > 1 .故选C.
≠0.则22xx
1 1
0, 0.
2
3.当x= -3 时,二次根式 x + 3 有最小
值,其最小值是 0 .
解析: ∵二次根式有意义,∴x+3≥0,即x+3 的最小值是0,∴x+3=0,解得x=-3.
4.求下列各式中字母a的取值范围: 1 a +1
x
解: 7,x-3 x 3, x 12, y (xy>0)
x y
是二次根式.其中被开方数依次是7,x-3,(x+1)2,x .
[解题策略] ①当被开方数形式是含有字母的代数式时, 可以把这个代数式看成一个整体.如 x2 2015 的被开方数是 x2 2015.
八年级下册数学课件(鲁教版)二次根式的性质 第一课时

例题引领
例1(1Βιβλιοθήκη 36(2) 9 43
0.5
4
a
x2
2
6 20
=
6 20
ab a b(a≥0,b≥0) 利用它可以对二次根式进行化简.
(2) 27
(3) 4a2
65 10 7
12 15x4y3
小试牛刀
化简:
(1) 12 (2) 27 15
明确目标
1.理解掌握a2的算术平方根公式 ( a )2 a (a≥0),并会利用它进行计算和化简. 2.理解积的算术平方根 ab= ·a (ba≥0,b≥0) 并利用它进行计算和化简.
知识铺垫
1. 形如 (aa≥0)的式子叫做二次根式.
其中a为整式或分式,a叫做被开方式.
特点:①都是形如 a 的式子,
②a都是非负数.
2.因为 a (a ≥ 0)表示a的算术平方根,所以 a ≥ 0(a ≥ 0);
( a )2 a(a≥ 0); a ( a )2 (a≥ 0).
(1)计算 22 , 32 , 1 2 , 02的值,你发现了什么? 2
(2)当a ≥ 0时, a2的算术平方根是多少?由此你能得到 一个怎样的等式? 当a ≥ 0时, a2 a.
(3) 4a3
化简二次根式,就要把被开方数 中的平方数(或平方式)从根号里 开出来.
1. 当a ≥ 0时, a2 a.
2. 当a ≥ 0时, ( a )2 a2 .
3.
苏教版二次根式教案第一课时

苏教版二次根式教案第一课时教案标题:苏教版二次根式教案第一课时教学目标:1. 理解二次根式的概念和性质。
2. 掌握二次根式的化简和运算方法。
3. 能够应用二次根式解决实际问题。
教学准备:1. 教材:苏教版二次根式教材。
2. 教具:黑板、粉笔、教学PPT等。
3. 学具:练习册、作业本等。
教学步骤:Step 1:导入新知1. 引导学生回顾一元二次方程的知识,通过问题引入二次根式的概念。
2. 提问:“什么是二次根式?二次根式有哪些特点?”引导学生思考并回答。
Step 2:概念解释与讲解1. 通过教学PPT或板书,对二次根式的定义进行解释,并给出示例。
2. 讲解二次根式的基本性质,如二次根式的分子中不含有平方根、二次根式的和差化简等。
Step 3:化简与运算1. 引导学生通过例题掌握化简二次根式的方法,如合并同类项、有理化分母等。
2. 通过练习题让学生巩固化简二次根式的基本技巧。
3. 引导学生通过例题和练习题掌握二次根式的加减乘除运算方法。
Step 4:应用解决实际问题1. 设计一些与实际生活相关的问题,引导学生运用二次根式解决问题。
2. 分组讨论和展示解题过程,加深学生对二次根式应用的理解。
Step 5:小结与作业布置1. 对本节课所学内容进行小结,强调二次根式的概念、性质和运算方法。
2. 布置相应的课后作业,巩固所学知识。
教学延伸:1. 对于学习较快的学生,可以提供更多的挑战性练习,如复杂的二次根式运算或解决实际问题。
2. 对于学习较慢的学生,可以提供更多的练习机会,加强基本技能的训练。
教学反思:本节课通过引入问题、概念解释、化简与运算、应用解决实际问题等环节,全面培养学生对二次根式的理解和应用能力。
在教学过程中,教师要注重激发学生的学习兴趣,提高课堂互动,使学生能够主动思考和解决问题。
同时,教师还要根据学生的实际情况进行差异化教学,确保每个学生都能够达到预期的学习目标。
16.1二次根式(一)

培养学生合作交流的意识.
为概括二次根式的概念作铺垫。
体验数学在生活中应用的广泛性.
检测学生对知识的掌握情况及应用能力,初步体验成功的喜悦。
进一步加深学生对二次根式被开方数必须是非负数的理解.培养学生科学严谨的学习态度。
学情分析
八年级的学生大约在13岁左右,有一定的学习经验和生活经验,知道并会求一个数的平方,这些是学习本节课的知识基础。基于学生的学习基础,在研究的方法和合情推理方面还存在欠缺.他们经历一些探究的过程:动手实践、观察猜想、归纳总结、巩固应用等.因此,本节课的学习,可以引导学生通过探究研究方法.八年级的学生观察、操作、猜想能力较强,但归纳、运用数学意识的思想比较薄弱,需要在课堂教学中进一步加强引导。根据学生的认知特点和接受水平,本节课把学生掌握知识作为教学的主线,同时也为学习下节课的内容打好坚实的基础。
(2)一个长方形围栏,长是宽的2倍,面积为130m?,则它的宽为______m.
(3)一个物体从高处自由落下,落到地面所用的时间t(单位:s)与开始落下的高度h(单位:m)满足关系h=5t?,如果用含有h的式子表示t,则t=_____.
问题2:上面得到的式子 , , 分别表示什么意义?它们有什么共同特征?
A. B. C. D.
2.当 时,二次根式 无意义.
3.当 时,二次根式 有最小值,其最小值是.
4.对于 ,小红根据被开方数是非负数,得 出的取值范围是 ≥ .小慧认为还应考虑分母不为0的情况.你认为小慧的想法正确吗?试求出 的取值范围.
(2)4的算术平方根为2,用式子表示为 =__________;正数a的算术平方根为_______, 0的算术平方根为_______;式子 的意义是。
八年级数学下册教学课件《二次根式》(第1课时)

A B ... N
A≥0;
B≥0;
...
N≥0;
(4)二次根式与分式的和如
A≥0且B≠0.
B
有意义的条件:A>0;
A
A
有意义的条件:
1
有意义的条件:
B
巩固练习
16.1 二次根式
x取何值时,下列二次根式有意义?
(1)
x 1
(2)
x≥1
(4)
3.若 x 2 在实数范围内有意义,则x的取值范围在数轴上
表示正确的是( D )
A.
B.
C.
D.
课堂检测
16.1 二次根式
基 础 巩 固 题
1.下面的式子是二次根式的是( A )
A. a 1
2
B. 3
33
C. -1
1
D. a
2
2.二次根式 2 x 4 中的x的取值范围是( D )
A.x<﹣2
(7)
1
x
3x
x≤0
(5)
x3
x>0
x≥0
(3) 4x 2
x为全体实数
(6) 1
x 2 x≠0
x 1
( x 2)0 (8)
x3
x2
(9)
x
x≥-1且x≠2
x>0
x 1
2
x为全体实数
探究新知
16.1 二次根式
知识点 2
【回顾思考】二次根式
二次根式的双重非负性
a 的被开方数a的取值范围是什么?它
人教版 数学 八年级 下册
16.1 二次根式
16.1 二次根式(第1课时)
二次根式(1)
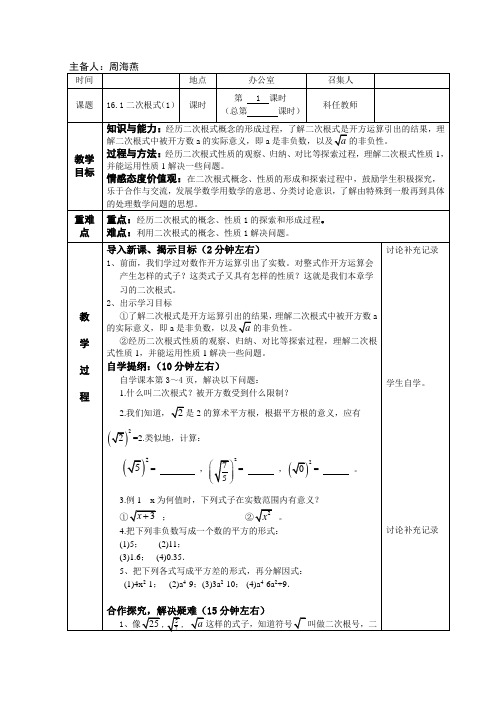
5、把下列各式写成平方差的形式,再分解因式:
(1)4x2-1;(2)a4-9;(3)3a2-10;(4)a4-6a2+9.
合作探究,解决疑难(15分钟左右)
1、像 , , 这样的式子,知道符号 叫做二次根号,二次根号下的数叫做被开方数。因为在实数范围内,负数没有平方根,所以被开方数只能是正数或零。也就是说当a≥0时, 是有意义的,它表示a的算术平方根。
情感态度价值观:在二次根式概念、性质的形成和探索过程中,鼓励学生积极探究,乐于合作与交流,发展学数学用数学的意思、分类讨论意识,了解由特殊到一般再到具体的处理数学问题的思想。
重难点
重点:经历二次根式的概念、性质1的探索和形成过程。
难点:利用二次根式的概念、性质1解决问题。
教
学
过
程
教
学
过
程
导入新课、揭示目标(2分钟左右)
3、二次根式的性质1;
布置作业,拓展延伸(8分钟)
课堂作业:
必做题:习题16.1第2,4题。
选做题:习题16.1第7题。
课外作业:习题16.1第1、3题。
讨论补充记录
学生自学。
讨论补充记录
板书
设计
一、复习引入四、课堂小结:
二、自主学习五、当堂训练
三、合作探究六、布置作业
教学反思
定义:形式如 (a≥0)式子叫做二次根式。
2、性质1 =a (a≥0)。
反之,也成立。即a= (a≥0)。
3、例1。
4、例2。
5、例3。
巩固新知,当堂训练(8分钟)
课堂小结(2分钟)
一路下来,我们结识了很多新知识,你能谈谈自己的收获吗?说一说,让大家一起来分享。
二次根式第一课时课堂实录
2.7二次根式 第一课时一. 教学目标1.认识二次根式和最简二次根式的概念,并能用二次根式的性质进行化简。
2.用类比的方法,引入二次根式的性质、公式。
3.通过二次根式的化简,培养学生抓住问题的关键来解决问题的基本思路。
二.教学重难点正确运用公式b a b a ∙=⋅(a ≥0,b ≥0),b ab a=(a ≥0, b >0)并能进行熟练地运算,理解法则中b a b a ∙=⋅(a ≥0,b ≥0),b aba=(a ≥0, b >0)a 、b各满足什么条件。
三.新旧只是连接运用二次根式是在平方根,立方根,实数的基础上,进一步研究二次根式的概念和性质。
与已学内容实数,整式和勾股定理联系紧密,同时也是以后将要学习的锐角三角函数,一元二次方程和二次函数等内容的重要基础。
本课时研究的内容是下一课时二次根式的运算的基础和依据。
做一做:填空:(1)94⨯94⨯2516⨯2516⨯=,94=;9425162516=,=;=,=;=,=.66202023234545有何发现:49⨯=1625⨯=49=1625=49⨯,1625⨯,49,1625.=,6.48067⨯76⨯=;76(2)用计算器计算:=,=.6.4800.92550.9255有何发现:6776⨯7649⨯=,49⨯1625⨯=,1625⨯49=,491625=.1625观察上面的结果你可得出什么规律?=67⨯,=67.知识巩固•例1 化简•(1);•(2);•(3)。
教师首先讲解第一个例题。
师:【根号下是81乘以64,我们应用第一个公式,就等于728964816481=⨯=⨯=⨯】教师要注意格式。
师:【就是这样简单的应用我们的公式,下面两个题同学们在课堂本上写,我找两个同学来做。
】 学生能很快地写出正确答案。
学生得出答案.35.....65.....72. 师:【我们为什么要学习二次根式的性质呢?是想去化简二化简下面的二次根式.化简:4527319816125。
内蒙古乌兰浩特市第十二中学八年级数学人教版下册教案16.1 二次根式(第一课时)
重点: 有意义的条件. 2. ≥0时 ≥0的应用. 3. 和 的运算、化简。
难点: <0时 的化简.
教学方法与手段
方法:引导启发手段:多媒体
教
学
过
程
教学内容
教师活动
学生活动
一、复习引入
用带有根号的式子填空,看看写出的结果有什么特点:
(1)要做一个两条直角边的长分别是7cm和4cm的三角尺,斜边的长应为_________________cm
16.1二次根式
问题1例1例3
问题2例2例4
问题3
教学反思
参考资料
(学生活动)议一议:
1.-1有算术平方根吗?
2.0的算术平方根是多少?
3.当a<0, 有意义吗?
例2解:由3x-1≥0,得:x≥
当x≥ 时, 在实数范围内有意义.
本节课要掌握:
1.形如 (a≥0)的式子叫做二次根式,“ ”称为二次根号.
2Hale Waihona Puke 要使二次根式在实数范围内有意义,必须满足被开方数是非负数.
板书设计
分析例题1:二次根式应满足两个条件:第一,有二次根号“ ”;第二,被开方数是正数或0.
分析例题2:由二次根式的定义可知,被开方数一定要大于或等于0,所以3x-1≥0, 才能有意义.
分析:要使 + 在实数范围内有意义,必须同时满足 中的≥0和 中的x+1≠0.
(学生活动)请同学们独立完成下列三个问题。
教案号
1
主备教师
斯琴花
授课时间
2月24日
课题
16.1二次根式(1)
课标要求
教学目标
1知识与技能:通过探究知道二次根式定义,掌握二次根式中字母的取值范围。
21.1二次根式(第1课时)
必做题
1.教材P5习题21.1
2.复习巩固1题2题(1)、(2)
4题(1)、(2)
选做题
配套练习P2. 9题
配套练习P1. 8题、
配套练习P3. 12题
教师布置作业,动员分层要求。
学生按要求课外完成
教
后
反
思
【当堂达标自测题】
一、填空题
1.16的平方根是.
(5)当x-y≥0时是二次根式,当x-y<0时不是二次根式;即当x≥y是二次根式,当x<y时不是二次根式.
2.教材第3页
练习1、2、3.
3.计算:
(1)
(1)、(2)小题学生口答。
(3)小题请学生认真思考后回答;
(4)(5)两小题需要分情况讨论,学生思考、交流.
教师可提示、点拨.
教材第3页练习
学生分小组交流合作完成,师巡视辅导有困难的学生.
2.已知一个正数的平方根是 和 ,则这个数是.
3.函数 自变量 的取值范围是.
4.当x=________时,二次根式 有意义.
二、选择题
5.下列各式中是二次根式的是()
A B C D
6.若使已知 为实数,那么 等于()
A. B. C.-1 D. 0
7.二次根式 在实数范围内有意义,则x的取值范围是
A. B. C. D.
教师提出问题(2),检查学生对所学知识的掌握情况,并引导学生将所学知识与新知识相联系。
教师提出问题(3)学生总结二次根式的概念,思考 中a≥0的作用和原因
教师出示例题,提问:二次根式有意义的条件是什么?
学生口答,独立完成例1.
师强调解体格式
师提问:x的取值范围与x的指数有什么关系?
吉林省伊通县实验中学九年级数学上册《21.1 二次根式
《21.1 二次根式》教案(第1课时)
教学目标:
知识技能:使学生理解并掌握二次根式的概念,掌握二次根式中被开方数的取值范围和二次根式的取值范围.
教学方法:启发式教学
教学手段:多媒体教学
教学准备:多媒体课件
课时:1课时
教学过程:
问题与情境
活动一回顾与思考
1.4的平方根是_____;0的平方根是______;-16的平方根是____.
2.5的平方根是_______;5的算术平方根是____.
3.直角三角形的两条直角边分别为7和4,斜边为__.
4.正方形的面积为s,则它的边长为_____.
活动二接触新知
上面3、4题的结果是,
他们表示一些正数的算术平方根.
1.二次根式的定义:一般的,我们把形如(≥0)的式子叫做二次根式,“” 称为二次根号.
2.例题与练习
例1.下列各式是否为二次根式?
(1);(2)(3);(4);(5).
(5)当x-y≥0时是二次根式,当x-y<0时不是二次根式;即当x≥y是二次根式,当x<y时不是二次根式.
当x≤时,在实数范围内有意义;
(3)由-5x≥0,得x≤0;
当x≤0时,在实数范围内有意义;
(4)∵≥0,
∴+1>0,
∴x为任意实数都有意义.
练习:
1. 一个矩形的面积是18cm2,它的边长之比为2:3,它的边长应为多少?
2.当是怎样的实数时,下列各式在实数范围内有意义?
教学后记:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( a)
a
2
2
读作: 的算术平方根的平方 的算术平方根的平方. 读作:a的算术平方根的平方 读作: 的平方的算术平方根 的平方的算术平方根. 读作:a的平方的算术平方根
(3)取值范围不同 )
( a)
2
= a(a ≥ 0)中,必必必必a ≥ 0,即a是一个非负数.
a 2 = a 中, a可取一可实数
(4)意义不同,运算顺序也不同 )意义不同,运算顺序也不同.
2 2
( )
2
(3) 0.3 (5) −
; .
(−π)
=
-π ; (6) 10 =
−2
1 10
2.要画一个面积为 要画一个面积为18cm²的矩形,使它的 的矩形, 要画一个面积为 的矩形 长宽之比为3:2,它的长宽应取多少? 长宽之比为 ,它的长宽应取多少? 解:设矩形的长宽分别为3x和2x. 设矩形的长宽分别为 和 由题意得, 由题意得,3x·2x=18, , 所以
(−3)2 = 3 02 =
0
; .
a =a =
2
a (a > 0) 0 (a = 0) . − a ( a < 0)
Hale Waihona Puke 例3化简1 ()
16;
(2)
2
( - 5) .
2
解: 1 ()
16 = 4 = 4;
2
(2) - 5) = (
5 =5
2
( a) 与
2
a 的的别与联系
2
的别: ) 的别: 1)写法不同 ( (2)读法不同 )
a -1 0 b 1 2
解:由数轴可知,a<0,b>0,a-b<0, 由数轴可知, 所以原式=-a-b+|a-b| 所以原式 =-a-b+(b-a)=-2a
6.请你比较2 3与3 2的大小.
Q 解: 2 3
( ) = 2 ×( 3) = 4 × 3 = 12 (3 2 ) = 3 ×( 2) = 9 × 2 = 18 ∴ (2 3 ) < (3 2 )
在上面的问题中, 在上面的问题中,结果分别是 13 , S , 它们都表示一些正数的算术平方根. 2 , h ,它们都表示一些正数的算术平方根
5
我们知道, 个平方根; 我们知道,一个正数有 两 个平方根; 0的平方根为 0 ;在实数范围内, 在实数范围内, 的平方根为 平方根.因此 开平方时, 因此, 负数 没有 平方根 因此,开平方时, 被开方数只能是 正数 和 0 . 一般地, ( 一般地,我们把形如 a a ≥ 0) 的式 子叫做二次根式 “ 二次根式, 子叫做二次根式,” ”称为二次根号. 称为二次根号
表示a的算术平方 当a>0时, a 表示 的算术平方 时 表示0 根,因此 a > 0 ;当a=0时, a 表示 时 的算术平方根, 这就是说, 的算术平方根,因此 a = 0 .这就是说, 这就是说
(a ≥ 0)是一个 非负数 . a
a≥0是非负数, a ≥ 0 是非负数, 是非负数 也是一个 非负数,所以, 非负数,所以,算术平方根具有双重 非负性. 非负性
1 ( ) x + 2;
(2) 3 + x;
(3) 5x;
答案:( ) 答案:(1)x≥-2 :( (3)x≥0 )
(4) − x;
(2)x≥-3 ) (4)x≤0 )
填空: 填空:
( 4)
2
=
2
4
1 3
; ;
1 = 3
( 2) = ( 0) =
2 2
2 0
;
.
性质1: 性质 :
若羌县中学
史春雷
一般地,如果一个正数 的平方等 一般地,如果一个正数x的平方等 于a,即x²=a,那那这个正数 叫 , ,那那这个正数x叫 的算术平方根. 做a的算术平方根 a的算术平方根 的算术平方根 的算术平方根 .0的算术平方根是 的算术平方根是0. 记为 a(a > 0) 的算术平方根是 一般地,如果一个数的平方等于 , 一般地,如果一个数的平方等于a, 那那这个数叫做a的平方根或二次方 那那这个数叫做 的平方根或二次方 这就是说, 那那x 根.这就是说,如果 x 2 = a , 那那 这就是说 叫做a的平方根 的平方根. ( 叫做 的平方根 记为x = ± a a ≥ 0) .
( a)
2
= a ( a ≥ 0) 表示a的算术平方根的 表示 的算术平方根的
平方,先计算 的算术平方根 再求平方. 的算术平方根, 平方,先计算a的算术平方根,再求平方
表示的是 的平方的算术平方 a = a 表示的是a的平方的算术平方
2
的平方, 根,先计算a的平方,再求算术平方根 先计算 的平方 再求算术平方根.
2 2 2 2 2 2 2 2
∴2 3 < 3 2
是整数, 7. (1) 18 - n 是整数, 求自然数n的值; 求自然数n的值; 是整数, (2) 24n 是整数, 求正整数n的最小值. 求正整数n的最小值.
是完全平方数, 解:(1)由题意知,18-n是完全平方数, :( )由题意知, 是完全平方数 所以18-n=1或4或9或16. 所以 或 或 或 所以n的值为 的值为17或 或 或 所以 的值为 或14或9或2. 是完全平方数, (2)由题意知,24n是完全平方数, )由题意知, 是完全平方数 24的倍数中最小的完全平方数是 的倍数中最小的完全平方数是144, 的倍数中最小的完全平方数是 , 所以24n=144,所以 的最小值为 的最小值为6. 所以 ,所以n的最小值为
3 a≥ 2
3 a≥ - . 2
时, 2a + 3在实
数范围内有意义. 数范围内有意义
练习 1.判断下列哪些式子是二次根式 判断下列哪些式子是二次根式. 判断下列哪些式子是二次根式
3 1) a 2 ;(2) m;(3) a;(4) x + 1; 2 (
(5) 5;(6) a - b a ≥ b);( 7) - x - 1. (
2
)(4)( )(6)是二次根式. 解:(1)( )( )( )是二次根式 :( )( )(5)( 注意:判断一个式子是否是二次根式, 注意:判断一个式子是否是二次根式,不 仅要看形式,还要看是否具备a≥0的条件. a≥0的条件 仅要看形式,还要看是否具备a≥0的条件.
3.当x是怎样的实数时,下列各式在实数 当 是怎样的实数时 是怎样的实数时, 范围内有意义? 范围内有意义?
学习目标
1.理解二次根式的概念. 2.学习并掌握二次根式的性质.
1.一个三角形两直角边的长分别 一个三角形两直角边的长分别 是2cm和3cm,斜边长应为 13 cm. 和 , 2.面积为 的正方形的边长为 面积为s的正方形的边长为 面积为
S
.
3.要修建一个面积为 要修建一个面积为6.28m²的圆形喷 要修建一个面积为 的圆形喷 水池, 水池,它的半径为 2 m(π取3.14) ( 取 ) 4.一个物体从高处自由落下,落到地面 一个物体从高处自由落下, 一个物体从高处自由落下 所用的时间t(单位: ) 所用的时间 (单位:s)与开始落下时 的高度h(单位: )必必关系h=5t².如 的高度 (单位:m)必必关系 如 h . 果用含有h的式子表示 的式子表示t, 果用含有 的式子表示 ,则t= 5
2 1
B(5,3)
o
1
2
3
4
5
6
7
x
AB 2 + AC 2
2 2
= 3 +2 = 13
2009 4.已知 a + 2 + b - 1 = 0,那那( a + b) 的值为 -1 .
解:由题意知,a+2=0且b-1=0,所以 由题意知, 且 , 2009 2009 a=-2,b=1, , , 所以( a + b) = - 1) = -1 ( 5.实数 、b在数轴上的位置如图所示, 实数a、 在数轴上的位置如图所示 在数轴上的位置如图所示, 实数 2 化简: 化简: a 2 - b 2 + ( a - b) .
感谢大家的参与!再见!
x= 3
所以它的长宽分别为 3 3和2 3.
y
3.如右图,在平面直角 坐标系中,A(2,3), B(5,3),C(2,5)是 三角形的三个顶点, 求BC的长. 由题意知, 解:由题意知, AB=5-2=3, AB=5-2=3, AC=5-3=2, ,
所以 BC =
7 6
C(2,5)
5 4 3
A(2,3)
联系: 联系: 1.它们都是二次根式 它们都是二次根式 2.它们都是非负数 它们都是非负数 3.当a≥0时, 当 时
( a)
2
= a = a.
2
练习 1.说出下列各式的值: 说出下列各式的值: 说出下列各式的值
(1 )
( 3)
2
=
2
3 ; (2) 3 2 = 18 ;
1 1 = 0.3 ; (4) − = 7 7
( a)
2
= a (a ≥ 0) .
例2
计算
1 ()
解:1) (
( 1. 5 ) ;
2
(2) 2 5 .
( 1 .5 )
2
( )
2
2
= 1.5;
2
(2) 2 5
( )
=2 ×
( 5)
2
= 4 × 5 = 20.
填空: 填空:
22 = 2 = 3
性质2: 性质 :
2
2
2 3
; ;
是怎样的实数时, 例1 当a是怎样的实数时,下列各 是怎样的实数时 式在实数范围内有意义? 式在实数范围内有意义?
