第三章扩展式博弈与完全信息动态博弈
第3讲 完全信息动态博弈

最优化的一阶条件意味着: s(q1) (a q1 c) =1 2 2
第3讲 完全信息动态博弈
假定q1 a c。这实际上是库诺特模型中企业2的反应函数,不同的 是,这里,s(q1)是当企业1选择q1时企业2的实际选择,而在库诺 2 特模型中,R2 q1)是企业2对于假设的q1的最优反应。 ( 因为企业1预测到企业2将根据s(q1)选择q 2,企业1在第一阶段的问 2 题是: max 1 = q1,s(q1)=q1 a q1 s(q1) c) ( 2 2
第3讲 完全信息动态博弈
• 这个例子也说明,在博弈中,拥有信息优势可能 使参与人处于劣势,而这在单人决策中是不可能 的。企业2在斯坦克尔伯格博弈中的利润之所以低 于库诺特博弈中的利润,是因为它在决策之前就 知道了企业1的产量。即使企业1先行动,但如果 企业2在决策之前不能观测到企业1的产量,我们 就回到了库诺特均衡,因为此时,企业1的先动优 势就不存在了。
第3讲 完全信息动态博弈
* 1 回忆一下,在上一讲得到的库诺特模型的纳什均衡是q1 =q* = (a c), 2 3 3 比较这两个结果,发现斯坦克尔伯格均衡的总产量 (a c)大于库诺特 4 2 的总产量 (a c)。但是,企业1的斯坦克尔伯格均衡产量大于库诺特 3
均衡产量,而企业2的斯坦克尔伯格均衡产量小于库诺特均衡产量。 因为企业1本来可以选择库诺特均衡产量但它没有选择,说明企业1在斯坦 克尔伯格博弈中的利润大于库诺特博弈中的利润,而总产量上升意味着 总利润下降了从而企业2的利润一定下降了。这就是所谓的“先动优势”。
第3讲 完全信息动态博弈
• 宏观经济政策的动态一致性 宏观经济学上与子博弈精炼纳什均衡相对应的概 念是政府政策的动态一致性(dynamic consistency 或time consistency)。政府政策 的动态一致性指的是,一个政策不仅在制定阶段 应该是最优的(从政府的角度),而且在指定之 后的执行阶段也应该是最优的,假设没有任何新 的信息出现。如果一个政策只是在制定阶段是最 优的,而在执行阶段并不是最优的,这个政策就 是动态不一致的。说它是动态不一致的,是因为
第三章 完全信息动态博弈 ppt课件

条路径。但每条路径可由不同的策略组合决定。
例如, (开发,(不开发,开发))决定了
A -> 开发 -> B -> 不开发 -> (1,0)
该路径还可由(开发,(不开发,不开发))决定。
事实上,该问题共有4条路径,8种策略组合。
ppt课件
12
§2 子博弈精炼纳什均衡
对于动态博弈,Nash均衡可能并不是一个合理的预测。 如房地产博弈:
又如,上例中,如果进入者先行动,而在位者在 行动前能准确知道前者的行动,那么在位者的信息 集为 {进入}或{不进入}。 反之,若在位者先行动, 则在位者的信息集为{进入,不进入}。
ppt课件
7
三、 动态博弈的相关概念
(3) • 完美信息(Perfect information):一个局中人在行动
时,对之前博弈进程有准确了解,即每一个信息集只包含 一个值,则称该局中人具有完美信息。 • 如果动态博弈的所有局中人都有完美信息,则称为完美信 息的动态博弈。 • 如果动态博弈中,存在部分局中人具有不完美信息,称为 不完美信息的动态博弈。
思考:若进入者真的进入,在位者的最优行动是“默许”。 所以“斗争”是一种不可置信的威胁(即使在位企业摆出 一副“你进入我就斗争”的架势,进入企业不应被吓到)。 而静态博弈承认这种不可置信的威胁,使(不进入,斗争) 成为一个Nash均衡。
动态博弈解决方案:剔除不可置信的威胁策略
ppt课件
3
扩展阅读:不可置信的威胁策略 引出信息经济学重要的概念—— 承诺行动(Commitment)。
ppt课件
18
三、 逆向归纳法求解子博弈精炼Nash均衡
• 从动态博弈的最后一个阶段局中人的行为开始分析
第三讲 完全信息动态博弈
第三章完全信息动态博弈第一节完全信息动态博弈的扩展式表述动态博弈的根本特征是,参与人的行动有先后顺序,且后行动的参与人在自己行动之前能观测到先行动的参与人的行动,特别是能根据先行动的参与人的行动调整或做出自己的战略选择。
运用战略式表述动态博弈的缺陷表现在:1.看不出行动的先后顺序;2.对于描述2人以上的博弈较不方便。
因此,扩展式表述extensive form representation被用于描述动态博弈。
一、扩展式表述的要素1.参与人集合:i=1,……,n。
此外,用N代表虚拟参与人“自然”。
2.参与人的行动顺序the order of moves:谁在什么时候行动。
3.参与人的行动空间action set:在每次行动时,参与人有些什么选择。
4.参与人的信息集information set:每次行动时,参与人知道些什么。
5.参与人的支付函数:在行动结束之后,每个参与人得到些什么(支付是所有行动的函数)。
6.外生事件(即自然的选择)的概率分布。
如同两人有限博弈的战略表述可以用支付矩阵表示一样,n人有限博弈的扩展式表述可以用博弈树game tree表示。
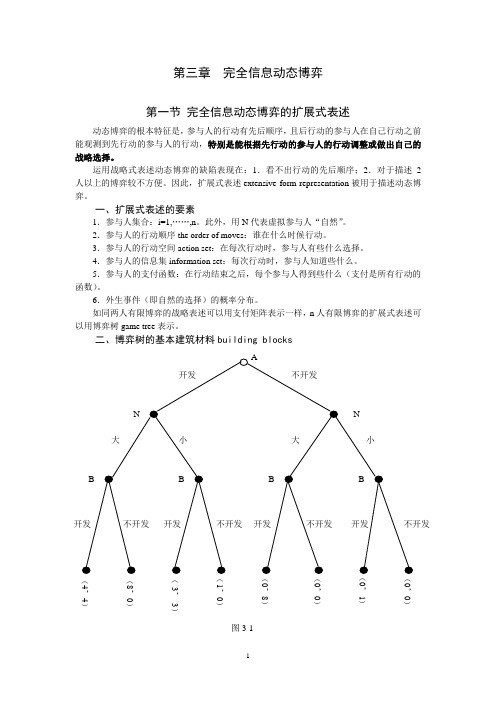
二、博弈树的基本建筑材料building blocks(4,4)(8,)(-3,-3)1,),8),),1),)图3-1(一)结nodes1.结的分类(1)决策结decision nodes:参与人采取行动的时点。
包括:起点结——initial nodes非起点结——(2)终点结terminal nodes:博弈行动路径的终点。
2.结的顺序关系precedence relation用X表示所有结的集合,x∈X表示某个特定的结。
x≺x"表示“x在x"之前”≺3.前列集the set of predecessors和后续集the set of successors定义P(x)为在x之前的所有结的集合,简称为x的前列集;定义T(x)为x之后的所有结的集合,简称为x的后续集。
经济博弈论_谢识予_2_完全信息动态博弈0.1

单结信息集:只包含一个决策结的信息集 完美(Perfect)信息:博弈树的所有信息都是单结的。 ——博弈中没有任何参与人同时行动,且后行动者能观察到先 行动者的行动,且所有参与人观察到N的行动)
1 动态博弈的扩展式表述
静态博弈用扩展式表述 A
坦白 抵赖 坦白
Q:何为完 全信息? B
抵赖
囚 徒 困 境 博 弈
-3,-3 -4,-3
-3,-3 0,0
1,-2 -4,-3 割耳
1,-2 0,0 (-3,-3) (1,-2) 默认 割耳 (-4,-3) (0,0)
三个NE: (不画,{割耳,默认}) (画,{默认,割耳}) (画,{默认,默认})
画 小孩 不画
父亲
父亲
默认
4 NE的缺陷——不可置信的威胁
换句话说,与抽烟有关决策不是单人在中性环境中 的决定,而是一种博弈。“今日卡门”和不同偏好的卡 门自己,即“未来卡门”间的博弈。
5 逆向归纳法
继续抽 未来的 卡门 不抽 今天的卡门
-1,1
1,-1
0,0 两个“卡门”如何行事? 未来卡门如何行事? 考虑到未来卡门的未来行动,今日卡门今日如何行事?
2 动态博弈中的策略
博弈树中参与人在结点上所选择的单个行动—— 一步/招 (move)
美中军事博弈
但是,参与人可以制定一个行动计划,将每个决策结上 的选择都事先规定好,即使这个决策点实际上不会出 美国 现。——策略
中国 中国
策略: 人不犯我、我不犯人; 人若犯我、我必犯人
不犯人
(-2,-2) (2,-4) (3,-5) (0,0)
4 NE的缺陷——不可置信的威胁
第三章扩展型博弈论

如果甲先行动,但在博弈开始前商铺主乙有一次行动A的机会, 请利用子博弈完美纳什均衡概念分析下述两种情况下的博弈结果
(1)A:商铺主乙逢人便说自己一定要进货,无论对方如何行 动他都不会改变这个决定;
(2)A:商铺主乙与某个嘲笑他说大话的第三者丙打赌:如果 自己到时不进货,向丙支付1500元;如果自己到时候进货,丙 向他支付100元。并且,乙将这个赌局通知甲。
甲
甲
进 乙
不进 乙
进 乙
不进 乙
进
不进 进
不 进
进
不进 进
不 进
(-1000,-1000) (0,1000) (0,0)(-1000,-900)
(0,1100)(0,-1500)
(1000,0)
(1000,-1500)
作业: 阅读“蜈蚣博弈”
拍卖人拿出一张10元钞票,请大家给这张
钞票开价,无底价,竞拍者可无限制的轮 流叫价,每次叫价的增幅以5毛为单位,出 价最高者可以得到这张10元钞票,但出价
即每阶段都选“不坦白”,A总得益贴现为
2 ( 2 ) ( 2 ) 2 .. . 2
当
1(6) 2 1 1
1 时,A选“不坦白”是最优的,即
当
1 5
时,A在没有人先选“坦白”时选“不坦白”是最优的,并且A 在之后每阶段都选“不坦白”是最优的选择。
乙
甲
坦白 不坦白
坦白 -6,-6 -1,-8
最高和次高者都要向拍卖人支付出价数目 的费用。
——苏比克拍卖模型
第四节
重复博弈
重复博弈
单次博弈重复进行构成的博弈过程,但博 弈方的行为和博弈结果不一定是单次博弈 的简单重复,其中,单次博弈可称为阶段 博弈
博弈论以及应用之3完全且完美信息动态博弈[1].pptx
![博弈论以及应用之3完全且完美信息动态博弈[1].pptx](https://img.taocdn.com/s3/m/6f1c58c72cc58bd63186bd7d.png)
3.8 空头承诺II
回顾
在前述产品开发博弈中,均衡结果(不开发,(开发,开发)) 就是企业A的空头承诺,是不可置信的。
生活中的空头承诺
学生对老师的承诺
老师,这回让我过吧,以后我会好好学习的 老师,先发表一篇达到毕业要求,以后一定会写核心期刊的
山盟海誓
爱你一万年 海枯石烂
1,0 0,0
纳什均衡
企业A开发B不开发
➢ (开发,(不开发,开发)) ➢ (开发,(不开发,不开发))
企业A 不开发B开发
➢ (不开发,(开发,开发))
2020/3/4
9
3.3 动态博弈中的行为与战略VII
总结:动态博弈的矩阵描述存在的问题
战略空间复杂
后行动者的战略空间随局中人的数量和每一阶段局中人的行 动选择数量而急剧增大
25
3.9 承诺行动IV
绑架与劫持中的承诺行动
对峙中的谈判
拒绝谈判
➢ 历史上拒绝谈判曾是一种高效方法,汉武帝和曹操都用过 ➢ 实际生活中拒绝谈判也是一种重要策略 ➢ 交出控制权是拒绝谈判的一种具体形式
谈判中的承诺
➢ 歹徒的承诺可信吗?
职业歹徒的承诺是可信的,因为他们在树立和维护自己的声誉 非职业歹徒的承诺可能也是可信的,因为他们可能不想罪加一等
先行者:美国 后行者:中国
2020/3/4
4
3.3 动态博弈中的行为与战略II
模型描述
战略空间
美国——先行者
➢ 战略就是行动
中国——后行者
➢ 战略是针对先行者各种可能行动而制定的行动方案,包括 美国犯我,我犯人;美国不犯我,我犯人 美国犯我,我不犯人;美国不犯我,我不犯人 美国犯我,我犯人;美国不犯我,我不犯人 美国犯我,我不犯人;美国不犯我,我犯人
博弈论与信息经济学讲义5
• • •
一 博弈扩展式表述 二 子博弈精练纳什均衡
扩展式表述博弈的纳什均衡
子博弈精练纳什均衡 用逆向归纳法求子搏弈精练纳什均衡
•
•
承诺行动与子搏弈精练纳什均衡
逆向归纳法与子搏弈精练纳什均衡的存在问题
三 应用举例
博弈的划分
博弈的划分: 从参与人行动的先后顺序:静态博弈和动态博弈
静态博弈:参与人同时选择行动或非同时行动但后 行动者并不知道前行动者采取了什么具体行动;
不开发
B
开发
x
不开发
B
开发
x’
不开发
(-3,-3)
(1,0) (0,1)
(0,0)
扩展式 A
开发
不开发
纳什均衡与均衡结果:
存在三个纯战略纳什均衡: (不开发,(开发,开发)), (开发,(不开发,开发), (开发,(不开发,不开发)) 两个均衡结果: (开发,不开发) (不开发,开发)
• • • • •
一 博弈扩展式表述 二 子博弈精练纳什均衡
扩展式表述博弈的纳什均衡 子博弈精练纳什均衡 用逆向归纳法求子搏弈精练纳什均衡 承诺行动与子搏弈精练纳什均衡 逆向归纳法与子搏弈精练纳什均衡的存在问题
三 应用举例
战略的表述
战略:参与人在给定信息集的情况下选择行动的规则, 它规定参与人在什么情况下选择什么行动,是参与人 的“相机行动方案”。
开发
若A先行动,B在知道A的行动后行动,则A 有一个信息集,两个可选择的行动,战略 空间为:(开发,不开发); B有两个信息集,四个可选择的行动,B有 四个纯战略: 开发策略:不论A开发不开发,我开发; 追随策略:A开发我开发,A不开发我不开 发; 对抗策略:A开发我不开发,A不开发我开 发; 不开发策略不论A开发不开发我不开发, 简写为: (开发,开发),(开发,不开发), (不开发,开发),(不开发,不开发), 括号内的第一个元素对应A选择“开发”时 B的选择,第二个元素对应A选择“不开发” 时B的选择。
(完整版)完全信息动态博弈.ppt
(四)参与人在博弈树中的顺序
1、排序的基本原则
一个参与人在决策之前知道的事情必须出现在该 参与人的决策结之前。
2、自然人的排序
– 如果参与人不能观测到虚拟人——自然的行动, 自然的决策结置于该参与人的前后都一样;
– 自然的信息集总是假定为单结。
N
大 1/2 A
小 1/2 A
开
不
发开
发
B
B
开发
不开发 开发 不开发
– 博弈的战略式表述只包括三个要 素
– 扩展式表述包括以下六个方面的 要素
扩展式表述包括以下六个方面的要素:
– 参与人集合:i=1、2、…,n;并且用大写N代表 虚拟的参与人——“自然”;
– 参与人的行动顺序(The order of moves):谁在什么 时候行动;
– 参与人的行动空间(Action set):在每次行动时, 参与人有些什么选择;
A
坦白 抵赖
B
B
坦白
抵赖
抵赖
坦白
(-8, -8) (0,-10) (-10, 0) (-1,-1)
B
坦白 A
抵赖 A
坦白
抵赖
抵赖
坦白
(-8, -8) (0,-10) (-10, 0) (-1,-1)
(五)完美回忆
完美回忆(Perfect recall)是指没有参与人会 忘记自己以前知道的事情,所有参与人都 知道自己以前的选择。
第三章 完全信息动态博弈
Dynamic Games of Complete Information
@ 2009 Zheng Daowen, All Rights Reserved
动态博弈:参与人的行动有先后顺序,且后 行动者在自己行动之前能观测到先行动者 的行动。
经济博弈论(第三章)
第三章完全信息动态博弈上一章介绍了完全信息静态博弈,本章在前面的基础上探讨完全信息动态博弈。
现实社会经济活动的决策大多数是有先后顺序的行为而不是同时选择的行为,而且后行者能够看到先行者的决策内容,在先行者的决策结果之后再定夺自己的策略。
这样的经济行为比比皆是,如商业活动中的讨价还价,拍卖活动中的轮流竞价,资本市场上的收购兼并和反收购兼并都是如此。
依次选择与一次性同时选择有很大的差异,因此这种决策问题构成的博弈也是从时间序列上有别于静态博弈的,我们称之为“动态博弈”(Dynamic Games)。
例如下象棋通常需要两个参与人,我们定义为红方和黑方,红方先走,黑方后走,这是一个典型的完全信息动态博弈。
动态博弈由于添加了时间因素,因而更加贴近现实。
根据博弈方是否相互了解得益情况,可分为“完全信息动态博弈”和“不完全信息动态博弈”,根据是否所有博弈方都对自己选择前的博弈过程完全了解,可分为“完美信息动态博弈”和“不完美信息动态博弈”。
在本章中,我们首先对博弈的扩展式表达给出完整的定义,为动态博弈的分析奠定基础;其次,我们从扩展式表述博弈的纳什均衡分析逐步深入到子博弈精炼纳什均衡,为动态博弈的分析提供可行的方法,接下来介绍两种完全信息动态博弈经典模型;最后,分析具有无穷次的重复博弈,推导出无名氏定理。
3.1 博弈的扩展式表述在动态博弈中,博弈方的行动是有先后次序的,且后行动者在自己行动之前能够观测到先行动者的行动,每个博弈方的一次选择行为常称为一个“阶段”(Stage )。
动态博弈中也可能存在几个博弈方同时选择的情况,这时博弈方的同时选择构成一个阶段。
一个动态博弈至少有两个阶段,因此动态博弈有时也称为“多阶段博弈”(Multistage Games )。
此外,也有把动态博弈称为“序列博弈”(Sequential Games )的,这也是由动态博弈中的次序特征引出来的。
设有一个商人要从A 地向B 地运输一批货物。
exfd经济博弈论3—完全且完美信息动态博弈
动态博弈中博弈方的策略是他们自己预先设定
的,在各个博弈阶段针对各种情况的相应行为 选择的计划。
这些策略实际上并没有强制力,而且实施起来 有一个过程,因此只要符合博弈方自己的利益, 他们完全可以在博弈过程中改变计划。我们称 这种问题为动态博弈中的“相机选择 (Contingent Play)”。
(-1,0) (0,4)
法律保障不足的开金矿博弈 ——分钱打官司都不可信
稳定。为什么会出现这种情
况呢?
其实,该博弈中 (不借-不打,不分)和(借-打,分)都是纳什
均衡。但后者不可信,不可能实现或稳定。
上述纳什均衡不稳定的原因,主要在于如果甲在第二阶段选择了 “不分”而不是“分”,乙策略中设定的第三阶段“打”是不可 信的,不可能真正实施,理由是该行为对乙自身也是不利的,追 求自身利益最大化的乙的理性不允许他这么做。甲只要稍作分析 就可以掌握乙的这个弱点,因此不可能理睬乙策略中的“打”官 司威胁,在第二阶段不会选择“分”。反过来,乙也不会愚蠢到 想靠一个明显不可信的威胁撑腰,冒险将资金借给甲,因此他在 第一阶段也不可能“借”。
第三章 完全且完美信息动态博弈
本章讨论动态博弈(Dynamic Games),所
有博弈方都对博弈过程和得益完全了解的完全 且完美信息动态博弈。这类博弈也是现实中常
见的基本博弈类型。由于动态博弈中博弈方的 选择、行为有先后次序,因此在表示方法、利 益关系、分析方法和均衡概念等方面,都与静 态博弈有很大区别。本章对动态博弈的概念和 分析方法,特别是子博弈完美均衡和逆推归纳 法作系统介绍,并介绍各种经典的动态博弈模 型。
所以,在一个动态博弈中,博弈的结果包括双
方(或多方)采用的策略组合,实现的博弈路 径和各博弈方的得益。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 为了将“企业2行动时是否知道自己是 在博弈树中的点x2上还是在点x3上”这 一点说清楚,需要引入“信息集”(infor mation set)的概念。
•
在博弈树中,参与人i的一个信息集(用Ii表示) 是参与人i决策结的一个集合,它满足以下两 个条件: (1) Ii中的每个决策结都是参与人i的决策结; (2) 当博弈到达信息集Ii(即博弈到达Ii中某个决策 结)时,参与人i知道自己是在信息集Ii中的决 策结上,但不知道自己究竟在Ii中哪个决策结 上。
• 例子中,用文字描述的方法给出了博弈 问题的扩展式描述。 • 但可以想象,如果我们遇到的是更为复 杂的博弈问题,文字描述可以?
• 十分直观的扩展式博弈的描述方 式——博弈树。
• 所谓博弈树就是由结和有向枝构成的 “有向树”。
企业1的选择 最上端的一个点(用空心圆 有“开发”和 表示),表示博弈的开始 。 “不开发”, 表示博弈达到 分别用标有 该点时企业的 “开发”和 所得 ,其中, “不开发”的 支付向量中的 有向枝表示。 第一个数字表 示企业1的所得, 第二个数字表 示企业2的所 得。
• 也就是说,除了“企业2行动时是否观测 到企业1的选择”这一点,暂时无法从上 图中知道以外,完全信息动态的“新产 品开发博弈”的扩展式描述所需要的信 息(或要素),都可以从上图中得到。
• 如果还能够直接从博弈树中知道“企业2 行动时是否观测到企业1的选择”,那么 给出博弈树,就意味着给出了完全信息 动态的“新产品开发博弈”的扩展式描 述。
第三章 扩展式博弈与完全信 息动态博弈
主要内容: 一、扩展式博弈 二、扩展式博弈的战略及其Nash均衡 三、两种博弈描述形式的比较
一、扩展式博弈
• 所谓扩展式博弈(extensive form game)是 博弈问题的一种规范性描述。与战略式 博弈侧重博弈结果的描述相比,扩展式 博弈更注重对参与人在博弈过程中所遇 到决策问题的序列结构的详细分析。
• 因此,参与人i的信息集Ii可以用来描述: 当轮到参与人i行动时,他所了解到的信 息,即他知道什么(知道自己位于哪一个 信息集上)、不知道什么(不知道自己位于 信息集中哪一个决策结上)。
例如
• 在“新产品开发博弈”中,假设企业1先行动, 企业2后行动,但企业2行动时不知道企业1的 行动。
企业2行动时,只知道 博弈要么到达点x2,要 么达到点x3 ,但具体在 哪一点上,企业2不清 楚。也就是说,企业2 只知道自己位于决策结 集合{x2, x3 }上,但不知 道位于{x2, x3 }中哪一个 决策结上。
将“企业1”标示在点x 1上,表示博弈开始于 企业1的选择。
称为博弈树的结(node) 决策结
回过来再考察上图中的博弈树,可以得到 这样的信息: (1) 博弈中的参与人是企业1和企业2; (2) 博弈中企业1先选择,企业2后选择; (3) 企业1选择时有行动“开发”和“不开 发”,企业2选择的行动有“开发”和 “不开发”; (4) 博弈中企业的支付。
问题:
• 如何在博弈树中,将“企业2行动时 是否观测到企业1的选择”这一信息 表示出来?
•
在完全信息动态的“新产品开发博弈” 中,企业2决策时,企业1已经做出选 择。此时,企业2面临的决策情形就 有以下两种: (1) 企业2知道企业1的选择; (2)业1的选 择,即知道企业1选择了“开发”还是 “不开发”,因此,企业2知道博弈是从 x1到了x2还是从x1到了x3。这就意味着当 轮到企业2决策时,他知道自己是在点x2 上还是在点x3上;
• 设X为一决策结集合,用Ii(X)表示参与人 的由决策结集X构成的一个信息集。 • 例如,I2({x2, x3})表示企业2的由决策结集 {x2, x3}构成的信息集,I2({x2})和I2({x3}) 分别表示企业2的由决策结集{x2}和{x3}构 成的信息集。 • 可以在博弈树中将同一信息集中的决策结 用虚线连接起来。
(4) 两个企业的支付如下:
对手不开发,获利润800万元 需求大 对手开发,获利润300万元 开发(a ):投入2千万元资金 对手不开发,获利润200万元 企业 需求小 对手开发,赔400万元 不开发(b ):不投入资金,利润为0
例子: “新产品开发博弈”
• 试用扩展式博弈对两个企业都知道市场 需求,且企业1先决策,企业2观测到企 业1的选择后再进行选择的博弈情形即完 全信息动态的“新产品开发博弈”进行 建模。
完全信息动态的“新产品开发博弈”的扩 展式博弈包括以下要素: (1) 参与人是企业1和2; (2) 企业1先行动,企业2后行动; (3) 企业1行动时有两种选择——“开发”和 “不开发”,企业1行动时不知道企业2 的行动;企业2行动时有两种选择—— “开发”和“不开发”,但企业2行动时 已经知道企业1的行动;
研究博弈问题的具体进程必须弄清楚的两个问题
(1) 每个参与人在什么时候行动(决策); (2) 每个参与人行动时,他所面临决策问题 的结构。这包括参与人行动时可供他选 择的行动方案,以及参与人行动时所了 解的信息。
扩展式博弈的定义:
扩展式博弈包括以下要素: (1) 参与人集合 {1, 2,..., n} ; (2) 参与人的行动顺序,即每个参与人在何时行 动; (3) 每个参与人行动时面临的决策问题,包括参 与人行动时可供他选择的行动方案以及他所 了解的信息; (4) 参与人的支付函数,即博弈结束时每个参与 人得到的博弈结果。
• 对于第二种情形,企业2不知道企业1的 选择,即不知道博弈是从x1到了x2还是从 x1到了x3。因此,当轮到企业2决策时, 他不知道自己是在点x2上还是在点x3上。 所以,“企业2行动时是否观测到企业1 的选择”这一问题,实际上就等价于 “企业2行动时是否知道自己是在博弈树 中的点x2上还是在点x3上”。
