固支梁各阶固有频率及振型测量
连续弹性体悬臂梁各阶固有频率及主振型测定(最全)word资料
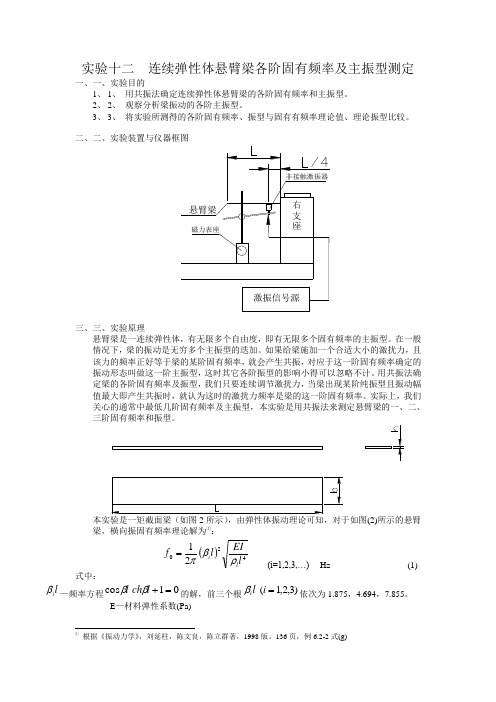
实验十二 连续弹性体悬臂梁各阶固有频率及主振型测定一、一、实验目的1、 1、 用共振法确定连续弹性体悬臂梁的各阶固有频率和主振型。
2、 2、 观察分析梁振动的各阶主振型。
情况下,梁的振动是无穷多个主振型的迭加。
如果给梁施加一个合适大小的激扰力,且该力的频率正好等于梁的某阶固有频率,就会产生共振,对应于这一阶固有频率确定的振动形态叫做这一阶主振型,这时其它各阶振型的影响小得可以忽略不计。
用共振法确定梁的各阶固有频率及振型,我们只要连续调节激扰力,当梁出现某阶纯振型且振动幅值最大即产生共振时,就认为这时的激扰力频率是梁的这一阶固有频率。
实际上,我们关心的通常中最低几阶固有频率及主振型,本实验是用共振法来测定悬臂梁的一、二、l i β①根据《振动力学》,刘延柱,陈文良,陈立群著,1998版。
136页,例6.2-2式(g)A — A — 梁横截面积(m 2)l ρ—材料线密度(kg/m) l ρ=ρAρ—材料密度(kg/m 3) I —梁截面弯曲惯性矩(m 4)对矩形截面,弯曲惯性矩:123bhI = (m 4) (2)式中: b —梁横截面宽度(m) h —梁横截面高度(m) 本实验取l =( ) m b=( ) m h=( ) mE=20×1011Pa ρ=7800kg/m 3 各阶固有频率之比:f 1:f 2:f 3:f 4……=1:6.27:17.55 (3)理论计算可得悬臂梁的一、二、三阶固有频率的振型如图(3)所示:0.10.20.30.40.50.60.70.80.91-10120 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1-2020 0.10.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 10.511.5beam transvers vibration with one end clasped四、四、实验方法1、 1、 选距固定端L/4之处为激振点,将激振器端面对准悬臂梁上的激振点,保持初始间隙δ=6~8mm 。
振动系统各阶固有频率及模态测试探究性实验设计

振动系统各阶固有频率及模态测试探究性实验设计1. 引言1.1 引言振动系统是指具有振动特性的物体或系统,它们会在外力作用下发生振动。
振动系统的研究对于理解和分析各种物体或结构的振动行为具有重要意义。
在实际工程中,振动系统的研究和分析通常会涉及到固有频率和模态测试。
固有频率是指一个振动系统在没有外力作用下自发振动的频率。
固有频率的大小与系统的质量、刚度和阻尼等因素有关,它反映了系统振动的特性和稳定性。
固有频率的测定对于系统的性能分析和设计优化具有重要意义。
模态测试是一种用于测定振动系统各阶固有频率和振动模态的方法。
通过模态测试可以获得系统各个振动模态的振幅、相位和频率等信息,从而帮助分析系统的振动特性和优化设计。
本实验旨在探究振动系统各阶固有频率及模态的测试方法和实验设计。
通过实验可以深入理解振动系统的工作原理和特点,为实际工程应用提供参考。
在本文中,将介绍振动系统的概念和特点、固有频率的含义和重要性、模态测试的意义和方法、实验设计的步骤和要点以及实验结果分析与讨论,旨在全面了解振动系统的性能和优化方法。
2. 正文2.1 振动系统的概念和特点振动系统是由质量、弹簧和阻尼器构成的物理系统,当外力作用于系统时,系统会发生振动。
振动系统具有以下特点:振动系统具有固有频率,即系统在没有外力作用下的自然频率,这取决于系统的质量和弹性系数;振动系统可能出现共振现象,即在外力频率接近系统的固有频率时,系统会受到更大的振幅影响;振动系统具有不同的模态,即系统在不同方式振动时呈现不同的振动模式。
振动系统的概念和特点对于工程领域具有重要意义。
通过对振动系统的研究,可以更好地了解系统的动态特性,预测系统的振动响应,并设计有效的振动控制措施。
振动系统的特点也直接影响到系统的性能和稳定性,在工程实践中需要认真考虑和分析。
在进行振动系统的实验设计时,需要充分考虑系统的特点,合理选择实验方法和参数,以获取准确和可靠的实验数据。
振动系统固有频率的测试

振动系统固有频率的测试实验指导书一.实验目的1.学习振动系统固有频率的测试方法;2.了解DASP-STD软件;3.学习锤击法测试振动系统固有频率的原理与方法;(传函判别法)二.实验仪器及简介ZJY-601T型振动教学实验台,ZJY-601T型振动教学试验仪,采集仪,DASP-STD(DASP Standard 标准版)软件,微机。
1.ZJY-601T型振动教学实验台:主要由底座、桥墩型支座、简支梁、悬臂梁、等强度梁、偏心电动机、调压器、接触式激振器及支座、非接触式激振器、磁性表座、减振橡胶垫、减振器、吸振器、悬索轴承装置、配重锤、钢丝、圆板、质量块等部件和辅助件组成。
与ZJY-601T型振动教学实验仪配套,完成各种振动教学实验。
它以力学和电学参数为设计出发点,力学模型合理,带有10种典型力学结构,多种激振、减振和拾振方式。
力学结构有:两端简支梁、两端固支梁、等截面悬臂梁、等强度悬臂梁(变截面)、复合材料梁、圆板、单自由度质量-弹簧系统、两自由度质量-弹簧系统、三自由度质量-弹簧系统、悬索。
激励方式有:脉冲锤击法、正弦激励(接触、非接触式)、正弦扫描(接触、非接触式)、偏心质量、支承运动。
减振和隔振有:主动隔振、被动隔振、阻尼减振、动力减振(单式)、动力减振(复式)。
传感器类型有:压电加速度传感器、磁电式速度传感器、电涡流位移传感器、力传感器(力锤中)。
2.ZJY-601T型振动教学试验仪:由双通多功能振动测试仪、扫频信号发生器、功率放大器组成,并集成了数据采集器,可连接压电式加速度传感器、磁电式速度传感器或电涡流传感器,对被测物体的振动加速度、速度和位移进行测量。
可将每个通道所测振动信号转换成与之相对应的0~5V AC电压信号输出,供计算机使用。
扫频信号发生器的输出频率在手动档时,可通过旋钮在0.1~1000Hz范围内连续调节;在自动档时,可从10到1000Hz自动变换,扫频时间可由电位器控制,3s~240s连续可调,激振频率可由液晶显示器显示。
振动系统固有频率的测试

检测Байду номын сангаас果
每个测试项目的检测结果都分别进行了三次击锤, 取三次采集数据的平均值:垂直方向击锤检测的固 有频率值为45.04Hz;横向方向检测的固有频率值 为44.68Hz。
以上介绍了我公司的产品试验室对汽车零部件进行 固有频率检测的基本过程,没有对检测结果的具体 数据做进一步研究讨论,目的是让读者对汽车NVH 问题分析有初步的了解。
一、实验目的 二、实验装置 三、实验原理 四、实验步骤 五、实验结果
目录
实验目的
1. 学习振动系统固有频率的测试方法;
2. 学习共振动法测试振动固有频率的原理与方法;(幅值判 别法和相位判别法)
3.学习衰减振动波形自谱分析法测试振动系统固有频率的原 理和方法。(自谱分析法)
物体作自由振动时,其位移随时间按正弦规律变化,又称为 简谐振动。简谐振动的振幅及初相位与振动的初始条件有关, 振动的周期或频率与初始条件无关,而与系统的固有特性有 关,称为固有频率或者固有周期。 物体频率与它的硬度、质 量、外形尺寸有关,当其发生形变时,弹力使其恢复。弹力 主要与尺寸和硬度有关,质量影响其加速度。同样外形时, 硬度高的频率高,质量大的频率低。
3.锤击操作 (1)锤击点:在转向管柱的下端选择锤击点。 (2)锤击方向:设垂击方向为垂直,并通过转向管柱的转向轴中心线。 (3)锤击方式:手握击锤分别对检测件进行横向和垂直两个方向的击打。 击锤操作的质量好坏直接关系到整个测试数据的准确性和可靠性。由于击锤操作主要
双简支梁固有频率及振型测量

《振动测试实验》实验报告∗南京航空航天大学机械结构力学及控制国家重点实验室二○一一年∗注:实验报告完成后请以附件形式发送至:wt78@邮件主题请写明:《振动测试实验报告》,姓名,学号,分班号(三班或四班)一、实验目的•测量双简支梁的固有频率和振型。
•理解多自由度系统振型的物理概念。
•掌握多自由度系统固有频率和振型的简单测量方法。
二、实验原理图简支梁固有频率和振型测试原理图三、实验过程1、将功率放大器“输出调节”旋至最小,“信号选择”置“外接”。
打开各设备电源。
2、进入“双简支梁固有频率与振型测量”实验操作界面,使信号发生器的输出频率约为 30Hz,输出电压约为 1V 。
调节功率放的“输出调节”,逐渐增大其输出功率直至质量块有明显的振动(观察并用手触摸)。
3、将信号发生器输出频率由低向高逐步调节,同时观察李萨育图形。
当李萨育图为稳定的正椭圆时,信号发生器的频率读数即为第一阶固有频率。
继续将信号发生器的频率向高逐步调节,测出第二阶、第三阶固有频率。
4、再将信号发生器调到第一阶固有频率值,保持功率放大器的输出功率恒定(即:不再改变信号发生器的输出电压和功率放大器的输出功率),保持“参考”传感器的位置不变。
将“测量”传感器从双简支梁的右端等距跑点,依次记下“测量”传感器在各个位置时的测量点与参考点传感器输出电压之比(即“测量点/参考点”的显示值)及其正负号。
将其归一化即可得到第一阶振型,填“振型数据”表格。
点击“振型图”或“振型动画”检验振型数据。
四、实验数据与分析1、列出固有频率。
双简支梁的3个阶段的固有频率分别为:一阶: 36.7Hz二阶: 136.5Hz三阶: 326.6Hz一阶振型图二阶振型图3、测量双简单支梁振型时,改变“测量”传感器位置后,李萨育图形出现非正椭圆,解释原因,如何避免?答:测量双简单支梁振型时,改变“测量”传感器位置后,由于传感器有一定的质量,改变传感器位置也就改变了系统的质量分布,必然引起其固有频率的变化,在李萨育图形上表现出呈非正椭圆。
振动系统固有频率的测试实验原理、方法和报告

振动系统固有频率的测试一、实验目的1、学习振动系统固有频率的测试方法;2、学习共振动法测试振动固有频率的原理与方法二、实验装置简图图2-11、简支梁2、加速度传感器3、接触式激振器三、实验仪器简介请参照实验一《简谐振动幅值测量》内介绍。
四、实验原理1、幅值判别法在激振功率输出不变的情况下,由低到高调节激振器的激振频率,通过示波器可以观察到在某一频率下,任一振动量(位移、速度、加速度)幅值迅速增加,这就是机械振动系统的某阶固有频率。
这种方法简单易行,但在阻尼较大的情况下,不同的测量方法得出的共振频率稍有差别,不同类型的振动量对振幅变化敏感程度不一样,这样对于一种类型的传感器在某阶频率时不够敏感。
2、相位判别法相位判别法时根据共振时特殊的相位值以及共振前后相位变化规律所提出来的一种共振判别法。
在简谐力激振的情况下,用相位法来判定共振是一种较为敏感的方法,而且共振时的频率就是系统的无阻尼固有频率,可以排除阻尼因素的影响。
激振信号为:F=F sinωt位移信号为:x=x0sin(ωt+φ)速度信号为:v=ωx0cos(ωt+φ)加速度信号为:a=-ω2x0sin(ωt+φ)1)位移判别共振将激振信号输入到采集仪的第一通道(即X轴),位移传感器输出信号或通过振教仪积分档输出量为位移的信号输入到第二通道(即Y轴),此时两通道的信号分别为:激振信号为:F=F sinωt位移信号为:x=x0sin(ωt+φ)共振时,ω=ωn,φ=π/2,X轴信号和Y轴信号的相位差为π/2,根据莉萨如图原理可知,屏幕上的图形将是一个正椭圆。
当ω略大于ωn或略小于ωn时,图像都将由正椭圆变为斜椭圆,其变化过程如图2-2所示。
因此图像由斜椭圆变为正椭圆的频率就是振动体的固有频率。
ω<ωnω=ωnω>ωn图2-2用位移判别共振的莉萨如图形2)速度判别共振将激振信号输入到采集仪的第一通道,速度传感器输出信号或通过振教仪积分档输出量为速度的信号输入到第二通道(即Y轴),此时两通道的信号分别为:激振信号为:F=F sinωt速度信号为:v=ωx0cos(ωt+φ)共振时,ω=ωn,φ=π/2,X轴信号和Y轴信号的相位差为π/2,根据莉萨如图原理可知,屏幕上的图形将是一条直线。
实验五简支梁固有频率测试实验1

实验五 简支梁固有频率测试实验一、 实验目的:1、 掌握固有频率测试的工程意义及测试方法。
2、 掌握用共振法、李萨育图形法测量振动系统的固有频率的方法及步骤。
3、 加深了解常用简单振动测试仪器的使用方法。
二、实验设备和工具1.机械振动综合实验装置(安装简支梁) 1套2.激振器及功率放大器 1套3.加速度传感器 1台4.电荷放大器 1台5.数据采集仪 1台6.信号分析软件 1套三、实验内容1.用共振法测量简支梁固有频率共振法测量振动系统的固有频率是比较常用的方法之一。
共振是指当激振频率达到某一特定值时,振动量的振动幅值达到极大值的现象。
由弹性体振动理论可知,计算简支梁固有频率理论解为:APEJ L f 20115.49 式中,L 为简支梁长度(cm );E 为材料弹性系数(kg/cm 2);A 为梁横截面积(cm 2);P 为材料比重(kg/cm 3);J 为梁截面弯曲惯性矩(cm 4)。
用共振法测量简支梁固有频率的仪器连接如图1所示图1测量双简支梁固有频率框图2.用李萨育图形法测量简支梁固有频率李萨育图形是由运动方向相互垂直的两个简谐振动的合成运动轨迹。
李萨育图形可以通过示波器或数据采集软件的X-Y轨迹图观察到。
在图的X、Y 轴上同时输入简谐振动两个信号,这两个信号不同的相位差合成不同的李萨育图形如图2所示。
振动的位移、速度及加速度的幅值其各自达到极大值时频率是不同的,只有在无阻尼的情况下,它们频率才相等,并且等于振动系统的固有频率。
但在弱阻尼的情况下,三种共振频率接近系统的固有频率。
只有速度共振频率真正和固有频率相等,所以用速度共振的相位差判别共振。
判别依据是系统发生速度共振时,激振力和速度响应之间的相位差为90°,依据位移、速度、加速度响应判断速度共振的李萨育图形如图3~5所示。
θ=00 θ=450 θ=900 θ=1350 θ=1800图2 不同相位差信号合成的李萨育图形n ωω< n ωω= n ωω>图3用位移响应判断速度共振n ωω< n ωω= n ωω>图4用速度响应判断速度共振n ωω< n ωω= n ωω>图5用加速度响应判断速度共振四、实验原理固有频率是振动系统的一项重要参数。
测试梁的各阶固有频率试验

21
梁的横向振动微分方程
图中的直梁在xy平面内作横向振动。假定梁的各截面 的中心惯性主轴在同一平面Oxy内,外载荷也作用在该平 面,并且略去剪切变形的影响及截面绕中性轴转动惯量的 影响,因此梁的主要变形是弯曲变形,这即是通常称为欧 拉-伯努利梁的模型。
22
•
在梁上x处取长为dx的微元段。在任意瞬时t,此微元 段的横向位移用y(x, t)表示;单位长度梁上分布的外力用 p (x, t)表示;单位长度梁上分布的外力矩用m (x, t)表示。记 梁的密度为 ,横截面积为A,材料弹性模量为E,截面 对中性轴的惯性矩为J。由牛顿第二定律写出微段沿y向的 运动微分方程
如果函数f(t)的周期T无限增大,则f(t)成为非周期函 数。傅氏积分和傅氏变换是研究非周期函数的有力手段。 与周期函数不同,非周期函数的频谱是连续曲线。 由数学知,若非周期函数f(t)满足条件:(1) 在任一 有限区间满足狄氏条件;(2) 在区间 (-,+) 上绝对 可积,则在f(t)的连续点处有 1 jt jt f (t ) [ f ( t ) e dt ] e d (4) 2 上式称函数 f (t ) 的傅氏积分公式。如令
k
fn
F
1 2 k m
3
4-1-5 用“三线摆”法验证均质圆盘转动惯量理论公式 实验目的 1. 了解并掌握用“三线摆”方法测取物体转动惯量的方 法。 2. 分析“三线摆”摆长对测量的误差。 “三线摆”是测取转动惯量的一种常用方 法。给摆一个微小偏转,然后自然释放,摆 就会产生扭振。同样的摆线长,不同的转动 惯量,摆动的周期是不相同的;而同样的转 动惯量,不同的摆长,摆动的周期也不相同。 因此,“三线摆”的摆动周期不仅与物体的 转动惯量有关,而且与摆线的长度也有关。 根据摆的线长和摆动周期,可以推算出三线 o 摆在线性振动范围内圆盘转动惯量计算公式 为 mgr 2T 2 Jc 4 三线摆示意图 4 2l
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
固支梁各阶固有频率及振型测量
一、实验目的:
1. 熟悉梁的固有频率测量原理及振型形状;
2. 用共振法确定固支梁的各阶固有频率和振型。
二、实验仪器设备及安装示意图:
1. 计算机
2. YE6230T3动态数据采集系统
3. 功率函数发生器
4. 机械振动实验台
5. 加速度传感器激光位移传感器电涡流传感器自选
6. 激振器
三、实验过程:
四、实验结果及分析:
1、前三阶固有频率测量结果
2、各测点实测振幅(单位:)1,175;
3、各测点振幅换算值
4、绘出固支梁前三阶振型图一阶振型图
二阶振型图三阶振型图
多自由度系统各阶固有频率及主振型的测量一、实验目的
二、实验设备及安装示意图
三、实验结果与分析
1、不同张力下各阶固有频率的理论计算值与实测值
2、绘出观察到的三自由度系统振型曲线。
3、将理论计算出的各阶固有频率、理论振型与实测固有频率、实测振型相比较,是否一致? 产生误差的原因在哪里?。
