七年级数学变量之间的关系[人教版]
七年级数学下册第三章变量之间的关系知识归纳

第三章变量之间的关系自变量变量的概念因变量变量之间的关系表格法关系式法变量的表达方法速度时间图象图象法路程时间图象一、变量、自变量、因变量1、在某一变化过程中,不断变化的量叫做变量。
2、如果一个变量y随另一个变量x的变化而变化,则把x叫做自变量,y叫做因变量。
3、自变量与因变量的确定:(1)自变量是先发生变化的量;因变量是后发生变化的量.(2)自变量是主动发生变化的量,因变量是随着自变量的变化而发生变化的量。
(3)利用具体情境来体会两者的依存关系。
二、表格1、表格是表达、反映数据的一种重要形式,从中获取信息、研究不同量之间的关系。
(1)首先要明确表格中所列的是哪两个量;(2)分清哪一个量为自变量,哪一个量为因变量;(3)结合实际情境理解它们之间的关系。
2、绘制表格表示两个变量之间关系(1)列表时首先要确定各行、各列的栏目;(2)一般有两行,第一行表示自变量,第二行表示因变量; (3)写出栏目名称,有时还根据问题内容写上单位;(4)在第一行列出自变量的各个变化取值;第二行对应列出因变量的各个变化取值.(5)一般情况下,自变量的取值从左到右应按由小到大的顺序排列,这样便于反映因变量与自变量之间的关系。
三、关系式1、用关系式表示因变量与自变量之间的关系时,通常是用含有自变量(用字母表示)的代数式表示因变量(也用字母表示),这样的数学式子(等式)叫做关系式。
2、关系式的写法不同于方程,必须将因变量单独写在等号的左边。
3、求两个变量之间关系式的途径:(1)将自变量和因变量看作两个未知数,根据题意列出关于未知数的方程,并最终写成关系式的形式.(2)根据表格中所列的数据写出变量之间的关系式;(3)根据实际问题中的基本数量关系写出变量之间的关系式;(4)根据图象写出与之对应的变量之间的关系式。
4、关系式的应用:(1)利用关系式能根据任何一个自变量的值求出相应的因变量的值;(2)同样也可以根据任何一个因变量的值求出相应的自变量的值;(3)根据关系式求值的实质就是解一元一次方程(求自变量的值)或求代数式的值(求因变量的值)。
数学七年级下册知识点总结之变量之间的关系

数学七年级下册知识点总结之变量之间的关系变量之间的关系知识点:一理论理解1、若Y随X的变化而变化,则X是自变量 Y是因变量。
自变量是主动发生变化的量,因变量是随着自变量的变化而发生变化的量,数值保持不变的量叫做常量。
2、能确定变量之间的关系式:相关公式①路程=速度时间②长方形周长=2(长+宽)③梯形面积=(上底+下底)高2 ④本息和=本金+利率本金时间。
⑤总价=单价总量。
⑥平均速度=总路程总时间3、若等腰三角形顶角是y,底角是x,那么y与x的关系式为y=180-2x.二、列表法:采用数表相结合的形式,运用表格可以表示两个变量之间的关系。
列表时要选取能代表自变量的一些数据,并按从小到大的顺序列出,再分别求出因变量的对应值。
列表法最大的特点是直观,可以直接从表中找出自变量与因变量的对应值,但缺点是具有局限性,只能表示因变量的一部分。
三.关系式法:关系式是利用数学式子来表示变量之间关系的等式,利用关系式,可以根据任何一个自变量的值求出相应的因变量的值,也可以已知因变量的值求出相应的自变量的值。
四、图像注意:a.认真理解图象的含义,注意选择一个能反映题意的图象;b.从横轴和纵轴的实际意义理解图象上特殊点的含义(坐标),特别是图像的起点、拐点、交点八、事物变化趋势的描述:对事物变化趋势的描述一般有两种:1.随着自变量x的逐渐增加(大),因变量y逐渐增加(大)(或者用函数语言描述也可:因变量y随着自变量x的增加(大)而增加(大));2. 随着自变量x的逐渐增加(大),因变量y逐渐减小(或者用函数语言描述也可:因变量y随着自变量x的增加(大)而减小).注意:如果在整个过程中事物的变化趋势不一样,可以采用分段描述.例如在什么范围内随着自变量x的逐渐增加(大),因变量y逐渐增加(大)等等.九、估计(或者估算) 对事物的估计(或者估算)有三种:1.利用事物的变化规律进行估计(或者估算).例如:自变量x每增加一定量,因变量y的变化情况;平均每次(年)的变化情况(平均每次的变化量=(尾数-首数)/次数或相差年数)等等;2.利用图象:首先根据若干个对应组值,作出相应的图象,再在图象上找到对应的点对应的因变量y的值;3.利用关系式:首先求出关系式,然后直接代入求值即可.拓展:数学学习技巧一、课内重视听讲,课后及时复习。
七年级数学专项习题——变量之间的关系(附参考答案)
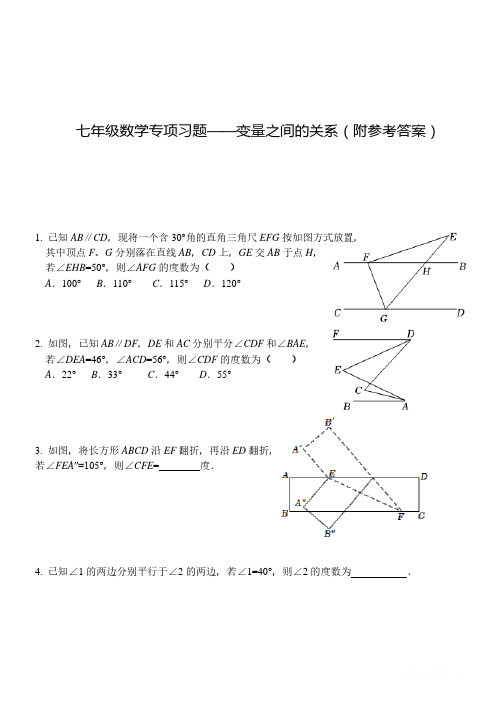
1. 已知AB ∥CD ,现将一个含30°角的直角三角尺EFG 七年级数学专项习题——变量之间的关系(附参考答案)按如图方式放置,其中顶点F 、G 分别落在直线AB ,CD 上,GE 交AB 于点H ,若∠EHB =50°,则∠AFG 的度数为( )A .100°B .110°C .115°D .120°2. 如图,已知AB ∥DF ,DE 和AC 分别平分∠CDF 和∠BAE ,若∠DEA =46°,∠ACD =56°,则∠CDF 的度数为( )A .22°B .33°C .44°D .55°3. 如图,将长方形ABCD 沿EF 翻折,再沿ED 翻折,若∠FEA ″=105°,则∠CFE = 度.4. 已知∠1的两边分别平行于∠2的两边,若∠1=40°,则∠2的度数为 .5. 如图,将一副三角板的直角顶点重合,摆放在桌面上,当∠AOC= 时,AB所在直线与CD所在直线互相垂直.6. 已知:如图△ABC中,AC⊥BC,点D、E在AB边上,点F在AC边上,DG⊥BC于G,∠1=∠2.求证:EF∥CD.(请在下面空白处写出完整证明过程)∴∠AHG =∠EHB =50°,∵AB ∥CD ,∴∠EGD =∠AHG =50°,∵∠FGE =60°,∴∠FGD =∠FGE +∠EGD =60°+50°=110°,∵AB ∥CD ,∴∠AFG =∠FGD =110°1.解:∵GE 交AB 于点H 参考答案,.故选:B .2.解:过点C 作CN ∥AB ,过点E 作EM ∥AB ,∵FD ∥AB ,CN ∥AB ,EM ∥AB ,∴AB ∥CN ∥EM ∥FD∴∠BAC =∠NCA ,∠NCD =∠FDC ,∠FDE =∠DEM ,∠MEA =∠EAB . ∴∠DEA =∠FDE +∠EAB ,∠ACD =∠BAC +∠FDC .又∵DE 和AC 分别平分∠CDF 和∠BAE ,∴∠FDC =2∠FDE =2∠EDC ,∠BAE =2∠BAC =2∠EAC , ∴56°=∠BAC +2∠FDE ①,46°=∠FDE +2∠BAC ②.①+②,得3(∠BAC +∠FDE )=102°,∴∠BAC +∠FDE =34°③.①-③,得∠FDE =22°.∴∠CDF =2∠FDE =44°.故选:C .3.解:由四边形ABFE 沿EF 折叠得四边形A ′B ′FE ,∴∠A ′EF =∠AEF .∵∠A ′EF =∠A ′ED +∠DEF ,∠AEF =180°-∠DEF .∴∠A ′ED +∠DEF =180°-∠DEF .由四边形A ′B ′ME 沿AD 折叠得四边形A ″B ″ME ,∴∠A ′ED =∠A ″ED .∵∠A ″ED =∠A ″EF +∠DEF =105°+∠DEF ,∴∠A ′ED =105°+∠DEF .∴105°+∠DEF +∠DEF =180°-∠DEF .∴∠DEF =25°.∵AD ∥BC ,∴∠DEF =∠EFB =25°.∴∠CFE =180°-∠EFB =180°-25°=155°.故答案为:155.4. 解:①若∠1与∠2位置如图1所示:∵AB ∥DE ,∴∠1=∠3, 又∵DC ∥EF ,∴∠2=∠3,∴∠1=∠2,又∵∠1=40°,∴∠②若∠1与∠2位置如图2所示:∵AB∥DE,∴∠1=∠3,又∵DC∥EF,∴∠2+∠3=180°,∴∠2+∠1=180°,又∵∠1=40°,∴∠2=180°-∠1=180°-40°=140°,综合所述:∠2的度数为40°或140°,故答案为:40°或140°.5.6. 证明:,,( 已知 ),( 垂直的定义 ),( 同位角相等,两直线平行)两直线平行,内错角相等),( 已知 ),( 等量代换 )同位角相等,两直线平行)。
七年级数学变量之间的关系

。 职业考试培训 /
我的院子在市郊乌拉街,有38公里那么远。往返其间的大巴车平均20分钟一趟。我坐在车上,想我家的老院子,已经盛装好了满满一院子的雪,在等待着我,提出修改意见。
车窗外,漫山遍野,都是白色的了。
老家最大的一场雪,是在我七八岁的时候下的。那么大的雪,不可能白天下。老天爷也知道黑夜下雪是不对的,但那天老天爷就想这么任性一下子,并且没控制住自己的任性,结果那场我此生经历 过的最大的雪,就下来了。那是一个特别平常的夜晚。所有人在天黑之后都睡觉了。天上主管下雪的那位神仙,等所有人都睡了之后,看见地上的灯火都熄灭了之后,就把怀里抱着的大雪团扔了下来。 再大的雪,也没有一丝声响,像一只蹑手蹑脚的白猫跳上了我家的房顶。像无数只蹑手蹑脚的白猫,跳上了所有人家的房顶。雪神忙了一晚上,凌晨的时候,看看下面的房子只剩下了房脊,他开心地笑 了,拍了拍手,回去休息了。
第二天早上,并不是推门一看:啊,山上白了,地上白了,房子上白了,树上白了,这样的平庸之作,而是根本推不开门。房门被雪堵住了。这就不是作品了,而是恶作剧;这就不是瑞雪了,而是 雪灾。瑞雪要适量,不多不少,正正好好。
后来,大家都从被封住的房子里出来了。一般是家里最身强力壮的那个人,用个人才能走出去,把门后的雪推到一边。听说还有 的人家,因为房子太矮,多半个门都盖住了,从里面推不开,一条缝也推不开,只好由窗子出来。
初中数学《变量之间的关系》单元教学设计以及思维导图

学习函数图像奠定了基础。 本专题的重点是理解用图像表示两个变量之间的关系
本专题的主要学习活动是利用图像法解决一些实际问题。
学生的主要学习成果:
能够从图象中分析变量之间的关系,明确图象上点所表示的意义,会
利用图象找到准确的信息。
专题学习目标
知识技能:
1.培养学生的观察能力,根据图像预测能力,分析能力,动手操作
(1)这个变化过程中,自变量、因变量各是什么? (2)如果三角形的底边长为 x(厘米),那么三角形的面积 y(厘米 2) 可以表示为 ________________。 (3) 当底边长从 12 厘米变化到 3 厘米时,三角形的面积从_____平 方厘米变化到_____平方厘米. 活动 3:(1)同学们能根据要求填写下列的表格吗? 根据三角形的底边长为 x(厘米),和三角形的面积 y(厘米 2)的 关系式填表:
量间的关系判断和识别图像。
主 题 单 元 问 1. 举例说明自变量和因变量,常量。
题设计
2. 表示变量之间关系的方法有哪些,各有什么特点?
专题一:用表格表示变量之间的关系
( 1 课时)
专题划分
专题二:用关系式表示变量之间的关系 ( 1 课时)
专题三: 用图像表示变量之间的关系
( 2 课时)
专题一
用表格表示变量之间的关系
专题二
用关系式表示变量之间的关系
所需课时 课内 1 课时 专题二概述
本专题内容是建立在学生已理解变量、自变量、因变量的意义和体会 到了因变量是随自变量变化而变化的基础上,教材通过对三角形的底
边的变化引起三角形面积的变化问题的探索,探索出了变量间的变化
规律可用关系式来表达,运用表达式可以描述出自变量和因变量具体 变化的情况。
七年级下变量关系知识点

七年级下变量关系知识点变量关系是初中数学的重要基础知识之一,包括正比例关系、反比例关系和其他变量之间的关系。
七年级下学期,在学习代数之前,我们需要掌握一些基本的变量关系知识点。
一、正比例关系正比例关系是指两个变量之间的关系呈现一定的比例关系,即其中一个变量的值是另一个变量的某个倍数。
例如,当小明每天学习1小时时,他每天进步10分;每天学习两小时时,他每天进步20分。
这里学习时间与进步分数的关系呈现出正比例关系,即每小时学习可以进步10分。
正比例关系可以用数学公式表示为y=kx,其中x和y分别表示两个变量,k表示比例常数。
在上述例子中,进步分数y就是学习时间x的10倍,即y=10x。
二、反比例关系反比例关系是指两个变量之间的关系呈现出等比例关系,即一个变量的增加导致另一个变量的减少,两者之间的乘积保持不变。
例如,当一辆车的速度增加时,它需要的时间减少;而当速度减慢时,所需时间增加。
这里速度与时间的关系呈现出反比例关系。
反比例关系可以用数学公式表示为y=k/x。
在上述例子中,所需时间y是车速度x的倒数,即y=k/x。
三、变量之间的其他关系除了正比例关系和反比例关系,变量之间还可能存在其他的复杂关系。
例如,小明每天自行车骑行一小时,他在一天能吃下3000卡路里;如果他骑行两个小时,他能吃下6000卡路里。
这里骑行时间与卡路里的摄入量之间呈现出无规律的关系。
在实际问题中,变量之间的关系并不一定呈现出简单的比例关系。
我们需要通过逐步探究与分析,寻找变量之间的规律关系,从而归纳总结出一定的函数关系。
总结七年级下一些基本的变量关系知识点包括正比例关系、反比例关系和其他变量之间的关系。
这些知识点是进一步学习函数的基础,也是实际问题中解决数量关系问题的基础。
通过多做例题,我们可以更加深入地理解变量关系,并应用于实际问题中。
七年级数学下册第三章变量之间的关系2用关系式表示的变量间关系1

12/10/2021
第十二页,共二十九页。
2. 将长为40 cm,宽为15 cm的长方形白纸,按图3-2-4所示 的方法粘合起来,粘合部分宽为5 cm.
(1)根据图,将下表格(biǎogé)补充完整.
白纸(bái zhǐ)张数/张1
所以汽车行驶600 km时剩油8 L.
12/10/2021
第九页,共二十九页。
模拟演练
1. 用一根长是20cm的细绳围成一个长方形 (如图3-2-
3),这个长方形的一边的长为xcm,它的面积(miàn 为 jī) ycm2.
(1) 写出y与x之间的关系式,在这个
关系式中,哪个是自变量?它的取值应
在什么范围内?
第三章 变量 之间的关系 (biànliàng)
2 用关系式表示的变量(biànliàng)间关系
12/10/2021
第一页,共二十九页。
课前预习
1. 变量(biànliàng)x与y之间的关系是y= x2-3,当自变量x=2时,
因变量y的值是 A. -2
B. -1
() B
C. 1
D. 2
12/10/2021
解得x=90.
答:小丽家4月份用煤气90 m3.
12/10/2021
第二十六页,共二十九页。
(4)设6月份(yuèfèn)小丽家用了a m3的煤气. 根据题意,得1.2a-20=0.95a. 解得a=80.
答:6月份小丽家用了80 m3的煤气.
12/10/2021
第二十七页,共二十九页。
12/10/2021
(km)和所用时间t (h) 用关系式可表示为_______.
七年级变量间的关系知识点

七年级变量间的关系知识点在七年级数学学习中,变量是一个重要的概念。
变量是可以赋值而不是具体的数字或者对象,因此它可以用来表示一组不同的数值或者自然语言中的实体。
在本篇文章中,我们将会详细讨论七年级中变量间的关系知识点。
一、变量的定义和使用在代数表达式中,我们通常使用字母来表示一个变量。
这个变量可以代表任意实数,我们可以将其赋值为特定的数字或表达式,来求得代数式的值。
例如:设 a = 2,则 a + 3 = 5b = 4,则 b - 1 = 3我们用变量来存储一组数字,这些数字可以是实数、整数、分数等。
通过变量的方式,我们可以轻松地对表达式进行变化和操作,大大方便了数学问题的解决。
二、变量间的关系1. 变量的相等关系在使用变量的时候,我们经常会碰到一些等式。
比如:2x + 1 = 5y - 3 = 2这里的“=”代表两边的值相等。
这种关系被称为“等式”。
在等式中,我们可以将其中一个变量用另一个变量表示出来,从而建立两个变量之间的关系。
例如:2x + 1 = 52x = 4x = 2由此可见,不同变量之间可以建立相等和不等的关系。
2. 变量的大于小于关系有时候我们需要判断两个变量之间的大小关系。
比如:3x + 2 > 5x - 1y + 4 < 2y - 3这里的“>”和“<”分别代表“大于”和“小于”,用于判断两个变量之间的大小关系。
我们可以通过移项、合并同类项、化简等方法,将不等式变形为关于变量的简单形式。
3x + 2 > 5x - 1-2x > -3x < 3/23. 变量之间的比例关系变量之间的比例关系在我们的日常生活中也经常出现。
比如:小明比小红高出 10 厘米,小明的身高是小红身高的 1.2 倍。
这里的“高出”“身高”“倍数”等词汇涉及到了变量之间的比例关系。
我们可以通过设置比例、计算比例中的变量,来解决涉及到变量间的比例关系的问题。
小明比小红高出 10 厘米,小明的身高是小红身高的 1.2 倍。
