阶跃信号
阶跃信号和冲激信号

3) 奇偶性:
(t) (t) (t) (t) (n) (t) (1)(n) (n) (t)
由第四组a=-1得来 由第五组a=-1得来
结论: 冲激函数为偶函数 冲激偶函数为奇函数
n为偶数时, (n) (t) 为偶函数, n为奇数时, (n) (t) 为奇函数
例题
例题1-3-2
1.计 算 : (2 cos3t) ( t )dt
(n)(t t0 ) d t
(1)n
f
(n) (t0 )例题 Nhomakorabea例 (题t) f1(-t)d3-t 1f (0)
f (t) (t) d t f (0)
1.计 算 : (2t sin 2t) (t)dt
2.练 习 :
[2t 2 cos (t 1)] (t 2)dt
3
2 1
2 (t) sin 2t dt
第五组: (at) 1 1 (t)
aa
(n) (at )
1 a
1 an
(n) (t )
*第六组:
(at
t0 )
a(t
t0 a
)
1 (t t0 )
a
a
对冲激函数尺度变换说明(自学)
从 (t)定义看:
pt
1
α﹥1
pat
1
压缩1/ α
O
2
t
2
O
t
2a
2a
a
p(t)面积为1, 0时p(t) t强度为1
第三节 阶跃信号和冲激信号
函数本身有不连续点(跳变点)或其导数与积分 有不连续点的一类函数,统称为奇异信号或奇异函 数。
主要内容: •单位阶跃信号 •单位冲激信号
是两种特殊的连续信号,是实际信号或物 理现象抽象出来的理想化信号模型.
阶跃信号和冲击信号

§1.4 阶跃信号和冲激信号本节介绍函数本身有不连续点(跳变点)或其导数与积分有不连续点的一类函数统称为奇异信号或奇异函数。
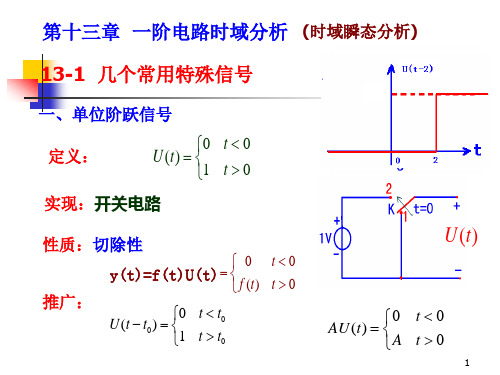
主要内容•单位斜变信号•单位阶跃信号•单位冲激信号•冲激偶信号一.单位斜变信号1.定义3.三角形脉冲由宗量t-t0=0 可知起始点为2.有延迟的单位斜变信号二.单位阶跃信号1. 定义0点无定义或1/2宗量<0 函数值为0由宗量,函数有断点,跳变点宗量>0 函数值为12. 有延迟的单位阶跃信号3.用单位阶跃信号描述其他信号其它函数只要用门函数处理(乘以门函数),就只剩下门内的部分。
符号函数:(Signum)门函数:也称窗函数三.单位冲激函数(难点)概念引出定义1定义2冲激函数的性质定义1:狄拉克(Dirac)函数函数值只在t=0时不为零;积分面积为1;t=0时,,为无界函数。
定义2则窄脉冲集中于t=0处。
★面积为1★宽度为0三个特点:★描述时移的冲激函数若面积为k,则强度为k。
三角形脉冲,双边指数脉冲,钟形脉冲,抽样函数,取τ→0极限,都可以认为是冲激函数。
冲激函数的性质1.抽样性2.奇偶性3.冲激偶4.标度变换(1) 抽样性(筛选性))()0()()(tftftδδ=对于移位情况:如果f(t)在t=0处连续,且处处有界,则有)()(tt-=δδ(2)奇偶性o t)(tsττ-τ1 (3) 冲激偶①②冲激偶的性质时移,则:③④X(4) 对 (t)的标度变换冲激偶的标度变换四.总结:R (t ),u (t ),δ(t ) 之间的关系R (t )求↓ ↑ 积(-∞<t< ∞)u (t )导↓ ↑ 分δ(t )退出')( t δ'冲激函数的性质总结(1)抽样性(2)奇偶性(3)比例性(4)微积分性质(5)冲激偶(6)卷积性质冲激函数抽样性质证明分和讨论0=t 0≠t 即,证毕。
()()()()()t f t t f t δδδ0 , 0=≠积分结果为0.flash证明奇偶性时,主要考察此函数的作用,即和其它函数共同作用的结果。
冲激信号阶跃信号关系

冲激信号阶跃信号关系嘿,朋友们!今天咱来唠唠冲激信号和阶跃信号的关系,这可有意思啦!咱先来说说冲激信号呀,这就好比是赛场上的发令枪响,“砰”的一下,瞬间爆发,时间极短但能量巨大。
它就那么一下子,却能引起很大的动静呢!而阶跃信号呢,就像是跑步比赛中运动员起跑后的加速过程,从一个状态突然跨到另一个状态,干脆利落。
你想想看,要是没有冲激信号那一下子的刺激,很多系统可能还懒洋洋地不想动呢。
它就像是个急性子的小伙伴,突然来那么一下,让一切都活跃起来了。
阶跃信号呢,则更像是个坚定的执行者,一旦决定了,就勇往直前地跨过去,绝不拖泥带水。
冲激信号和阶跃信号,它们俩呀,就像是一对好搭档。
冲激信号负责开头的震撼,阶跃信号接着把这种变化延续下去。
就好像一场精彩的演出,冲激信号是开场的绚烂烟花,阶跃信号则是随后精彩剧情的展开。
比如说在电路中吧,冲激信号可以引发瞬间的电流变化,而阶跃信号就能让电路稳定在一个新的工作状态。
这不是很神奇吗?它们相互配合,让整个系统变得丰富多彩。
再打个比方,冲激信号像是一阵突如其来的狂风,能瞬间打破平静;阶跃信号则像风过后天空的变化,从乌云密布到晴空万里,或者从晴空万里到乌云密布。
你说这冲激信号阶跃信号的关系是不是特别有意思?它们在各种领域都发挥着重要的作用呢!无论是通信、控制还是其他的科技领域,都离不开它们俩的默契配合。
所以啊,可别小瞧了这冲激信号和阶跃信号,它们虽然看起来很简单,可蕴含的力量和作用那可是大大的!它们就像隐藏在科技世界背后的小魔法师,用它们独特的魔法让一切变得有序又神奇。
总之呢,冲激信号和阶跃信号的关系真的是妙不可言,它们相互依存,相互成就,共同推动着科技的发展和进步。
咱得好好琢磨琢磨它们,才能更好地理解和运用它们呀!原创不易,请尊重原创,谢谢!。
单位阶跃信号38页PPT

若u1和u2有限值,则有 C1u1(o ) C1u1(o ) C2u2 (o ) C2u2 (o )
C1u1(o ) C2u2 (o ) C1u1(o ) C2u2 (o ) u1(o ) u2 (o ) Us
电容电压初始值:
u1(o )
C2 C1 C2
Us
u2 (o )
C1 C1 C2
(0 ) 1 C
uc (0 )
t
i
0
1
C
c ()d
0
ic ()d
0
若ic有限,则: uc (o+)= uc (o-)
或 q (o+)= q (o-)
意义:
能量不能发生突变
4
2、引例2: 图示电路
t<0 ,K打开,有 iL (0 ) 0
t=0 ,K闭合,有
iL (t)
1 L
t
uL ()d
若uL有限,则: iL (o+)=iL (o-)
1 0
1t
L
uL ()d
L
uL ()d
0
或 (o+)= (o-)
i
L
(0
)
iL
(0 ) iL (0
)
1 L
t
uL ()d
0
1
L
0 0
u
L
()d
意义:
能量不能发生突变
5
3、换路定律: (1)若ic有限,则: uc (o+)= uc (o-) 或q (o+)= q (o-) (2)若uL有限,则: iL (o+)=iL (o-) 或 (o+)= (o-)
i2 (0 ) 3A
冲激信号与阶跃信号的关系

冲激信号与阶跃信号的关系冲激信号和阶跃信号,听起来挺高大上的对吧?它们就像是信号世界里的两位好朋友,各有各的性格,却又紧密相连,常常一起出现在我们的生活中。
想象一下,冲激信号就像是一声响亮的“啪”,一下子把你从梦中惊醒;而阶跃信号呢,就像是早晨的第一缕阳光,温柔而坚定地照亮了整个房间。
这两个小家伙,一个是瞬间爆发,另一个则是稳稳地上升,形态各异,却又在信号处理中扮演着不可或缺的角色。
冲激信号,顾名思义,那个瞬间的能量释放,真的是快得让人瞠目结舌。
一眨眼,咔嚓一下,瞬间的信号就出现了,仿佛是在说:“嘿!我来了!”想想我们生活中的声音,比如鼓声,砰的一下,那可真是冲激信号的完美体现。
它就像是你小伙伴突如其来的恶作剧,瞬间打破了宁静,令人惊喜又尴尬。
冲激信号的特性是能量集中在一个极短的时间内,这种快速的变化,在信号处理中可是很有用的。
处理系统就像个敏感的侦探,能快速捕捉到这个信号的出现。
阶跃信号就像个温暖的大叔,慢慢地、稳稳地向你走来。
它不像冲激信号那么突然,而是逐步上升,就像是气温在春天一点点升高,让人感觉无比舒适。
你看,阶跃信号一出现,就开始逐渐增大,直至达到一个稳定的状态。
就像人生中的一个重要决定,开始总是有点犹豫,慢慢地才变得坚定。
信号处理中的阶跃响应,可以帮助我们理解系统对这种渐进变化的反应,简直就是一部活生生的“成长纪录片”。
冲激信号和阶跃信号之间的关系就像亲兄弟。
冲激信号可以看作是阶跃信号的“导火索”。
冲激信号一出现,阶跃信号就随之而来,就像是火花点燃了烟花,瞬间绽放,带来视觉与听觉的盛宴。
想象一下,若是在学校的操场上,老师一声令下,孩子们都像小鸟一样飞奔出去,这一瞬间就是冲激信号的感觉,而当孩子们欢笑着聚在一起,形成一片欢乐的海洋,那就是阶跃信号的表现了。
一个是瞬间的爆发,一个是持续的增长,两者相辅相成,缺一不可。
而且在实际应用中,这两者的结合更是如虎添翼。
工程师们常常利用这两种信号来测试系统的性能,看看在面对冲激信号时,系统如何快速反应,而当系统稳定下来后,又是如何应对阶跃信号的。
阶跃信号和冲激信号

t0 O
t
宗量>0 函数值为1 宗量<0 函数值为0
3.用单位阶跃信号描述其他信号
门函数:也称窗函数
ftutut
2 2
其他函数只要用门函数处理(乘以 门函数),就只剩下门内的部分。
符号函数:(Signum)
f t
1
Gτ t
O
2
t
2
sgn t
sgtn )( 11
t0 t0
O
t
st ) g u ( t ) n u ( t ) 2 ( u ( t ) 1 u(t)1[sgt)n 1(] 2
一.单位斜变信号
1. 定义
0 t0 R(t)t t0
2.有延迟的单位斜变信号
0 R (tt0) tt0
tt0 tt0
由宗量t -t0=0 可知起始点为 t 0 3.三角形脉冲
f(t) K R(t)
0
0t
其它
R(t) 1
O1
t
R(t t0 ) 1
O t0 t0 1 t
f (t) K
O
t
二.单位阶跃信号
四.总结: R(t),u(t), (t) 之间的关系R(t )来自u(t )1 1
t
O1
O
R(t) 求 ↓↑积
u(t) 导 ↓↑分
(t)
(t)
(1)
t
t
O
(-<t< )
冲激函数的性质总结
(1)抽样性
f(t)(t) f(0 )(t)
(5)冲激偶
( t) (t)
f (t)(t)dtf(0)
(t)dt0
(2)奇偶性
(t)(t)
t (t)dt(t)
信号和系统常用信号介绍

x(t)dt 2
Ae
(
t
)
2
dt
2A
A
0
2
二、离散时间信号:
1、单位样值序列: (n)
函数式:
(n)
1 0
n0 n0
波形图:
(n)
1
0
n
位移:
1 (n n0 ) 0
n n0 n n0
(n n0)
1
0 n0
n
• 抽样性:
设有序列x(n) ,则有
x(n)
1 2 0
12 3 4 5
n
x(t)
1
x(t)
1
x(t)
(1)
0
x(t)
x(t)
1
1
t
2
2
t
0
t
x(t)
1
x(t)
1
t
22
t
0
t
单位冲激信号在信号与系统的理 论中,是一个重要的基本信号,与 t 运动学中的质点、电学中的点电荷 一样,是一个理ቤተ መጻሕፍቲ ባይዱ的模型。
•单位冲激信号的性质: ⑴ 抽样性(筛选性):
设x(t)在t=0与t0处连续,
• 欧拉公式:
cos t 1 (e jt e jt ) 2
e jt cos t j sin t
sin t 1 (e jt e jt ) 2j
e jt cos t j sin t
正余弦信号是我们熟悉的常用基本信号,它有很好的特 性,与指数信号类似,它们的导数和积分依然是正余弦信 号,在正弦交流电路分析中我们知道,角频率为Ω的正弦 信号作用于电路,其输出还是角频率为Ω的正弦信号。
称为它们的初相位,Ω是它们的角频率。
单位阶跃信号
iL (o-)= 5A
13-3 电荷守恒与磁链守恒
一、电荷守恒定律 引例:图示电路 a
+ u1
- + u2 -
t<0 ,K打开,电路稳定,有 u 1 (0 ) 0 u 2 ( 0 ) 0 t=0 ,K闭合,在节点a有
u1 du u du2 C1 1 2 C2 R1 dt R2 dt
u c (0 ) u c (0 ) 18V
t o 等效电路 :
i1 (o ) 0, i 2 (o ) 3A
ic
i c (o ) 1A
u L 2 (o ) 9V u L1 (o ) 15V
u L1 u L2
14
电路初始值确定
电路初始值
t=0,K闭,有
u c (0 ) u c (0 ) 18V
L1 、 L2 和 is =3A组成割集,由磁链守恒定律,有
L1i1 (o ) L 2i 2 (o ) L1i1 (o ) L 2i 2 (o ) 又 i1 (o ) i 2 (o ) 3 0 i1 (o ) 0, i 2 (o ) 3A
i L (0 ) i L (0 ) 1A
o+等效电路:
ic (o+)
i c (o ) i L (o ) 1A
u R (o ) 8V
+
uR -
u L (o ) 0 i 2 (o ) Байду номын сангаас 0
u 2 (o ) 0
16
练习: 图示电路,t<0,K在1,电路稳定,t=0,K从1到2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.5 冲激信号和阶跃信号的傅里叶变换
2.5.1 冲激信号
由傅里叶变换定义及冲激信号的抽样特性很容易求得(t)函数的FT为
冲激函数的频谱等于常数,也就是说,在整个频率范围内频谱都是均匀的。
在时域中波形变化剧烈的冲激函数包含幅度相等的所有频率分量,这种频谱常称作"均匀谱"或"白色谱"。
2.5.2 直流信号
如前所述,冲激信号的频谱是常数,那么时域为常数的信号(直流信号)的频谱是否为冲激函数呢?
我们来考虑()的傅里叶逆变换,即
这也就是说
上式意味着
式中的E为常数。
这表明,直流信号的频谱是位于w=0的冲激函数,这与直流信号的物理概念是一致的。
2.5.3单位阶跃信号
单位阶跃函数同样不满足绝对可积条件,但仍存在傅里叶变换。
前面我们已经讲述了符号函数的傅里叶变换,下面我们借助符号函数来求阶跃信号的FT。
单位阶跃函数U(t)可用符号函数来表示,即
再利用直流信号与符号函数的傅里叶变换
可得单位阶跃函数的傅里叶变换为
单位阶跃函数及其频谱如下图所示。
由图可知,U(t)在t>0时等同于直流信号,但它又不是纯粹的直流信号,它在t=0处有跳变,因此其频谱不是仅在=0处有一个冲激函数(这对应于信号的直流特性),而且还会含有其它众多的频率分量。
为什么会有众多的频率分量呢?这是因为信号在时域零点处有跳变!由于时域的剧烈变化,相应的频域中的分量将是无限的。
还记得我们在前面讲周期矩形脉冲信号所提及的"时域跳变将使频域包含无限的频率分量"的结论吗?这儿就是一个很好的例证。
大家可以翻回去看看,是不是这样。
图2-11 (a) 单位阶跃函数的波形 (b) 信号的幅度谱。
