计量经济学第三版-潘省初-第4章
计量经济学第四章完整课件

130.8
X:人均消费
X1:人均食 品消费
GP:居民消 费价格指数
FP:居民食品 消费价格指数
XC:人均消 费(90年价)
Q:人均食品 消费(90年价)
P0:居民消费 价格缩减指数 (1990=100)
P:居民食品 消费价格缩减 指数 (1990=100
中
1800
国
1600
城
Q
镇
1400
居
1200
1986 799.0 418.9
107.0
107.2
826.6
437.8
96.7
95.7
1987 884.4 472.9
108.8
112.0
899.4
490.3
98.3
96.5
1988 1104.0 567.0
120.7
125.2
1085.5
613.8
101.7
92.4
1989 1211.0 660.0
第四章 非线性回归模型的形式
一、模型的类型与变换 二、非线性回归实例
在实际经济活动中,经济变量的关系是复杂 的,直接表现为线性关系的情况并不多见。
如著名的恩格尔曲线(Engle curves)表现为幂 函数曲线形式、宏观经济学中的菲利普斯曲线 (Pillips cuves)表现为双曲线形式等。
但是,大部分非线性关系又可以通过一些简 单的数学处理,使之化为数学上的线性关系,从 而可以运用线性回归的方法进行计量经济学方面 的处理。
116.3
114.4
1262.5
702.2
95.9
94.0
1990 1278.9 693.8
101.3
计量经济学 第四章

100%
统计检验
利用统计量对模型参数进行假设 检验,判断参数是否显著。
80%
计量经济学检验
包括模型的异方差性、自相关性 、多重共线性等问题的检验。
模型的修正方法
增加解释变量
如果模型存在遗漏变量,可以通过增加解释变量来 修正模型。
删除解释变量
如果模型中某些解释变量不显著或存在多重共线性 ,可以考虑删除这些变量。
模型表达式
Y = β0 + β1X + ε
最小二乘法
通过最小化残差平方和来估计参数β0和β1
参数解释
β0为截距项,β1为斜率项,ε为随机误差项
模型的检验
包括拟合优度检验、显著性检验等
多元线性回归模型
01
02
03
04
模型表达式
参数解释
最小二乘法
Y = β0 + β1X1 + β2X2 + ... + βkXk + ε
最小二乘法估计量的性质
线性性
最小二乘法估计量是随机样本的线性组合。
无偏性
最小二乘法估计量的期望值等于总体参数的 真实值。
有效性
在所有无偏估计量中,最小二乘法估计量的 方差最小。
一致性
随着样本量的增加,最小二乘法估计量收敛 于总体参数的真实值。
最小二乘法的计算步骤
构造设计矩阵X和响应向量Y。 计算设计矩阵X的转置矩阵X'。 计算X'X和X'Y。
求解线性方程组X'Xβ=X'Y,得到回归系 数的最小二乘估计β^=(X'X)^(-1)X'Y。
根据β^计算因变量的拟合值Y^=Xβ^。
计算残差e=Y-Y^,以及残差平方和 RSS=e'e。
计量经济学第四章非线性回归模型的线性化

第四章 非线性回归模型的线性化以上介绍了线性回归模型。
但有时候变量之间的关系是非线性的。
例如 y t = α 0 + α11βt x + u t y t = α 0 t x e 1α+ u t上述非线性回归模型是无法用最小二乘法估计参数的。
可采用非线性方法进行估计。
估计过程非常复杂和困难,在20世纪40年代之前几乎不可能实现。
计算机的出现大大方便了非线性回归模型的估计。
专用软件使这种计算变得非常容易。
但本章不是介绍这类模型的估计。
另外还有一类非线性回归模型。
其形式是非线性的,但可以通过适当的变换,转化为线性模型,然后利用线性回归模型的估计与检验方法进行处理。
称此类模型为可线性化的非线性模型。
下面介绍几种典型的可以线性化的非线性模型。
4.1 可线性化的模型⑴ 指数函数模型y t = t t ubx ae + (4.1)b >0 和b <0两种情形的图形分别见图4.1和4.2。
显然x t 和y t 的关系是非线性的。
对上式等号两侧同取自然对数,得Lny t = Lna + b x t + u t (4.2)令Lny t = y t *, Lna = a *, 则y t * = a * + bx t + u t (4.3) 变量y t * 和x t 已变换成为线性关系。
其中u t 表示随机误差项。
010203040501234XY 1图4.1 y t =tt u bx ae+, (b > 0) 图4.2 y t =tt u bx ae+, (b < 0)⑵ 对数函数模型y t = a + b Ln x t + u t (4.4)b >0和b <0两种情形的图形分别见图4.3和4.4。
x t 和y t 的关系是非线性的。
令x t * = Lnx t , 则y t = a + b x t * + u t (4.5)变量y t 和x t * 已变换成为线性关系。
图4.3 y t = a + b Lnx t + u t , (b > 0) 图4.4 y t = a + b Lnx t + u t , (b < 0)⑶ 幂函数模型y t = a x t b t u e (4.6)b 取不同值的图形分别见图4.5和4.6。
计量经济学第三版习题答案

计量经济学第三版习题答案计量经济学是一门研究经济现象的定量方法的学科。
它通过建立数学模型和运用统计方法来分析经济数据,从而揭示经济现象的规律和关系。
在学习计量经济学的过程中,习题是非常重要的一部分,通过解答习题可以加深对理论知识的理解和应用能力的培养。
本文将为读者提供《计量经济学第三版》习题的答案,帮助读者更好地掌握这门学科。
第一章:计量经济学导论1. 计量经济学的定义是什么?答:计量经济学是一门运用数学和统计方法对经济现象进行定量分析的学科。
2. 为什么计量经济学在经济学研究中具有重要地位?答:计量经济学通过建立数学模型和运用统计方法,能够对经济现象进行定量分析,揭示经济规律和关系,为经济学研究提供了重要的工具和方法。
3. 计量经济学的基本步骤是什么?答:计量经济学的基本步骤包括:问题的提出、理论模型的建立、数据的收集、模型的估计和检验、结果的解释和政策的制定。
第二章:线性回归模型的假设与估计1. 线性回归模型的基本形式是什么?答:线性回归模型的基本形式是Y = β0 + β1X1 + β2X2 + … + βkXk + ε,其中Y 是因变量,X1、X2、…、Xk是自变量,β0、β1、β2、…、βk是参数,ε是误差项。
2. 线性回归模型的假设有哪些?答:线性回归模型的假设包括:线性关系假设、零条件均值假设、同方差性假设、独立性假设。
3. 如何对线性回归模型进行参数估计?答:线性回归模型的参数估计可以通过最小二乘法进行。
最小二乘法的基本思想是使观测值与模型预测值的误差平方和最小化,从而得到参数的估计值。
第三章:线性回归模型的假设检验与模型选择1. 线性回归模型的显著性检验是什么?答:线性回归模型的显著性检验是通过检验回归系数的估计值是否显著不等于零来判断自变量对因变量的影响是否显著。
2. 如何进行线性回归模型的显著性检验?答:线性回归模型的显著性检验可以通过计算t统计量或F统计量进行。
t统计量用于检验单个回归系数的显著性,F统计量用于检验整体回归模型的显著性。
【《计量经济学》(第三版)课件】计量三4

YY BXY YXB BXXB
20
• 当 V对 b0 ,b1, bK的一阶偏导数都等于0
V
b0
BV 2XY 2XXB 0
V
bK
XXB XY
B XX1 XY
21
三、最大似然估计
多元线性回归模型满足经典假设: Y=Xβ+ε
模型的似然函数为: L=p(Y)=p(ε)=1/(2πσ2)n/2.exp(-1/2σ2(Y-Xβ)’ (Y-Xβ))
V ar Xβ BVar
X 2 XX1 X*' 2 1 X XX X 1 *' 2
t
Y * Yˆ*
~ t(n K 1)
S 2 (1 X* (X'X)1 X*')
17
• 置信度为 1 的区间预测 Yˆ* t /2 S 1 X*(X'X)1 X*' Y * Yˆ* t /2 S 1 X*(X'X)1 X*'
18
附录4-1 多元线性回归分析的矩阵表示
Y1
Y
Yn
Y1 0 1 X 11 K X K1 1 Yn 0 1 X1n K X K n
X i1
X i
X i n
1
0
l
1
K
1
n
1 X11
X l, X1, , X K
1 X1n
且解释变量之间不存在线性关系
• 服从正态分布
i
5
第二节 多元线性回归参数估计
一、最小二乘估计 二、最小二乘估计的向量、矩阵形式 三、最大似然估计 四、投资函数模型参数估计
6
一、最小二乘估计
样本回归方程
潘省初计量经济学参考答案

(")原假设 -&:!!*#& 备择假设 -*:!!*#& 检验统计量#!(!!.*#&)//0(!!)!(&#’(.*#&)/&#)(($!.&#,’+ 查#表,#&!#&#&)((+)!)#"&$ ,因为"#"! &#,’+#)#"&$ ,故接受原假设:
!!*#&。
,’ 对于 $&!)(& ,点预测值 "!&!*&%&#,&1)(&!)"(#& "!&的,(2置信区间为:
(!)斜率系数为负符合经济理论和常识,因为如果美国价格上升快于德国, 则美国消费者将倾向于买德国货,这就增大了对马克的需求,导致马克的升值。
(,)在这种情况下,斜率系数被预期为正数,因为,德国 234相对于美国 234 越高,德国相对的通货膨胀就越高,这将导致美元对马克升值。
5)(#) .$/+01(6)5(+!(7#+,#8#55+(56#’(+*. .$/+01(6)5(+!(7#+,#8#(*+.-6#,.+-( .$/+01(6)5(+!(7#+,#8#-5+-!6#(.+5-
& % "!&(#&#&)((*))))*!" *+*/,+($&)$$))/ -)
.)"(()#))+*&#** &*+*/*)+()(&))&&))/3&&&.)"((&#),
潘省初计量经济学中级教程习题参考答案

潘省初计量经济学中级教程习题参考答案计量经济学中级教程习题参考答案第一章绪论1.1 一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说)(2)建立计量经济模型(3)收集数据(4)估计参数(5)假设检验(6)预测和政策分析1.2 我们在计量经济模型中列出了影响因变量的解释变量,但它(它们)仅是影响因变量的主要因素,还有很多对因变量有影响的因素,它们相对而言不那么重要,因而未被包括在模型中。
为了使模型更现实,我们有必要在模型中引进扰动项u来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3 时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4 估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y 就是一个估计量,1n ii Y Y n ==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 经典线性回归模型2.1 判断题(说明对错;如果错误,则予以更正)(1)对(2)对(3)错只要线性回归模型满足假设条件(1)~(4),OLS 估计量就是BLUE 。
(4)错R 2 =ESS/TSS 。
(5)错。
我们可以说的是,手头的数据不允许我们拒绝原假设。
(6)错。
因为∑=22)ˆ(t x Var σβ,只有当∑2t x 保持恒定时,上述说法才正确。
2.2 应采用(1),因为由(2)和(3)的回归结果可知,除X 1外,其余解释变量的系数均不显著。
庞皓计量经济学第三版课后习题及答案 顶配
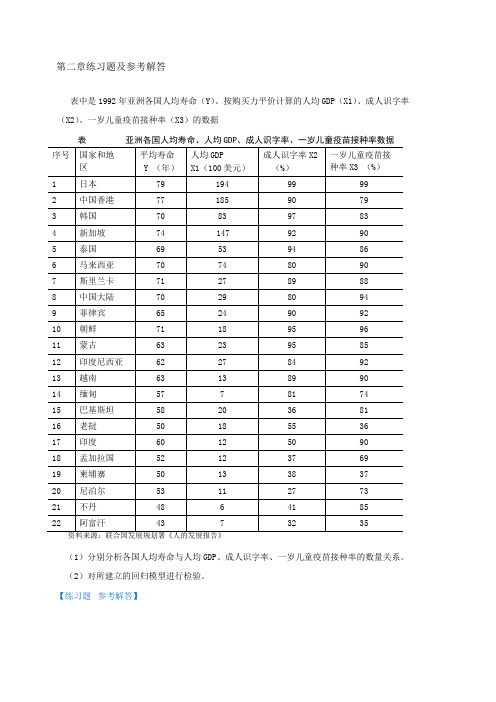
第二章练习题及参考解答表中是1992年亚洲各国人均寿命(Y)、按购买力平价计算的人均GDP(X1)、成人识字率(X2)、一岁儿童疫苗接种率(X3)的数据表亚洲各国人均寿命、人均GDP、成人识字率、一岁儿童疫苗接种率数据(1)分别分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系。
(2)对所建立的回归模型进行检验。
【练习题参考解答】(1)分别设定简单线性回归模型,分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系:1)人均寿命与人均GDP 关系Y i 1 2 X1i u i估计检验结果:2)人均寿命与成人识字率关系3)人均寿命与一岁儿童疫苗接种率关系(2)对所建立的多个回归模型进行检验由人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命回归结果的参数t 检验值均明确大于其临界值,而且从对应的P 值看,均小于,所以人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命都有显着影响.(3)分析对比各个简单线性回归模型人均寿命与人均GDP 回归的可决系数为人均寿命与成人识字率回归的可决系数为人均寿命与一岁儿童疫苗接种率的可决系数为相对说来,人均寿命由成人识字率作出解释的比重更大一些为了研究浙江省财政预算收入与全省生产总值的关系,由浙江省统计年鉴得到以下数据:表浙江省财政预算收入与全省生产总值数据的显着性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2011 年,全省生产总值为32000 亿元,比上年增长%,利用计量经济模型对浙江省2011 年的财政预算收入做出点预测和区间预测(3)建立浙江省财政预算收入对数与全省生产总值对数的计量经济模型,. 估计模型的参数,检验模型的显着性,并解释所估计参数的经济意义【练习题参考解答】建议学生独立完成由12对观测值估计得消费函数为:(1)消费支出C的点预测值;(2)在95%的置信概率下消费支出C平均值的预测区间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R2 0.99
(9.6) (0.003) (0.114)
Y和X的计量单位为10亿美元 (按1972不变价格计算).
P
食品价格平减指数 总消费支出价格平减指数
100,(1972
100)
3
多元线性回归模型中斜率系数的含义
上例中斜率系数的含义说明如下: 价格不变的情况下,个人可支配收入每上升10
亿美元(1个billion),食品消费支出增加1.12亿 元(0.112个 billion)。
X 1n
β2 X 2n
β3 X 3n
... βK
X Kn
un
6
其矩阵形式为: Y X u
其中
Y1
Y
Y2
... Yn
1
X
1
...
1
X11 X12 ... X1n
... ... ... ...
X K1
X
K
2
...
X
Kn
0
1
2
,
...
K
u1
u
u2 ... un
t=1,2, … n
8
除上面4条外,在多个解释变量的情况下,还有 两个条件需要满足: (5)(K+1)< n;
即观测值的数目要大于待估计的参数的个数 (要有足够数量的数据来拟合回归线)。 (6)各解释变量之间不存在严格的线性关系。
上述假设条件可用矩阵表示为以下四个条件:
9
A1. E(u)=0
A2. E(uu) 2In
11
二.最小二乘估计
我们的模型是:
Yt 0 1X1t 2 X 2t ... k X kt ut
t=1,2,…n
问题是选择 ˆ0 , ˆ1,...., ˆk ,使得残差平方和最小。
残差为:
et Yt Yˆt
Yt ˆ0 ˆ1 X1t .... ˆK X Kt
12
要使残差平方和
S et2 Yt ˆ0 ˆ1X1t ... ˆK X Kt 2
为最小,则应有:
S
ˆ 0
0,
S
ˆ1
0,
...,
S
ˆ K
0
我们得到如下K+1个方程(即正规方程):
13
β0 n
β1 X1t ...... β K X Kt Yt
β 0 X 1t β1 X 1t 2 ...... β K X 1t X Kt X 1tYt
β 0 X 2t β1 X 2t X 1t ...... β K X 2t X Kt X 2tYt. Nhomakorabea....
......
......
......
β 0 X kt β1
X kt X 1t ...... β K
X Kt 2
X ktYt
按矩阵形式,上述方程组可表示为:
第四章 多元线性回归模型
1
第一节 多元线性回归模型的概念
在许多实际问题中,我们所研究的因变量的变动 可能不仅与一个解释变量有关。因此,有必要考虑线 性模型的更一般形式,即多元线性回归模型:
Yt
β 0
β1 X1t
β 2
X
2t
... βk X kt
ut
t=1,2,…,n
在这个模型中,Y由X1、X2、X3、… XK所解释, 有K+1个未知参数β0、β1、β2、…βK 。
收入变动对消费额的总影响=直接影响+间接影响。 (间接影响:收入影响流动资产拥有量影响消费额)
但在模型中这种间接影响应归因于流动资产,而不是收入 ,因而,β2只包括收入的直接影响。
在下面的模型中: Ct Dt ut , t 1,2,..., n
这里,β是可支配收入对消费额的总影响,显然β和β2的
14
n
X1t
...
X Kt
X1t X1t 2
...
X Kt X1t
... ... ... ...
X Kt
X1t X Kt
...
X Kt 2
β 0
β1
...
=
由于
u1
uu
u2 ... un
u1
u2
...
un
u12 u2u1
u1u2 u22
...... ......
u1un
u2un
.................................
unu1 unu2 ...... un2
显然, E(uu) 2In 仅当
E(ui uj)=0 , i≠j E(ut2) = σ2, t=1,2,…,n 这两个条件成立时才成立,因此, 此条件相当前面条件
这里,“斜率”βj的含义是其它变量不变的情况 下,Xj改变一个单位对因变量所产生的影响。
2
例1:
Y
β0
β 1
X
β2P u
其中,Y=在食品上的总支出 X=个人可支配收入 P=食品价格指数
用美国1959-1983年的数据,得到如下回归结果(括号中数 字为标准误差):
Yˆ 116.7 0.112X 0.739P
(2), (3)两条,即各期扰动项互不相关,并具有常数方差。10
A3. X 是一个非随机元素矩阵。 A4. Rank(X) = (K+1) < n. ------相当于前面 (5)
、 (6) 两 条 即矩阵X的秩 =(K+1)< n 当然,为了后面区间估计和假设检验的需要,还 要加上一条:
A5. u~t N(0, 2 ) ,t=1,2,…n
含义是不同的。
5
回到一般模型
Yt
β 0
β1 X1t
β2 X 2t
... βk X kt
ut
t=1,2,… ,n
即对于n组观测值,有
Y1
β0
β 1
X
11
β2
X
21
β3
X
31
... βK
X
K1
u1
Y2
β0
β 1
X12
β2 X 22
β3 X 32
... βK
XK2
u2
......
Yn
β0
β 1
7
第二节 多元线性回归模型的估计
多元线性回归模型的估计与双变量线性模型类似,仍采用 OLS法。当然,计算要复杂得多,通常要借助计算机。理论 推导需借助矩阵代数。下面给出普通最小二乘法应用于多元 线性回归模型的假设条件、估计结果及所得到的估计量的性 质。
一.假设条件 (1)E(ut)=0, t=1,2,…,n (2)E(ui uj)=0, i≠j (3)E(ut2)=σ2, t=1,2,…,n (4)Xjt是非随机量, j=1,2, … k
收入不变的情况下,价格指数每上升一个点, 食品消费支出减少7.39亿元(0.739个billion)
4
例2:
Ct
β 1
β 2 Dt
β3Lt
ut
其中,Ct=消费,Dt=居民可支配收入 Lt=居民拥有的流动资产水平
β2的含义是,在流动资产不变的情况下,可支配收入变动 一个单位对消费额的影响。这是收入对消费额的直接影响。
