计量经济学第三版-潘省初-第10章 定性选择问题
计量经济学(伍德里奇第三版中文版)课后习题答案

第1章解决问题的办法1.1(一)理想的情况下,我们可以随机分配学生到不同尺寸的类。
也就是说,每个学生被分配一个不同的类的大小,而不考虑任何学生的特点,能力和家庭背景。
对于原因,我们将看到在第2章中,我们想的巨大变化,班级规模(主题,当然,伦理方面的考虑和资源约束)。
(二)呈负相关关系意味着,较大的一类大小是与较低的性能。
因为班级规模较大的性能实际上伤害,我们可能会发现呈负相关。
然而,随着观测数据,还有其他的原因,我们可能会发现负相关关系。
例如,来自较富裕家庭的儿童可能更有可能参加班级规模较小的学校,和富裕的孩子一般在标准化考试中成绩更好。
另一种可能性是,在学校,校长可能分配更好的学生,以小班授课。
或者,有些家长可能会坚持他们的孩子都在较小的类,这些家长往往是更多地参与子女的教育。
(三)鉴于潜在的混杂因素- 其中一些是第(ii)上市- 寻找负相关关系不会是有力的证据,缩小班级规模,实际上带来更好的性能。
在某种方式的混杂因素的控制是必要的,这是多元回归分析的主题。
1.2(一)这里是构成问题的一种方法:如果两家公司,说A和B,相同的在各方面比B公司à用品工作培训之一小时每名工人,坚定除外,多少会坚定的输出从B公司的不同?(二)公司很可能取决于工人的特点选择在职培训。
一些观察到的特点是多年的教育,多年的劳动力,在一个特定的工作经验。
企业甚至可能歧视根据年龄,性别或种族。
也许企业选择提供培训,工人或多或少能力,其中,“能力”可能是难以量化,但其中一个经理的相对能力不同的员工有一些想法。
此外,不同种类的工人可能被吸引到企业,提供更多的就业培训,平均,这可能不是很明显,向雇主。
(iii)该金额的资金和技术工人也将影响输出。
所以,两家公司具有完全相同的各类员工一般都会有不同的输出,如果他们使用不同数额的资金或技术。
管理者的素质也有效果。
(iv)无,除非训练量是随机分配。
许多因素上市部分(二)及(iii)可有助于寻找输出和培训的正相关关系,即使不在职培训提高工人的生产力。
庞皓计量经济学第三版课后习题及答案 顶配
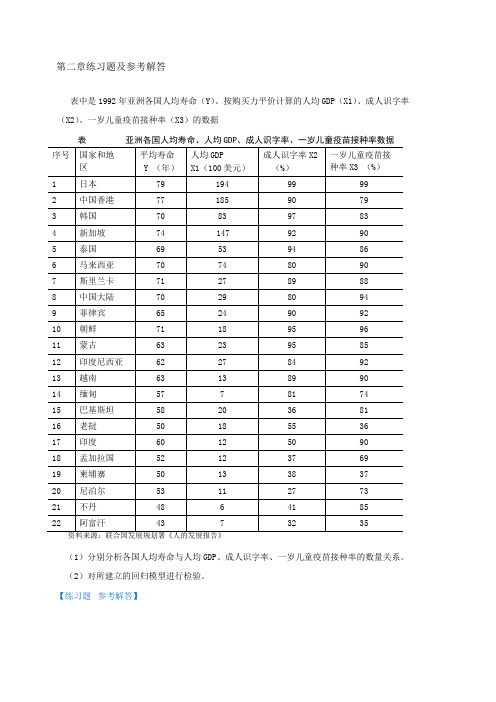
第二章练习题及参考解答表中是1992年亚洲各国人均寿命(Y)、按购买力平价计算的人均GDP(X1)、成人识字率(X2)、一岁儿童疫苗接种率(X3)的数据表亚洲各国人均寿命、人均GDP、成人识字率、一岁儿童疫苗接种率数据(1)分别分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系。
(2)对所建立的回归模型进行检验。
【练习题参考解答】(1)分别设定简单线性回归模型,分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系:1)人均寿命与人均GDP 关系Y i 1 2 X1i u i估计检验结果:2)人均寿命与成人识字率关系3)人均寿命与一岁儿童疫苗接种率关系(2)对所建立的多个回归模型进行检验由人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命回归结果的参数t 检验值均明确大于其临界值,而且从对应的P 值看,均小于,所以人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命都有显着影响.(3)分析对比各个简单线性回归模型人均寿命与人均GDP 回归的可决系数为人均寿命与成人识字率回归的可决系数为人均寿命与一岁儿童疫苗接种率的可决系数为相对说来,人均寿命由成人识字率作出解释的比重更大一些为了研究浙江省财政预算收入与全省生产总值的关系,由浙江省统计年鉴得到以下数据:表浙江省财政预算收入与全省生产总值数据的显着性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2011 年,全省生产总值为32000 亿元,比上年增长%,利用计量经济模型对浙江省2011 年的财政预算收入做出点预测和区间预测(3)建立浙江省财政预算收入对数与全省生产总值对数的计量经济模型,. 估计模型的参数,检验模型的显着性,并解释所估计参数的经济意义【练习题参考解答】建议学生独立完成由12对观测值估计得消费函数为:(1)消费支出C的点预测值;(2)在95%的置信概率下消费支出C平均值的预测区间。
计量经济学第三版庞浩)版课后答案全
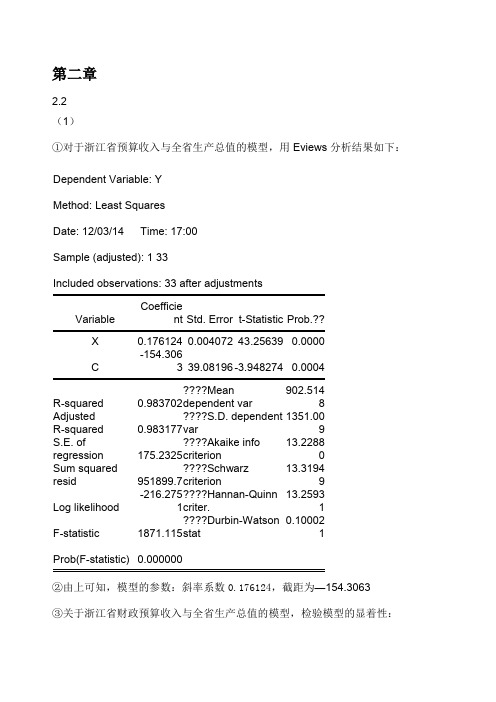
第二章2.2 (1)①对于浙江省预算收入与全省生产总值的模型,用Eviews 分析结果如下: Dependent Variable: Y Method: Least Squares Date: 12/03/14 Time: 17:00 Sample (adjusted): 1 33Included observations: 33 after adjustmentsVariableCoefficient Std. Error t-Statistic Prob.?? X 0.176124 0.004072 43.25639 0.0000 C-154.3063 39.08196 -3.948274 0.0004 R-squared 0.983702 ????Mean dependent var 902.5148Adjusted R-squared 0.983177 ????S.D. dependent var 1351.009S.E. of regression 175.2325 ????Akaike info criterion 13.2288Sum squared resid 951899.7 ????Schwarz criterion 13.31949 Log likelihood -216.2751 ????Hannan-Quinn criter. 13.25931 F-statistic1871.115 ????Durbin-Watson stat 0.100021Prob(F-statistic) 0.000000②由上可知,模型的参数:斜率系数0.176124,截距为—154.3063 ③关于浙江省财政预算收入与全省生产总值的模型,检验模型的显着性:1)可决系数为0.983702,说明所建模型整体上对样本数据拟合较好。
2)对于回归系数的t检验:t(β2)=43.25639>t0.025(31)=2.0395,对斜率系数的显着性检验表明,全省生产总值对财政预算总收入有显着影响。
计量经济学实验答案--第三版

实验一P42第二章第6题=+GDP+Dependent Variable: YMethod: Least SquaresDate: 01/11/08 Time: 09:03Sample: 1985 1998Included observations: 14Variable Coefficient Std.Errort-Statistic Prob.C12596.271244.56710.121010.0000GDP26.954154.1203006.5417920.0000 R-squared0.781002 Meandependent var20168.57Adjusted R-squared 0.762752 S.D. dependentvar3512.487S.E. of regression 1710.865 Akaike infocriterion17.85895Sum squared resid 35124719 Schwarzcriterion17.95024Log likelihood-123.0126 F-statistic42.79505Durbin-Watsonstat0.859998 Prob(F-statistic)0.000028(10.1) ( 6.5), =0.78 =0.76(一)对回归方程的结构分析:是这个样本回归方程的斜率,它表示GDP每增加1亿元,某市将增加26.95的货物运输量;是样本回归方程的截距,它表示不受GDP影响的某市的货物运输量。
(二)统计检验=0.78,说明总离差平方和的78%被样本回归直线解释,有22%未被解释,因此,样本回归直线的拟合优度是可以的。
给出显著水平,查自由度v=14-2=12的t分布表,得临界值,,,固回归系数均显著不为零,回归模型中应包含常数项,GDP对Y有显著影响。
(三)预测2000年的某市货物运输量假如2000年某市以1980年不变价的国内生产总值为620亿元,得到2000年货物运输量的预测值29307.84万吨。
(完整word版)计量经济学中级教程(潘省初 清华大学出版社)课后习题答案

计量经济学中级教程习题参考答案第一章 绪论1.1 一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据(4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 我们在计量经济模型中列出了影响因变量的解释变量,但它(它们)仅是影响因变量的主要因素,还有很多对因变量有影响的因素,它们相对而言不那么重要,因而未被包括在模型中。
为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3 时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4 估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y 就是一个估计量,1nii YYn==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 经典线性回归模型2.1 判断题(说明对错;如果错误,则予以更正) (1)对 (2)对 (3)错只要线性回归模型满足假设条件(1)~(4),OLS 估计量就是BLUE 。
(4)错R 2 =ESS/TSS 。
(5)错。
我们可以说的是,手头的数据不允许我们拒绝原假设。
(6)错。
因为∑=22)ˆ(tx Var σβ,只有当∑2t x 保持恒定时,上述说法才正确。
2.2 应采用(1),因为由(2)和(3)的回归结果可知,除X 1外,其余解释变量的系数均不显著。
计量经济学第三版习题答案

计量经济学第三版习题答案计量经济学是一门研究经济现象的定量方法的学科。
它通过建立数学模型和运用统计方法来分析经济数据,从而揭示经济现象的规律和关系。
在学习计量经济学的过程中,习题是非常重要的一部分,通过解答习题可以加深对理论知识的理解和应用能力的培养。
本文将为读者提供《计量经济学第三版》习题的答案,帮助读者更好地掌握这门学科。
第一章:计量经济学导论1. 计量经济学的定义是什么?答:计量经济学是一门运用数学和统计方法对经济现象进行定量分析的学科。
2. 为什么计量经济学在经济学研究中具有重要地位?答:计量经济学通过建立数学模型和运用统计方法,能够对经济现象进行定量分析,揭示经济规律和关系,为经济学研究提供了重要的工具和方法。
3. 计量经济学的基本步骤是什么?答:计量经济学的基本步骤包括:问题的提出、理论模型的建立、数据的收集、模型的估计和检验、结果的解释和政策的制定。
第二章:线性回归模型的假设与估计1. 线性回归模型的基本形式是什么?答:线性回归模型的基本形式是Y = β0 + β1X1 + β2X2 + … + βkXk + ε,其中Y 是因变量,X1、X2、…、Xk是自变量,β0、β1、β2、…、βk是参数,ε是误差项。
2. 线性回归模型的假设有哪些?答:线性回归模型的假设包括:线性关系假设、零条件均值假设、同方差性假设、独立性假设。
3. 如何对线性回归模型进行参数估计?答:线性回归模型的参数估计可以通过最小二乘法进行。
最小二乘法的基本思想是使观测值与模型预测值的误差平方和最小化,从而得到参数的估计值。
第三章:线性回归模型的假设检验与模型选择1. 线性回归模型的显著性检验是什么?答:线性回归模型的显著性检验是通过检验回归系数的估计值是否显著不等于零来判断自变量对因变量的影响是否显著。
2. 如何进行线性回归模型的显著性检验?答:线性回归模型的显著性检验可以通过计算t统计量或F统计量进行。
t统计量用于检验单个回归系数的显著性,F统计量用于检验整体回归模型的显著性。
计量经济学第十章练习题及参考答案

第十章练习题及参考解答10.1表10.10是某国的宏观经济季度数据。
其中, GDP为国内生产总值,PDI为个人可支配收入,PCE为个人消费支出,利润为公司税后利润,红利为公司净红利支出。
表10.10 1980~2001年某国宏观经济季度数据(单位: 亿元)1) 画出利润和红利的散点图,并直观地考察这两个时间序列是否是平稳的。
2) 应用单位根检验分别检验利润和红利两个时间序列是否是平稳的。
3) 分别检验GDP 、PDI 和PCE 等序列是否平稳,并判定其单整阶数是否相同?练习题10.1参考解答:1) 利润和红利的散点图如下,从图中可看出,利润和红利序列均值和方差不稳定,因此可能是非平稳的。
2)利润序列有截距项,在Eviews5.0中选取截距项,同时最大滞后长度取11进行单位根检验,检验结果如下,Null Hypothesis: PFT has a unit root Exogenous: Constant, Linear TrendLag Length: 0 (Automatic based on SIC, MAX LAG=11)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -1.797079 0.6978Test critical values:1% level -4.066981 5% level -3.46229210% level-3.157475t 统计量大于所有显著性水平下的MacKinnon 临界值,故不能拒绝原假设,该序列是不平稳的。
红利序列有截距项和趋势项,在Eviews5.0中选取截距项和趋势项,同时最大滞后长度取11进行单位根检验,检验结果如下,Null Hypothesis: BNU has a unit rootExogenous: Constant, Linear TrendLag Length: 1 (Automatic based on SIC, MAX LAG=11)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -2.893559 0.1698Test critical values: 1% level -4.0682905% level -3.46291210% level -3.157836*MacKinnon (1996) one-sided p-values.t统计量大于所有显著性水平下的MacKinnon临界值,故不能拒绝原假设,该序列是不平稳的。
潘省初计量经济学第3版

β 0 X 2t β1 X 2t X 1t ...... β K X 2t X Kt X 2tYt
......
......
......
......
β 0 X kt β1
X kt X 1t ...... β K
X Kt 2
X ktYt
按矩阵形式,上述方程组可表示为:
X'
1 Y1
X 1n
Y2
... ...
X
Kn
Yn
Y
即 ( X ' X )β X 'Y
β ( X X )1 X Y
14
三. 最小二乘估计量 β的性质 我们的模型为 Y X u
估计式为
Yˆ
Xβ
1.β 的均值
β ( X X )1 X Y
( X X )1 X ( Xβ u)
( X X )1 X Xβ ( X X )1 X u
收入不变的情况下,价格指数每上升一个点, 食品消费支出减少7.39亿元(0.739个billion)
3
例2:
Ct
β 1
β 2 Dt
β 3 Lt
ut
其中,Ct=消费,Dt=居民可支配收入 Lt=居民拥有的流动资产水平
β2的含义是,在流动资产不变的情况下,可支配收入变动 一个单位对消费额的影响。这是收入对消费额的直接影响。
为求Var( β ),我们考虑
E
β
β
β
β
β0 β0
E
β1 β1
...
β
0
β
0
β1 β1
...
βK
βK
β
K
βK
17
Var(β 0 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
我们在第四章中曾介绍解释变量为虚拟变量的模 本章要讨论的是因变量为虚拟变量的情形。 型,本章要讨论的是因变量为虚拟变量的情形。 在这种模型中,因变量描述的是特征、 在这种模型中,因变量描述的是特征、选择或者 种类等不能定量化的东西, 种类等不能定量化的东西,如乘公交还是自己开车去 上班、考不考研究生等。在这些情况下, 上班、考不考研究生等。在这些情况下,因变量是定 性变量,我们可以用定义虚拟变量的方法来刻画它们。 性变量,我们可以用定义虚拟变量的方法来刻画它们。 这种因变量为虚拟变量的模型被称为 定性选择模型( models) 定性选择模型(Qualitative choice models) 或 定性响应模型( models) 定性响应模型(Qualitative response models)
( ) 10.5
从而得到一个不可能的结果(概率值大于1)。假设 另有一个学生丙的GPA为1.0,家庭收入为5万元,则 其Y的拟合值为 -0.2,表明读研的概率为负数,这也 是一个不可能的结果。
解决此问题的一种方法是,令所有负拟合值都等 于0,所有大于1的拟合值都等于1。但也无法令人十 分满意,因为在现实中很少会有决策前某人读研的 概率就等于1的情况,同样,尽管某些人成绩不是很 好,但他去读研的机会仍会大于0。线性概率模型倾 向于给出过多的极端结果:估计的概率等于0或1。 (3) 另一个问题是扰动项不是正态分布的。事实 上,线性概率模型的扰动项服从二项分布。 (4)此外,线性概率模型存在异方差性。扰动项 的方差是 p(1− p) ,这里 p是因变量等于1的概率, 此概率对于每个观测值不同,因而扰动项方差将不 是常数,导致异方差性。可以使用WLS法,但不是 很有效,并且将改变结果的含义。
其中:
1 Yi = 0
(10.2)
第i个学生拿到学士学位后 三年内去读研 该生三年内未去读研
GPA = 第 个 生 科 均 绩 i 学 本 平 成 i
INCOMEi = 第i个学生家庭年收入(单 位:千美元)
设回归结果如下(所有系数值均在10%水平统计 上显著):
ˆ Yi = −0.7 + 0.4GPA + 0.002INCOMEi ( ) 10.3 i
尽管因变量在这个二元选择模型中只能取两个值: 尽管因变量在这个二元选择模型中只能取两个值: 0或1,可是该学生的的拟合值或预测值为 。我们 或 ,可是该学生的的拟合值或预测值为0.8。 将该拟合值解释为该生决定读研的概率的估计值。因 将该拟合值解释为该生决定读研的概率的估计值。 该生决定读研的可能性或概率的估计值为0.8。 此,该生决定读研的可能性或概率的估计值为 。 需要注意的是,这种概率不是我们能观测到的数字, 需要注意的是,这种概率不是我们能观测到的数字, 能观测的是读研还是不读研的决定。 能观测的是读研还是不读研的决定。 对斜率系数的解释也不同了。在常规回归中,斜 率系数代表的是其他解释变量不变的情况下,该解释 变量的单位变动引起的因变量的变动。而在线性概率 模型中,斜率系数表示其他解释变量不变的情况下, 该解释变量的单位变动引起的因变量等于1的概率的 变动。
CAND1i = β0 + β1INCOMEi + β2 AGEi + β3MALEi + ui ( ) 10.6 其中: 第 投 人 的 1 如果 i个选民 候选 甲 票
CAND i = 1 果 i 民 候 甲 票 0 如 第 个选 不投 选人 的
INCOMEi = 第 个 民 i 选 的家 收入 庭 (单位 千 元 : 美 )
1 jL = ∏P∏(1− P) i i
Y= i 1 Y =0 i
(10.10)
(10.9)式中F的函数形式取决于有关扰动项u的假 设,如果 ui的累积分布是logistic分布,则我们得到 的是logit模型。在这种情况下,累积分布函数为:
exp(zi ) F(zi ) = 1+ exp(zi )
Observations:30 R2 = 0.58 2 Adjusted R = 0.53 Residual Sum of Squares =3.15 F-statistic = 11.87
如表10-2所示,INCOME的斜率估计值为正,且 在1%的水平上显著。年龄和性别不变的情况下,收入 增加1000元,选择候选人甲的概率增加0.0098。 AGE的斜率估计值也在1%的水平上显著。在收入 和性别不变的情况下,年龄增加1岁,选择候选人甲的 概率增加0.016。MALE的斜率系数统计上不显著,因 而没有证据表明样本中男人和女人的选票不同。 我们可以得出如下结论:年老一些、富裕一些的选 民更喜欢投票给候选人甲。 表10-3给出CAND1的拟合值,每个大于等于0.5的 拟合值计入CAND1为1的预测,而小于0.5的拟合值则 计入CAND1为0的预测。
*
P = Pr ob(Yi =1) = Pr ob[ui > −(β0 + ∑β j Xij )] i
j =1
k
=1− F[−(β0 + ∑β j Xij )]
j =1
k
其中F是u的累积分布函数。 如果u的分布是对称的,则 1− F(−z) = F(z) ,我们 可以将上式写成
P = F(β0 + ∑β j Xij ) i
从表10-3可看出,30个观测值中,27个(或90%) 预测正确。选甲的14人中,12人(或85.7%)预测正 确。选乙的16人中,15人(或93.8%)预测正确。 是0.58,表明模型解释了因变量的58%的变动, 这与90%的正确预测比例相比,低了不少。注意表10 R2 -3中有一些拟合值大于1或小于0。这是我们前面指 出的这类模型的缺点之一,这些拟合值是概率的估计 值,而概率永远不可能大于1或小于0。
对每个观测值,我们可根据(10.3)式计算因变量 的拟合值或预测值。在常规OLS回归中,因变量的拟 合值或预测值的含义是,平均而言,我们可以预期的 因变量的值。但在本例的情况下,这种解释就不适用 了。假设学生甲的平均分为3.5,家庭年收入为5万美 元,Y的拟合值为
ˆ Y = −0.7 + 0.4×3.5 + 0.002×50 = 0.8 ( ) 10.4
( ) 10.8
这就是Probit和Logit方法的思路。Probit模型和 Logit模型的区别在于对(10.7)式中扰动项u的分布 的设定,前者设定为正态分布,后者设定为logistic分 布。 (10.7)式与线性概率模型的区别是,这里假设潜 变量的存在。例如,若被观测的虚拟变量是某人买车 还是不买车, i* 将被定义为“买车的欲望或能力”, Y 注意这里的提法是“欲望”和“能力”,因此(10.7) 式中的解释变量是解释这些元素的。 从(10.8)式可看出,Yi 乘上任何正数都不会改 * 变 Y,因此这里习惯上假设 Var(ui) = 1,从而固定 Yi i 的规模。由(10.7)和(10.8)式,我们有
线性概率模型存在的问题
(1)线性概率模型假定自变量与Y=1的概率之间存 在线性关系,而此关系往往不是线性的。 (2)拟合值可能小于0或大于1,而概率值必须位于 0和1的闭区间内。 回到有关读研的例子。假设学生乙的GPA为4.0, 家庭收入为20万美元,则代入(10.3)式,Y的拟合 值为
ˆ Y = −0.7 + 0.4×4.0 + 0.002×200 =1.3
第二节 Probit模型和Logit模型
一.Probit和Logit方法概要 估计二元选择模型的另一类方法假定回归模型为
Yi* = β0 + ∑β j Xij + ui
j =1
k
(10.7)
这里 Y 不可观测,通常称为潜变量(latent i variable)。我们能观测到的是虚拟变量:
*
1 若Y* > 0 i Yi = 其 它 0
正 确预 测的 测值 观 数 正 确预 测观 值的 测 百分 = 比 ×100 观 测值 总数
需要指出的是,这个测度也不是很理想,但预测结 果的好坏,并非定性选择模型唯一关心的事,这类模 型常被用于研究影响人们进行某个决策的因素。让我 们来看一个竞选的例子。假设候选人甲和乙二人竞选 某市市长,我们可以用一个二元选择模型来研究影响 选民决策的因素,数据见表10-1,模型为:
如果只有两个选择,我们可用 和 如果只有两个选择,我们可用0和1 分别表示它 如乘公交为0,自驾车为1, 们,如乘公交为 ,自驾车为 ,这样的模型称为 二元选择模型( 二元选择模型(binary choice Models)。 )。 多于两个选择(如上班方式加上一种骑自车) 多于两个选择(如上班方式加上一种骑自车) 的定性选择模型称为多项选择模型( 的定性选择模型称为多项选择模型(Multinomial choice models)。 )。
(10.1)
这看上去与典型的OLS回归模型并无两样,但区 别是这里Y只取0和1两个值,观测值可以是个人、公 司、国家或任何其他横截面个体所作的决定。解释变 量中可以包括正常变量和虚拟变量。
下面用一个关于是否读研究生的例子来说明如何 解释线性概率模型的结果。模型为:
Yi = β0 + β1GPA + β2INCOMEi + ui i
AGEi = 第i个选民的年龄
1 男性 MALEi = 0 女性
表10-2 两候选人选举线性概率模型回归结果 Dependent variable:CAND1
Variable Constant INCOME AGE MALE Coefficient -0.51 0.0098 0.016 0.0031 Standard error 0.19 0.003 0.0053 0.13 t-Statistic -2.65 3.25 3.08 0.02 p-Value 0.01 0.00 0.00 0.98
