圆内接正五边形(五等分圆周)尺规作图法
画圆的内切正五边形原理

画圆的内切正五边形原理
画圆的内切正五边形的原理如下:
1. 首先,在画布上选择一个点作为圆心,然后画一个与这个圆心垂直的直线,作为正五边形的底边。
2. 根据正五边形的定义,五边形的内角均为108度,因此将底边平分为五等分,得到五个相邻的点。
3. 以圆心为中心,其中一个点为半径,画一个圆弧,该圆弧与底边相交于另一个点。
4. 依次以当前点和圆心为中心,画圆弧与底边相交,共得到五个相邻点。
5. 连接相邻的点,得到内切正五边形的五条边。
6. 删除多余的线段,只保留内切正五边形即可完成。
需要注意的是,画出的图形只是近似地内切于圆的正五边形,因为精确的内切正五边形无法用直尺和圆规画出。
圆的内接正五边形原理讲解

圆的内接正五边形原理讲解圆的内接正五边形原理是指能够被一个圆所内接的正五边形的构造原理。
正五边形是一个具有五个边长相等、五个内角相等且每个内角为108度的多边形。
要理解圆的内接正五边形原理,我们需要了解一些相关的数学知识。
首先,我们来看一下圆与正五边形之间的关系。
一个圆可以由一个中心点和到该中心点的任意一点的距离(即半径)所确定,而正五边形可以由五个相等长度的边所确定。
在一个正五边形中,五个顶点所在的直径线可以通过圆的中心点,并且每个顶点与中心点所形成的角都为72度(360度/5个顶点)。
接下来,我们要明确的是正五边形的特性,即五个边长相等且每个内角为108度。
为了证明这一点,我们可以利用正五边形的对称性和角度和为180度的性质。
我们可以假设边长为1,然后利用三角函数的性质来计算正五边形的各个内角的大小。
通过计算可以得到,每个内角的大小为108度。
基于上述的认识,我们可以开始讲解圆的内接正五边形的构造原理。
首先,在平面上画一个与圆的半径相等的线段OA,其中点O为圆的中心点,点A为正五边形的一个顶点。
然后,以点O为中心,以OA的长度为半径,画一个圆。
我们可以看到,这个圆是与线段OA相切的,因为它们共用了一条边,即OA。
这个圆就被称为内切圆。
接下来,在内切圆的切点B处画一条与线段OA平行的直线BC,直线BC延长线与圆交于点D。
我们可以看到,由于BC是与直径线OA平行的,所以线段OD应该等于线段OB。
因此,我们可以得出三角形OBD是一个等边三角形,即BD=OB=OD。
然后,我们连接线段OA与线段BD,线段OD与线段AB。
这样就构成了一个正五边形OABD。
我们可以通过计算可以得到,五个边长都等于线段OA的长度,即五个边长都等于内切圆的半径。
因此,根据构造的过程和计算的结果,我们可以得出结论:在一个圆中,可以构造一个内接正五边形。
同时,我们还可以得到一个结论:在一个内接正五边形中,五个顶点所在的直径线都可以通过圆的中心点,并且每个顶点与中心点所形成的角都为72度。
正五边形尺规作图方法赏析

正五边形尺规作图方法赏析作者:谢俊峰来源:《数学大世界·上旬刊》2018年第11期尺规作图是起源于古希腊的数学课题。
历史上最先明确提出尺规限制的是希腊天文学家、数学家伊诺皮迪斯。
由于对尺规作图的限制,使得一些貌似简单的几何作图问题无法解决。
最著名的是古希腊最有影响力的四大数学学派之——巧辨学派提出的三大著名尺规作图问题:倍立方问题、化圆为方问题、三等分角,当然,这三个问题都已被证明不可能用尺规作图来解决。
尺规作图中有许多有趣的问题,其中作正多边形就是其中一种。
大家认为这是一个简单的问题,但在操作中我们知道,正四邊形、正五边形、正六边形都比较简单,但到正七边形、正九边形却遇到了很大的困难,最终解决这个问题的是伟大的数学家高斯,他给出了可用尺规作图的正多边形的条件:尺规作图正多边形的边数目必须是2的非负整数次方和不同的费马素数的积。
本文提供正五边形的几种作图方法,供大家赏析。
一、已知圆的半径为r,求作圆的内接正五边形作法1:如图1,作圆O的任意半径OA1,A1B⊥OA1,并使得A1B=1/2OA1,连接BO,以B为圆心,删,为半径作弧截BO于点C,以O为圆心、0C为半径作弧截0A1于点M,以点A1起顺次截取等于0M的弦A1B2,A2B3,…,A10A1,将A2、A4、A6、A8、A10顺次连接,即为圆的内接正五边形。
作法2:如图2,作互相垂直的直径AM,BN,作0N的垂直平分线交ON于点E,以E为圆心、EA为半径作弧交OB于点F,从点A起顺次在圆上截取等于AF的弦,AA1、A1A2、A2A3、A3A4、A4A,顺次连接A、A1、A2、A3、A4、A,即得到正五边形。
作法3:如图3,任作圆O的半径OA,,过O点作OA1的垂线OB交圆O于点B,取OB的中点C,作∠OCA1的角平分线CD交于点D,过D点作DA2⊥OA1交圆O于点A2,从点A2起顺次在圆上截取等于A1A2的弦A2A3、A3A4、A4A5,顺次连接A1、A2. A3、A4.A5、A,即得到正五边形。
正五边形尺规作图的画法及其他

正五边形尺规作图的画法及其他正五边形的画法圆内接正五边形的画法如下:1、作一个圆,设它的圆心为O;2、作圆的两条互相垂直的直径AZ和XY;3、作OY的中点M;4、以点M为圆心,MA为半径作圆,交OX于点N;5、以点A为圆心,AN为半径,在圆上连续截取等弧,使弦AB=BC=CD=DE=AN,则五边形ABCDE即为正五边形。
以上两种图形的作法运用了所求图形边长与已知的线段长度的关系,用构造直角三角形的方法作出与所求图形的边长相等的线段,从而作出整个图形,这是尺规作图中常用的一种方法——等线段法,即用已知图形的线段作出与所求图形边长相等的线段。
正多边形的尺规作图是大家感兴趣的.正三边形很好做;正四边形稍难一点;正六边形也很好做;正五边形就更难一点,但人们也找到了正五边形的直规作图方法.确实,有的困难一些,有的容易一些.正七边形的尺规作图是容易一些,还是困难一些呢?人们很久很久未找到作正七边形的办法,这一事实本身就说明作正七边形不容易;一直未找到这种作法,也使人怀疑:究竟用尺规能否作出正七边形来?数学不容许有这样的判断:至今一直没有人找到正七边形的尺规作图方法来,所以断言它是不能用尺规作出的.人们迅速地解决了正三、四、五、六边形的尺规作图问题,却在正七边形面前止步了:究竟能作不能作,得不出结论来.这个悬案一直悬而未决两千余年.17世纪的费马,就是我们在前面已两次提到了的那个法国业余数学家,他研究了形如Fi (i为右下角标)=22i(底数2指数2的i次幂)+1 的数.费马的一个著名猜想是,当n≥3时,不定方程xn+yn=zn没有正整数解.现在他又猜测Fi都是素数,对于i=0,1,2,3,4时,容易算出来相应的Fi:F0=3,F1=5,F2=17,F3=257,F4=65 537验证一下,这五个数的确是素数.F5=225+1是否素数呢?仅这么一个问题就差不多一百年之后才有了一个结论,伟大的欧拉发现它竟不是素数,因而,伟大的费马这回可是猜错了!F5是两素数之积:F5=641×6 700 417.当然,这一事例多少也说明:判断一个较大的数是否素数也决不是件简单的事,不然,何以需要等近百年?何以需要欧拉这样的人来解决问题?更奇怪的是,不仅F5不是素数,F6,F7也不是素数,F8,F9,F10,F11等还不是素数,甚至,对于F14也能判断它不是素数,但是它的任何真因数还不知道.至今,人们还只知F0,F1,F2,F3,F4这样5个数是素数.由于除此而外还未发现其他素数,于是人们产生了一个与费马的猜想大相径庭的猜想,形如22i+1的素数只有有限个.但对此也未能加以证明.当然,形如Fi=22i+1的素数被称为费马素数.由于素数分解的艰难,不仅对形如Fi=22i+1的数的一般结论很难做出,而且具体分解某个Fi也不是一件简单的事.更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年,一位德国数学家高斯,在他仅20岁左右之时发现,当正多边形的边数是费马素数时是可以尺规作图的,他发现了更一般的结论:正n边形可尺规作图的充分且必要的条件是n=2k(2的k次幂)或2k×p1×p2×…×ps,(1,2…s为右下角标)其中,p1,p2,…,ps是费马素数.正7边形可否尺规作图呢?否!因为7是素数,但不是费马素数.倒是正17边形可尺规作图,高斯最初的一项成就就是作出了正17边形.根据高斯的理论,还有一位德国格丁根大学教授作了正257边形.就这样,一个悬而未决两千余年的古老几何问题得到了圆满的解决,而这一问题解决的过程是如此的蹊跷,它竟与一个没有猜对的猜想相关连.正17边形被用最简单的圆规和直尺作出来了,而正多边形可以换个角度被视为是对圆的等分,那么这也相当于仅用圆规和直尺对圆作了17等分,其图形更觉完美、好看.高斯本人对此也颇为欣赏,由此引导他走上数学道路(他早期曾在语言学与数学之间犹豫过),而且在他逝后的墓碑上就镌刻着一个正17边形图案.高斯把问题是解决得如此彻底,以致有了高斯的定理,我们对于早已知道如何具体作图的正三边形、正五边形,还进而知道了它们为什么能用尺规作图,就因为3和5都是费马素数(3=F0,5=F1);对于很久以来未找到办法来作出的正七边形,乃至于正11边形、正 13边形,现在我们能有把握地说,它们不可能由尺规作图,因为7、11、13都不是费马素数;对于正257边形、正65 537边形,即使我们不知道具体如何作,可是理论上我们已经知道它们是可尺规作图的;此外,为什么正四边形、正六边形可尺规作图呢?因为4=22,因为6= 2· 3而 3=F0.。
1.8 圆内接正五边形
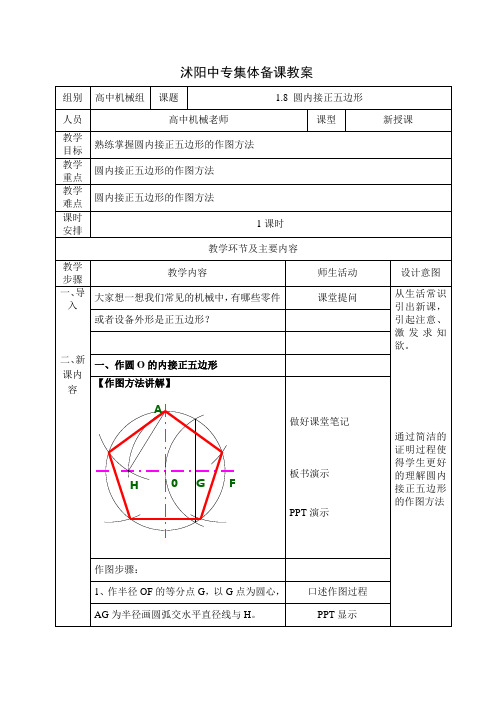
二、课堂练习 三、 总 结 1、作圆 O 的内接正五边形
查漏补缺 学生示范、课堂讲解
【小结】 本节课学习了圆内接正五边形的方 归纳本课所学的内容。 明确本节课 程的重要知 法,希望课后及时巩固所学内容。 识要点。 板 书 设 计 课 后 作 教 学 反 思 1.8 圆内接正五边形 一、作圆 O 的内接正五边形 二、证明过程
2、以 AH 为半径,分圆周为五等分,顺序 连接各等分点即可。 二、证明过程 为什么 AH 就是正五边形的边长呢? 【讲解】 求证:圆内接正五边形的边长 L=AH,已知 Sin36°=(√10-2√5)/4 证明: 设圆 O 的半径为 R 则 L=2RSin36°=R(√10-2√5)/2 ∵在△AOG 中 AG=R√5 在△AOH 中 AH=√AO² +0H² =R(√10-2√5)/2 =L 通过简洁的 证明过程使 得学生更好 的理解圆内 接正五边形 的作法原理 PPT 演示 口述证明过程
二、 一、作圆 O 的内接正五边形 新 课内 【作图方法讲解】 容 A 做好课堂笔记 通过简洁的 证明过程使 得学生更好 的理解圆内 接正五边形 的作图方法
H
0
G
F
板书演示
PPT 演示
作图步骤: 1、作半径 OF 的等分点 G,以 G 点为圆心, AG 为半径画圆弧交水平直径线与 H。 口述作图过程 PPT 显示
练习册习题
沭阳中专集体备课教案
组别 人员 教学 目标 教学 重点 教学 难点 课时 安排 高中机械组 课题 高中机械老师 熟练掌握圆内接正五边形的作图方法 圆内接正五边形的作图方法 圆内接正五边形的作图方法 1 课时 教学环节及主要内容 教学 教学内容 步骤 一、 大家想一想我们常见的机械中, 导 有哪些零件 入 或者设备外形是正五边形? 师生活动 课堂提问 设计意图 从生活常识 引出新课, 引起注意、 激 发 求知 欲。 1.8 圆内接正五边形 课型 新授课
内接正五边形画法原理

内接正五边形画法原理内接正五边形是指一个正五边形的每个顶点都与内切圆的圆心相连,从而形成的一种特殊图形。
它是一个具有很高美学价值和几何特性的图形,其画法原理是通过一系列几何构造来完成的。
本文将详细介绍内接正五边形的画法原理。
我们需要明确内接正五边形的定义。
内接正五边形是指一个正五边形的每个顶点都与内切圆的圆心相连,从而形成的一种特殊图形。
它具有以下特点:1. 五个顶点均位于内切圆上;2. 五个顶点与内切圆圆心相连的线段长度相等;3. 每条边均与相邻两条边成72度的夹角。
接下来,我们来介绍内接正五边形的画法原理。
画内接正五边形的关键是确定内切圆的半径。
假设内切圆的半径为r,我们可以通过一系列几何构造来找到r的值。
我们以正五边形的中心为圆心,画一个半径为r的圆。
然后,我们连接圆的圆心和任意一个顶点,得到一条半径为r的线段。
接着,我们以这条线段为边长,画一个正三角形,将其顶点与圆心相连。
这样,我们就得到了一个以内切圆为外接圆的正三角形。
接下来,我们再次以正三角形的一个顶点为圆心,画一个半径为r 的圆。
然后,我们连接圆的圆心和正三角形的另外两个顶点,得到两条半径为r的线段。
接着,我们以这两条线段为边长,分别画两个正三角形,将它们的顶点与圆心相连。
这样,我们就得到了两个以内切圆为外接圆的正三角形。
重复以上步骤,我们可以得到一个以内切圆为外接圆的正五边形。
在这个过程中,每次都会得到两个新的正三角形,并且内切圆的半径会不断逼近我们所期望的值。
需要注意的是,在实际操作中,我们可以使用各种工具来辅助完成这些几何构造。
例如,我们可以使用直尺来画线段,使用指南针来画圆等。
这样可以更加准确地完成内接正五边形的画法。
总结起来,内接正五边形的画法原理是通过一系列几何构造来确定内切圆的半径,并最终得到一个以内切圆为外接圆的正五边形。
这个过程需要使用几何知识和相关工具,以保证结果的准确性和美观性。
内接正五边形作为一种具有高度对称性和几何美感的图形,广泛应用于艺术、建筑和设计等领域。
内接正五边形画法原理
内接正五边形画法原理内接正五边形是指一个五边形的内接圆的圆心与五边形的顶点连线所形成的五条线段相等。
内接正五边形画法原理是指如何根据已知的五边形边长来构造内接正五边形的方法。
我们需要了解内接正五边形的特性。
由于内接正五边形的五条边相等,所以五边形的边长可以作为内接正五边形的边长。
另外,五边形的内角和为540度,所以内接正五边形的每个内角为108度。
根据内接正五边形的特性,我们可以采用以下方法来构造内接正五边形。
方法一:利用正五边形的对称性画一个正五边形。
可以通过以下步骤来画出正五边形:1. 画一条直线作为五边形的一条边。
2. 在直线的一个端点处作一个等边三角形。
3. 在等边三角形的一条边上作一个等边三角形。
4. 依次类推,画出五边形的其他边。
接下来,利用正五边形的对称性来构造内接正五边形。
具体步骤如下:1. 在正五边形的一个顶点上作一条与边平行的线段。
2. 作一条与这条线段垂直且长度为正五边形边长的线段。
3. 这条线段的终点即为内接正五边形的一个顶点。
4. 依次类推,可得到内接正五边形的其他顶点。
方法二:利用正五边形的内切圆另一种构造内接正五边形的方法是利用正五边形的内切圆。
具体步骤如下:1. 画一个正五边形。
2. 作正五边形的内切圆,即将圆心放在正五边形的内角平分线上。
3. 这个内切圆的半径即为内接正五边形的边长。
4. 连接内切圆的圆心与正五边形的顶点,即可得到内接正五边形。
无论是利用正五边形的对称性还是利用内切圆,都可以很容易地构造出内接正五边形。
这些方法都基于内接正五边形的特性,通过合理的构造步骤来实现。
内接正五边形在几何学中有着重要的应用,它具有很多有趣的性质和特点。
例如,内接正五边形的对角线之间的夹角为72度,内接正五边形的面积可以通过边长来计算,公式为(5/4) * a^2 * tan(π/5),其中a为边长。
总结起来,内接正五边形的画法原理是根据内接正五边形的特性,通过构造合适的线段或圆来实现。
尺规作图正五边形
尺规作图正五边形
[正五边形的画法]
圆内接正五边形的画法如下:
①以O为圆心,定长R为半径画圆,并作互相垂直的直径MN和 AP.
②②平分半径ON,得OK=KN.
③③以 K为圆心,KA为半径画弧与 OM交于 H, AH即为正五边形的
边长.
④④以AH为弦长,在圆周上截得A,B,C,D,E各点,顺次连接这些点即
得正五边形.
⑤已知边长作正五边形的近似画法如下:
⑥①作线段AB等于定长l,并分别以A,B为圆心,已知长l为半径画
弧与AB的中垂线交于K.
⑦②以K为圆心,取AB的2/3长度为半径向外侧取C点,使CK=2/3AB
⑧③以 C为圆心,已知边长 AB为半径画弧,分别与前两弧相交于
M,N.
⑨④顺次连接A,B,N,C,M各点即近似作得所要求的正五边形.
在圆内作一个正三角形
先画个圆O。
半径为R
在圆上取任意一点P圆心。
半径仍为R做弧。
与圆O相交与AB两点。
AB是正三角形的两个顶点了。
再以A为圆心,半径仍为R做弧。
与圆O又有两个交点。
其中一个肯定为第1次做弧的圆心P。
还有个设为Q
以Q为圆心。
半径为R作弧。
与圆O有两个交点。
一个为A,另一个为C
则三角形ABC为正三角形。
正五边形尺规作图的画法及其他
正五边形尺规作图的画法及其他正五边形的画法圆内接正五边形的画法如下:1、作一个圆,设它的圆心为O;2、作圆的两条互相垂直的直径AZ和XY;3、作OY的中点M;4、以点M为圆心,MA为半径作圆,交OX于点N;5、以点A为圆心,AN为半径,在圆上连续截取等弧,使弦AB=BC=CD=DE=AN,则五边形ABCDE即为正五边形。
以上两种图形的作法运用了所求图形边长与已知的线段长度的关系,用构造直角三角形的方法作出与所求图形的边长相等的线段,从而作出整个图形,这是尺规作图中常用的一种方法——等线段法,即用已知图形的线段作出与所求图形边长相等的线段。
正多边形的尺规作图是大家感兴趣的.正三边形很好做;正四边形稍难一点;正六边形也很好做;正五边形就更难一点,但人们也找到了正五边形的直规作图方法.确实,有的困难一些,有的容易一些.正七边形的尺规作图是容易一些,还是困难一些呢?人们很久很久未找到作正七边形的办法,这一事实本身就说明作正七边形不容易;一直未找到这种作法,也使人怀疑:究竟用尺规能否作出正七边形来?数学不容许有这样的判断:至今一直没有人找到正七边形的尺规作图方法来,所以断言它是不能用尺规作出的.人们迅速地解决了正三、四、五、六边形的尺规作图问题,却在正七边形面前止步了:究竟能作不能作,得不出结论来.这个悬案一直悬而未决两千余年.17世纪的费马,就是我们在前面已两次提到了的那个法国业余数学家,他研究了形如Fi (i为右下角标)=22i(底数2指数2的i次幂)+1 的数.费马的一个著名猜想是,当n≥3时,不定方程xn+yn=zn没有正整数解.现在他又猜测Fi都是素数,对于i=0,1,2,3,4时,容易算出来相应的Fi:F0=3,F1=5,F2=17,F3=257,F4=65 537验证一下,这五个数的确是素数.F5=225+1是否素数呢?仅这么一个问题就差不多一百年之后才有了一个结论,伟大的欧拉发现它竟不是素数,因而,伟大的费马这回可是猜错了!F5是两素数之积:F5=641×6 700 417.当然,这一事例多少也说明:判断一个较大的数是否素数也决不是件简单的事,不然,何以需要等近百年?何以需要欧拉这样的人来解决问题?更奇怪的是,不仅F5不是素数,F6,F7也不是素数,F8,F9,F10,F11等还不是素数,甚至,对于F14也能判断它不是素数,但是它的任何真因数还不知道.至今,人们还只知F0,F1,F2,F3,F4这样5个数是素数.由于除此而外还未发现其他素数,于是人们产生了一个与费马的猜想大相径庭的猜想,形如22i+1的素数只有有限个.但对此也未能加以证明.当然,形如Fi=22i+1的素数被称为费马素数.由于素数分解的艰难,不仅对形如Fi=22i+1的数的一般结论很难做出,而且具体分解某个Fi也不是一件简单的事.更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年,一位德国数学家高斯,在他仅20岁左右之时发现,当正多边形的边数是费马素数时是可以尺规作图的,他发现了更一般的结论:正n边形可尺规作图的充分且必要的条件是n=2k(2的k次幂)或2k×p1×p2×…×ps,(1,2…s为右下角标)其中,p1,p2,…,ps是费马素数.正7边形可否尺规作图呢?否!因为7是素数,但不是费马素数.倒是正17边形可尺规作图,高斯最初的一项成就就是作出了正17边形.根据高斯的理论,还有一位德国格丁根大学教授作了正257边形.就这样,一个悬而未决两千余年的古老几何问题得到了圆满的解决,而这一问题解决的过程是如此的蹊跷,它竟与一个没有猜对的猜想相关连.正17边形被用最简单的圆规和直尺作出来了,而正多边形可以换个角度被视为是对圆的等分,那么这也相当于仅用圆规和直尺对圆作了17等分,其图形更觉完美、好看.高斯本人对此也颇为欣赏,由此引导他走上数学道路(他早期曾在语言学与数学之间犹豫过),而且在他逝后的墓碑上就镌刻着一个正17边形图案.高斯把问题是解决得如此彻底,以致有了高斯的定理,我们对于早已知道如何具体作图的正三边形、正五边形,还进而知道了它们为什么能用尺规作图,就因为3和5都是费马素数(3=F0,5=F1);对于很久以来未找到办法来作出的正七边形,乃至于正11边形、正 13边形,现在我们能有把握地说,它们不可能由尺规作图,因为7、11、13都不是费马素数;对于正257边形、正65 537边形,即使我们不知道具体如何作,可是理论上我们已经知道它们是可尺规作图的;此外,为什么正四边形、正六边形可尺规作图呢?因为4=22,因为6= 2· 3而 3=F0.。
正五边形的常见绘制方法
正五边形的常见绘制方法作者:张静来源:《卷宗》2015年第08期摘要:本文主要介绍正五边形的常见绘制方法,即已知正五边形的外接圆直径、内切圆直径、边长等不同条件时的正五边形的绘制方法。
关键词:正五边形;内切圆;外接圆;边长由于正五边形具有一定的实用性和趣味性,在高等职业教育中,常把正五边形的绘制作为一个教学内容,来训练学生的几何图形绘制能力和综合制作能力。
综观各种教材及实际生产中关于正五边形的绘制,可分为下述三种方法:1 已知正五边形外接圆直径来绘制正五边形已知正五边形的外接圆直径,来绘制五边形,实质上就是要根据作图法来求出该正五边形的边长,求出边长后,在已知外接圆周上按该边长来进行截取,会得到圆周上的五等分点,依次连接各等分点,即为所求五边形,该方法无论作图过程如何认真、精确,最后都会存在一定的误差,改方法是一种近似的绘图方法。
已知正五边形外接圆的直径Ф,作圆内接正五边形的方法和步骤如图1所示:1、已知直径为Ф的圆及圆上的点P、N,作ON的中点M,如图1(1)所示;2、以M为圆心,MA为半径作弧交OP于K,AK即为圆内接正五边形的边长,如图1(2)所示;3、以AK为边长,自A点起,五等分圆周得B、C、D、E点,依次连接各点,即得圆内接正五边形ABCDE,如图1(3)所示。
2 已知正五边形内切圆直径来绘制正五边形该方法主要作图原理为:正五边形各边的中点均是正五边形与其内切圆的切点,并且这五个切点还是其内切圆的五等分点。
已知正五边形内切圆的直径Ф,作正五边形的方法和步骤如图2所示:1、作正五边形内切圆,并对该圆等分,得五等分点A、B、C、D、E,并将其与圆心O 连接,如图2(1)所示;2、过A、B、C、D、E各点分别作OA、OB、OC、OD、OE的垂线,并两两相交得1、2、3、4、5五点,如图2(2)所示;3、依次连接1、2、3、4、5各点,并描深得五边形,如图2(3)所示。
3 已知边长作正五边形的近似画法已知边长作正五边形的画法及步骤如图3所示:1、作线段AB,其长等于正五边形长a,如图3(1)所示;2、分别以A,B为圆心,已知长a为半径画弧与AB的中垂线交于M,如图3(2)所示;3、把AB进行三等分,取AB的2/3长度,沿着中垂线由M点向上取N点,使MN=2/3AB,如图3(3)所示;4、以点N为圆心,已知边长AB为半径画弧,分别与前两弧相交于E、F,如图3(4)所示;5、顺次连接A,B,F,N,E各点即近似作得所要求的正五边形,如图3(5)所示;综上所述,当正五边形的已知条件不同时,其绘制方法也不同,所以,绘制正五边形时,应先对其给定的已知条件进行分析,然后再绘制正五边形。
