9.2刚体惯性力系的简化
刚体惯性力系的简化

代入式(a)得 再解式(b)、式(c)有
a g 3
Ff
P 2
P g
g 3
P 6
FN P cos
3P 2
P
f Ff 6 3 0.192
FN
3P 9
2
(b) (c)
例13-7 均质杆 AB 重 P,B 点放在地面上,A 点与轮铰接,轮在平面上纯
滚动,轮心做匀速直线运动,速度为 v,如图 13-11(a)所示。试 求在图示位置(A 位于最高点)时,AB 杆在 A,B 两点的受力情况 (B 与地面无摩擦)。
在工程实际中,刚体绕定轴转动有几种特殊情况。
(1)转轴过质心。此时 aC 0 ,FI 0 ,在 0 的情况下,惯性力系简 化为一个力偶。
(2)刚体做匀速转动,此时 0 ,在转轴不过质心的情况下,惯性力 系简化为一个合力。
(3)转轴过质心,刚体做匀速转动,aC 0 , 0 ,则 FI 0 ,MIO 0 。
(a)
(b) 图13-11
(c)
解 (1)取AB杆为研究对象。
(2)受力分析。AB 杆上作用的主动力为重力 P,A 点有两个约束力 FAx 和 FAy , B 点有法向约束力 FBN ,如图 13-11(b)所示。
(3)运动分析,加惯性力。由已知条件,AB 杆为瞬时平动,即 AB 0 ,对 AB
FI FIi (miai ) aC mi 设刚体质量为 M mi ,则
FI MaC (13-8)
于是得结论:平动刚体的惯性力系可以简化为通过质心 的合力,其大小等于刚体的质量与加速度的乘积,合力的 方向与加速度方向相反。
图13-5
刚体绕定轴转动
如果刚体有对称平面S,并且该平面与转轴z垂直,则惯性力系简化 为在对称平面内的平面力系。再将此平面力系向转轴与对称平面的交 点O简化,如图13-6所示。
理论力学 第十三章达朗贝尔原理

设有一质点系由n个质点组成 第i个质点Mi,质量mi,受主动力 F, i 约束反力 FNi 作用,加速度为 ai ,对每一个质点,有: G G Fi mi ai Fi FNi Fi 0 (i 1, 2,, n)
表示为力系形式: G G G (F1,, Fi ,, Fn , FN1,, FNi ,, FNn , F 1 ,, F i ,, F n )0
G rC为刚体质心相对于质心 的矢径, rC 0MC 0
结论:刚体作平动时,惯性力系对质心C的主矩为零。
19
mi ri aC mrC aC
§13–2 刚体惯性力系的简化
三、刚体作定轴转动
讨论具有质量对称平面且转轴垂直于质量对称平面 的情况。(刚体的空间惯性力系投影在对称平面内 的平面力系,再将此平面力系向O点简化,O点为质 量对称平面与转轴Z的交点。) 空间惯性力系 平面惯性力系 (质量对称面) 直线 i : 平动, 过Mi点,惯性力系 G 为
将质点系受力按内力、外力划分:
(内力是大小相等,方向相反成 对出现,所以内力主矢和对任意点 的主矩分别恒为零)
e e e G G G (F1 ,, Fi ,, Fn , F1 ,, Fi ,, Fn ) 0 e G Fi Fi 0 e G M O ( Fi ) M O ( Fi ) 0
1
第十三章
达朗贝尔原理
§13–1 达朗贝尔原理 §13–2 刚体惯性力系的简化
§13–3 绕定轴转动刚体的动约束力
静平衡和动平衡的概念
2
第十三章
达朗贝尔原理
法国科学家达朗贝尔(J.le Rond d’Alembert)将适 用于自由质点的牛顿定律(第二定律)推广至受约束质 点,并于1743年提出了受约束质点动力学问题的一个原 理—达朗贝尔原理。 达朗贝尔原理为非自由质点系动力学的发展奠定了 基础。该原理提出一百多年后,后人引入了惯性力的概 念,并应用达朗贝尔原理中包含的用静力学中研究平衡 的方法研究动力学中不平衡问题的思想,将这一原理发 展成求解非自由质点系动力学问题的普遍而有效的方法, 称为动静法。 由于动静法简单有效,易于掌握,因此在工程技 术中得到了广泛应用。
理论力学第十一章 达朗贝尔原理(动静法)

讨论:1)脱离角α与滚筒的角速度和滚筒半径有关,而与钢球质量无关。
2)
筒壁。此时转筒
的转速称为临界转速,对球磨机而言,要求n小于nL,否则球磨机就不能工作。
§11-2 刚体惯性力系的简化
刚体平移时惯性力系的简化
当刚体平移时,任一瞬时体内各点的加速度相等。若记某瞬 时刚体质心加速度为aC,则该瞬时体内任一质量为m的质点 的加速度ai=aC,虚加在该点上的惯性力Fgi=-miai=-miaC 。 刚体内每一点都加上相应的惯性力,由静力学知,该空间平 行力系可简化为过质心的合力,即
式中,Fgτ=-maτ,称为切向惯性力 Fgn=-man称为法向惯性力(也称离心力)
负号表示它们分别与切向加速度和法向加速度的方向相反。
§11-1 惯性力与质点的达朗贝尔原理
质点系的动静法
对由n个质点组成的非自由质点系,设其中任一质点的质量 为mi,某瞬时加速度为ai,作用其上的主动力F,约束反力 Fni,假想在该质点上加上惯性力Fgi=-mai,由质点达朗贝 尔原理,则
=- maC
该力偶的力偶矩等于惯性力系对刚体惯性力系的简化
结论 当刚体有质量对称面,且绕垂直于质量对称面的定轴 转动时,惯性力系可以简化为对称面内的一个力和一个力偶。 该力等于刚体的质量与质心加速度的乘积,方向与质心加速 度方向相反,且力的作用线通过转轴;
该力偶的力偶矩等于刚体对转轴的转动惯量与角加速度的乘 积,其转向与角加速度转向相反。惯性力系向点O简化的结 果如图b)所示。
Fg=-m a
质点的达朗伯原理:质点在运动的每一瞬时,作用 于质点上的主动力、约束反力与假想地在质点上 的惯性力,在形式上构成一平衡力系。
§11-1 惯性力与质点的达朗贝尔原理
知识资料理论力学(十四)(新版)(1)

五、达朗伯原理达朗伯原理是一种解决非自由质点系动力知识题的普遍主意。
这种主意将质点系的惯性力虚加在质点系上,使动力知识题可以应用静力学写平衡方程的主意来求解,故称为动静法,动静法在工程技术中得到广泛的应用。
(一)惯性力当质点受到其他物体的作用而改变其本来运动状态时,因为质点的惯性产生对施力物体的反作使劲,称为质点的惯性力。
惯性力的大小等于质点的质量与其加速度的乘积,方向与加速度的方向相反,并作用在施力物体上。
惯性力的表达式为(二)达朗伯原理在非自由质点M运动中的每一瞬时,作用于质点的主动力F、约束反力N和该质点的惯性力FI构成一假想的平衡力系。
这就是质点达朗伯原理,其表达式为在非自由质点系运动中的每一瞬时,作用于质点系内每一质点的主动力Fi、约束反力N,和该质点的惯性力FiI构成一假想的平衡力系。
这就是质点系达朗伯原理。
即(三)刚体运动时惯性力系的简化对刚体动力知识题,可以将刚体上每个质点惯性力组成惯性力系,使劲系简化的主意,得出简化结果。
这些简化结果与刚体的运动形式有关。
详细结果见表4-3-9。
(四)动静法按照达朗伯原理,在质点或质点系所受的主动力、约束反力以外,假想地加上惯性力或惯第1 页/共7 页性力系的简化结果,则可用静力学建立平衡方程的主意求解动力知识题,这种求解动力知识题的主意称为动静法。
必须指出,动静法只是解决动力知识题的一种主意,它并不改变动力知识题的性质,因为惯性力并不作用在质点或质点系上,质点或质点系也不处于平衡状态。
动静法中“平衡”只是形式上的平衡,并没有实际意义。
应用动静法列出的平衡方程,实质上就是运动微分方程。
(五)例题[例4—3—13] 长方形匀质薄板重W,以两根等长的软绳支持如图4—3—37所示。
设薄板在图示位无初速地开始运动,图中α=30°。
求此时绳子中的拉力。
[解](1)对象以平板的为研究对象。
(2)受力分析运动开始时板受重力w、软绳约束反力T1、T2。
河南科技大学土木工程学院2020年考研专业课初试大纲

河南科技大学土木工程学院2020年硕士研究生招生自命题考试科目考试大纲考试科目参考书考试范围801材料力学《材料力学》张淑芬主编,中国建筑工业出版社,2014.03杆件变形的基本形式;拉伸、压缩与剪切的强度条件及变形计算;圆轴扭转的应力、强度、变形的计算;受弯杆件剪力和弯矩的计算方法,掌握绘制剪力图和弯矩图的方法;地求弯曲正应力和弯曲强度的计算,弯曲切应力的求解方法;用积分法和叠加法求解弯曲变形问题,静不定梁的概念及求法;二向应力状态的解析法和图解法,四种强度理论;组合变形的分析方法,求解弯曲与拉伸或压缩的强度计算和扭转与弯曲的强度计算;压杆稳定的概念,正确求解压杆的稳定问题;掌握动静法的方法,正确求解冲击时的应力和变形。
814流体力学《流体力学》张也影主编,第二版,高等教育出版社,2010.12.流体质点与连续介质概念,流体的密度、比体积和相对密度,流体的压缩性和膨胀性,流体的粘性,流体的表面张力与汽化压强;流体静力学,平衡流体上的作用力,流体平衡的微分方程式,重力场中的平衡流体,静压强的计算与测量,平衡流体对壁面的作用力,液体的相对平衡;流体动力学基础,描述流体运动的两种方法,流体运动中的几个基本概念,连续方程,流体微元的运动分析,实际流体的运动微分方程(纳维-斯托克斯方程式),伯努利方程式及其应用,动量方程式及其应用,动量矩方程式;相似和量纲分析,相似原理,Pi定理和量纲分析的应用;管中流动,雷诺实验,圆管中的层流,圆管中的湍流,管路中的沿程阻力,管路中的局部阻力,管路计算;孔口出流,薄壁孔口出流,厚壁孔口出流,孔口及机械中的气穴现象。
815理论力学《理论力学》张淑芬主编,第3版,中国建筑工业出版社,2019, 9静力学公理和物体的受力分析;平面汇交力系、平面力偶系、平面任意力系平衡条件与分析方法;空间力系的平衡条件及分析方法;滑动摩擦。
摩擦角和自锁现象;点的运动学;刚体的基本运动;点的速度合成定理。
922147-理论力学之动力学-第四章2动反力
M Ix J xz J yz 2 M Iy J yz J xz 2
2xc yc 0 xc 2 yc 0
J xz 2 J yz 0 2 J xz J yz 0
FI x
M Iz J z
附加动反力为零或动平衡的充分必要条件:
MIo
y
xc yc 0 Jxz J yz 0 即转轴是中心惯量主轴。
再向A点简化。
18
思考题:当绳A剪断后的瞬时,绳B的拉力如何变化
o1
o2
A
B
C mg
均质杆
A:增加
B:减小
C:不变
19
例:矩形均质板的质量为m,静止放在水平地面上,在其上作 用有一水平推力P,求: 板不会翻倒,h 应满足的条件。
已知:l, L, f fs
l
P
h
mg L
FA
x FN
1、P fsmg 静力学问题
非动平衡动静法动静法刚体惯性力系的简化刚体惯性力系的简化平移刚体平移刚体平面运动刚体平面运动刚体ic定轴转动刚体定轴转动刚体定轴转动刚体轴承动反力定轴转动刚体轴承动反力惯性积惯量主轴中心惯量主轴惯量主轴判据附加动反力为零的充分必要条件静平衡与动平衡18思考题
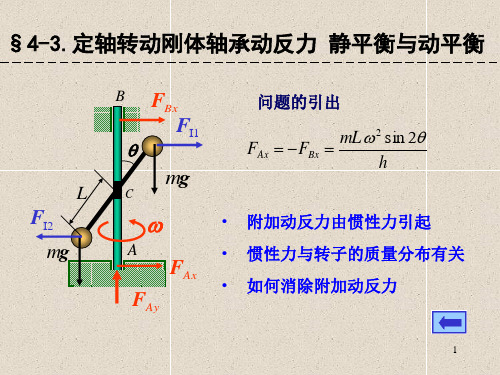
§4-3.定轴转动刚体轴承动反力 静平衡与动平衡
a
a
A : FA FB B : FA FB C : FA FB
27
FIx m( 2 xc yc ) FIy m(xc 2 yc )
xc , yc
质心坐标
FI
FIz 0 x
MIo
y
M Ix J xz J yz 2 M Iy J yz J xz 2 M Iz J z
J xz mi xi zi J yz mi yi zi
理论力学大朗贝尔原理

r arccos( ) g
2
Theoretical Mechanics
返回首页
16.1 达朗贝尔原理
16.1.2 质点系的达朗贝尔原理
设非自由质点系由 n 个质点组成,其中第 i 个 质点的质量为 mi,其加速度为ai ,作用在此质点上 的外力的合力为 Fie,内力的合力为 Fi i。在该质点上 假想地加上惯性力 FIi mi ai ,则由质点的达朗伯 原理,有 Fie Fii FIi 0 (i 1,2, , n)
τ Ii
FIiτ
Mi C
故
M IO I O
FOy=mg
附加动约束力为
FDx
Theoretical Mechanics
7 lm 2 24
FOx
5 lm 2 24
返回首页
16.1 达朗贝尔原理 例15-3 图中飞轮的质量为 m ,平均 半径为R,以匀角速度 绕其中心轴 转动。设轮缘较薄,质量均匀分布, 轮辐的质量忽略不计。若不考虑重力 的影响,求轮缘各横截面的张力。
刚体惯性力系的简化
n Ii
该惯性力系对转轴O的主矩为
M IO M O (F ) M O (F )
F 通过O点,有 M O (F ) 0 ,所以
n Ii
F F
2
n IR
a ri
n i
τ aC
n Ii
τ IR
O M IO n aC
M IO MO (F ) (mi ri )ri (mi ri )
i i i
Fiz FNiz FIiz Fz 0
理论力学-达朗贝尔原理

第五章 达朗贝尔原理
§ 5-2 惯性力系的简化
惯性力系的简化 刚体常见运动情况下
惯性力的主矢和主矩
第五章 达朗贝尔原理
§ 5-2 惯性力系的简化
一、 惯性力系的简化
对于作任意运动的质点系,把实际所受的力和虚加惯性力各自向
● 对转轴的主矩
Mz* Jz
具有质量对称平面的刚体绕垂直 于质量对称平面的固定轴转动时,惯 性力系向固定轴简化的结果,得到合 力偶的力偶矩即为惯性力系的主矩, 其大小等于刚体对转动轴的转动惯量 与角加速度的乘积,方向与角加速度 方向相反。
z
M*z
F
* n
a
t C
O
y
C a
n C
x
F
* t
第五章 达朗贝尔原理
具有质量对称平面的刚体作平面运动,并且运动平面与
质量对称平面互相平行。这种情形下,惯性力系向质心简化
的结果得到一个合力和一个合力偶,二者都位于质量对称平
面内。 ● 主矢
M*C F*
合力的矢量即为惯性力系的 主矢,其大小等于刚体质量与质 心加速度大小的乘积,方向与质 心加速度方向相反。
F* maC
C
ri
例题 5-1
由式(1)和(2)解得
FNA
m ( gc ah ) bc
m ( gb ah ) FNB b c
第五章 达朗贝尔原理
F* C a
h
FB
mg
Bc
b
A
FNB
FNA
§5-3 动静法应用举例
无ABS系统时,刹车会产生侧滑现象
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
刚体定轴转动
刚体有质量对称面,且转轴与对称面垂直。
FIi miai mi (ai ain ) 向转轴O点简化
主矢 FIR miai maC
FIR FInR
主矩 M IO MO (FIi )
[MO (FIi ) MO (FIni )] MO (FIi )
miai ri mi ri2
IC JC
结论:刚体在与质量对称面平行的平面内运动时,惯性力系可以简化 为对称面内的一个力和一个力偶。该力等于maC,方向与aC反
向,作用在质心上;力偶矩等于JC,转向与 相反。
例 设均质齿轮A与一大齿轮内啮合,齿轮A的质量为m,半径为r,
OA杆长为l。若OA杆以角速度、角加速度转动,转向如图。在图ห้องสมุดไป่ตู้
FIi miai mi (aC aiC ainC ) 向质心C点简化
主矢 FIR miai maC
主矩 M IC MC (FIi )
riC C
Mi ainC
MIC
aiC FIR
[MC (FIC ) MC (FIiC ) MC (FIniC )] MC (FIiC ) mi aiC riC
刚体惯性力系的简化
惯性力系的主矢和主矩
质点的惯性力 FI = -ma 质点系的惯性力系 FIi miai
(i 1, 2, 3 , n)
主矢 FIR FIi miai maC
惯性力系的主矢与运动形式无关,与简化中心无关。
主矩
M IO MO (FIi ) ri miai )
惯性力系的主矩与运动形式有关,与简化中心有关。
A
l
r
A
MIO O
FInR FIR
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
小结
•惯性力系的主矢与刚体的运动形式无关。 •惯性力系的主矩与刚体的运动形式有关。 向质心C点简化
平行移动 FIR miai maC IC 0
定轴转动 FIR miai maC IC JC
角加速度为,计算杆上惯性力系向O点和质心C简化的结果。
O
C
A
解:运动分析 向转轴O点简化
aC
l 2
4 2
FIR
maC
ml 2
4 2
MIO
FIR O
A
M IO
JO
1 ml2
3
O
FIR
C
MIC
A
向质心C点简化
FIR
maC
ml 2
4 2
M IC
JC
1 ml2
12
刚体平面运动
刚体有质量对称面,且此平面与刚体运动平面平行。
IC JC
结论:刚体绕与对称面垂直的定轴转动时,惯性力系可以简化为对称 面内的一个力和一个力偶。该力等于maC,方向与aC方向相反,
作用在轴(质心)上;该力偶的矩等于JO (JC),转向与 相反。
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
例 图示均质杆OA质量为m,长为l,绕O点作定轴转动,角速度为,
IO JO
FIR O
MIO
FIR
FInR
ri C
Mi ain
FIi
ai
FIni
刚体定轴转动
FIR O
MIO
刚体有质量对称面,且转轴与对称面垂直。
向质心C点简化
主矢
FIR FIR maC
FIR FInR
aC
MIC
C
主矩 M IC M IO MC (FIR )
FIR
M IO MC (FIR ) Jz FIR rC (Jz mrC2 )
平面运动 FIR miai maC IC JC
示位置,计算齿轮A的惯性力系向O点简化的结果。
FIR
A A
FInR
解:运动分析 向质心A点简化
aA l
aAn l2
O
a
n A
aA MIA
FIR ml FInR ml2
M IA
J A A
1 mr2 l
2
r
mlr
2
向O点简化
FIR ml FInR ml2
M IO
M IA
FIR
l
mlr
2
ml 2
刚体平行移动 FIi miai miaC
主矢 FIR miai maC
FI2 FIR FIn
m2 FI1 m1 a1 a2 C aC
mn an
主矩
MIO MO (FIi ) ri miaC
miri aC mrC aC
当简化中心为质心C时,MIC = 0
结论:平动刚体的惯性力系可以简化为通过质心的合力,其大小 等于刚体的质量与加速度的乘积,方向与加速度方向相反。
